第四章 平行四边形基础巩固训练(含解析)
文档属性
| 名称 | 第四章 平行四边形基础巩固训练(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-22 12:11:10 | ||
图片预览




文档简介
初中数学浙教版八年级下册第四章 平行四边形 基础巩固训练
一、单选题(本大题共10小题,每小题3分,共30分。)
1. 下面列图案中既是轴对称图形又是中心对称图形的是(?? )
A.????????????????B.????????????????C.????????????????D.?
2. 从八边形的一个顶点引对角线,最多把它分割成三角形的个数为(?? )
A.?5???????????????????????????????????????????B.?6???????????????????????????????????????????C.?7???????????????????????????????????????????D.?8
3. 一个多边形内角和是720?,则这个多边形的对角线条数为(??? )
A.?3???????????????????????????????????????????B.?6???????????????????????????????????????????C.?9???????????????????????????????????????????D.?12
4. 下列说法中,正确的个数有:( ??)
①同旁内角互补;②直线外一点与直线上各点连接的所有线段中,垂线段最短;③从直线外一点到这条直线的垂线段的长度,叫做点到直线的距离;④平行线间的距离处处相等.
A.?1个???????????????????????????????????????B.?2个???????????????????????????????????????C.?3个???????????????????????????????????????D.?4个
5. 在平行四边形 ABCD 中,若 ∠A=2∠B ,则 ∠D 的度数是(? )
A.?50°???????????????????????????????????????B.?60°???????????????????????????????????????C.?70°???????????????????????????????????????D.?80°
6. 如图,在 ?ABCD 中, AC 、 BD 相交于点O, AB⊥AC ,若 AB=4 , AC=6 ,则 ΔCOD 的周长是(?? )
A.?8?????????????????????????????????????????B.?10?????????????????????????????????????????C.?12?????????????????????????????????????????D.?16
7. 能判定四边形ABCD是平行四边形的是(??? )
A.?AB∥CD,AB=CD???????????B.?AB=BC,AD=CD???????????C.?AC=BD,AB=CD???????????D.?AB∥CD,AD=CB
8. 如图,在平行四边形ABCD中,对角线AC,BD交于点O,E是BC边上的中点,若 OE=2,AD=5 ,则平行四边形ABCD的周长为(? )?
?
A.?9?????????????????????????????????????????B.?16?????????????????????????????????????????C.?18?????????????????????????????????????????D.?20
9. 用反证法证明命题“在四边形中至少有一个内角不大于90°”时,首先应假设(?? )
A.?每个内角都小于90°
B.?每个内角都大于90°
C.?没有一个内角大于90°
D.?每个内角都等于90°
10. 如图 ∠1,∠2,∠3 是正五边形 ABCDE 的三个外角,若 ∠A+∠B=230°, 则 ∠1+∠2+∠3 =(??? )
A.?140°?????????????????????????????????B.?180°?????????????????????????????????C.?230°?????????????????????????????????D.?320°
二、填空题(本大题共6小题,每小题4分,共24分。)
11. 若一个多边形的内角和与外角和之和是1800°,则此多边形是________边形.
12. 如图,直线AE∥BD,点C在BD上,若AE=4,BD=8,△ABD的面积为16,则 △ACE 的面积为________.
13. 在①平行四边形;②矩形;③菱形;④正方形;⑤等腰梯形这五种图形中,既是轴对称图形又是中心对称图形的是________(只填序号).
14. 如图,在平行四边形 ABCD 中, E,F 两点均在对角线 AC 上.要使四边形 BEDF 为平行四边形,在不添加辅助线的情况下,需要增加的一个条件是________(写出一个即可).
?
15. 如图,AD、BE是△ABC的两条中线,△EDC的面积是2,则△ABD的面积是________.
16. 各顶点都在方格纸的格点(横竖格子线的交错点)上的多边形称为格点多边形,它的面积S可用公式 S=a+12b-1 (a是多边形内的格点数,b是多边形边界上的格点数)计算,这个公式称为“皮克(Pick)定理”.如图给出了一个格点五边形,则该五边形的面积 S= ________.
三、解答题(本大题共8小题,共66分。)
17. (本小题 6分 ) 一个多边形除了一个内角a外,其余内角的和为2680°,求这个多边形的边数和这个内角a的度数.
18. (本小题 6分 ) 如图,在 ?ABCD 中,∠ABC的平分线BE交AD于点E,测得∠AEB=27°,求∠D的度数.
19. ( 本小题6分 )△ABC 的中线BD,CE相交于O,F,G分别是BO,CO的中点,求证: EF//DG ,且 EF=DG .
20. ( 本小题8分 ) 在不等边△ABC中,A是最小角,求证:A<60°.
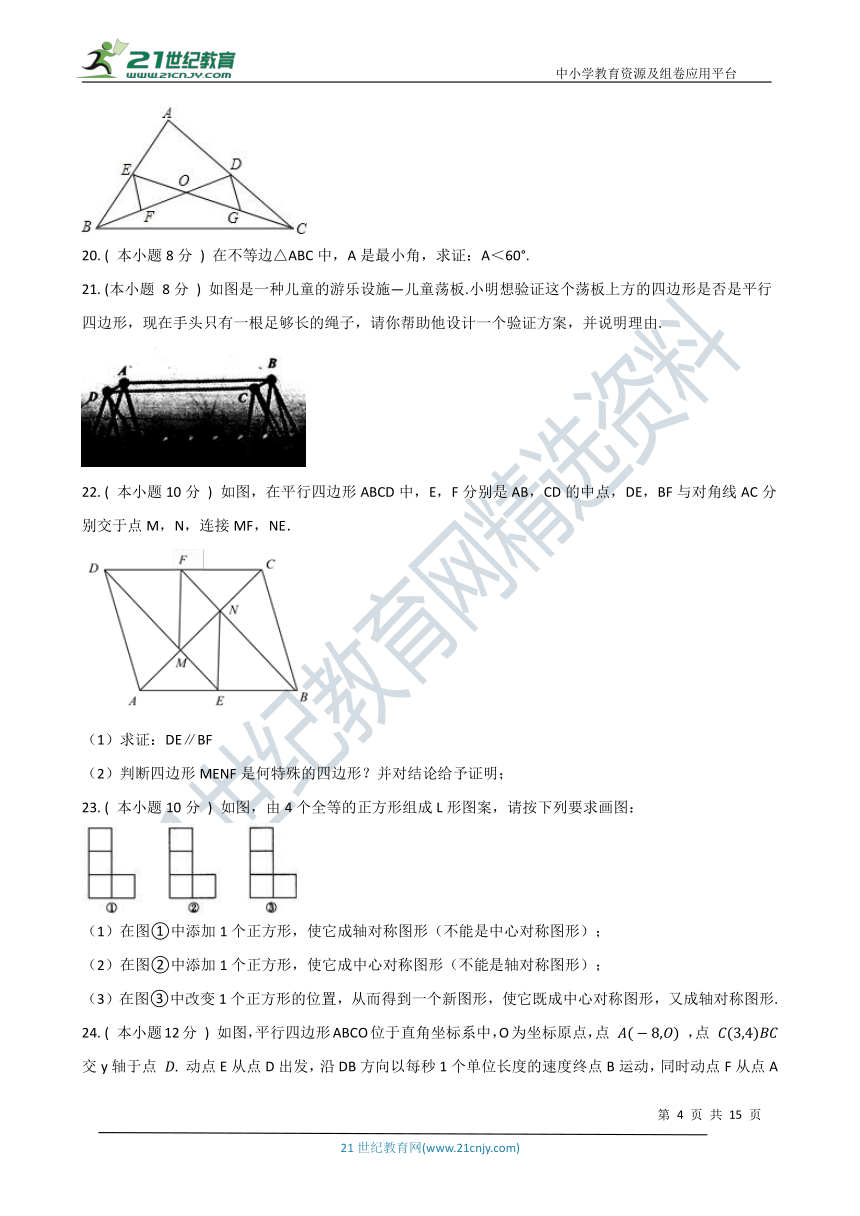
21. (本小题 8分 ) 如图是一种儿童的游乐设施—儿童荡板.小明想验证这个荡板上方的四边形是否是平行四边形,现在手头只有一根足够长的绳子,请你帮助他设计一个验证方案,并说明理由.
22. ( 本小题10分 ) 如图,在平行四边形ABCD中,E,F分别是AB,CD的中点,DE,BF与对角线AC分别交于点M,N,连接MF,NE.
(1)求证:DE∥BF
(2)判断四边形MENF是何特殊的四边形?并对结论给予证明;
23. ( 本小题10分 ) 如图,由4个全等的正方形组成L形图案,请按下列要求画图:
(1)在图①中添加1个正方形,使它成轴对称图形(不能是中心对称图形);
(2)在图②中添加1个正方形,使它成中心对称图形(不能是轴对称图形);
(3)在图③中改变1个正方形的位置,从而得到一个新图形,使它既成中心对称图形,又成轴对称图形.
24. ( 本小题12分 ) 如图,平行四边形ABCO位于直角坐标系中,O为坐标原点,点 A(-8,O) ,点 C(3,4)BC 交y轴于点 D. 动点E从点D出发,沿DB方向以每秒1个单位长度的速度终点B运动,同时动点F从点A出发,沿射线OA的方向以每秒2个单位长度的速度运动,当点E运动到点B时,点F随之停止运动,运动时间为 f( 秒 ) .
(1)用t的代数式表示: BE= ________, OF= ________
(2)若以A,B,E,F为顶点的四边形是平行四边形时,求t的值.
(3)当 △BEF 恰好是等腰三角形时,求t的值.
答案解析部分
一、单选题
1. D
考点:轴对称图形,中心对称及中心对称图形
解:A、既不是轴对称图形,也不是中心对称图形,不符合题意,所以本选项错误;
B、既不是轴对称图形,也不是中心对称图形,不符合题意,所以本选项错误;
C、是轴对称图形,不是中心对称图形,不符合题意,所以本选项错误;
D、既是轴对称图形,也是中心对称图形,符合题意,所以本选项正确.
故答案为:D.
分析:在平面内,把一个图形绕着某个点旋转180°,如果旋转后的图形能与原来的图形重合,那么这个图形叫做中心对称图形。
在平面内,如果一个图形沿一条直线折叠,直线两旁的部分能够完全重合,那么这个图形叫做轴对称图形;根据定义并结合图形即可判断求解.
2. B
考点:多边形的对角线
解:∵多边形的边数为8,
∴可分成8-2=6个三角形.
故答案为:B.
分析:n边形从一个顶点引对角线,把n边形分成(n-2)个三角形,据此即可得出答案.
3. C
考点:多边形的对角线,多边形内角与外角
解:多边形的边数 n=720°÷180°+2=6 ;
对角线的条数:6×(6-3)÷2=9.
故答案为:C.
分析:根据n变形内角和公式(n-2)·180°=720,可求出多边形边数,利用n边形对角线为n(n-3)2即可求出结论.
4. C
考点:垂线段最短,平行线的性质,平行线之间的距离
解: ① 两直线平行同旁内角互补,不符合题意;
②直线外一点与直线上各点连接的所有线段中,垂线段最短;符合题意;
③从直线外一点到这条直线的垂线段的长度,叫做点到直线的距离;符合题意;
④平行线间的距离处处相等;符合题意;
故答案为:C.
分析:分别利用同旁内角互补的条件;垂线段的性质;点到直线的距离定义;以及平行间距离的特点进行判断。
5. B
考点:平行四边形的性质
解:∵四边形ABCD是平行四边形,
∴∠A=∠C,∠B=∠D,∠A+∠B=180°,
又∵∠A=2∠B,
∴2∠B+∠B=180°,
解得:∠B=60°,
∴∠D=60°;
故答案为:B.
分析:根据平行四边形的邻边互补,结合已知进行求解.
6. C
考点:勾股定理,平行四边形的性质
解:∵在平行四边形ABCD中,AC、BD相交于点O,AB⊥AC,若AB=4,AC=6,
∴AO=OC= 12 AC=3,CD=AB=4,
∴BO= AB2+AO2=42+32=5 ,
∴OD=BO=5,
∴△COD的周长=OD+OC+CD=5+3+4=12,
故答案为:C.
分析:利用平行四边形的性质和勾股定理易求BO的长,进而可求出OD的长,进而解答即可.
7. A
考点:平行四边形的判定
解:A.∵AB//CD,AB=CD,
∴四边形是平行四边形(一组对边平行且相等的四边形是平行四边形),故A能判定四边形ABCD是平行四边形;
B.如图1,筝形ABCD中,满足AB=BC,AD=CD,但四边形ABCD不是平行四边形;
C.如图2,等腰梯形ABCD中,满足AC=BD,AB=CD,但四边形ABCD不是平行四边形;
D.如图3,等腰梯形ABCD中,满足AB∥CD,AD=CB,但四边形ABCD不是平行四边形;
故答案为:A.
分析:根据平行四边形的判定方法,结合举反例即可判断.
8. C
考点:平行四边形的性质,三角形的中位线定理
解:∵四边形ABCD是平行四边形,
∴O是AC的中点,
∵E是BC的中点,
∴OE是△ABC的中位线,
∴AB=2OE=4,
∴平行四边形ABCD的周长=2(AB+AD)=2×(4+5)=18.
故答案为:C.
分析:根据平行四边形的性质可得O是AC的中点,结合E是BC的中点,可得OE是△ABC的中位线,利用三角形中位线定理可得AB的长,则平行四边形的周长可求.
9. B
考点:反证法
解:用反证法证明“中至少有一个内角不大于 90° ”时,等于应先假设:每一个内角都大于90°.
故答案为:B.
分析:至少有一个内角不大于90°的反面是每一个内角都大于90°,据此即可假设.
10. C
考点:多边形内角与外角
解:根据题意,五边形的内角和为: (5-2)×180°=540° ,
∵ ∠1+∠2+∠3=(180°-∠BCD)+(180°-∠CDE)+(180°-∠AED)
=540°-(∠BCD+∠CDE+∠AED) ,
∵ ∠BCD+∠CDE+∠AED=540°-(∠A+∠B) ,
∴ ∠1+∠2+∠3=540°-(540°-230°)=230° ;
故答案为:C.
分析:先求出五边形的内角和,结合 ∠A+∠B=230° ,即可求出答案.
二、填空题
11. 十
考点:多边形内角与外角
解:设所求n边形边数为n,先根据多边形的外角和为360度得到多边形的内角和,再根据多边形的内角和公式,即可得到结果.
由题意得多边形的内角和为1800°-360°=1440°,
设所求n边形边数为n,则180°(n-2)=1440°,解得n=10,
则此多边形是十边形.
分析:利用多边形的内角和和外角和列式求解即可。
12. 8
考点:平行线之间的距离,三角形的面积
解:在△ABD中,当BD为底时,设高为h,在△AEC中,当AE为底时,设高为h′,因为AE∥BD,所以h=h′,因为△ABD的面积为16,BD=8,所以h=4.则△ACB的面积= 12×4×4 =8.
故答案为:8.
分析:利用平行线间的距离处处相等,根据△ABD的面积及BD的长,可求出BD边上的高,再利用三角形的面积公式可求出△ACE的面积。
13. ②③④
考点:轴对称图形,中心对称及中心对称图形
解:①不是轴对称图形,因为找不到任何这样的一条直线,沿这条直线对折后它的两部分能够重合;即不满足轴对称图形的定义.是中心对称图形,故不符合题意;
②③④都是轴对称图形,也是中心对称图形,故符合题意;
⑤是轴对称图形.不是中心对称图形,因为找不到任何这样的一点,旋转180度后它的两部分能够重合;即不满足中心对称图形的定义.故不符合题意;
故本题答案为:②③④.
分析:根据轴对称图形以及中心对称图形的含义,判断得到答案即可。
14. AE=CF(答案不唯一)
考点:平行四边形的判定与性质
解:如图,连接BD交AC于点O,
∵四边形ABCD为平行四边形,
∴OB=OD,OA=OC,
若AE=CF,则有AO-AE=CO-CF,即OE=OF,
∴四边形BEDF为平行四边形,
故答案为:AE=CF.答案不唯一.
分析:连接BD交AC于点O,由平行四边形的性质可得到OB=OD,要证明四边形BEDF为平行四边形,只需要OE=OF即可,故添加的条件只要能证明OE=OF即可.
15. 4
考点:三角形的面积,三角形的中位线定理
解:∵AD、BE是△ABC的两条中线,
∴DE为△ABC的中位线,
∴DE∥AB , DE= 12 AB ,
∴△ECD∽△ACB ,
∴S△EDC:S△ABC=DE2:AB2=1:4.
S△ABD= 12 S△ABC ,
∴S△EDC:S△ABD=1:2,
∵S△EDC=2
∴S△ABD=4
分析:根据三角形中位线的性质可得DE//AB,DE=12AB,即可得到△ECD∽△ACB , 根据相似三角形的面积比等于相似比的平方即可得到S△EDC:S△ABC的比值,再结合S△ABD= 12 S△ABC进行求解.
16. 6
考点:代数式求值
解:由图可知:五边形内部格点有4个,故 a=4
五边形边上格点有6个,故 b=6
∴ S=a+12b-1 = 4+12×6-1=6
故答案为:6.
分析:根据题目要求,数出五边形内部格点的数量,五边形边上格点的数量,代入 S=a+12b-1 计算即可.
三、解答题
17. 解:∵一个多边形的内角和一定是 180° 的倍数,
∴ a+2680° 是 180° 的倍数,且 0180°×15=2700° ,则 a=20° ,
根据多边形内角和公式 180°(n-2) ,这个多边形的边数是17,这个内角a是 20° .
考点:多边形内角与外角
分析:根据多边形内角和公式可知多边形的内角和度数一定是 180° 的倍数,找到合适的度数,看它是 180° 的几倍,就可以算出边数和内角a的度数.
18. 解: ∵ 四边形ABCD是平行四边形
∴AD//BC,∠D=∠ABC
∴∠CBE=∠AEB
∵∠AEB=27°
∴∠CBE=27°
又 ∵BE 是 ∠ABC 的平分线
∴∠ABC=2∠CBE=54°
∴∠D=54°
故 ∠D 的度数为 54°
考点:平行四边形的性质
分析:先根据平行四边形的性质可得 AD//BC,∠D=∠ABC ,再根据平行线的性质可得 ∠CBE=27° ,然后根据角平分线的定义可得 ∠ABC=54° ,由此即可得出答案.
19. 证明:连接DE,FG,
∵BD ,CE是 △ABC 的中位线,
∴D ,E是AB,AC的中点,
∴DE//BC , DE=12BC ,
同理: FG//BC , FG=12BC ,
∴DE//FG , DE=FG ,
∴ 四边形DEFG是平行四边形,
∴EF//DG , EF=DG .
考点:平行四边形的判定与性质,三角形的中位线定理
分析:连接DE,FG,利用三角形的中位线的性质得到DE//FG,DE=FG,证出四边形DEFG是平行四边形,再利用平行四边形的性质得到EF//DG? , 且?EF=DG? .
20. 证明:假设A≥60°,∵A是不等边三角形ABC的最小角(不妨设C为最大角),∴B≥A≥60°,C>A≥60°,∴A+B+C>180°,与三角形内角和等于180°矛盾,∴假设错误,原结论成立,即A<60°.
考点:反证法
分析:用反证法证明。首先否定结论即假设A≥60°,根据已知条件A是不等边三角形ABC的最小角(不妨设C为最大角),由三角形内角和定理可得B≥A≥60°,C>A≥60°,所以A+B+C>180°,与三角形内角和等于180°矛盾,所以原命题成立,即A<60°.
21. 解:方案:先用绳子测量出四边形ABCD的边AB的长,并在绳子上做上标记,然后再用这根绳子测量出CD的长度做上标记,比较AB与CD的长短,用同样的方法比较BC、AD的长短,如果AB=CD,BC=AD,则四边形ABCD是平行四边形.
理由:两组对边对应相等的四边形是平行四边形
考点:平行四边形的判定
分析:本题是应用题,主要考查的是平行四边形的判定,掌握平行四边形的判定定理是解题的关键,根据两组对边相等的四边形是平行四边形进行判定即可.
22. (1)证明:在平行四边形ABCD中,AB∥CD,AB=CD,
∵E,F分别是AB,CD的中点,
∴DF=BE,DF∥BE,
∴四边形DEBF为平行四边形,
∴DE∥BF
(2)解:MENF为平行四边形,理由是:
如图,∵DE∥BF,
∴∠FNC=∠DMC=∠AME,
又∵DC∥AB,
∴∠ACD=∠CAB,又CF=AE= 12 AB= 12 CD,
∴△FNC≌EMA(AAS),
∴FN=EM,又FN∥EM,
∴MENF为平行四边形.
考点:平行四边形的判定与性质
分析:(1)根据已知条件证明四边形DEBF为平行四边形,即可得到;(2)证明△FNC≌EMA,得到FN=EM,又FN∥EM,可得结果.
23. (1)解:答案不唯一.如图a,图b,图c所示.
(2)解:如图d所示.
(3)解:答案不唯一.如图e.图f所示.
考点:轴对称图形,中心对称及中心对称图形
分析:(1)根据轴对称图形的性质,先找出对称轴,再思考如何画图;(2)如(1),也是先找一个中心,再根据中心对称的性质,思考如何画图;(3)根据中心对称和轴对称的性质画一个图形.
注意此题有多种画法,答案不唯一.
24. (1)5-t;OF=2t
(2)解: ① 当F在A点右侧,四边形ABEF为平行四边形, BE=AF ,
即 8-2t=5-t ,解得 t=3 ,
② 当P在A点左侧,四边形BEAF为平行四边形, BE=AF ,即 5-t=2t-8 ,
解得 t=133 ;
(3)解:当 △BEF 恰好是等腰三角形时,有以下三种情况:
① 当 BF=EF 时, 5-2t=t ,解得 t=53 ;
② 当 EB=FB 时, (5-t)2=16+(5-2t)2 ,方程无解;
③ 当 BE=FE 时, (5-t)2=16+t2 ,解得 t=910 ;
所以,当 t=53 或 t=910 时,当 △BEF 恰好是等腰三角形.
考点:坐标与图形性质,等腰三角形的判定,平行四边形的性质
分析:(1根据题意,可得点B的坐标为 (-5,4) ,即可求得 BE=5-t , OF=2f ;(2分两种情况讨论: ① 当F在A点右侧,四边形ABEF为平行四边形, BE=AF ; ② 当P在A点左侧,四边形BEAF为平行四边形, BE=AF ,列方程求解即可;(3分三种情况讨论: ① 当 BF=EF 时; ② 当 EB=FB 时; ③ 当 BE=FE 时,分别列方程求解即可.
一、单选题(本大题共10小题,每小题3分,共30分。)
1. 下面列图案中既是轴对称图形又是中心对称图形的是(?? )
A.????????????????B.????????????????C.????????????????D.?
2. 从八边形的一个顶点引对角线,最多把它分割成三角形的个数为(?? )
A.?5???????????????????????????????????????????B.?6???????????????????????????????????????????C.?7???????????????????????????????????????????D.?8
3. 一个多边形内角和是720?,则这个多边形的对角线条数为(??? )
A.?3???????????????????????????????????????????B.?6???????????????????????????????????????????C.?9???????????????????????????????????????????D.?12
4. 下列说法中,正确的个数有:( ??)
①同旁内角互补;②直线外一点与直线上各点连接的所有线段中,垂线段最短;③从直线外一点到这条直线的垂线段的长度,叫做点到直线的距离;④平行线间的距离处处相等.
A.?1个???????????????????????????????????????B.?2个???????????????????????????????????????C.?3个???????????????????????????????????????D.?4个
5. 在平行四边形 ABCD 中,若 ∠A=2∠B ,则 ∠D 的度数是(? )
A.?50°???????????????????????????????????????B.?60°???????????????????????????????????????C.?70°???????????????????????????????????????D.?80°
6. 如图,在 ?ABCD 中, AC 、 BD 相交于点O, AB⊥AC ,若 AB=4 , AC=6 ,则 ΔCOD 的周长是(?? )
A.?8?????????????????????????????????????????B.?10?????????????????????????????????????????C.?12?????????????????????????????????????????D.?16
7. 能判定四边形ABCD是平行四边形的是(??? )
A.?AB∥CD,AB=CD???????????B.?AB=BC,AD=CD???????????C.?AC=BD,AB=CD???????????D.?AB∥CD,AD=CB
8. 如图,在平行四边形ABCD中,对角线AC,BD交于点O,E是BC边上的中点,若 OE=2,AD=5 ,则平行四边形ABCD的周长为(? )?
?
A.?9?????????????????????????????????????????B.?16?????????????????????????????????????????C.?18?????????????????????????????????????????D.?20
9. 用反证法证明命题“在四边形中至少有一个内角不大于90°”时,首先应假设(?? )
A.?每个内角都小于90°
B.?每个内角都大于90°
C.?没有一个内角大于90°
D.?每个内角都等于90°
10. 如图 ∠1,∠2,∠3 是正五边形 ABCDE 的三个外角,若 ∠A+∠B=230°, 则 ∠1+∠2+∠3 =(??? )
A.?140°?????????????????????????????????B.?180°?????????????????????????????????C.?230°?????????????????????????????????D.?320°
二、填空题(本大题共6小题,每小题4分,共24分。)
11. 若一个多边形的内角和与外角和之和是1800°,则此多边形是________边形.
12. 如图,直线AE∥BD,点C在BD上,若AE=4,BD=8,△ABD的面积为16,则 △ACE 的面积为________.
13. 在①平行四边形;②矩形;③菱形;④正方形;⑤等腰梯形这五种图形中,既是轴对称图形又是中心对称图形的是________(只填序号).
14. 如图,在平行四边形 ABCD 中, E,F 两点均在对角线 AC 上.要使四边形 BEDF 为平行四边形,在不添加辅助线的情况下,需要增加的一个条件是________(写出一个即可).
?
15. 如图,AD、BE是△ABC的两条中线,△EDC的面积是2,则△ABD的面积是________.
16. 各顶点都在方格纸的格点(横竖格子线的交错点)上的多边形称为格点多边形,它的面积S可用公式 S=a+12b-1 (a是多边形内的格点数,b是多边形边界上的格点数)计算,这个公式称为“皮克(Pick)定理”.如图给出了一个格点五边形,则该五边形的面积 S= ________.
三、解答题(本大题共8小题,共66分。)
17. (本小题 6分 ) 一个多边形除了一个内角a外,其余内角的和为2680°,求这个多边形的边数和这个内角a的度数.
18. (本小题 6分 ) 如图,在 ?ABCD 中,∠ABC的平分线BE交AD于点E,测得∠AEB=27°,求∠D的度数.
19. ( 本小题6分 )△ABC 的中线BD,CE相交于O,F,G分别是BO,CO的中点,求证: EF//DG ,且 EF=DG .
20. ( 本小题8分 ) 在不等边△ABC中,A是最小角,求证:A<60°.
21. (本小题 8分 ) 如图是一种儿童的游乐设施—儿童荡板.小明想验证这个荡板上方的四边形是否是平行四边形,现在手头只有一根足够长的绳子,请你帮助他设计一个验证方案,并说明理由.
22. ( 本小题10分 ) 如图,在平行四边形ABCD中,E,F分别是AB,CD的中点,DE,BF与对角线AC分别交于点M,N,连接MF,NE.
(1)求证:DE∥BF
(2)判断四边形MENF是何特殊的四边形?并对结论给予证明;
23. ( 本小题10分 ) 如图,由4个全等的正方形组成L形图案,请按下列要求画图:
(1)在图①中添加1个正方形,使它成轴对称图形(不能是中心对称图形);
(2)在图②中添加1个正方形,使它成中心对称图形(不能是轴对称图形);
(3)在图③中改变1个正方形的位置,从而得到一个新图形,使它既成中心对称图形,又成轴对称图形.
24. ( 本小题12分 ) 如图,平行四边形ABCO位于直角坐标系中,O为坐标原点,点 A(-8,O) ,点 C(3,4)BC 交y轴于点 D. 动点E从点D出发,沿DB方向以每秒1个单位长度的速度终点B运动,同时动点F从点A出发,沿射线OA的方向以每秒2个单位长度的速度运动,当点E运动到点B时,点F随之停止运动,运动时间为 f( 秒 ) .
(1)用t的代数式表示: BE= ________, OF= ________
(2)若以A,B,E,F为顶点的四边形是平行四边形时,求t的值.
(3)当 △BEF 恰好是等腰三角形时,求t的值.
答案解析部分
一、单选题
1. D
考点:轴对称图形,中心对称及中心对称图形
解:A、既不是轴对称图形,也不是中心对称图形,不符合题意,所以本选项错误;
B、既不是轴对称图形,也不是中心对称图形,不符合题意,所以本选项错误;
C、是轴对称图形,不是中心对称图形,不符合题意,所以本选项错误;
D、既是轴对称图形,也是中心对称图形,符合题意,所以本选项正确.
故答案为:D.
分析:在平面内,把一个图形绕着某个点旋转180°,如果旋转后的图形能与原来的图形重合,那么这个图形叫做中心对称图形。
在平面内,如果一个图形沿一条直线折叠,直线两旁的部分能够完全重合,那么这个图形叫做轴对称图形;根据定义并结合图形即可判断求解.
2. B
考点:多边形的对角线
解:∵多边形的边数为8,
∴可分成8-2=6个三角形.
故答案为:B.
分析:n边形从一个顶点引对角线,把n边形分成(n-2)个三角形,据此即可得出答案.
3. C
考点:多边形的对角线,多边形内角与外角
解:多边形的边数 n=720°÷180°+2=6 ;
对角线的条数:6×(6-3)÷2=9.
故答案为:C.
分析:根据n变形内角和公式(n-2)·180°=720,可求出多边形边数,利用n边形对角线为n(n-3)2即可求出结论.
4. C
考点:垂线段最短,平行线的性质,平行线之间的距离
解: ① 两直线平行同旁内角互补,不符合题意;
②直线外一点与直线上各点连接的所有线段中,垂线段最短;符合题意;
③从直线外一点到这条直线的垂线段的长度,叫做点到直线的距离;符合题意;
④平行线间的距离处处相等;符合题意;
故答案为:C.
分析:分别利用同旁内角互补的条件;垂线段的性质;点到直线的距离定义;以及平行间距离的特点进行判断。
5. B
考点:平行四边形的性质
解:∵四边形ABCD是平行四边形,
∴∠A=∠C,∠B=∠D,∠A+∠B=180°,
又∵∠A=2∠B,
∴2∠B+∠B=180°,
解得:∠B=60°,
∴∠D=60°;
故答案为:B.
分析:根据平行四边形的邻边互补,结合已知进行求解.
6. C
考点:勾股定理,平行四边形的性质
解:∵在平行四边形ABCD中,AC、BD相交于点O,AB⊥AC,若AB=4,AC=6,
∴AO=OC= 12 AC=3,CD=AB=4,
∴BO= AB2+AO2=42+32=5 ,
∴OD=BO=5,
∴△COD的周长=OD+OC+CD=5+3+4=12,
故答案为:C.
分析:利用平行四边形的性质和勾股定理易求BO的长,进而可求出OD的长,进而解答即可.
7. A
考点:平行四边形的判定
解:A.∵AB//CD,AB=CD,
∴四边形是平行四边形(一组对边平行且相等的四边形是平行四边形),故A能判定四边形ABCD是平行四边形;
B.如图1,筝形ABCD中,满足AB=BC,AD=CD,但四边形ABCD不是平行四边形;
C.如图2,等腰梯形ABCD中,满足AC=BD,AB=CD,但四边形ABCD不是平行四边形;
D.如图3,等腰梯形ABCD中,满足AB∥CD,AD=CB,但四边形ABCD不是平行四边形;
故答案为:A.
分析:根据平行四边形的判定方法,结合举反例即可判断.
8. C
考点:平行四边形的性质,三角形的中位线定理
解:∵四边形ABCD是平行四边形,
∴O是AC的中点,
∵E是BC的中点,
∴OE是△ABC的中位线,
∴AB=2OE=4,
∴平行四边形ABCD的周长=2(AB+AD)=2×(4+5)=18.
故答案为:C.
分析:根据平行四边形的性质可得O是AC的中点,结合E是BC的中点,可得OE是△ABC的中位线,利用三角形中位线定理可得AB的长,则平行四边形的周长可求.
9. B
考点:反证法
解:用反证法证明“中至少有一个内角不大于 90° ”时,等于应先假设:每一个内角都大于90°.
故答案为:B.
分析:至少有一个内角不大于90°的反面是每一个内角都大于90°,据此即可假设.
10. C
考点:多边形内角与外角
解:根据题意,五边形的内角和为: (5-2)×180°=540° ,
∵ ∠1+∠2+∠3=(180°-∠BCD)+(180°-∠CDE)+(180°-∠AED)
=540°-(∠BCD+∠CDE+∠AED) ,
∵ ∠BCD+∠CDE+∠AED=540°-(∠A+∠B) ,
∴ ∠1+∠2+∠3=540°-(540°-230°)=230° ;
故答案为:C.
分析:先求出五边形的内角和,结合 ∠A+∠B=230° ,即可求出答案.
二、填空题
11. 十
考点:多边形内角与外角
解:设所求n边形边数为n,先根据多边形的外角和为360度得到多边形的内角和,再根据多边形的内角和公式,即可得到结果.
由题意得多边形的内角和为1800°-360°=1440°,
设所求n边形边数为n,则180°(n-2)=1440°,解得n=10,
则此多边形是十边形.
分析:利用多边形的内角和和外角和列式求解即可。
12. 8
考点:平行线之间的距离,三角形的面积
解:在△ABD中,当BD为底时,设高为h,在△AEC中,当AE为底时,设高为h′,因为AE∥BD,所以h=h′,因为△ABD的面积为16,BD=8,所以h=4.则△ACB的面积= 12×4×4 =8.
故答案为:8.
分析:利用平行线间的距离处处相等,根据△ABD的面积及BD的长,可求出BD边上的高,再利用三角形的面积公式可求出△ACE的面积。
13. ②③④
考点:轴对称图形,中心对称及中心对称图形
解:①不是轴对称图形,因为找不到任何这样的一条直线,沿这条直线对折后它的两部分能够重合;即不满足轴对称图形的定义.是中心对称图形,故不符合题意;
②③④都是轴对称图形,也是中心对称图形,故符合题意;
⑤是轴对称图形.不是中心对称图形,因为找不到任何这样的一点,旋转180度后它的两部分能够重合;即不满足中心对称图形的定义.故不符合题意;
故本题答案为:②③④.
分析:根据轴对称图形以及中心对称图形的含义,判断得到答案即可。
14. AE=CF(答案不唯一)
考点:平行四边形的判定与性质
解:如图,连接BD交AC于点O,
∵四边形ABCD为平行四边形,
∴OB=OD,OA=OC,
若AE=CF,则有AO-AE=CO-CF,即OE=OF,
∴四边形BEDF为平行四边形,
故答案为:AE=CF.答案不唯一.
分析:连接BD交AC于点O,由平行四边形的性质可得到OB=OD,要证明四边形BEDF为平行四边形,只需要OE=OF即可,故添加的条件只要能证明OE=OF即可.
15. 4
考点:三角形的面积,三角形的中位线定理
解:∵AD、BE是△ABC的两条中线,
∴DE为△ABC的中位线,
∴DE∥AB , DE= 12 AB ,
∴△ECD∽△ACB ,
∴S△EDC:S△ABC=DE2:AB2=1:4.
S△ABD= 12 S△ABC ,
∴S△EDC:S△ABD=1:2,
∵S△EDC=2
∴S△ABD=4
分析:根据三角形中位线的性质可得DE//AB,DE=12AB,即可得到△ECD∽△ACB , 根据相似三角形的面积比等于相似比的平方即可得到S△EDC:S△ABC的比值,再结合S△ABD= 12 S△ABC进行求解.
16. 6
考点:代数式求值
解:由图可知:五边形内部格点有4个,故 a=4
五边形边上格点有6个,故 b=6
∴ S=a+12b-1 = 4+12×6-1=6
故答案为:6.
分析:根据题目要求,数出五边形内部格点的数量,五边形边上格点的数量,代入 S=a+12b-1 计算即可.
三、解答题
17. 解:∵一个多边形的内角和一定是 180° 的倍数,
∴ a+2680° 是 180° 的倍数,且 0
根据多边形内角和公式 180°(n-2) ,这个多边形的边数是17,这个内角a是 20° .
考点:多边形内角与外角
分析:根据多边形内角和公式可知多边形的内角和度数一定是 180° 的倍数,找到合适的度数,看它是 180° 的几倍,就可以算出边数和内角a的度数.
18. 解: ∵ 四边形ABCD是平行四边形
∴AD//BC,∠D=∠ABC
∴∠CBE=∠AEB
∵∠AEB=27°
∴∠CBE=27°
又 ∵BE 是 ∠ABC 的平分线
∴∠ABC=2∠CBE=54°
∴∠D=54°
故 ∠D 的度数为 54°
考点:平行四边形的性质
分析:先根据平行四边形的性质可得 AD//BC,∠D=∠ABC ,再根据平行线的性质可得 ∠CBE=27° ,然后根据角平分线的定义可得 ∠ABC=54° ,由此即可得出答案.
19. 证明:连接DE,FG,
∵BD ,CE是 △ABC 的中位线,
∴D ,E是AB,AC的中点,
∴DE//BC , DE=12BC ,
同理: FG//BC , FG=12BC ,
∴DE//FG , DE=FG ,
∴ 四边形DEFG是平行四边形,
∴EF//DG , EF=DG .
考点:平行四边形的判定与性质,三角形的中位线定理
分析:连接DE,FG,利用三角形的中位线的性质得到DE//FG,DE=FG,证出四边形DEFG是平行四边形,再利用平行四边形的性质得到EF//DG? , 且?EF=DG? .
20. 证明:假设A≥60°,∵A是不等边三角形ABC的最小角(不妨设C为最大角),∴B≥A≥60°,C>A≥60°,∴A+B+C>180°,与三角形内角和等于180°矛盾,∴假设错误,原结论成立,即A<60°.
考点:反证法
分析:用反证法证明。首先否定结论即假设A≥60°,根据已知条件A是不等边三角形ABC的最小角(不妨设C为最大角),由三角形内角和定理可得B≥A≥60°,C>A≥60°,所以A+B+C>180°,与三角形内角和等于180°矛盾,所以原命题成立,即A<60°.
21. 解:方案:先用绳子测量出四边形ABCD的边AB的长,并在绳子上做上标记,然后再用这根绳子测量出CD的长度做上标记,比较AB与CD的长短,用同样的方法比较BC、AD的长短,如果AB=CD,BC=AD,则四边形ABCD是平行四边形.
理由:两组对边对应相等的四边形是平行四边形
考点:平行四边形的判定
分析:本题是应用题,主要考查的是平行四边形的判定,掌握平行四边形的判定定理是解题的关键,根据两组对边相等的四边形是平行四边形进行判定即可.
22. (1)证明:在平行四边形ABCD中,AB∥CD,AB=CD,
∵E,F分别是AB,CD的中点,
∴DF=BE,DF∥BE,
∴四边形DEBF为平行四边形,
∴DE∥BF
(2)解:MENF为平行四边形,理由是:
如图,∵DE∥BF,
∴∠FNC=∠DMC=∠AME,
又∵DC∥AB,
∴∠ACD=∠CAB,又CF=AE= 12 AB= 12 CD,
∴△FNC≌EMA(AAS),
∴FN=EM,又FN∥EM,
∴MENF为平行四边形.
考点:平行四边形的判定与性质
分析:(1)根据已知条件证明四边形DEBF为平行四边形,即可得到;(2)证明△FNC≌EMA,得到FN=EM,又FN∥EM,可得结果.
23. (1)解:答案不唯一.如图a,图b,图c所示.
(2)解:如图d所示.
(3)解:答案不唯一.如图e.图f所示.
考点:轴对称图形,中心对称及中心对称图形
分析:(1)根据轴对称图形的性质,先找出对称轴,再思考如何画图;(2)如(1),也是先找一个中心,再根据中心对称的性质,思考如何画图;(3)根据中心对称和轴对称的性质画一个图形.
注意此题有多种画法,答案不唯一.
24. (1)5-t;OF=2t
(2)解: ① 当F在A点右侧,四边形ABEF为平行四边形, BE=AF ,
即 8-2t=5-t ,解得 t=3 ,
② 当P在A点左侧,四边形BEAF为平行四边形, BE=AF ,即 5-t=2t-8 ,
解得 t=133 ;
(3)解:当 △BEF 恰好是等腰三角形时,有以下三种情况:
① 当 BF=EF 时, 5-2t=t ,解得 t=53 ;
② 当 EB=FB 时, (5-t)2=16+(5-2t)2 ,方程无解;
③ 当 BE=FE 时, (5-t)2=16+t2 ,解得 t=910 ;
所以,当 t=53 或 t=910 时,当 △BEF 恰好是等腰三角形.
考点:坐标与图形性质,等腰三角形的判定,平行四边形的性质
分析:(1根据题意,可得点B的坐标为 (-5,4) ,即可求得 BE=5-t , OF=2f ;(2分两种情况讨论: ① 当F在A点右侧,四边形ABEF为平行四边形, BE=AF ; ② 当P在A点左侧,四边形BEAF为平行四边形, BE=AF ,列方程求解即可;(3分三种情况讨论: ① 当 BF=EF 时; ② 当 EB=FB 时; ③ 当 BE=FE 时,分别列方程求解即可.
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
