1.4全等三角形

(共23张PPT)
A
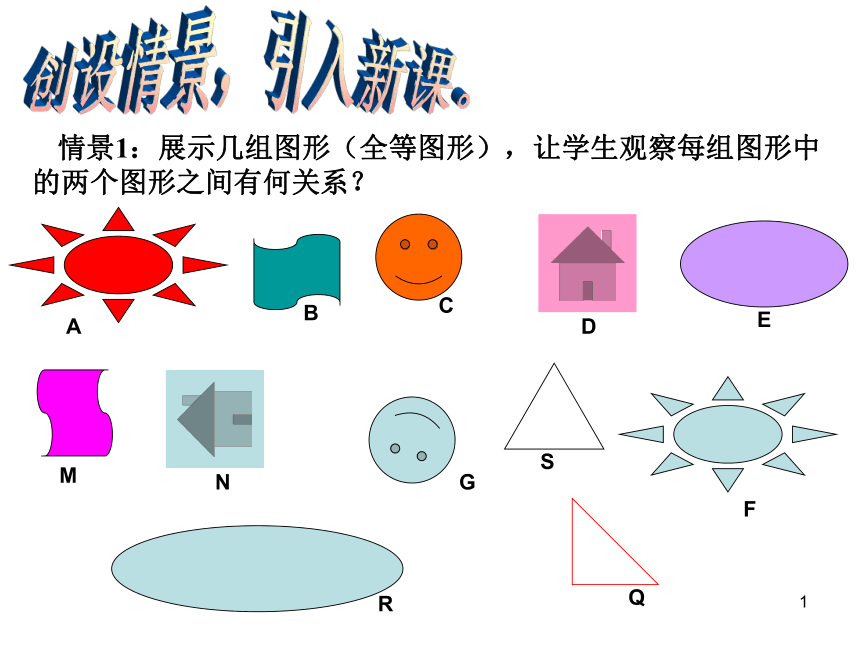
情景1：展示几组图形（全等图形），让学生观察每组图形中的两个图形之间有何关系？
G
F
E
C
D
B
S
R
N
M
Q
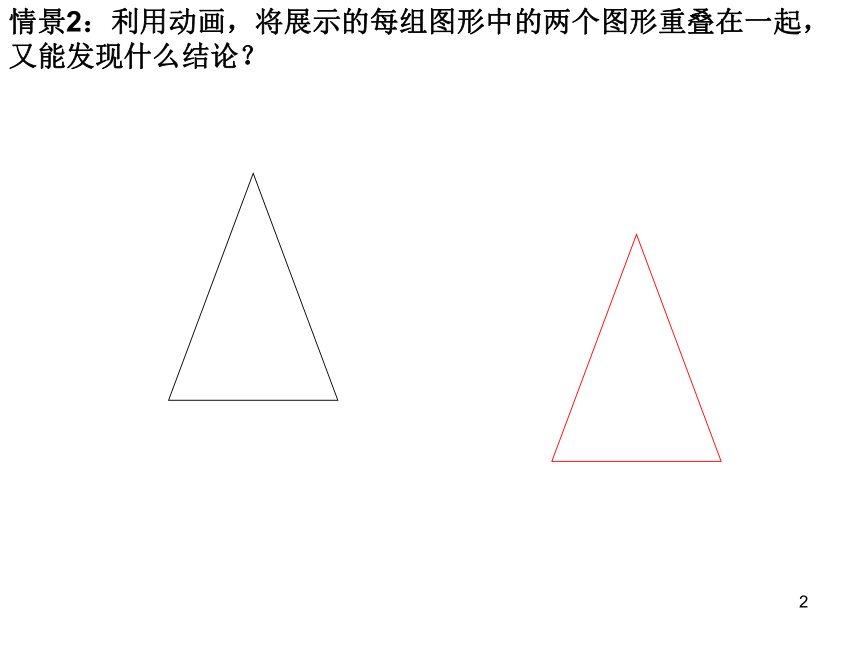
情景2：利用动画，将展示的每组图形中的两个图形重叠在一起， 又能发现什么结论？
2、说一说：你能举出生活中的一些全等图形的例子吗？
3、剪一剪：利用剪刀，你能剪出一些全等的图形吗？
1.全等图形的定义：能够重合的图形称为
全等图形。
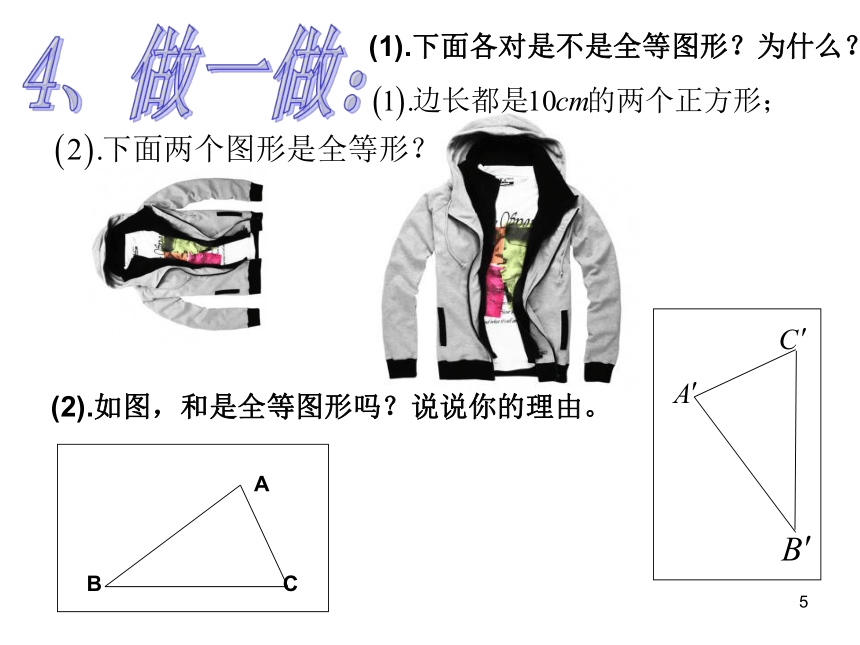
(1).下面各对是不是全等图形？为什么？
(2).如图，和是全等图形吗？说说你的理由。
A
B
C
全等三角形定义：能够重合的两个三角形叫做
全等三角形。
相关的概念：两个全等三角形重合时，互相重合的顶点叫做全等三角形的对应顶点；互相重合的边叫做全等三角形的对应边；互相重合的角叫做全等三角形的对应角。
记作：全等的符号为“≌”。
例如：如图，△ABC与△A′B′C′全等，记作△ABC≌△A′B′C′，
对应顶点为：点A与点A′，点B与点B′，点C与点C′；
对应边为：AB与A′B′，AC与A′C′，BC与B′C′；
对应角为：∠A与∠A′，∠B与∠B′，∠C与∠C′。
注意：记全等三角形时，应将对应顶点的字母写在对应的位置上。
C
B
A
B′
C′
A′
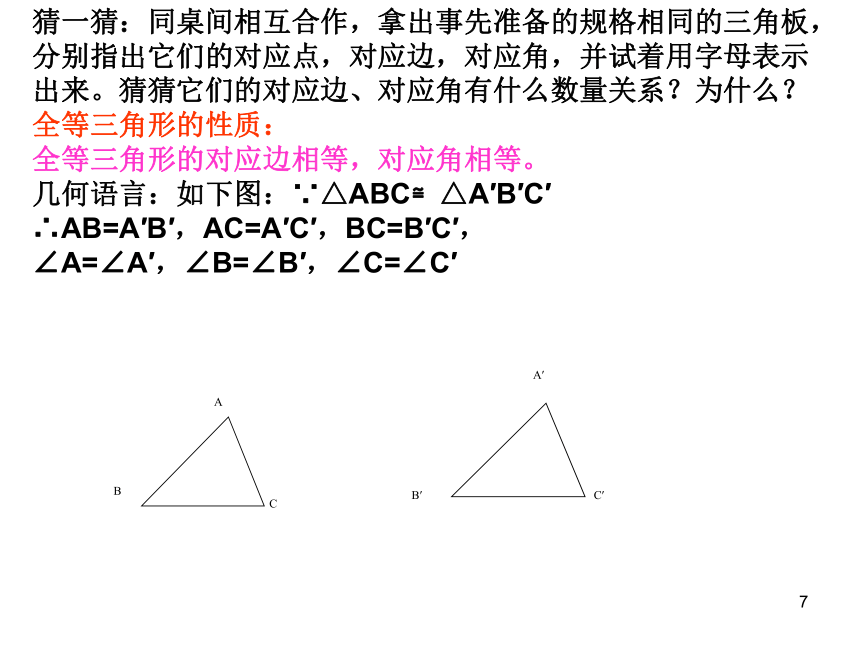
猜一猜：同桌间相互合作，拿出事先准备的规格相同的三角板，分别指出它们的对应点，对应边，对应角，并试着用字母表示出来。猜猜它们的对应边、对应角有什么数量关系？为什么？
全等三角形的性质：
全等三角形的对应边相等，对应角相等。
几何语言：如下图：∵△ABC≌△A′B′C′
∴AB=A′B′，AC=A′C′，BC=B′C′，
∠A=∠A′，∠B=∠B′，∠C=∠C′
C
B
A
B′
C′
A′
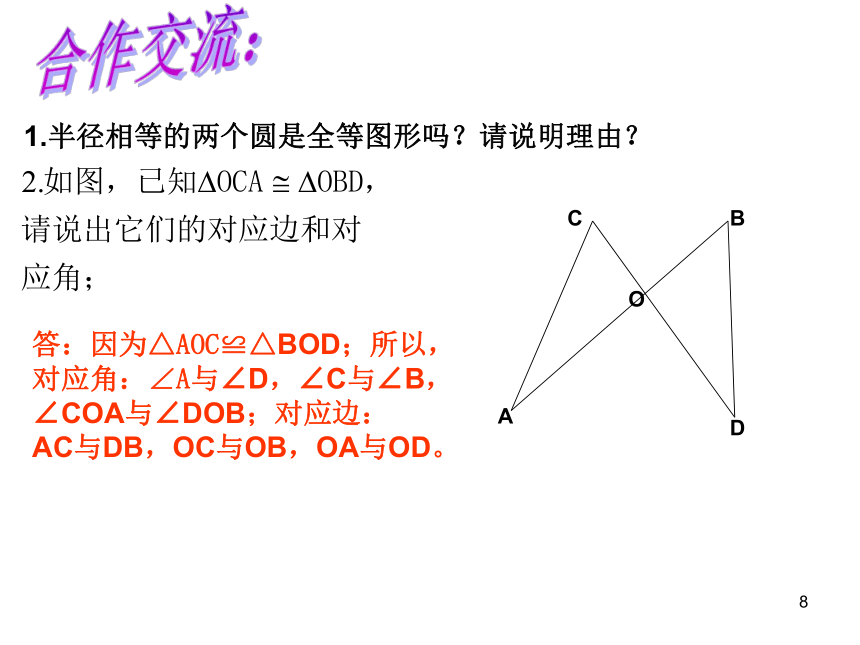
1.半径相等的两个圆是全等图形吗？请说明理由？
A
O
D
C
B
答：因为△AOC≌△BOD；所以，
对应角：∠A与∠D，∠C与∠B，
∠COA与∠DOB；对应边：
AC与DB，OC与OB，OA与OD。
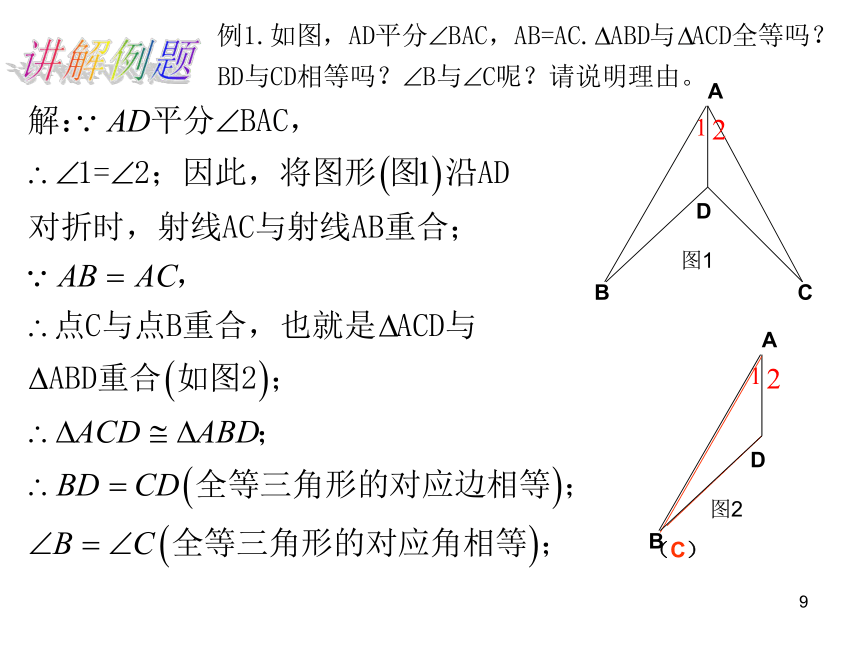
A
D
C
B
A
D
B
（C）
图1
图2
如图所示,已知ΔABC≌ΔADE,则图中与∠BAD相等的角是 .
∠CAE
如图，已知AB＝AC，AE＝AD，∠1＝∠2，你能说明△ABD≌△ACE吗？
如图，PB平分∠ABC,AC和BP垂直,PD⊥BC,PE⊥AB,
D,E分别为垂足.
说明ΔABP≌ΔCBP的理由;
说明AE=CD的理由.
1、如图，△ABC≌△EFD，A和E、B和F是
对应顶点，则它们的对应边是 。
2、如图，将△ABC绕其顶点A顺时针旋转30 度后，得△ADE。
（1）、△ABC与△ADE的关系如何？
（2）、求∠BAD的度数。
A
D
E
C
B
3、已知△ABC≌△DEF，∠A=50 ，∠B=35，ED=8，
则∠F= ，AB= 。
4.如图，已知△ABC≌△EFC，
且CF=5cm，∠EFC=65，
求∠B的度数和BC的长。
0
0
0
我的收获是 … …
我感受到了… …
我的问题存在于… …
§1.4全等三角形
1.全等形的概念 (1)定义：能够重合的两个图形。
(2)说明：全等形关注的是两个图形的形状和大小，而不关心图形的位置。
(3)判断方法：看两个图形是否全等，只要把它们叠合在一起，看是否重合，
重合即为全等形。
2.全等三角形的定义和表示法
(1)定义：能够重合的两个三角形叫做全等三角形。
(2)有关概念：①对应点：两个全等三角形重合时，能互相重合的顶点
叫做全等三角形的对应点。
②对应边：相互重合的边叫做全等三角形对应边。
③对应角：相互重合的角叫做全等三角形对应角。
(3)注意事项：“全等”用“≌”表示，读作“全等于”；记两个三角形全等时，
通常把表示对应点的字母写在对应的位置上。
3.全等三角形的性质
性质：全等三角形的对应边相等；对应角相等。
1.全等形只是位置不同，它们的对应边，
对应角，周长，面积都分别相等；
2.在确定三角形的对应边、对应角时，
可根据“相等的边是对应边，相等的角
是对应角；对应角所对的边是对应边，
对应边所对的角是对应角”来确定。
3.等量代换思想在证明和计算中经常用到。
【1】、复习、整理、巩固今天所学知识。
一、必做题：1、作业本(2)第2—3页T1—T7；
2、参书第16页A组题T1—T3；
二、选做题：1、参书第16页B组题T4；
2.拓展探究题：参看幻灯片第19--21号。
【2】、书面作业
三、抄写幻灯片第17、18张。
1.如图，已知△ABC ≌△CDA，点C与A是对应
点。(1)若在△ACD中，∠1=40度， ∠2=80度，求
∠3的度数； (2)已知△ABC的周长为38,AD+CD
=25，求AC 的长。
A
D
C
B
2.如图所示，若△ABD≌△ACD，∠BAC=52度，
AD是BC边上的高，BC=20厘米，求∠C的度数
和BD的长
A
C
B
D
3.如图所示，将该图形沿OG对折后两侧能够完全重合，若∠A=25°，∠DOC=90°，求∠AED
的度数。
A
B
C
D
E
F
G
O