2.2一元二次方程的解法（1）

(共14张PPT)
2.2 一元二次方程的解法（1）
如图是一块正方形的大理石地砖，已知它的面积为0.81平方米。如果设边长为x米，则可列方程：________.
X2=0.81
（不符）
解：X2 = 0.81,
∴正方形的边长为0.9米
x2=a
a
（a≥0）
一般地,对于形如x2=a 的方程，根据平方根的定义,可解得 ：
这种解一元二次方程的方法叫做开平方法.
(1)解法依据：
(2)有解条件：
平方根的意义。
a≥0
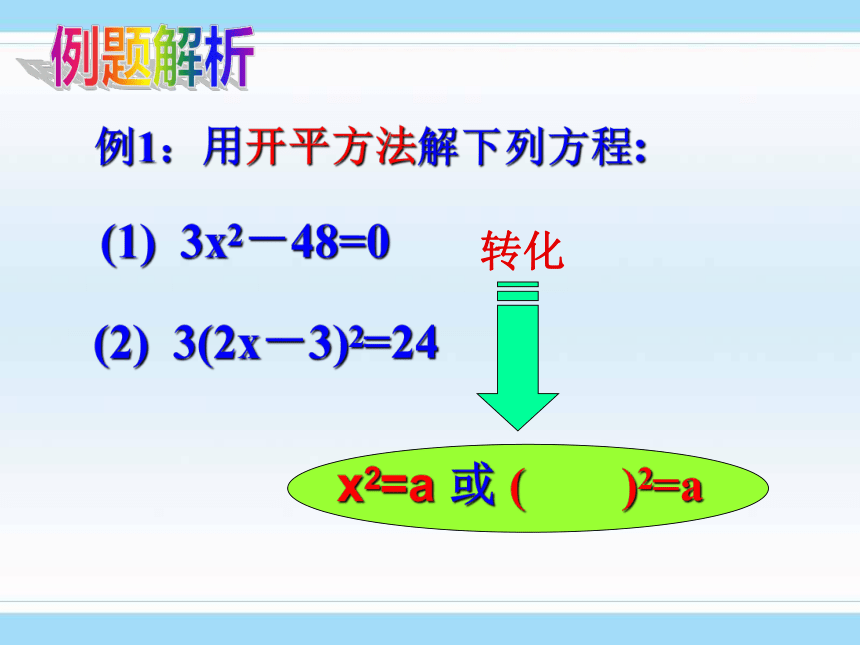
例1：用开平方法解下列方程:
(1) 3x2－48=0
(2) 3(2x－3)2=24
x2=a 或 ( )2=a
转化
练习1：用开平方法解下列方程:
(2) 3(2x－1)2=21
(1) 4x2－3=0
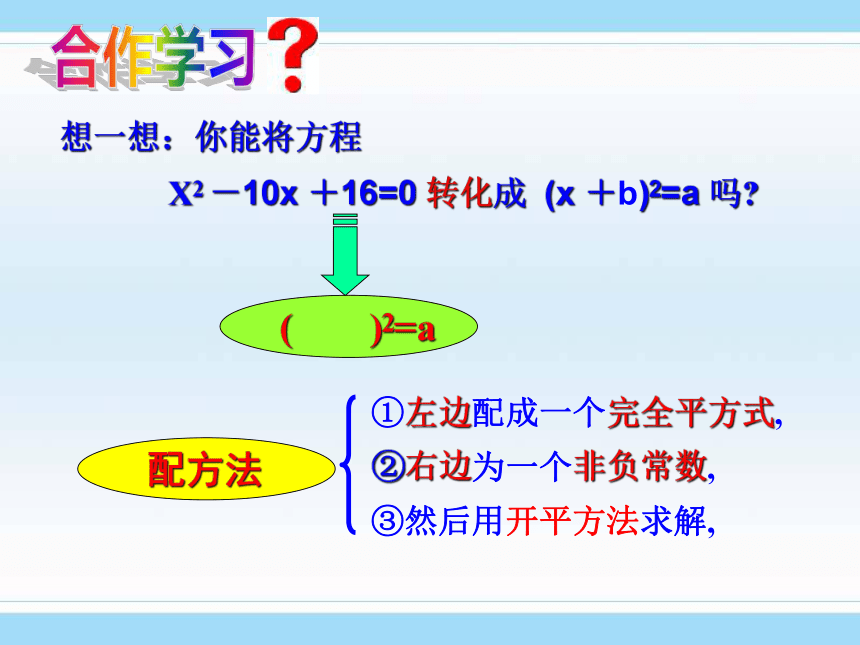
想一想：你能将方程
X2 －10x ＋16=0 转化成 (x ＋b)2=a 吗
( )2=a
①左边配成一个完全平方式,
②右边为一个非负常数,
③然后用开平方法求解,
配方法
(1) x2＋2x＋ =(x＋ )2
二次项系数为1时,配上的是一次项系数一半的平方.
(2) x2－12x＋ =(x－ )2
1
36
6
1
(3) x2－5x＋ =(x － )2
练习2：添上一个恰当的数，使下列多项式
成为一个完全平方式
(4) x2＋2ax＋ =(x+ )2
a2
a
例2：用配方法解下列方程
(1)x2 + 6x=1
(2) 6－x2=5x
①　移项
②　配方
③　开方
④　求解
基本步骤
思考：先用配方法解下列方程：
x2－4x＋7＝0
然后回答下列问题：
（1）你在求解过程中遇到什么问题？
你是怎样处理所遇到的问题的？
（2）对于形如 X2＋px＋q＝0 的方程，
在什么条件下才会有实数根？
1.你掌握了哪些方法？
2.你有什么体验？
直接开方法
配方法
学会转化
( )2=a
练习2：用配方法解下列方程:
(1) x2－2x－4 =0
(2) －x2＋3x＋4 =0
如图,工人师傅
为了修屋顶，把一梯
子搁在墙上,梯子与
屋檐的接触处到底端
的长AB=5米,墙高AC
=4米,问梯子底端点离
墙的距离是多少
A
B
C
布置作业:
1、作业本
2、同步练习