2020-2021学年浙教版八年级数学下册 第5章特殊的平行四边形单元测验试卷(Word版 含答案)
文档属性
| 名称 | 2020-2021学年浙教版八年级数学下册 第5章特殊的平行四边形单元测验试卷(Word版 含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-25 00:00:00 | ||
图片预览



文档简介
浙教版八年级数学下册2020-2021年第5章特殊的平行四边形单元测验试卷
一、单选题
1.下列命题中,假命题是( )
A.对角线互相垂直的四边形是菱形
B.正方形的对角线互相垂直平分
C.矩形的对角线相等
D.对角线互相平分的四边形是平行四边形
2.如图,在平面直角坐标系xOy中,正方形ABCD的顶点D在y轴上,且A(﹣3,0),B(2,b),则b的值为( )
A.3 B.2 C.﹣3 D.﹣2
3.矩形中,点M在对角线上,过M作的平行线交于E,交于F,连接和,已知,,则图中阴影部分的面积是( )
A.12 B.10 C.8 D.6
4.如图,在矩形中,点,分别在边和上,把该矩形沿折叠,使点恰好落在边的点处,已知矩形的面积为,,则折痕的长为( )
A. B.2 C. D.4
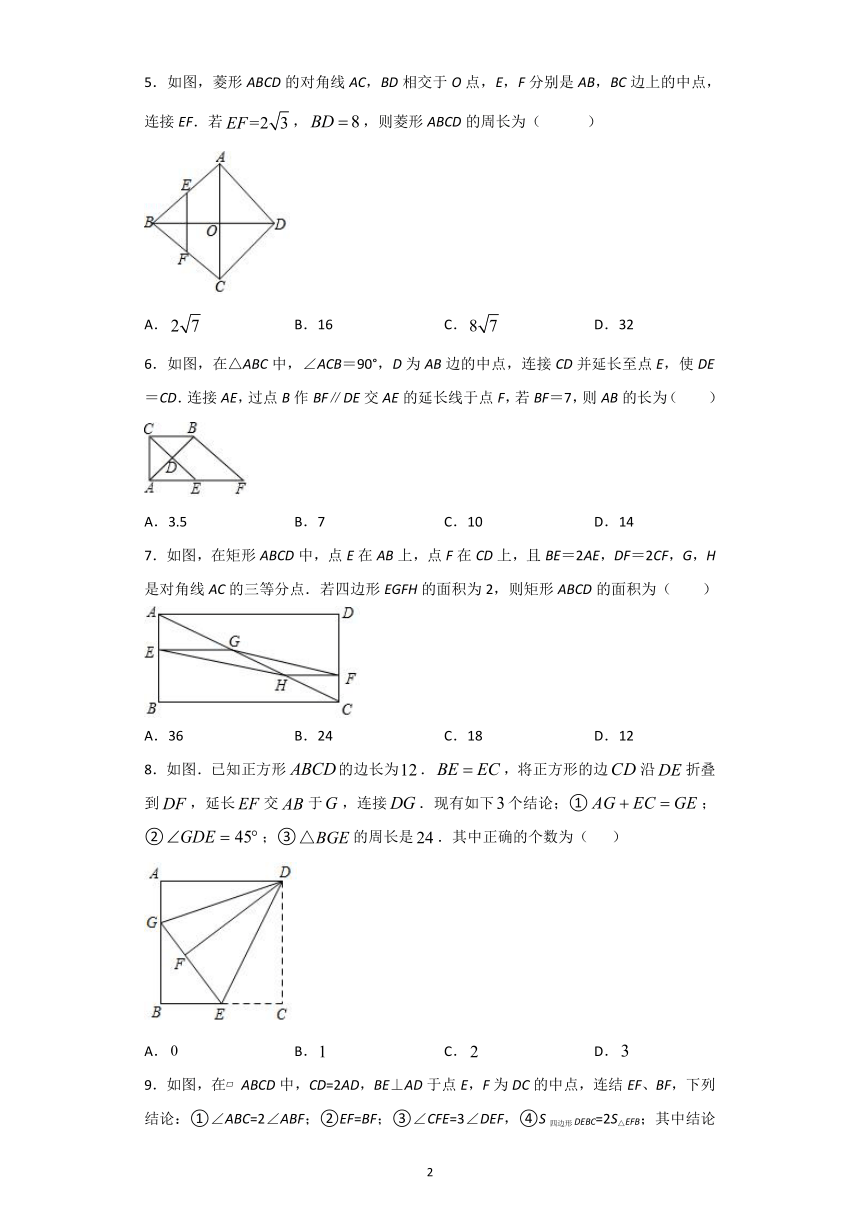
5.如图,菱形ABCD的对角线AC,BD相交于O点,E,F分别是AB,BC边上的中点,连接EF.若,,则菱形ABCD的周长为( )
A. B.16 C. D.32
6.如图,在△ABC中,∠ACB=90°,D为AB边的中点,连接CD并延长至点E,使DE=CD.连接AE,过点B作BF∥DE交AE的延长线于点F,若BF=7,则AB的长为( )
A.3.5 B.7 C.10 D.14
7.如图,在矩形ABCD中,点E在AB上,点F在CD上,且BE=2AE,DF=2CF,G,H是对角线AC的三等分点.若四边形EGFH的面积为2,则矩形ABCD的面积为( )
A.36 B.24 C.18 D.12
8.如图.已知正方形的边长为.,将正方形的边沿折叠到,延长交于,连接.现有如下个结论;①;②;③的周长是.其中正确的个数为( )
A. B. C. D.
9.如图,在?ABCD中,CD=2AD,BE⊥AD于点E,F为DC的中点,连结EF、BF,下列结论:①∠ABC=2∠ABF;②EF=BF;③∠CFE=3∠DEF,④S四边形DEBC=2S△EFB;其中结论正确的个数共有( )
A.1个 B.2个 C.3个 D.4个
10.下列说法正确的有几个()
①两组对角分别相等的四边形是平行四边形;②对角线互相平分的四边形是平行四边形;③对角线相等的平行四边形是矩形;④矩形的四个角是直角;⑤对角线互相垂直的四边形是菱形;⑥对角线互相垂直的平行四边形是菱形;⑦四条边相等的四边形是菱形.
A.6个 B.5个 C.4个 D.7个
11.如图1,E为矩形ABCD边AD上一点,点P从点B沿折线BE→ED→DC,运动到点C 时停止;点Q从点B沿BC运动到点C时停止.它们运动的速度都是1cm/s.若P,Q同时开始运动,设运动时间为t(s),△BPQ的面积为y(cm2).已知y与t的函数图象如图2,则下列结论错误的是( )
A.BE=10cm B.AB=8cm C.AE=6cm D.BC=14cm
二、填空题
12.如图,在边长为2的菱形ABCD中,DE⊥AB于点E,连接CE,若AE=BE,则CE的长是_____.
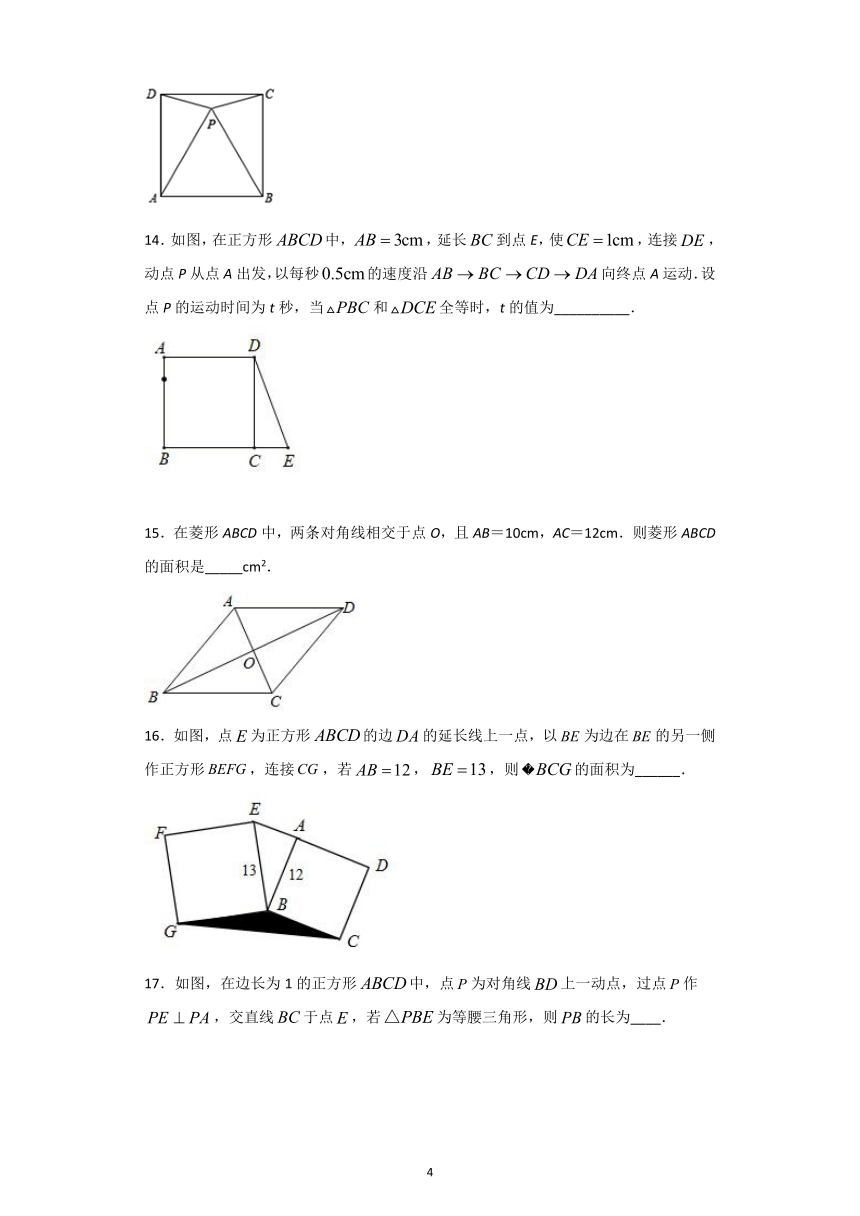
13.已知点P是正方形ABCD内部一点,且是正三角形,则∠CPD=______度.
14.如图,在正方形中,,延长到点E,使,连接,动点P从点A出发,以每秒的速度沿向终点A运动.设点P的运动时间为t秒,当和全等时,t的值为__________.
15.在菱形ABCD中,两条对角线相交于点O,且AB=10cm,AC=12cm.则菱形ABCD的面积是_____cm2.
16.如图,点为正方形的边的延长线上一点,以为边在的另一侧作正方形,连接,若,,则的面积为______.
17.如图,在边长为1的正方形中,点为对角线上一动点,过点作,交直线于点,若为等腰三角形,则的长为____.
三、解答题
18.如图,点E、F、G、H分别在矩形的边、、、(不包括端点),上运动,且满足,.
(1)求证:四边形是平行四边形;
(2)请探究四边形的周长一半与矩形一条对角线长的大小关系,并说明理由.
19.已知:如图,在中,为边上一点,以为邻边作平行四边形,连接.
(1)求证:;
(2)求证:;
(3)当点在什么位置时,四边形是矩形,请说明理由.
20.已知:如图,在中,E为的中点,连接并延长交的延长线于点F,连接.
(1)求证:;
(2)嘉琪说:“添加一个条件,能使四边形是矩形”,你是否同意嘉琪的观点,如果同意,请添加一个条件,并给出证明;如果不同意,请说明理由.
21.如图,为长方形的边上一点,将长方形沿折叠,使点恰好落在上的点处.
(1)求证:;
(2)若,,求的长.
22.如图,在□ABCD中,对角线AC与BD相交于点O,点E,F分别为OB,OD的中点,延长AE至G,使EG=AE,连接CG.
(1)求证:△ABE≌△CDF;
(2)当AB与AC满足什么数量关系时,四边形EGCF是矩形?请说明理由.
23.如图,长方形中,,,现有一动点P从A出发以1/秒的速度,沿矩形的边A—B—C—D—A,设点P的运动时间为t秒.
(1)当秒时,求的面积;
(2)当t为何值时,点P与点A的距离为5?
(3)当t为何值时(),以线段、、的长度构成的三角形是直角三角形,且是斜边.
参考答案
1.A
解:A、对角线互相垂直的平行四边形是菱形,原命题是假命题;
B、正方形的对角线互相垂直平分,是真命题;
C、矩形的对角线相等,是真命题;
D、对角线互相平分的四边形是平行四边形,是真命题;
故选:A.
2.C
【详解】
解:作BM⊥x轴于M.
∵四边形ABCD是正方形,
∴AD=AB,∠DAB=90°,
∴∠DAO+∠BAM=90°,∠BAM+∠ABM=90°,
∴∠DAO=∠ABM,
∵∠AOD=∠AMB=90°,
在△DAO和△ABM中,
,
∴△DAO≌△ABM(AAS),
∴BM=OA,
∵A(,0),B(2,b),
∴BM=OA=3,
∴b=.
故选:C.
3.C
【详解】
解:过M作MP⊥AB于P,交DC于Q,如图所示:
则四边形DEMQ,四边形QMFC,四边形AEMP,四边形MPBF都是矩形,
∴S△DEM=S△DQM,S△QCM=S△MFC,S△AEM=S△APM,S△MPB=S△MFB,S△ABC=S△ADC,
∴S△ABC-S△AMP-S△MCF=S△ADC-S△AEM-S△MQC,
∴S四边形DEMQ=S四边形MPBF,
∵DE=CF=2,
∴S△DEM=S△MFB=×2×4=4,
∴S阴=4+4=8,
4.D
解: 由折叠的性质可知,BE=EH,AF=FG,GH=AB,∠BEF=∠HEF,
∵∠BEF+∠HEF=180°-∠HEC=120°,
∴∠HEF=60°
∵FH∥CE,∠HEC=60°,
∴∠FHE=∠HEC=60°,
∴△HEF为等边三角形,
∴EF=HE=FH,
∵∠FHE=60°,∠B=∠GHE=∠FHE+∠GHF=90°,
∴∠GHF=30°,
在Rt△FGH中,∠GHF=30°,
∴FH=2FG=2AF,
∴设FG=x,则FH=2x,HD=x,
则有,
∴AD=AF+FH+HD=4x,
又∵矩形ABCD的面积为,
∴,
∴x=2或x=-2(舍),
∴EF=FH=4,
故选:D.
5.C
【详解】
解:∵E,F分别是AB,BC边上的中点,EF=,
∴AC=2EF=,
∵四边形ABCD是菱形,,
∴AC⊥BD,OA=AC=,OB=BD=4,
∴AB==,
∴菱形ABCD的周长为:=.
故选:C.
6.B
解:∵D为AB边的中点,
∴AD=BD,
在△BCD和△AED中,
∵,
∴△BCD≌△AED(SAS),
∴∠CBD=∠EAD,
∴BC∥AE,即BC∥EF,
又∵BF∥CE,
∴四边形BCEF是平行四边形,
∴CE=BF=7,
∴CD=CE=3.5,
∴AB=2CD=7,
故选:B.
7.C
【详解】
解:如图,连接AF,CE,
∵四边形ABCD是矩形,
∴S△ABC=S△ADC=S矩形ABCD,
∵BE=2AE,DF=2CF,
∴S△AEC=S△ABC=S矩形ABCD,S△AFC=S△ADC=S矩形ABCD,
∵G,H是对角线AC的三等分点,
∴S△EGH=S△GFH=S矩形ABCD,
∵四边形EGFH的面积为2,
∴S△EGH+S△GFH=2,
∴S矩形ABCD=2,
∴S矩形ABCD=18
故选:C.
8.D
正方形的边CD沿DE折叠到DF,延长EF交AB于G,
∴EF=EC,DF=DC,∠CDE=∠FDE,
∵DA=DF,DG=DG,
∴Rt△ADG≌Rt△FDG,
∴AG=FG,∠ADG=∠FDG,
,故结论①正确;
∴∠GDE=∠FDG+∠FDE
=(∠ADF+∠CDF)
=45°,故结论②正确
∵△BGE的周长=BG+BE+GE,GE=GF+EF=EC+AG,
∴△BGE的周长=BG+BE+ EC+AG
=AB+BC,
正方形ABCD的边长为
的周长为24,故结论③正确;
故选:D
9.D
【详解】
解:如图延长EF交BC的延长线于G,取AB的中点H连接FH.
∵CD=2AD,DF=FC,
∴CF=CB,
∴∠CFB=∠CBF,
∵CD∥AB,
∴∠CFB=∠FBH,
∴∠CBF=∠FBH,
∴∠ABC=2∠ABF.故①正确,
∵DE∥CG,
∴∠D=∠FCG,
∵DF=FC,∠DFE=∠CFG,
∴△DFE≌△CFG(ASA),
∴FE=FG,
∵BE⊥AD,
∴∠AEB=90°,
∵AD∥BC,
∴∠AEB=∠EBG=90°,
∴BF=EF=FG,故②正确,
∵S△DFE=S△CFG,
∴S四边形DEBC=S△EBG=2S△BEF,故④正确,
∵AH=HB,DF=CF,AB=CD,
∴CF=BH,∵CF∥BH,
∴四边形BCFH是平行四边形,
∵CF=BC,
∴四边形BCFH是菱形,
∴∠BFC=∠BFH,
∵FE=FB,FH∥AD,BE⊥AD,
∴FH⊥BE,
∴∠BFH=∠EFH=∠DEF,
∴∠EFC=3∠DEF,故③正确,
故选:D.
10.A
【详解】
解:①两组对角分别相等的四边形是平行四边形,正确,故①符合题意;
②对角线互相平分的四边形是平行四边形,正确,故②符合题意;
③对角线相等的平行四边形是矩形,正确,故③符合题意;
④矩形的四个角是直角,正确,故④符合题意;
⑥对角线互相垂直的平行四边形是菱形,故⑤错误,不符合题意,故⑥正确,符合题意;
⑦四条边相等的四边形是菱形,正确,故⑦符合题意,
故正确的有①②③④⑥⑦,共6个,
故选:A.
11.D
解:由图象可知,BC=BE=10cm,DE=14-10=4cm,
∴AD=10cm,
AE=AD-DE=10-4=6cm,
由勾股定理得,cm
所以,选项A,B,C正确,选项D错误;
故选:D
12.
【详解】
解:连接BD,
∵DE⊥AB,AE=BE,
∴AD=BD,
∵四边形ABCD是菱形,
∴AB=AD=DC=2,AB∥DC,
∴AB=AD=BD,
∴△ABD是等边三角形,
∴∠A=60°,
∴∠ADE=30°,
∴AE=1,DE,
∵DC∥BE,
∴∠CDE=∠AED=90°,
∴CE.
故答案为:.
13.150
解:∵四边形ABCD是正方形,
∴AD=AB=BC,∠DAB=∠ABC=90°,
∵△ABP是等边三角形,
∴AP=BP=AB,∠PAB=∠PBA=60°,
∴AP=AD=BP=BC,∠DAP=∠CBP=30°.
∴∠BCP=∠BPC=∠APD=∠ADP=75°,
∴∠PDC=∠PCD=15°,
∴∠CPD=180°?∠PDC?∠PCD=180°?15°?15°=150°.
故答案为:150.
14.4或14
如图,当≌时,BP1=CE=1
即3-0.5t=1,解得t=4,
如图,当≌时,CP2=CE=1
即0.5t-6=1,解得t=14,
故答案为:4或14.
15.96
【详解】
解:∵四边形ABCD为菱形,
∴AC⊥BD,OA=OC=AC=6cm,OB=OD,
∴OB==8(cm),
∴BD=2OB=16cm,
∴S菱形ABCD=AC?BD=×12×16=96(cm2).
故答案为:96.
16.30
解:如图,延长GB交CD与点H,
∵四边形ABCD是正方形,
∴BA=BC,∠BCH=∠BAE=90°,
∵四边形BEFG是正方形,
∴∠EBG=90°,BE=BG,
∴∠ABE+∠GBC=180°,
又∵∠HBC+∠GBC=180°,
∴∠ABE=∠HBC,
∴△ABE≌△CBH,
∴BH=BE,,
∵BE=BG,
∴BH=BG,
∴,
在Rt△ABE中,,
∵,
∴,
故答案为:30.
17.,
【详解】
解:由正方形的性质可知:,对角线互相垂直且把每组对角都分成了两个45°的角,接下来可分为以下情况讨论:
①如图,当点P与点D重合时,此时点E与点C重合,且满足为等腰三角形,
∴;
②如图,当点P从点D运动到DB中点(不含端点)的过程中时,,
∴
∵
∴为钝角,
∴不是等腰三角形,
∴该情况不成立;
③当P点运动到对角线的交点处时,此时E点与B点重合,不符合题意;
当P点运动到与B点重合时,三角形不存在,即不符合题意;
④如图,当点P从点O运动到点B的过程中时,
∵,
∴,
若为等腰三角形,
则有
∵,
∴
又∵,
∴
∴
∵
∴,
∴,
∴.
综上可得:PB的长为或.
故答案为:或.
18.
(1)∵四边形是矩形,
.
∴在与中,,
,
同理证得,则.
∴四边形是平行四边形;
(2)四边形的周长一半大于或等于矩形一条对角线长度.
理由:如图,作G关于的对称点,连接、、.
则由对称的性质知:,
∴
∵∥,
∴四边形是平行四边形
∴
∵
∴
∴的长度就是的最小值
∵EF+FG是四边形周长的一半
∴四边形的周长一半大于或等于矩形一条对角线长度.
19.
(1)证明:∵AB=AC,
∴∠B=∠2,
又∵四边形ABDE是平行四边形,
∴AB∥DE,
∴∠B=∠1,
∴∠1=∠2;
(2)证明:∵四边形ABDE是平行四边形,
∴AB=ED,
∵AB=AC,
∴AC=ED,
在△ADC和△ECD中,
,
∴△ADC≌△ECD(SAS);
(3)解:点D在BC的中点上时,四边形ADCE是矩形,理由如下:
∵四边形ABDE是平行四边形,
∴AE=BD,AE∥BC,
∵D为边长BC的中点,
∴BD=CD,
∴AE=CD,AE∥CD,
∴四边形ADCE是平行四边形,
∵△ADC≌△ECD,
∴AC=DE,
∴四边形ADCE是矩形.
20.
(1)证明:∵四边形是平行四边形,
.
,
为的中点,
.
,
.
(2)解:答:同意.添加条件是:当时,四边形是矩形.
证明:
∴四边形是平行四边形.
∴四边形是矩形.
21.
解:(1)∵四边形ABCD是长方形,
∴AD=BC,∠A=90°,AB∥CD,
∴∠AED=∠CDF,
∵∠A=∠CFD=90°,由折叠可知:AD=BC=CF,
∴△ADE≌△FCD(AAS),
∴AE=DF;
(2)设CD=x,则AE=x-1,
由折叠得:AD=CF=BC=3,
∵△ADE≌△FCD,
∴ED=CD=x,
Rt△AED中,AE2+AD2=ED2,
∴(x-1)2+32=x2,
∴x=5,
∴CD=5.
22.
解:(1)证明:∵四边形ABCD是平行四边形,
∴AB=CD,AB//CD,OB=OD,OA=OC,
∴∠ABE=∠CDF,
∵点E,F分别为OB,OD的中点,
∴BE=OB,DF=OD,
∴BE=DF,
在△ABE和△CDF中,
,
∴△ABE≌△CDF(SAS);
(2)当AC=2AB时,四边形EGCF是矩形;理由如下:
∵AC=2OA,AC=2AB,
∴AB=OA,
∵E是OB的中点,
∴AG⊥OB,
∴∠OEG=90°,
同理:CF⊥OD,
∴AG//CF,
∴EG//CF,
由(1)得:△ABE≌△CDF,
∴AE=CF,
∵EG=AE,
∴EG=CF,
∴四边形EGCF是平行四边形,
∵∠OEG=90°,
∴四边形EGCF是矩形.
23.
解:(1)当t=6时,点P的路程为1×6=6cm,
∵AB=4cm,BC=6cm,
∴点P在BC上,且,
∴;
(2)①若点P在BC上,
∵在Rt△ABP中,AP=5,AB=4,
∴BP=t﹣4=3,
∴;
②若点P在DC上,
则在Rt△ADP中,AP是斜边,
∵AD=6,
∴AP>6,
∴AP≠5;
③若点P在AD上,
AP=5,
则点P的路程为20﹣5=15,
∴,
综上,当或时,AP=5cm.
(3)当4<t<10时,点P在BC边上,
∵BP=t﹣4,CP=10﹣t,
∴AP2=AB2+BP2=42+(t﹣4)2
由题意,有AD2+CP2=AP2
∴62+(10﹣t)2=42+(t﹣4)2
∴.
一、单选题
1.下列命题中,假命题是( )
A.对角线互相垂直的四边形是菱形
B.正方形的对角线互相垂直平分
C.矩形的对角线相等
D.对角线互相平分的四边形是平行四边形
2.如图,在平面直角坐标系xOy中,正方形ABCD的顶点D在y轴上,且A(﹣3,0),B(2,b),则b的值为( )
A.3 B.2 C.﹣3 D.﹣2
3.矩形中,点M在对角线上,过M作的平行线交于E,交于F,连接和,已知,,则图中阴影部分的面积是( )
A.12 B.10 C.8 D.6
4.如图,在矩形中,点,分别在边和上,把该矩形沿折叠,使点恰好落在边的点处,已知矩形的面积为,,则折痕的长为( )
A. B.2 C. D.4
5.如图,菱形ABCD的对角线AC,BD相交于O点,E,F分别是AB,BC边上的中点,连接EF.若,,则菱形ABCD的周长为( )
A. B.16 C. D.32
6.如图,在△ABC中,∠ACB=90°,D为AB边的中点,连接CD并延长至点E,使DE=CD.连接AE,过点B作BF∥DE交AE的延长线于点F,若BF=7,则AB的长为( )
A.3.5 B.7 C.10 D.14
7.如图,在矩形ABCD中,点E在AB上,点F在CD上,且BE=2AE,DF=2CF,G,H是对角线AC的三等分点.若四边形EGFH的面积为2,则矩形ABCD的面积为( )
A.36 B.24 C.18 D.12
8.如图.已知正方形的边长为.,将正方形的边沿折叠到,延长交于,连接.现有如下个结论;①;②;③的周长是.其中正确的个数为( )
A. B. C. D.
9.如图,在?ABCD中,CD=2AD,BE⊥AD于点E,F为DC的中点,连结EF、BF,下列结论:①∠ABC=2∠ABF;②EF=BF;③∠CFE=3∠DEF,④S四边形DEBC=2S△EFB;其中结论正确的个数共有( )
A.1个 B.2个 C.3个 D.4个
10.下列说法正确的有几个()
①两组对角分别相等的四边形是平行四边形;②对角线互相平分的四边形是平行四边形;③对角线相等的平行四边形是矩形;④矩形的四个角是直角;⑤对角线互相垂直的四边形是菱形;⑥对角线互相垂直的平行四边形是菱形;⑦四条边相等的四边形是菱形.
A.6个 B.5个 C.4个 D.7个
11.如图1,E为矩形ABCD边AD上一点,点P从点B沿折线BE→ED→DC,运动到点C 时停止;点Q从点B沿BC运动到点C时停止.它们运动的速度都是1cm/s.若P,Q同时开始运动,设运动时间为t(s),△BPQ的面积为y(cm2).已知y与t的函数图象如图2,则下列结论错误的是( )
A.BE=10cm B.AB=8cm C.AE=6cm D.BC=14cm
二、填空题
12.如图,在边长为2的菱形ABCD中,DE⊥AB于点E,连接CE,若AE=BE,则CE的长是_____.
13.已知点P是正方形ABCD内部一点,且是正三角形,则∠CPD=______度.
14.如图,在正方形中,,延长到点E,使,连接,动点P从点A出发,以每秒的速度沿向终点A运动.设点P的运动时间为t秒,当和全等时,t的值为__________.
15.在菱形ABCD中,两条对角线相交于点O,且AB=10cm,AC=12cm.则菱形ABCD的面积是_____cm2.
16.如图,点为正方形的边的延长线上一点,以为边在的另一侧作正方形,连接,若,,则的面积为______.
17.如图,在边长为1的正方形中,点为对角线上一动点,过点作,交直线于点,若为等腰三角形,则的长为____.
三、解答题
18.如图,点E、F、G、H分别在矩形的边、、、(不包括端点),上运动,且满足,.
(1)求证:四边形是平行四边形;
(2)请探究四边形的周长一半与矩形一条对角线长的大小关系,并说明理由.
19.已知:如图,在中,为边上一点,以为邻边作平行四边形,连接.
(1)求证:;
(2)求证:;
(3)当点在什么位置时,四边形是矩形,请说明理由.
20.已知:如图,在中,E为的中点,连接并延长交的延长线于点F,连接.
(1)求证:;
(2)嘉琪说:“添加一个条件,能使四边形是矩形”,你是否同意嘉琪的观点,如果同意,请添加一个条件,并给出证明;如果不同意,请说明理由.
21.如图,为长方形的边上一点,将长方形沿折叠,使点恰好落在上的点处.
(1)求证:;
(2)若,,求的长.
22.如图,在□ABCD中,对角线AC与BD相交于点O,点E,F分别为OB,OD的中点,延长AE至G,使EG=AE,连接CG.
(1)求证:△ABE≌△CDF;
(2)当AB与AC满足什么数量关系时,四边形EGCF是矩形?请说明理由.
23.如图,长方形中,,,现有一动点P从A出发以1/秒的速度,沿矩形的边A—B—C—D—A,设点P的运动时间为t秒.
(1)当秒时,求的面积;
(2)当t为何值时,点P与点A的距离为5?
(3)当t为何值时(),以线段、、的长度构成的三角形是直角三角形,且是斜边.
参考答案
1.A
解:A、对角线互相垂直的平行四边形是菱形,原命题是假命题;
B、正方形的对角线互相垂直平分,是真命题;
C、矩形的对角线相等,是真命题;
D、对角线互相平分的四边形是平行四边形,是真命题;
故选:A.
2.C
【详解】
解:作BM⊥x轴于M.
∵四边形ABCD是正方形,
∴AD=AB,∠DAB=90°,
∴∠DAO+∠BAM=90°,∠BAM+∠ABM=90°,
∴∠DAO=∠ABM,
∵∠AOD=∠AMB=90°,
在△DAO和△ABM中,
,
∴△DAO≌△ABM(AAS),
∴BM=OA,
∵A(,0),B(2,b),
∴BM=OA=3,
∴b=.
故选:C.
3.C
【详解】
解:过M作MP⊥AB于P,交DC于Q,如图所示:
则四边形DEMQ,四边形QMFC,四边形AEMP,四边形MPBF都是矩形,
∴S△DEM=S△DQM,S△QCM=S△MFC,S△AEM=S△APM,S△MPB=S△MFB,S△ABC=S△ADC,
∴S△ABC-S△AMP-S△MCF=S△ADC-S△AEM-S△MQC,
∴S四边形DEMQ=S四边形MPBF,
∵DE=CF=2,
∴S△DEM=S△MFB=×2×4=4,
∴S阴=4+4=8,
4.D
解: 由折叠的性质可知,BE=EH,AF=FG,GH=AB,∠BEF=∠HEF,
∵∠BEF+∠HEF=180°-∠HEC=120°,
∴∠HEF=60°
∵FH∥CE,∠HEC=60°,
∴∠FHE=∠HEC=60°,
∴△HEF为等边三角形,
∴EF=HE=FH,
∵∠FHE=60°,∠B=∠GHE=∠FHE+∠GHF=90°,
∴∠GHF=30°,
在Rt△FGH中,∠GHF=30°,
∴FH=2FG=2AF,
∴设FG=x,则FH=2x,HD=x,
则有,
∴AD=AF+FH+HD=4x,
又∵矩形ABCD的面积为,
∴,
∴x=2或x=-2(舍),
∴EF=FH=4,
故选:D.
5.C
【详解】
解:∵E,F分别是AB,BC边上的中点,EF=,
∴AC=2EF=,
∵四边形ABCD是菱形,,
∴AC⊥BD,OA=AC=,OB=BD=4,
∴AB==,
∴菱形ABCD的周长为:=.
故选:C.
6.B
解:∵D为AB边的中点,
∴AD=BD,
在△BCD和△AED中,
∵,
∴△BCD≌△AED(SAS),
∴∠CBD=∠EAD,
∴BC∥AE,即BC∥EF,
又∵BF∥CE,
∴四边形BCEF是平行四边形,
∴CE=BF=7,
∴CD=CE=3.5,
∴AB=2CD=7,
故选:B.
7.C
【详解】
解:如图,连接AF,CE,
∵四边形ABCD是矩形,
∴S△ABC=S△ADC=S矩形ABCD,
∵BE=2AE,DF=2CF,
∴S△AEC=S△ABC=S矩形ABCD,S△AFC=S△ADC=S矩形ABCD,
∵G,H是对角线AC的三等分点,
∴S△EGH=S△GFH=S矩形ABCD,
∵四边形EGFH的面积为2,
∴S△EGH+S△GFH=2,
∴S矩形ABCD=2,
∴S矩形ABCD=18
故选:C.
8.D
正方形的边CD沿DE折叠到DF,延长EF交AB于G,
∴EF=EC,DF=DC,∠CDE=∠FDE,
∵DA=DF,DG=DG,
∴Rt△ADG≌Rt△FDG,
∴AG=FG,∠ADG=∠FDG,
,故结论①正确;
∴∠GDE=∠FDG+∠FDE
=(∠ADF+∠CDF)
=45°,故结论②正确
∵△BGE的周长=BG+BE+GE,GE=GF+EF=EC+AG,
∴△BGE的周长=BG+BE+ EC+AG
=AB+BC,
正方形ABCD的边长为
的周长为24,故结论③正确;
故选:D
9.D
【详解】
解:如图延长EF交BC的延长线于G,取AB的中点H连接FH.
∵CD=2AD,DF=FC,
∴CF=CB,
∴∠CFB=∠CBF,
∵CD∥AB,
∴∠CFB=∠FBH,
∴∠CBF=∠FBH,
∴∠ABC=2∠ABF.故①正确,
∵DE∥CG,
∴∠D=∠FCG,
∵DF=FC,∠DFE=∠CFG,
∴△DFE≌△CFG(ASA),
∴FE=FG,
∵BE⊥AD,
∴∠AEB=90°,
∵AD∥BC,
∴∠AEB=∠EBG=90°,
∴BF=EF=FG,故②正确,
∵S△DFE=S△CFG,
∴S四边形DEBC=S△EBG=2S△BEF,故④正确,
∵AH=HB,DF=CF,AB=CD,
∴CF=BH,∵CF∥BH,
∴四边形BCFH是平行四边形,
∵CF=BC,
∴四边形BCFH是菱形,
∴∠BFC=∠BFH,
∵FE=FB,FH∥AD,BE⊥AD,
∴FH⊥BE,
∴∠BFH=∠EFH=∠DEF,
∴∠EFC=3∠DEF,故③正确,
故选:D.
10.A
【详解】
解:①两组对角分别相等的四边形是平行四边形,正确,故①符合题意;
②对角线互相平分的四边形是平行四边形,正确,故②符合题意;
③对角线相等的平行四边形是矩形,正确,故③符合题意;
④矩形的四个角是直角,正确,故④符合题意;
⑥对角线互相垂直的平行四边形是菱形,故⑤错误,不符合题意,故⑥正确,符合题意;
⑦四条边相等的四边形是菱形,正确,故⑦符合题意,
故正确的有①②③④⑥⑦,共6个,
故选:A.
11.D
解:由图象可知,BC=BE=10cm,DE=14-10=4cm,
∴AD=10cm,
AE=AD-DE=10-4=6cm,
由勾股定理得,cm
所以,选项A,B,C正确,选项D错误;
故选:D
12.
【详解】
解:连接BD,
∵DE⊥AB,AE=BE,
∴AD=BD,
∵四边形ABCD是菱形,
∴AB=AD=DC=2,AB∥DC,
∴AB=AD=BD,
∴△ABD是等边三角形,
∴∠A=60°,
∴∠ADE=30°,
∴AE=1,DE,
∵DC∥BE,
∴∠CDE=∠AED=90°,
∴CE.
故答案为:.
13.150
解:∵四边形ABCD是正方形,
∴AD=AB=BC,∠DAB=∠ABC=90°,
∵△ABP是等边三角形,
∴AP=BP=AB,∠PAB=∠PBA=60°,
∴AP=AD=BP=BC,∠DAP=∠CBP=30°.
∴∠BCP=∠BPC=∠APD=∠ADP=75°,
∴∠PDC=∠PCD=15°,
∴∠CPD=180°?∠PDC?∠PCD=180°?15°?15°=150°.
故答案为:150.
14.4或14
如图,当≌时,BP1=CE=1
即3-0.5t=1,解得t=4,
如图,当≌时,CP2=CE=1
即0.5t-6=1,解得t=14,
故答案为:4或14.
15.96
【详解】
解:∵四边形ABCD为菱形,
∴AC⊥BD,OA=OC=AC=6cm,OB=OD,
∴OB==8(cm),
∴BD=2OB=16cm,
∴S菱形ABCD=AC?BD=×12×16=96(cm2).
故答案为:96.
16.30
解:如图,延长GB交CD与点H,
∵四边形ABCD是正方形,
∴BA=BC,∠BCH=∠BAE=90°,
∵四边形BEFG是正方形,
∴∠EBG=90°,BE=BG,
∴∠ABE+∠GBC=180°,
又∵∠HBC+∠GBC=180°,
∴∠ABE=∠HBC,
∴△ABE≌△CBH,
∴BH=BE,,
∵BE=BG,
∴BH=BG,
∴,
在Rt△ABE中,,
∵,
∴,
故答案为:30.
17.,
【详解】
解:由正方形的性质可知:,对角线互相垂直且把每组对角都分成了两个45°的角,接下来可分为以下情况讨论:
①如图,当点P与点D重合时,此时点E与点C重合,且满足为等腰三角形,
∴;
②如图,当点P从点D运动到DB中点(不含端点)的过程中时,,
∴
∵
∴为钝角,
∴不是等腰三角形,
∴该情况不成立;
③当P点运动到对角线的交点处时,此时E点与B点重合,不符合题意;
当P点运动到与B点重合时,三角形不存在,即不符合题意;
④如图,当点P从点O运动到点B的过程中时,
∵,
∴,
若为等腰三角形,
则有
∵,
∴
又∵,
∴
∴
∵
∴,
∴,
∴.
综上可得:PB的长为或.
故答案为:或.
18.
(1)∵四边形是矩形,
.
∴在与中,,
,
同理证得,则.
∴四边形是平行四边形;
(2)四边形的周长一半大于或等于矩形一条对角线长度.
理由:如图,作G关于的对称点,连接、、.
则由对称的性质知:,
∴
∵∥,
∴四边形是平行四边形
∴
∵
∴
∴的长度就是的最小值
∵EF+FG是四边形周长的一半
∴四边形的周长一半大于或等于矩形一条对角线长度.
19.
(1)证明:∵AB=AC,
∴∠B=∠2,
又∵四边形ABDE是平行四边形,
∴AB∥DE,
∴∠B=∠1,
∴∠1=∠2;
(2)证明:∵四边形ABDE是平行四边形,
∴AB=ED,
∵AB=AC,
∴AC=ED,
在△ADC和△ECD中,
,
∴△ADC≌△ECD(SAS);
(3)解:点D在BC的中点上时,四边形ADCE是矩形,理由如下:
∵四边形ABDE是平行四边形,
∴AE=BD,AE∥BC,
∵D为边长BC的中点,
∴BD=CD,
∴AE=CD,AE∥CD,
∴四边形ADCE是平行四边形,
∵△ADC≌△ECD,
∴AC=DE,
∴四边形ADCE是矩形.
20.
(1)证明:∵四边形是平行四边形,
.
,
为的中点,
.
,
.
(2)解:答:同意.添加条件是:当时,四边形是矩形.
证明:
∴四边形是平行四边形.
∴四边形是矩形.
21.
解:(1)∵四边形ABCD是长方形,
∴AD=BC,∠A=90°,AB∥CD,
∴∠AED=∠CDF,
∵∠A=∠CFD=90°,由折叠可知:AD=BC=CF,
∴△ADE≌△FCD(AAS),
∴AE=DF;
(2)设CD=x,则AE=x-1,
由折叠得:AD=CF=BC=3,
∵△ADE≌△FCD,
∴ED=CD=x,
Rt△AED中,AE2+AD2=ED2,
∴(x-1)2+32=x2,
∴x=5,
∴CD=5.
22.
解:(1)证明:∵四边形ABCD是平行四边形,
∴AB=CD,AB//CD,OB=OD,OA=OC,
∴∠ABE=∠CDF,
∵点E,F分别为OB,OD的中点,
∴BE=OB,DF=OD,
∴BE=DF,
在△ABE和△CDF中,
,
∴△ABE≌△CDF(SAS);
(2)当AC=2AB时,四边形EGCF是矩形;理由如下:
∵AC=2OA,AC=2AB,
∴AB=OA,
∵E是OB的中点,
∴AG⊥OB,
∴∠OEG=90°,
同理:CF⊥OD,
∴AG//CF,
∴EG//CF,
由(1)得:△ABE≌△CDF,
∴AE=CF,
∵EG=AE,
∴EG=CF,
∴四边形EGCF是平行四边形,
∵∠OEG=90°,
∴四边形EGCF是矩形.
23.
解:(1)当t=6时,点P的路程为1×6=6cm,
∵AB=4cm,BC=6cm,
∴点P在BC上,且,
∴;
(2)①若点P在BC上,
∵在Rt△ABP中,AP=5,AB=4,
∴BP=t﹣4=3,
∴;
②若点P在DC上,
则在Rt△ADP中,AP是斜边,
∵AD=6,
∴AP>6,
∴AP≠5;
③若点P在AD上,
AP=5,
则点P的路程为20﹣5=15,
∴,
综上,当或时,AP=5cm.
(3)当4<t<10时,点P在BC边上,
∵BP=t﹣4,CP=10﹣t,
∴AP2=AB2+BP2=42+(t﹣4)2
由题意,有AD2+CP2=AP2
∴62+(10﹣t)2=42+(t﹣4)2
∴.
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
