3.2实数

(共14张PPT)
（1）5的平方根是
（2） 的算术平方根是
（3）什么叫有理数
想一想： 是有理数吗？
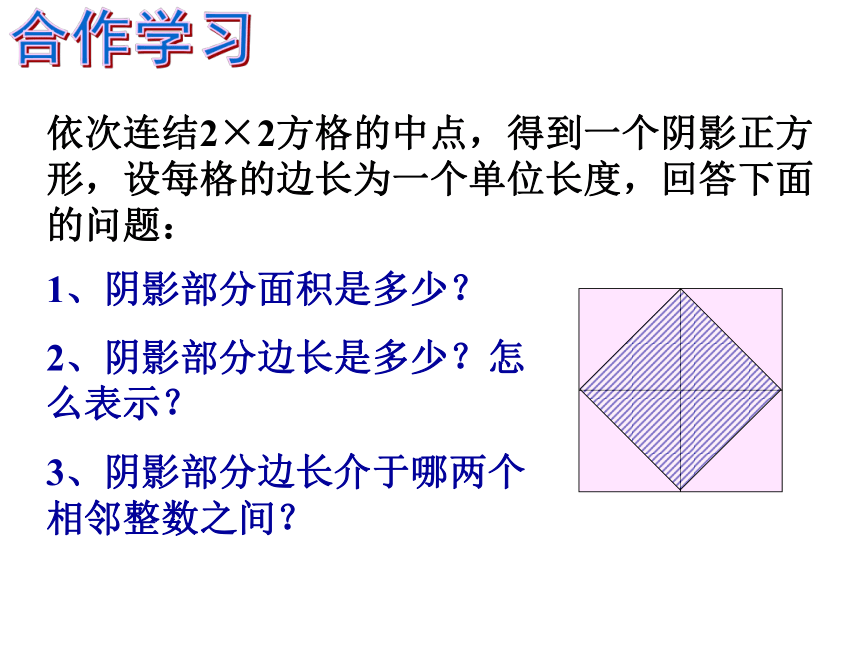
依次连结2×2方格的中点，得到一个阴影正方形，设每格的边长为一个单位长度，回答下面的问题：
1、阴影部分面积是多少？
2、阴影部分边长是多少？怎么表示？
3、阴影部分边长介于哪两个相邻整数之间？
毕达哥拉斯
2500年前
希伯索斯
这是怎样的一类数呢？
是不是有理数？
是不是整数？
是不是分数？
结论： 既不是整数，也不是分数。
所以， 不是有理数。
合作学习：
我们知道， 是介于1和2之间的一个数。请在下列空格处填上适当的不等号。
用这种方法可以得到一系列越来越接近 的近似值。
我们把这种无限不循环小数叫做无理数。
判断下列数哪些是有理数？哪些是无理数？
有理数是：
无理数是：
有理数和无理数统称为实数。
实数
有理数
正有理数
负有理数
零
无理数
正无理数
负无理数
或有理数
整数
分数
（无限不循环小数）
把数从有理数扩充到实数以后，有理数的相反数和绝对值的概念同样适用于实数。
例如： 和 互为相反数
∵
∴绝对值等于 的数是　 和
填空：
（1） 的相反数是__________
（2） 的相反数是
（3） ___________
（4）绝对值等于 的数是 _________
想一想：无理数可以在数轴上表示出来吗？
0
1
-1
在数轴上画
做一做：
在实数范围内，每一个数都可以用数轴上的点来表示；
实数与数轴上的点一一对应
反过来，数轴上的每一个点都表示一个实数。
并且：在数轴上表示的两个实数，右边的数总比左边的数大。
一、判断：
1.实数不是有理数就是无理数。（ ）
2.无理数都是无限不循环小数。（ ）
3.无理数都是无限小数。（ ）
4.带根号的数都是无理数。（ ）
5.无理数一定都带根号。（ ）
6.两个无理数之积不一定是无理数。（ ）
7.两个无理数之和一定是无理数。（ ）
8.数轴上的任何一点都可以表示实数。（ ）
×
×
×