7.5一次函数的简单应用1

(共19张PPT)
7.5一次函数的简单应用(1)
㈣ 设计说明
㈠ 教材分析
㈡ 教法与学法
㈢ 教学程序设计
说课流程
㈠教材分析
⒊ 重点难点分析
⒈　教学内容和地位
⒉ 教学目标
使学生体会到数学来源于生活,应用于生活;认识到数学的重要性和必要性.
知识能力目标：
⑴了解建立一次函数模型的一般步骤，培养学生的总结概括能力.
情感目标：
⑵了解分段函数，学习分类思想.
⑶一次函数与方程、不等式的结合
难点：
重点：
教学关键：
让学生亲自经历探索过程，突出重点
对学生适当的提问和引导，突破难点
建立一次函数模型的基本方法和步骤
分段函数的解析式,及自变量的取值范围
学法：
教法：
教学流程：
创设情境——提出猜想——探索验证
——总结归纳——反馈应用
引导——发现法
鼓励学生动手实践、自主探索、合作交流
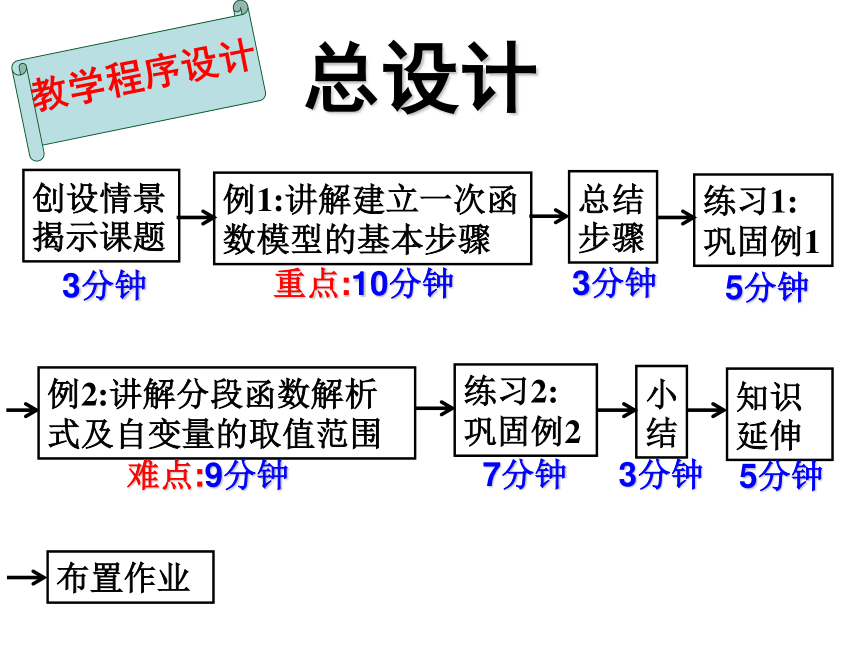
教学程序设计
创设情景揭示课题
例1:讲解建立一次函数模型的基本步骤
总结步骤
练习1:巩固例1
例2:讲解分段函数解析式及自变量的取值范围
练习2:巩固例2
小结
知识延伸
布置作业
3分钟
3分钟
5分钟
难点:9分钟
7分钟
3分钟
5分钟
重点:10分钟
总设计
x
鲸
例1:生物学家测得7条成熟的雄性鲸的全长y和吻尖到喷水孔的长度x的数据如下表（单位：米）：
吻尖到喷水孔的长度x(m ) 1.78 1.91 2.06 2.32 2.59 2.82 2.95
全长y(m) 10.00 10.25 10.72 11.52 12.50 13.16 13.90
突然发现第八条鲸鱼,它的吻尖到喷水孔的长度x =3米,你能知道它的全长y吗
表中的两个变量y和x之间有规律吗
吻尖到喷水孔的长度x(m ) 1.78 1.91 2.06 2.32 2.59 2.82 2.95
全长y(m) 10.00 10.25 10.72 11.52 12.50 13.16 13.90
7.5一次函数的应用(1)
我们可以借助何种工具来探索变量y和x之间的规律
o
1 2 3 4 5
2
4
6
8
10
12
14
16
18
20
Y（m）
X（米）
建立一次函数模型的基本步骤是：
⑴ 通过实验、测量获得足够多的两个变量 的对应值；
⑵ 建立合适的直角坐标系，在坐标系内以各对应值为坐标描点，并用描点法画出函数图象；
⑶ 观察函数图象，判定函数类型
应注意的问题:
⑴ 选取适当的坐标轴刻度
⑶ 得到的函数解析式是近似的
⑵ 挑选位置最佳的两个点
练习1:经实验检测,不同气温下声音传播速度如下表所示
（1）能否用一次函数刻画这两个变量x和y的关系？如果能，写出y关于x的函数解析式。
气温x（℃） 0 5 10 15 20
音速y（米/秒） 331 334 337 340 343
（2）当气温x=22 ℃时，小明看到烟花燃放5秒后才听到声响，那么小明与燃放烟花所在地相距多远。
（3）用恰当的方式表示费用y与路程s之间的关系。
例2:某市出租车计费方法如图所示，请根据图象回答下面的问题：
（1）出租车的起步价是多少元？在多少路程内只收起步价？
（2）起步价里程走完之后，每行驶1km需多少车费？
（4）某外地客人坐出租车游览本市，车费为31元，试求出他乘车的里程。
看终点
看交点
看起点
10 20 30 40 50 60 70
O
t（分）
s（千米）
1
2
练习2:小明上午8:00从家里出发,离家的路程s(千米)和所经过的时间t(分)之间的函数关系如图所示,
⑴ 看图说说小明的故事
⑵小明在来去的途中,离家1km处的时间是几时几分？
我学会了...
使我感受最深的是...
我发现生活中...
我还感到的困惑...
相信你一定行:
老师今天送给你们一棵山毛榉和一棵枫树,山毛榉高2.4m,枫树高0.9m。山毛榉的平均生长速度是每年长高0.15m，枫树的平均生长速度是每年长高0.3m.
问：多少年后枫树和山毛榉一样高？
作业:
作业本§7.5(1)
谢谢！