7.5一次函数的简单应用

(共25张PPT)
浙教版实验教材八年级（上）第七章第五节第一课时
学情分析：
1. 知识起点:学生已经学了一次函数的概念、性质、图像等有关知识，并能熟练地用两点法来求一次函数解析式.
2. 能力起点:学生初步形成用一次函数性质解决实际问题的意识,建立函数模型能力亟待提高.
3. 心理起点:对解决与函数有关的应用型问题还存在着不同程度的困难
教
材
分
析
教
学
策
略
教
学
过
程
教
学
反思
说课设计：
知识储备
后续学习
承
上
本节内容
启
下
一次函数的简单应用
方程、不等式、一次函数的概念、性质、图像
反比例函数 二次函数
一、教材分析之地位和作用分析：
1.知识与技能：
2.过程与方法：
3.情感与态度：
一、教材分析之教学目标分析：
描点法
两点法
函数图象
求解析式
实际数据
识别函数
建模法
概念
性质
图象
一次函数
描点法
两点法
函数图象
求解析式
实际数据
识别函数
建模法
1.体验建模的
发生过程.
2.总结建模的
基本方法.
培养学生应用数学的能力和意识, 合作探究的良好品质.
重点：
难点：
　利用图像取得函数的解析式的基本方法和步骤．
一、教材分析之教学重点与难点分析：
建立函数模型解决实际问题
问题情境
建立模型
解释、应用与拓展
2.学法分析：自主探索 合作学习
1.教法分析：
启发式探究法
二、教材策略之教法学法分析：
创设情境
导出方法
自主探索 形成方法
合作交流 应用方法
课堂小结
升华方法
分层作业
巩固方法
三、教学过程之流程图分析：
方法
方法
方法
方法
方法
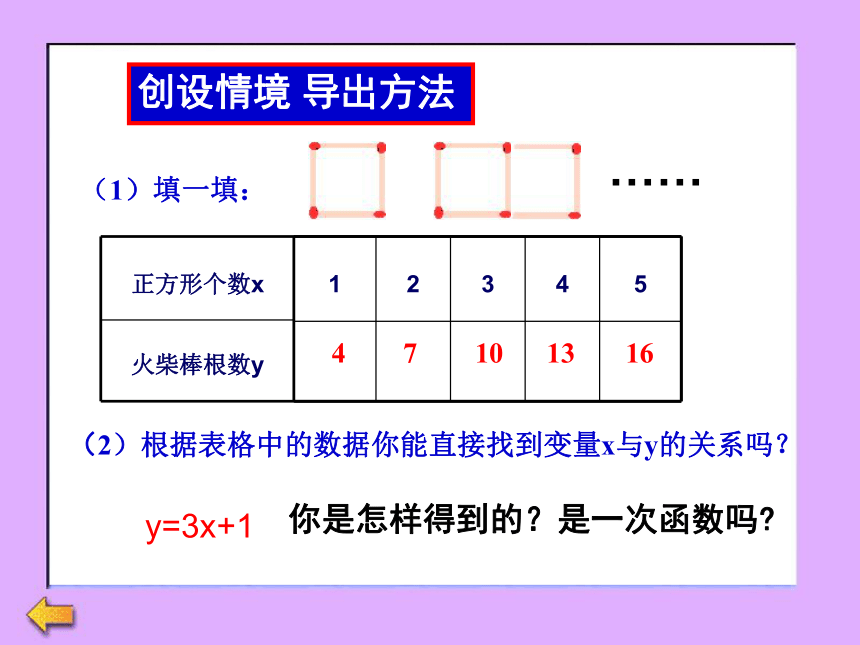
（1）填一填：
正方形个数x
火柴棒根数y
1
2
3
4
5
4
7
10
13
16
……
你是怎样得到的？是一次函数吗
（2）根据表格中的数据你能直接找到变量x与y的关系吗？
y=3x+1
创设情境 导出方法
生物学家测得7条成熟的雄性蓝鲸全长y和吻尖到喷水孔的长度x的数据如下表（单位：m）：
x 1.78 1.91 2.06 2.32 2.59 2.82 2.95
y 10.00 10.25 10.72 11.52 12.50 13.16 13.90
x
蓝鲸
y
（1）根据表格中的数据你能直接找到变量x与y的关系吗？
（2）请你大胆地猜想：变量x与y关系满足怎样的函数关系？
自主探索 形成方法
一次函数
特征
特征
解析式为y=kx+b
图象是一条直线
一次函数
判断
判断
怎样判断“两个变量是否满足一次函数的关系 ”
图象是一条直线
解析式为y=kx+b
生物学家测得7条成熟的雄性蓝鲸全长y和吻尖到喷水孔的长度x的数据如下表（单位：m）：
x 1.78 1.91 2.06 2.32 2.59 2.82 2.95
y 10.00 10.25 10.72 11.52 12.50 13.16 13.90
x
蓝鲸
y
自主探索 形成方法
（1）根据表格中的数据你能直接找到变量x与y的关系吗？
（3）能否利用一次函数刻画这两个变量x和y的关系？
（2）请你大胆地猜想：变量x与y关系满足怎样的函数关系
X（m）
y（m）
0
1
2
3
4
2
4
6
8
10
12
14
16
18
x 1.78 1.91 2.06 2.32 2.59 2.82 2.95
y 10.00 10.25 10.72 11.52 12.50 13.16 13.90
1.建立直角坐标系,描点
2.观察这些点的趋势是否大致在一条直线上,进而判断y是否关于x的一次函数？
3.关系式能求吗？该怎么求？
（3）能否利用一次函数刻画这两个变量x和y的关系？
为我们提供了科学的分析问题方法！
实验数据
画出图像
判断类型
求解析式
数学建模法
自主探索 形成方法
实际生活
解释、解决
练一练
销售额(单位:元)
1月 2月 3月 4月 5月 6月
小李 y1 11600 12800 14000 15200 16400 17600
小张 y2 7400 9200 11000 12800 14600 16400
销售额y
月份x
某公司的销售员小李和小张2007年1到6月的销售额如下表所示：
问：1、试判断小李和小张的销售额y1 、y2与月份x是否满足
一次函数关系式？
2、小李、小张在9月份的销售额各是多少？
如果小李和小张以后每月的销售额都符合上述关系,你是公司销售部经理要从这两名销售员中选一位,你会选谁
3、到2008年8月时小李、小张的销售额各是多少？
合作交流 应用方法
某班同学在探究弹簧的长度跟外力的变化关系时,实验记录得到的相应数据为下表:
砝码的质量x/克 0 50 100 150 200 250 300 350 400
指针位置y/厘米 2 3 4 5 6 7 7.5 7.5 7.5
则y关于x的函数图象为 ( )
y (厘米)
7.5
2
o
x(克)
250
7.5
y (厘米)
2
o
x(克)
300
7.5
y (厘米)
2
o
x(克)
350
y (厘米)
7.5
2
o
x(克)
275
A
B
C
D
小结：应学会观察几个关键点
小明放学骑车回家过程中,时间t与路程s之间的关系如图所示。
0
路程s千米
时间t分钟
5
15
25
1.5
4
(1)根据图象填表:
时间t(分钟) 0 5 15 25
距离s(千米)
(2)请根据图像设计几个问题,并给出解答.
合作交流 应用方法
这节课，
我学会了……
我收获了……
课堂小结
课堂小结 升华方法
1.先识别,再求解析式!
利用一次函数解题时，应先判断是否是一次函数，我们可以从图象或函数的解析式上加以判断，本课中的“蓝鲸问题”就是很好的例子。
2. 读图能力的应用!
后面主要是利用图象获得有用信息，找到刻画两个变量间的变化关系，利用解析式解决实际问题。
建模思想和数形结合的思想
必做题 :1.作业本
2.课本中课内练习、作业题A组
选做题：1.课本中作业题B组
分层作业巩固方法
投影区
课题：7.5 一次函数的简单应用（1）
确定两个变量是一次函数关系的步骤：
教师板演
学生板演
用一次函数解决实际问题的基本步骤：
教学反思
解决问题
知识
情感
过程
体验
经历
掌握
问题
2.设计说明：
(1)突出一个主题:借助函数图像解决实际问题
(2)体现一种方法:两个变量关系不明确时利用函数图像获得经验公式
1.教学设计:始终以问题为主线,以学生掌握函数建模方法为宗旨
(3)渗透一种思想:函数建模思想.
两个变量关系多,
借助图象巧建模,
数形结合更直观,
函数问题易把握.
衷心感谢
各位专家的指导!