二次函数的图像与性质复习

(共19张PPT)
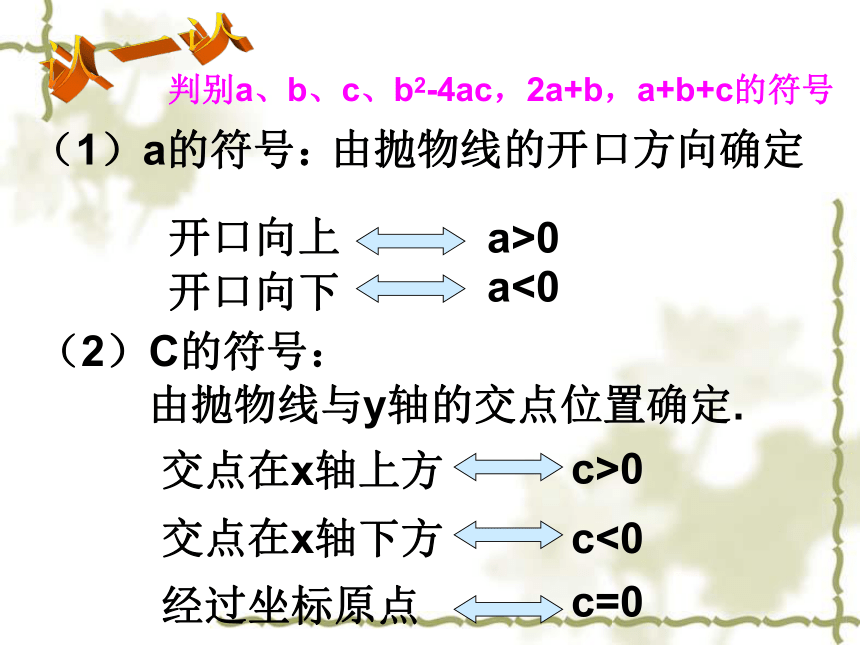
判别a、b、c、b2-4ac，2a+b，a+b+c的符号
（1）a的符号：
由抛物线的开口方向确定
开口向上
a>0
开口向下
a<0
（2）C的符号：
由抛物线与y轴的交点位置确定.
交点在x轴上方
c>0
交点在x轴下方
c<0
经过坐标原点
c=0
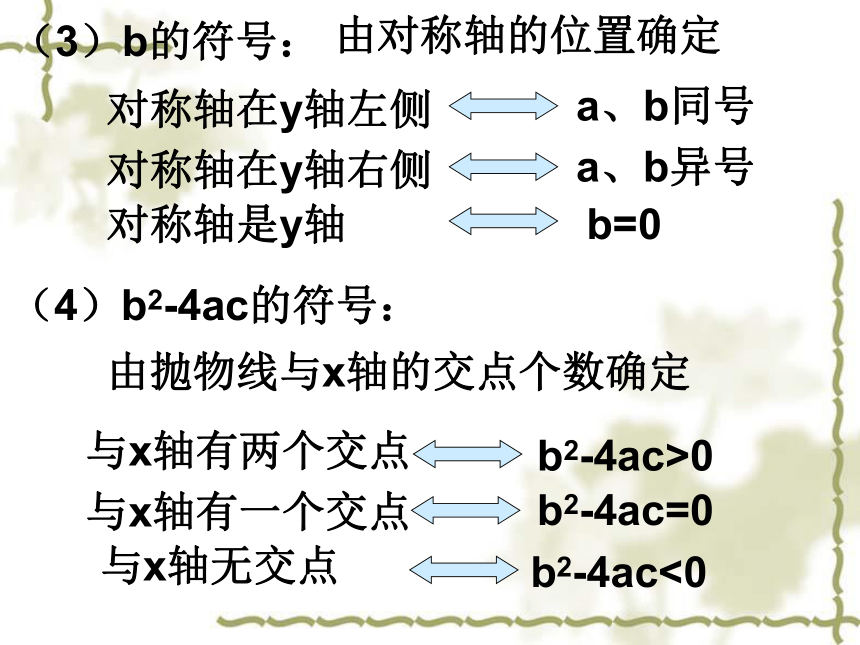
（3）b的符号：
由对称轴的位置确定
对称轴在y轴左侧
a、b同号
对称轴在y轴右侧
a、b异号
对称轴是y轴
b=0
（4）b2-4ac的符号：
由抛物线与x轴的交点个数确定
与x轴有两个交点
b2-4ac>0
与x轴有一个交点
b2-4ac=0
与x轴无交点
b2-4ac<0
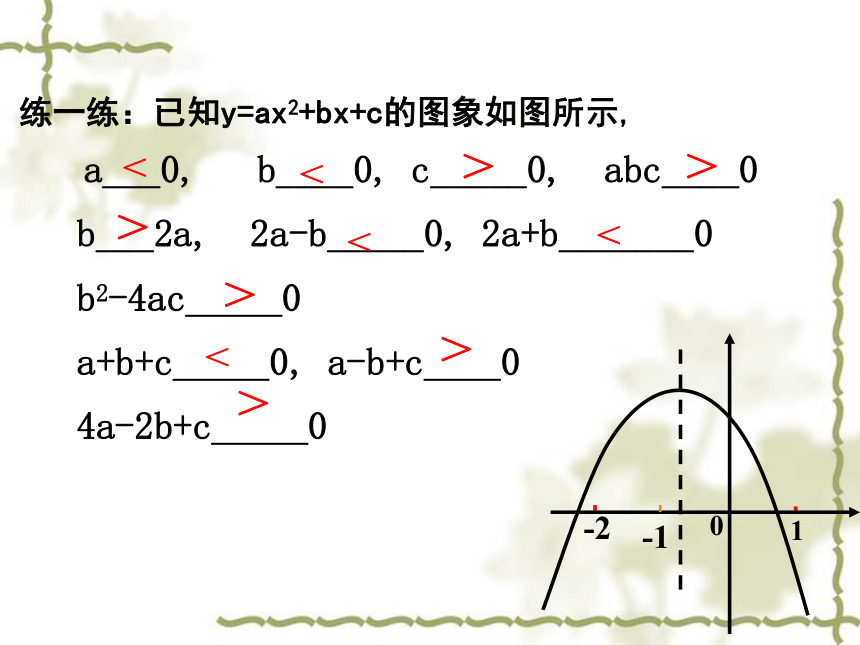
练一练：已知y=ax2+bx+c的图象如图所示,
a___0, b____0, c_____0, abc____0
b___2a, 2a-b_____0, 2a+b_______0
b2-4ac_____0
a+b+c_____0, a-b+c____0
4a-2b+c_____0
0
-1
1
-2
＜
＜
＜
＜
＞
＞
＞
＜
＞
＞
＞
例1：
已知二次函数y=—x2+x-—
（1）求抛物线开口方向，对称轴和顶点M的坐标。
（2）设抛物线与y轴交于C点，与x轴交于A、B两点，求C，
A，B的坐标。
（3）画出函数图象的示意图。
（4）求ΔMAB的周长及面积。
（5）x为何值时，y随的增大而减小，x为何值时，y有最大
（小）值，这个最大（小）值是多少？
（6）x为何值时，y<0？x为何值时，y>0？
1
2
3
2
例1：
已知二次函数y=—x2+x-—
（1）求抛物线开口方向，对称轴和顶点M的坐标。
（2）设抛物线与y轴交于C点，与x轴交于A、B两点，求C，
A，B的坐标。
（3）画出函数图象的示意图。
（4）求ΔMAB的周长及面积。
（5）x为何值时，y随的增大而减小，x为何值时，y有最大
（小）值，这个最大（小）值是多少？
（6）x为何值时，y<0？x为何值时，y>0？
1
2
3
2
解:（1）∵a= —>0
∴抛物线的开口向上
∵y= — (x2+2x+1)-2=—(x+1)2-2
∴对称轴x=-1，顶点坐标M（-1，-2）
1
2
1
2
1
2
例1：
已知二次函数y=—x2+x-—
（1）求抛物线开口方向，对称轴和顶点M的坐标。
（2）设抛物线与y轴交于C点，与x轴交于A、B两点，求C，
A，B的坐标。
（3）画出函数图象的示意图。
（4）求ΔMAB的周长及面积。
（5）x为何值时，y随的增大而减小，x为何值时，y有最大
（小）值，这个最大（小）值是多少？
（6）x为何值时，y<0？x为何值时，y>0？
1
2
3
2
解:
(2)由x=0，得y= - -—
抛物线与y轴的交点C（0，- -—）
由y=0，得—x2+x- —=0
x1=-3 x2=1
与x轴交点A（-3，0）B（1，0）
3
2
3
2
3
2
1
2
例1：
已知二次函数y=—x2+x-—
（1）求抛物线开口方向，对称轴和顶点M的坐标。
（2）设抛物线与y轴交于C点，与x轴交于A、B两点，求C，
A，B的坐标。
（3）画出函数图象的示意图。
（4）求ΔMAB的周长及面积。
（5）x为何值时，y随的增大而减小，x为何值时，y有最大
（小）值，这个最大（小）值是多少？
（6）x为何值时，y<0？x为何值时，y>0？
1
2
3
2
解
0
x
y
(3)
④连线
①画对称轴
x=-1
②确定顶点

(-1,-2)


(0,-–)
③确定与坐标轴的交点
及对称点


(-3,0)
(1,0)
3
2
例1：
已知二次函数y=—x2+x-—
（1）求抛物线开口方向，对称轴和顶点M的坐标。
（2）设抛物线与y轴交于C点，与x轴交于A、B两点，求C，
A，B的坐标。
（3）画出函数图象的示意图。
（4）求ΔMAB的周长及面积。
（5）x为何值时，y随的增大而减小，x为何值时，y有最大
（小）值，这个最大（小）值是多少？
（6）x为何值时，y<0？x为何值时，y>0？
1
2
3
2
解
0

M(-1,-2)


C(0,-–)


A(-3,0)
B(1,0)
3
2
y
x
D
：（4）由对称性可知
MA=MB=√22+22=2√2
AB=|x1-x2|=4
∴ ΔMAB的周长=2MA+AB
=2 √2×2+4=4 √2+4
ΔMAB的面积=—AB×MD
=—×4×2=4
1
2
1
2
例1：
已知二次函数y=—x2+x-—
（1）求抛物线开口方向，对称轴和顶点M的坐标。
（2）设抛物线与y轴交于C点，与x轴交于A、B两点，求C，
A，B的坐标。
（3）画出函数图象的示意图。
（4）求ΔMAB的周长及面积。
（5）x为何值时，y随的增大而减小，x为何值时，y有最大
（小）值，这个最大（小）值是多少？
（6）x为何值时，y<0？x为何值时，y>0？
1
2
3
2
解
解
0
x
x=-1


(0,-–)


(-3,0)
(1,0)
3
2
:(5)

(-1,-2)
当x=-1时，y有最小值为
y最小值=-2
当x≤-1时，y随x的增大
而减小;
例1：
已知二次函数y=—x2+x-—
（1）求抛物线开口方向，对称轴和顶点M的坐标。
（2）设抛物线与y轴交于C点，与x轴交于A、B两点，求C，
A，B的坐标。
（3）画出函数图象的示意图。
（4）求ΔMAB的周长及面积。
（5）x为何值时，y随的增大而减小，x为何值时，y有最大
（小）值，这个最大（小）值是多少？
（6）x为何值时，y<0？x为何值时，y>0？
1
2
3
2
解:
0

(-1,-2)


(0,-–)


(-3,0)
(1,0)
3
2
y
x
由图象可知
(6)
当x< -3或x>1时，y > 0
当-3 < x < 1时，y < 0
返回
抛物线与四边形
例2.如图，已知二次函数图象的顶点坐标为C（1，0），直线y=x+m与该二次函数的图象交于A、B两点，其中A点的坐标为（3，4），B点在Y轴上．
（1）求m的值及这个二次函数的关系式；
（2）P为线段AB上的一个动点（点P与A、B不重合），过P作x轴的垂线与这个二次函数的图象交于点E点，设线段PE的长为h，点P的横坐标为x，求h与x之间的函数关系式，并写出自变量x的取值范围；
（3）D为直线AB与这个二次函数图象对称轴的交点，在线段AB上是否存在一点P，使得四边形DCEP是平行四形？若存在，请求出此时P点的坐标；若不存在，请说明理由．
1.如图，抛物线 与 x轴交于A、B两点，与y轴交于点C。
C
A
B
（3）点P是对称轴上的一点，使PA+PC的值最小，
求点P的坐标 ；
（2）点F、G分别是x轴上和抛物线上的点，使点A、C、 F、G构成平行四边形，
求点F的坐标。
分类讨论思想
p
（1）求A，B，C点的坐标 ；
y
x
0
2
-3
1，小明从右边的二次函数y＝ax2＋bx＋c的图象观察得出下面的五条信息：① a＜ 0；② c＝0；③ 函数的最小值为-3； ④当x＜0时，y>0； ⑤当0＜x1＜x2＜2时，y1 > y2 你认为其中正确的个数有（ ）
A．2 B．3
C．4 D．5
C
小结 回顾
回顾一下，你今天收获了什么？
生活是数学的源泉
思想方法是数学的生命线