4.5三角形的中位线-2020-2021学年浙教版八年级数学下册同步提升训练(Word版含解析)
文档属性
| 名称 | 4.5三角形的中位线-2020-2021学年浙教版八年级数学下册同步提升训练(Word版含解析) |
|
|
| 格式 | doc | ||
| 文件大小 | 358.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-08 00:00:00 | ||
图片预览


文档简介
2020-2021年度浙教版八年级数学下册《4.5三角形的中位线》同步提升训练(附答案)
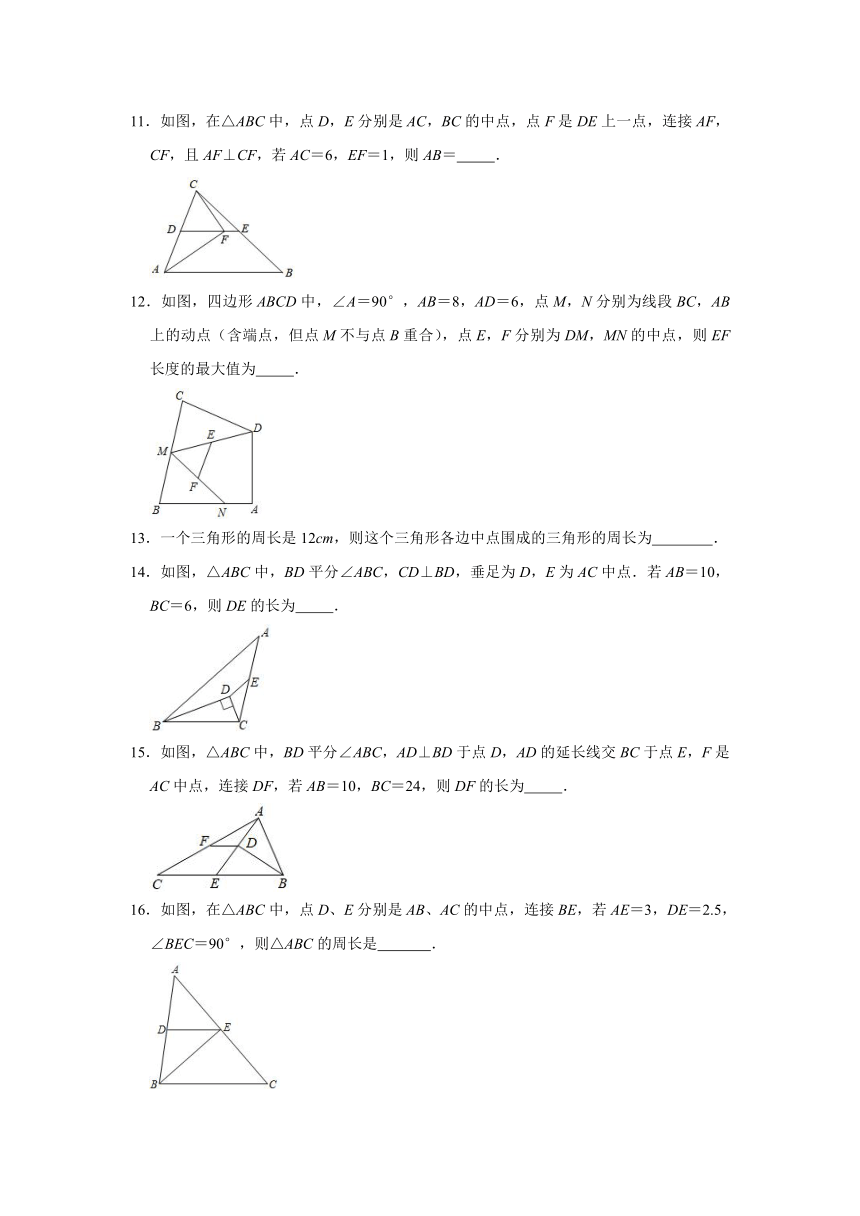
1.如图,△ABC中,AB>AC,AE平分∠BAC,BD⊥AE于D,CE⊥AE于E,F为BC的中点,给出结论:①FD∥AC;②FE=FD;③AB﹣AC=DE;④∠BAC+∠DFE=180°.其中正确的是( )
A.①② B.①②③ C.①②④ D.①②③④
2.如图,四边形ABCD中,AB=1,CD=4,M、N分别是AD、BC的中点,则线段MN的取值范围是( )
A.3<MN<5 B.3<MN≤5 C.<MN< D.<MN≤
如图,已知△ABC中,AB=AC,AD是∠BAC的平分线,AE是∠BAC的外角平分线,ED∥AB交AC于点G,下列结论:①AD⊥BC;②AE∥BC;③AE=AG;
④AD2+AE2=4AG2.其中正确结论的个数是( )
A.1 B.2 C.3 D.4
4.如图,在△ABC中,∠C=90°,AB=13,AC=5,D、E分别是AC、AB的中点,则DE的长是( )
A.6.5 B.6 C.5.5 D.
5.△ABC中,AB=7,BC=6,AC=5,点D、E、F分别是三边的中点,则△DEF的周长为( )A.4.5 B.9 C.10 D.12
6.已知等腰三角形的两条中位线的长分别为3和5,则此等腰三角形的周长为( )
A.22 B.26 C.22或26 D.13
7.如图,平行四边形ABCD中,对角线AC、BD交于点O,点E是BC的中点.若OE=3cm,则AB的长为( )
A.3cm B.6cm C.9cm D.12cm
8.如图,BD、CE是△ABC的中线,P、Q分别是BD、CE的中点,则PQ:BC等于( )
A.1:4 B.1:5 C.1:6 D.1:7
9.如图,四边形ABCD中,AB=BC,F为CD的中点,BE为∠ABC的角平分线,过点A作AE⊥BE于点E,连接EF,若AD=4,则EF的长为( )
A.1.5 B. C.2 D.
10.如图,BD为△ABC的中线,E为BD的中点,连接AE并延长交BC于点F,若BC的长为7,则BF的长为( )
A. B. C. D.
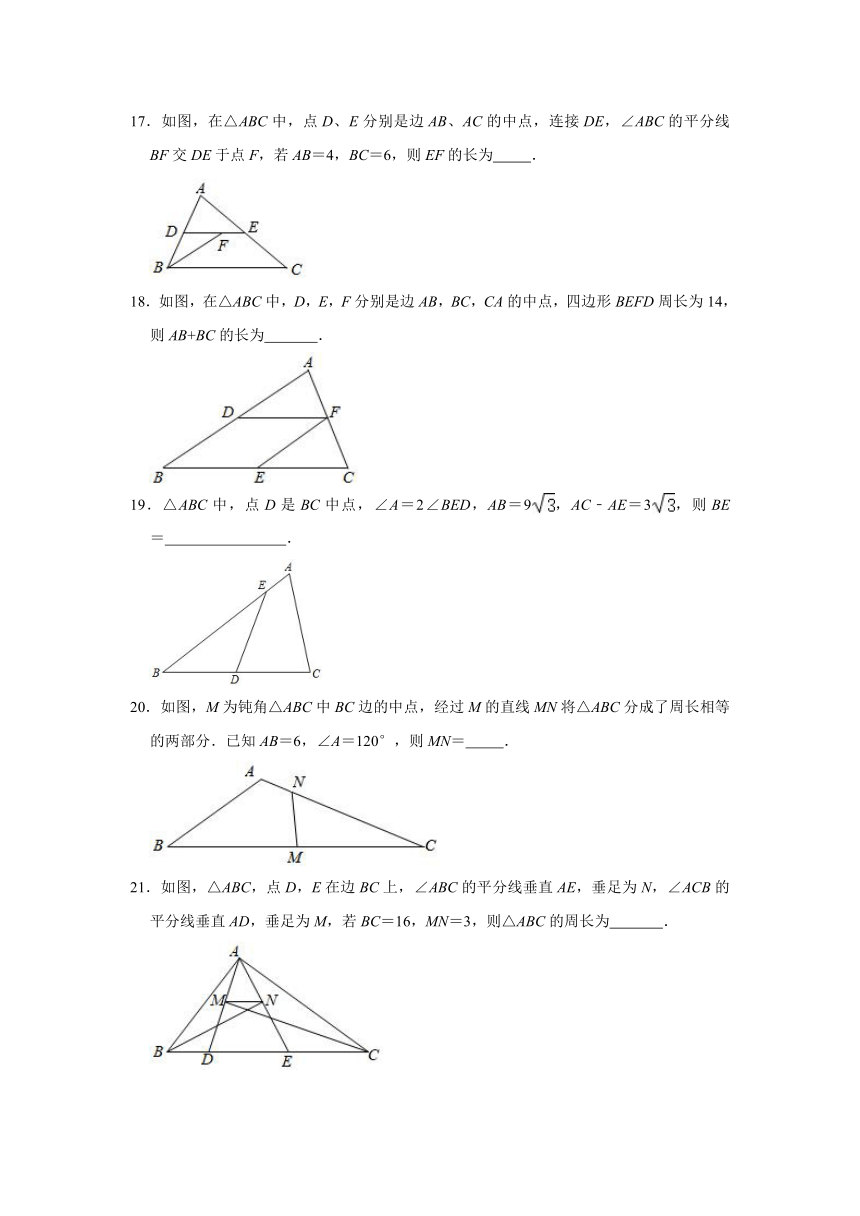
11.如图,在△ABC中,点D,E分别是AC,BC的中点,点F是DE上一点,连接AF,CF,且AF⊥CF,若AC=6,EF=1,则AB= .
12.如图,四边形ABCD中,∠A=90°,AB=8,AD=6,点M,N分别为线段BC,AB上的动点(含端点,但点M不与点B重合),点E,F分别为DM,MN的中点,则EF长度的最大值为 .
13.一个三角形的周长是12cm,则这个三角形各边中点围成的三角形的周长为 .
14.如图,△ABC中,BD平分∠ABC,CD⊥BD,垂足为D,E为AC中点.若AB=10,BC=6,则DE的长为 .
15.如图,△ABC中,BD平分∠ABC,AD⊥BD于点D,AD的延长线交BC于点E,F是AC中点,连接DF,若AB=10,BC=24,则DF的长为 .
16.如图,在△ABC中,点D、E分别是AB、AC的中点,连接BE,若AE=3,DE=2.5,∠BEC=90°,则△ABC的周长是 .
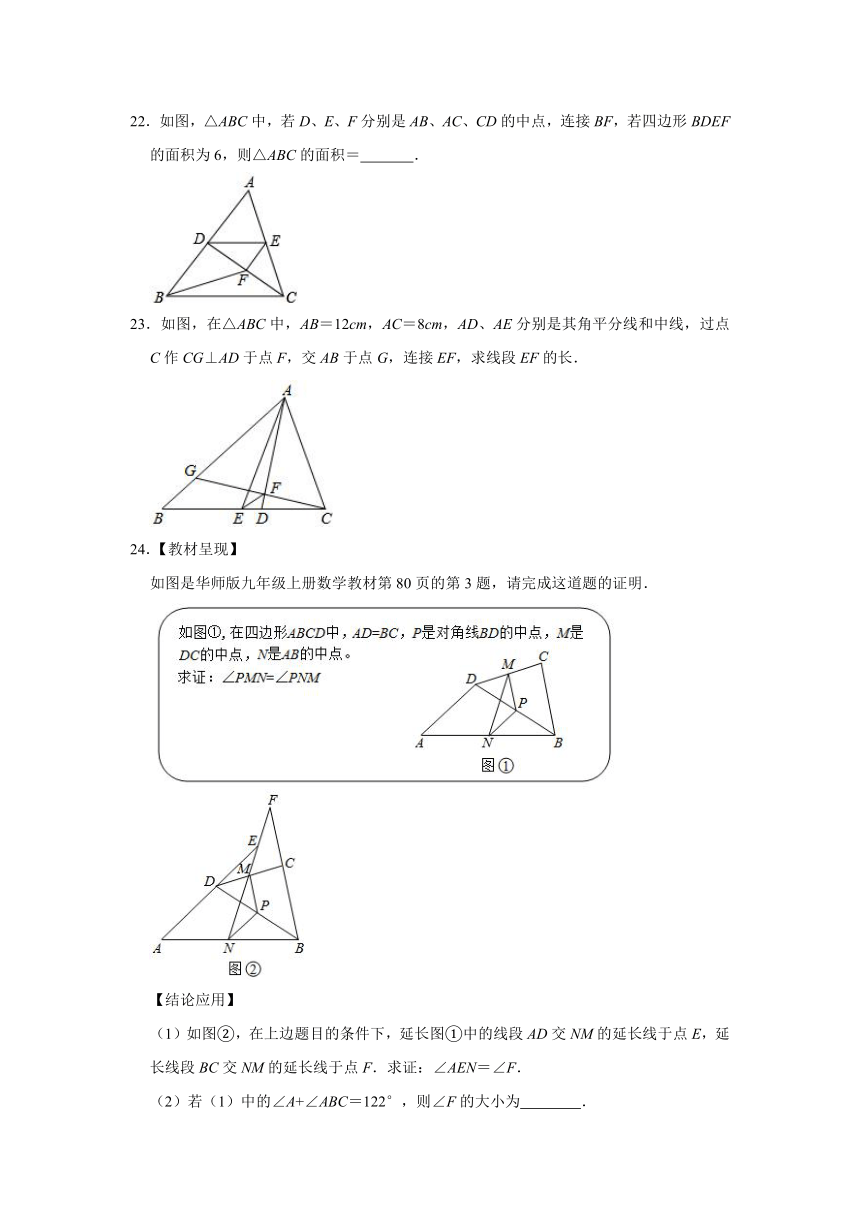
17.如图,在△ABC中,点D、E分别是边AB、AC的中点,连接DE,∠ABC的平分线BF交DE于点F,若AB=4,BC=6,则EF的长为 .
18.如图,在△ABC中,D,E,F分别是边AB,BC,CA的中点,四边形BEFD周长为14,则AB+BC的长为 .
19.△ABC中,点D是BC中点,∠A=2∠BED,AB=9,AC﹣AE=3,则BE= .
20.如图,M为钝角△ABC中BC边的中点,经过M的直线MN将△ABC分成了周长相等的两部分.已知AB=6,∠A=120°,则MN= .
21.如图,△ABC,点D,E在边BC上,∠ABC的平分线垂直AE,垂足为N,∠ACB的平分线垂直AD,垂足为M,若BC=16,MN=3,则△ABC的周长为 .
22.如图,△ABC中,若D、E、F分别是AB、AC、CD的中点,连接BF,若四边形BDEF的面积为6,则△ABC的面积= .
23.如图,在△ABC中,AB=12cm,AC=8cm,AD、AE分别是其角平分线和中线,过点C作CG⊥AD于点F,交AB于点G,连接EF,求线段EF的长.
24.【教材呈现】
如图是华师版九年级上册数学教材第80页的第3题,请完成这道题的证明.
【结论应用】
(1)如图②,在上边题目的条件下,延长图①中的线段AD交NM的延长线于点E,延长线段BC交NM的延长线于点F.求证:∠AEN=∠F.
(2)若(1)中的∠A+∠ABC=122°,则∠F的大小为 .
25.如图,△ABC中,AD平分∠BAC,AD⊥BD,E为BC的中点.
(1)求证:DE∥AC;
(2)若AB=4,AC=6,求DE的长.
26.已知:△ABC中,D是BC上的一点,E、F、G、H分别是BD、BC、AC、AD的中点,
求证:EG、HF互相平分.
27.一个对角线相等的四边形ABCD,E、F分别为AB,CD的中点,EF分别交对角线BD,AC于M,N,求证:△OMN是等腰三角形.
28.如图,在四边形ABCD中,P是对角线BD的中点,E、F分别是AB、CD的中点,AD=BC,∠PEF=20°,求∠PFE的度数.
29.如图,在四边形ABCD中,对角线AC=BD,E,F为AB、CD的中点,连接EF交BD、AC于P、Q,取BC中点G,连EG、FG,求证:OP=OQ.
30.如图,在△ABC中,AB=AC,点D是边AB的中点,DE∥BC交AC于点E,连接BE,点F、G、H分别为BE、DE、BC的中点.
(1)求证:FG=FH;
(2)当∠A为多少度时,FG⊥FH?并说明理由.
参考答案
1.解:延长CE交AB于G,延长BD交AC延长线于H,
∵AE平分∠GAC,AE⊥GC,
∴AG=AC,GE=CE,
同理可得,AB=AH,BD=HD,
∵BF=CF,BD=HD,
∴DF∥CH,即DF∥AC,故①正确,
∴DF=CH,
∵GE=CE,BF=CF,
∴EF=BG,
∵GB=AB﹣AG=AH﹣AC=CH,即GB=CH,
∴GB=CH,即EF=DF,故②正确,
∴AB﹣AC=AB﹣AG=BG,
过G作GI⊥BH于I,
∵∠GED=∠EDI=∠GID=90°,
∴四边形GIDE是矩形,
∴GI=ED,
∴BG>GI=ED,
∴AB﹣AC>DE,故③错误;
∵EF∥BG,DF∥HC,
∴∠FED=∠BAD,∠FDE=∠HAD,
∴∠FED+∠FDE=∠BAD+∠HAD=∠BAC,
∵∠FED+∠FDE+∠EFD=180°,
∴∠BAC+∠EFD=180°,故④正确;
故选:C.
2.解:连接AC,取AC的中点H,连接MH、NH,
∵M、H分别是AD、AC的中点,
∴MH=CD=2,
同理可得,NH=AB=,
在△MHN中,MH﹣NH<MN<MH+NH,即<MN<,
当点H在MN上时,MN=MH+NH=,
∴<MN≤,
故选:D.
3.解:连接EC,
∵AB=AC,AD是∠BAC的平分线,
∴AD⊥BC,故①正确;
∵AB=AC,
∴∠B=∠ACB,
∵AE平分∠FAC,
∴∠FAC=2∠FAE,
∵∠FAC=∠B+∠ACB,
∴∠FAE=∠B,
∴AE∥BC,故②正确;
∵AE∥BC,DE∥AB,
∴四边形ABDE是平行四边形,
∴AE=BD,
∵AB=AC,AD⊥BC,
∴CD=BD,
∴AE=CD,
∵AE∥BC,∠ADC=90°,
∴四边形ADCE是矩形,
∴AC=DE,AG=CG,DG=EG,
∴DG=AG=CG=EG,
在Rt△AED中,AD2+AE2=DE2=AC2=(2AG)2=4AG2,故④正确;
∵AE=BD=BC,AG=AC,
∴AG=AE错误(已知没有条件AC=BC),故③错误;
即正确的个数是3个,
故选:C.
4.解:在△ABC中,∠C=90°,AB=13,AC=5,
则BC===12,
∵D、E分别是AC、AB的中点,
∴DE=BC=6,
故选:B.
5.解:∵点D、E、F分别是三边的中点,
∴DE、EF、DF为△ABC的中位线,
∴DE=AB=×7=,DF=AC=×5=,EF=BC=×6=3,
∴△DEF的周长=++3=9,
故选:B.
6.解:等腰三角形的两条中位线长分别为3和5,
根据三角形中位线定理可知,等腰三角形的两边长为6和10,
当腰为10时,则三边长为10,10,6时,周长为26;
当腰为6时,则三边长为6,6,10时,周长为22,
故选:C.
7.解:∵四边形ABCD是平行四边形,
∴OA=OC;
又∵点E是BC的中点,
∴BE=CE,
∴AB=2OE=2×3=6(cm)
故选:B.
8.解:连接DE,连接并延长EP交BC于点F,
∵DE是△ABC中位线,
∴DE=BC,AE=BE,AD=CD,
∴∠EDB=∠DBF,
∵P、Q是BD、CE的中点,
∴DP=BP,
∵在△DEP与△BFP中,
,
∴△DEP≌△BFP(ASA),
∴BF=DE=BC,P是EF中点,
∴FC=BC,
PQ是△EFC中位线,
PQ=FC,
∴PQ:BC=1:4.
故选:A.
9.解:连接CE,
∵AE⊥BE,
∴∠BEA=90°,
∵BE为∠ABC的角平分线,
∴∠ABE=∠CBE,
在△ABE和△CBE中,
,
∴△ABE≌△CBE(SAS),
∴AE=CE,∠BEC=∠BEA=90°,
∴∠AEC=∠BEC+∠BEA=180°,
∴A,E,C共线,
∵F为CD的中点,
∴EF是△ACD的中位线,
∴EF=AD=×4=2,
故选:C.
10.解:取FC的中点H,连接DH,
∵CD=DA,
∴DH是△ACF的中位线,
∴DH∥AF,
∵BE=ED,
∴BF=FH,
∴BF=FH=HC=BC=,
故选:A.
11.解:在Rt△AFC中,点D是AC的中点,AC=6,
∴DF=AC=×6=3,
∵EF=1,
∴DE=DF+EF=3+1=4,
∵点D,E分别是AC,BC的中点,
∴DE是△ABC的中位线,
∴AB=2DE=2×4=8,
故答案为:8.
12.解:连接DN,
∵点E,F分别为DM,MN的中点,
∴EF是△MND的中位线,
∴EF=DN,
当点N与点B重合时,DN最大,此时DN==10,
∴EF长度的最大值为5,
故答案为:5.
13.解:根据题意,画出图形如图示,
∵点D、E、F分别是AB、AC、BC的中点,
∴DE、DF、EF都是△ABC的中位线,
∴DE=BC,DF=AC,EF=AB,
∵△ABC的周长是12cm,
∴AB+CB+AC=12cm,
∴DE+DF+FE=24÷2=6(cm).
故答案是:6cm.
14.解:延长CD交AB于F,
在△BDC和△BDF中,
,
∴△BDC≌△BDF(ASA),
∴BF=BC=6,CD=DF,
∴AF=AB﹣BF=4,
∵CD=DF,CE=EA,
∴DE=AF=2,
故答案为:2.
15.解:在△ADB和△EDB中,
,
∴△ADB≌△EDB(ASA),
∴EB=AB=10,AD=DE,
∵BC=24,
∴CE=BC﹣BE=14,
∵AF=FC,AD=DE,
∴DF=CE=7,
故答案为:7.
16.解:∵点D、E分别是AB、AC的中点,DE=2.5,
∴BC=2DE=5,
∵E是AC的中点,BE⊥AC,
∴EC=AE=3,BA=BC=5,
∴AC=AE+EC=6,
∴△ABC的周长=BA+BC+AC=16,
故答案为:16.
17.解:连接AF并延长交BC于H,
∵点D、E分别为边AB、AC的中点,
∴DE∥BC,DE=BC=3,AF=FH,
在△BFA和△BFH中,
,
∴△BFA≌△BFH(AAS),
∴BH=AB=4,
∵AD=DB,AF=FH,
∴DF=BH=2,
∴EF=DE﹣DF=1,
故答案为:1.
18.解:∵D,E,F分别是边AB,BC,CA的中点,
∴DF∥BC,EF∥AB,DF=BC,EF=AB,
∴四边形BEFD为平行四边形,
∵四边形BEFD周长为14,
∴DF+EF=7,
∴AB+BC=14.
故答案为14.
19.解:过点D作DF∥AC,交AB于F,
∵点D是BC中点,
∴DF=AC,DF∥AC,BF=AF=AB=,
∴∠BFD=∠A,
∵∠A=2∠BED,∠BFD=∠BED+∠EDF,
∴∠EDF=∠BED,
∴FE=FD,
∵AC﹣AE=3,
∴AE=AC﹣3=2FE﹣3,
∴FE+2FE﹣3=,
解得,FE=,
∴BE=BF+FE=7,
故答案为:7.
20.解:如图,延长CA到D,使AD=AB,连接BD.
∵∠BAC=120°,
∴∠BAD=180°﹣∠BAC=60°,
∴△ABD是等边三角形,
∴BD=AB=AD=6.
∵M为钝角△ABC中BC边的中点,经过M的直线MN将△ABC分成了周长相等的两部分,
∴BM=CM,BM+AB+AN=CM+CN,
∴AB+AN=CN,
∴AD+AN=CN,即DN=CN,
∵BM=CM,
∴MN是△BCD的中位线,
∴MN=BD=3.
故答案为:3.
21.解:在△BNA和△BNE中,
,
∴△BNA≌△BNE(ASA),
∴BE=BA,AN=NE,
同理,CD=CA,AM=MD,
∵AM=MD,AN=NE,MN=3,
∴DE=2MN=6,
∵BE+CD﹣BC=DE,
∴AB+AC=BC+DE=22,
∴△ABC的周长=AB+AC+BC=22+16=38,
故答案为:38.
22.解:∵点F是CD的中点,
∴S△DEF=S△CEF,
设S△DEF=S△CEF=x,
∵D、E分别是AB、AC的中点,
∴S△ADE=S△CDE=2x,S△BDC=S△ADC=4x,S△BDF=2x,
∴S 四边形BDEF=3x.
∵S 四边形BDEF=6,
∴3x=6,
∴x=2,
∴S△ABC=2S△BDC=8x=16,
故答案为:16.
23.解:在△AGF和△ACF中,
,
∴△AGF≌△ACF(ASA).
∴AG=AC=8cm,
∴GF=CF,则BG=AB﹣AG=12﹣8=4(cm).
又∵BE=CE,
∴EF是△BCG的中位线.
∴EF=BG=2cm.
答:EF的长为2cm,
24.【教材呈现】证明:∵P是BD的中点,M是DC的中点,
∴PM=BC,
同理,PN=AD,
∵AD=BC,
∴PM=PN,
∴∠PMN=∠PNM,
【结论应用】(1)证明:∵P是BD的中点,M是DC的中点,
∴PM∥BC,
∴∠PMN=∠F,
同理,∠PNM=∠AEN,
∵∠PMN=∠PNM,
∴∠AEN=∠F;
(2)解:∵PN∥AD,
∴∠PNB=∠A,
∵∠DPN是△PNB的一个外角,
∴∠DPN=∠PNB+∠ABD=∠A+∠ABD,
∵PM∥BC,
∴∠MPD=∠DBC,
∴∠MPN=∠DPN+∠MPD=∠A+∠ABD+∠DBC=∠A+∠ABC=122°,
∵PM=PN,
∴∠PMN=×(180°﹣122°)=29°,
∴∠F=∠PMN=29°,
故答案为:29°.
25.(1)证明:延长BD交AC于H,
在△ADB和△ADH中,
,
∴△ADB≌△ADH,
∴BD=HD,又E为BC的中点.
∴DE∥AC;
(2)解:∵△ADB≌△ADH,
∴AH=AB=4,
∴CH=AC﹣AH=2,
∵BD=HD,又E为BC的中点,
∴DE=CH=1.
26.证明:连接EH,GH,GF,
∵E、F、G、H分别是BD、BC、AC、AD的中点,
∴AB∥EH∥GF,GH∥BC,∴GH∥BF.
∴四边形EHGF为平行四边形.
∵GE,HF分别为其对角线,
∴EG、HF互相平分.
27.证明:取AD的中点Q,连接EQ、FQ,
∵E,F、Q分别为AB,CD、AD的中点,
∴EQ∥BD,EQ=BD,FQ=AC,FQ∥AC,
∴∠QEF=∠OMN,∠QFE=∠ONM,
∵AC=BD,
∴QE=QF,
∴∠QEF=∠QFE,
∴∠OMN=∠ONM,
∴OM=ON,即△OMN是等腰三角形.
28.解:∵P是BD的中点,E是AB的中点,
∴PE是△ABD的中位线,
∴PE=AD,
同理,PF=BC,
∵AD=BC,
∴PE=PF,
∴∠PFE=∠PEF=20°.
29.证明:∵E,G为AB、BC中点,
∴EG=AC,EG∥AC,
∴∠FEG=∠OQP,
同理,FG=BD,FG∥BD,
∴∠EFG=∠OPQ,
∵AC=BD,
∴EG=FG,
∴∠FEG=∠EFG,
∴∠OPQ=∠OQP,
∴OP=OQ.
30.(1)证明:∵AB=AC.
∴∠ABC=∠ACB,
∵DE∥BC,
∴∠ADE=∠ABC,∠AED=∠ACB,
∴∠ADE=∠AED,
∴AD=AE,
∴DB=EC,
∵点F、G、H分别为BE、DE、BC的中点,
∴FG是△EDB的中位线,FH是△BCE的中位线,
∴FG=BD,FH=CE,
∴FG=FH;
(2)解:延长FG交AC于N,
∵FG是△EDB的中位线,FH是△BCE的中位线,
∴FH∥AC,FN∥AB,
∵FG⊥FH,
∴∠A=90°,
∴当∠A=90°时,FG⊥FH.
1.如图,△ABC中,AB>AC,AE平分∠BAC,BD⊥AE于D,CE⊥AE于E,F为BC的中点,给出结论:①FD∥AC;②FE=FD;③AB﹣AC=DE;④∠BAC+∠DFE=180°.其中正确的是( )
A.①② B.①②③ C.①②④ D.①②③④
2.如图,四边形ABCD中,AB=1,CD=4,M、N分别是AD、BC的中点,则线段MN的取值范围是( )
A.3<MN<5 B.3<MN≤5 C.<MN< D.<MN≤
如图,已知△ABC中,AB=AC,AD是∠BAC的平分线,AE是∠BAC的外角平分线,ED∥AB交AC于点G,下列结论:①AD⊥BC;②AE∥BC;③AE=AG;
④AD2+AE2=4AG2.其中正确结论的个数是( )
A.1 B.2 C.3 D.4
4.如图,在△ABC中,∠C=90°,AB=13,AC=5,D、E分别是AC、AB的中点,则DE的长是( )
A.6.5 B.6 C.5.5 D.
5.△ABC中,AB=7,BC=6,AC=5,点D、E、F分别是三边的中点,则△DEF的周长为( )A.4.5 B.9 C.10 D.12
6.已知等腰三角形的两条中位线的长分别为3和5,则此等腰三角形的周长为( )
A.22 B.26 C.22或26 D.13
7.如图,平行四边形ABCD中,对角线AC、BD交于点O,点E是BC的中点.若OE=3cm,则AB的长为( )
A.3cm B.6cm C.9cm D.12cm
8.如图,BD、CE是△ABC的中线,P、Q分别是BD、CE的中点,则PQ:BC等于( )
A.1:4 B.1:5 C.1:6 D.1:7
9.如图,四边形ABCD中,AB=BC,F为CD的中点,BE为∠ABC的角平分线,过点A作AE⊥BE于点E,连接EF,若AD=4,则EF的长为( )
A.1.5 B. C.2 D.
10.如图,BD为△ABC的中线,E为BD的中点,连接AE并延长交BC于点F,若BC的长为7,则BF的长为( )
A. B. C. D.
11.如图,在△ABC中,点D,E分别是AC,BC的中点,点F是DE上一点,连接AF,CF,且AF⊥CF,若AC=6,EF=1,则AB= .
12.如图,四边形ABCD中,∠A=90°,AB=8,AD=6,点M,N分别为线段BC,AB上的动点(含端点,但点M不与点B重合),点E,F分别为DM,MN的中点,则EF长度的最大值为 .
13.一个三角形的周长是12cm,则这个三角形各边中点围成的三角形的周长为 .
14.如图,△ABC中,BD平分∠ABC,CD⊥BD,垂足为D,E为AC中点.若AB=10,BC=6,则DE的长为 .
15.如图,△ABC中,BD平分∠ABC,AD⊥BD于点D,AD的延长线交BC于点E,F是AC中点,连接DF,若AB=10,BC=24,则DF的长为 .
16.如图,在△ABC中,点D、E分别是AB、AC的中点,连接BE,若AE=3,DE=2.5,∠BEC=90°,则△ABC的周长是 .
17.如图,在△ABC中,点D、E分别是边AB、AC的中点,连接DE,∠ABC的平分线BF交DE于点F,若AB=4,BC=6,则EF的长为 .
18.如图,在△ABC中,D,E,F分别是边AB,BC,CA的中点,四边形BEFD周长为14,则AB+BC的长为 .
19.△ABC中,点D是BC中点,∠A=2∠BED,AB=9,AC﹣AE=3,则BE= .
20.如图,M为钝角△ABC中BC边的中点,经过M的直线MN将△ABC分成了周长相等的两部分.已知AB=6,∠A=120°,则MN= .
21.如图,△ABC,点D,E在边BC上,∠ABC的平分线垂直AE,垂足为N,∠ACB的平分线垂直AD,垂足为M,若BC=16,MN=3,则△ABC的周长为 .
22.如图,△ABC中,若D、E、F分别是AB、AC、CD的中点,连接BF,若四边形BDEF的面积为6,则△ABC的面积= .
23.如图,在△ABC中,AB=12cm,AC=8cm,AD、AE分别是其角平分线和中线,过点C作CG⊥AD于点F,交AB于点G,连接EF,求线段EF的长.
24.【教材呈现】
如图是华师版九年级上册数学教材第80页的第3题,请完成这道题的证明.
【结论应用】
(1)如图②,在上边题目的条件下,延长图①中的线段AD交NM的延长线于点E,延长线段BC交NM的延长线于点F.求证:∠AEN=∠F.
(2)若(1)中的∠A+∠ABC=122°,则∠F的大小为 .
25.如图,△ABC中,AD平分∠BAC,AD⊥BD,E为BC的中点.
(1)求证:DE∥AC;
(2)若AB=4,AC=6,求DE的长.
26.已知:△ABC中,D是BC上的一点,E、F、G、H分别是BD、BC、AC、AD的中点,
求证:EG、HF互相平分.
27.一个对角线相等的四边形ABCD,E、F分别为AB,CD的中点,EF分别交对角线BD,AC于M,N,求证:△OMN是等腰三角形.
28.如图,在四边形ABCD中,P是对角线BD的中点,E、F分别是AB、CD的中点,AD=BC,∠PEF=20°,求∠PFE的度数.
29.如图,在四边形ABCD中,对角线AC=BD,E,F为AB、CD的中点,连接EF交BD、AC于P、Q,取BC中点G,连EG、FG,求证:OP=OQ.
30.如图,在△ABC中,AB=AC,点D是边AB的中点,DE∥BC交AC于点E,连接BE,点F、G、H分别为BE、DE、BC的中点.
(1)求证:FG=FH;
(2)当∠A为多少度时,FG⊥FH?并说明理由.
参考答案
1.解:延长CE交AB于G,延长BD交AC延长线于H,
∵AE平分∠GAC,AE⊥GC,
∴AG=AC,GE=CE,
同理可得,AB=AH,BD=HD,
∵BF=CF,BD=HD,
∴DF∥CH,即DF∥AC,故①正确,
∴DF=CH,
∵GE=CE,BF=CF,
∴EF=BG,
∵GB=AB﹣AG=AH﹣AC=CH,即GB=CH,
∴GB=CH,即EF=DF,故②正确,
∴AB﹣AC=AB﹣AG=BG,
过G作GI⊥BH于I,
∵∠GED=∠EDI=∠GID=90°,
∴四边形GIDE是矩形,
∴GI=ED,
∴BG>GI=ED,
∴AB﹣AC>DE,故③错误;
∵EF∥BG,DF∥HC,
∴∠FED=∠BAD,∠FDE=∠HAD,
∴∠FED+∠FDE=∠BAD+∠HAD=∠BAC,
∵∠FED+∠FDE+∠EFD=180°,
∴∠BAC+∠EFD=180°,故④正确;
故选:C.
2.解:连接AC,取AC的中点H,连接MH、NH,
∵M、H分别是AD、AC的中点,
∴MH=CD=2,
同理可得,NH=AB=,
在△MHN中,MH﹣NH<MN<MH+NH,即<MN<,
当点H在MN上时,MN=MH+NH=,
∴<MN≤,
故选:D.
3.解:连接EC,
∵AB=AC,AD是∠BAC的平分线,
∴AD⊥BC,故①正确;
∵AB=AC,
∴∠B=∠ACB,
∵AE平分∠FAC,
∴∠FAC=2∠FAE,
∵∠FAC=∠B+∠ACB,
∴∠FAE=∠B,
∴AE∥BC,故②正确;
∵AE∥BC,DE∥AB,
∴四边形ABDE是平行四边形,
∴AE=BD,
∵AB=AC,AD⊥BC,
∴CD=BD,
∴AE=CD,
∵AE∥BC,∠ADC=90°,
∴四边形ADCE是矩形,
∴AC=DE,AG=CG,DG=EG,
∴DG=AG=CG=EG,
在Rt△AED中,AD2+AE2=DE2=AC2=(2AG)2=4AG2,故④正确;
∵AE=BD=BC,AG=AC,
∴AG=AE错误(已知没有条件AC=BC),故③错误;
即正确的个数是3个,
故选:C.
4.解:在△ABC中,∠C=90°,AB=13,AC=5,
则BC===12,
∵D、E分别是AC、AB的中点,
∴DE=BC=6,
故选:B.
5.解:∵点D、E、F分别是三边的中点,
∴DE、EF、DF为△ABC的中位线,
∴DE=AB=×7=,DF=AC=×5=,EF=BC=×6=3,
∴△DEF的周长=++3=9,
故选:B.
6.解:等腰三角形的两条中位线长分别为3和5,
根据三角形中位线定理可知,等腰三角形的两边长为6和10,
当腰为10时,则三边长为10,10,6时,周长为26;
当腰为6时,则三边长为6,6,10时,周长为22,
故选:C.
7.解:∵四边形ABCD是平行四边形,
∴OA=OC;
又∵点E是BC的中点,
∴BE=CE,
∴AB=2OE=2×3=6(cm)
故选:B.
8.解:连接DE,连接并延长EP交BC于点F,
∵DE是△ABC中位线,
∴DE=BC,AE=BE,AD=CD,
∴∠EDB=∠DBF,
∵P、Q是BD、CE的中点,
∴DP=BP,
∵在△DEP与△BFP中,
,
∴△DEP≌△BFP(ASA),
∴BF=DE=BC,P是EF中点,
∴FC=BC,
PQ是△EFC中位线,
PQ=FC,
∴PQ:BC=1:4.
故选:A.
9.解:连接CE,
∵AE⊥BE,
∴∠BEA=90°,
∵BE为∠ABC的角平分线,
∴∠ABE=∠CBE,
在△ABE和△CBE中,
,
∴△ABE≌△CBE(SAS),
∴AE=CE,∠BEC=∠BEA=90°,
∴∠AEC=∠BEC+∠BEA=180°,
∴A,E,C共线,
∵F为CD的中点,
∴EF是△ACD的中位线,
∴EF=AD=×4=2,
故选:C.
10.解:取FC的中点H,连接DH,
∵CD=DA,
∴DH是△ACF的中位线,
∴DH∥AF,
∵BE=ED,
∴BF=FH,
∴BF=FH=HC=BC=,
故选:A.
11.解:在Rt△AFC中,点D是AC的中点,AC=6,
∴DF=AC=×6=3,
∵EF=1,
∴DE=DF+EF=3+1=4,
∵点D,E分别是AC,BC的中点,
∴DE是△ABC的中位线,
∴AB=2DE=2×4=8,
故答案为:8.
12.解:连接DN,
∵点E,F分别为DM,MN的中点,
∴EF是△MND的中位线,
∴EF=DN,
当点N与点B重合时,DN最大,此时DN==10,
∴EF长度的最大值为5,
故答案为:5.
13.解:根据题意,画出图形如图示,
∵点D、E、F分别是AB、AC、BC的中点,
∴DE、DF、EF都是△ABC的中位线,
∴DE=BC,DF=AC,EF=AB,
∵△ABC的周长是12cm,
∴AB+CB+AC=12cm,
∴DE+DF+FE=24÷2=6(cm).
故答案是:6cm.
14.解:延长CD交AB于F,
在△BDC和△BDF中,
,
∴△BDC≌△BDF(ASA),
∴BF=BC=6,CD=DF,
∴AF=AB﹣BF=4,
∵CD=DF,CE=EA,
∴DE=AF=2,
故答案为:2.
15.解:在△ADB和△EDB中,
,
∴△ADB≌△EDB(ASA),
∴EB=AB=10,AD=DE,
∵BC=24,
∴CE=BC﹣BE=14,
∵AF=FC,AD=DE,
∴DF=CE=7,
故答案为:7.
16.解:∵点D、E分别是AB、AC的中点,DE=2.5,
∴BC=2DE=5,
∵E是AC的中点,BE⊥AC,
∴EC=AE=3,BA=BC=5,
∴AC=AE+EC=6,
∴△ABC的周长=BA+BC+AC=16,
故答案为:16.
17.解:连接AF并延长交BC于H,
∵点D、E分别为边AB、AC的中点,
∴DE∥BC,DE=BC=3,AF=FH,
在△BFA和△BFH中,
,
∴△BFA≌△BFH(AAS),
∴BH=AB=4,
∵AD=DB,AF=FH,
∴DF=BH=2,
∴EF=DE﹣DF=1,
故答案为:1.
18.解:∵D,E,F分别是边AB,BC,CA的中点,
∴DF∥BC,EF∥AB,DF=BC,EF=AB,
∴四边形BEFD为平行四边形,
∵四边形BEFD周长为14,
∴DF+EF=7,
∴AB+BC=14.
故答案为14.
19.解:过点D作DF∥AC,交AB于F,
∵点D是BC中点,
∴DF=AC,DF∥AC,BF=AF=AB=,
∴∠BFD=∠A,
∵∠A=2∠BED,∠BFD=∠BED+∠EDF,
∴∠EDF=∠BED,
∴FE=FD,
∵AC﹣AE=3,
∴AE=AC﹣3=2FE﹣3,
∴FE+2FE﹣3=,
解得,FE=,
∴BE=BF+FE=7,
故答案为:7.
20.解:如图,延长CA到D,使AD=AB,连接BD.
∵∠BAC=120°,
∴∠BAD=180°﹣∠BAC=60°,
∴△ABD是等边三角形,
∴BD=AB=AD=6.
∵M为钝角△ABC中BC边的中点,经过M的直线MN将△ABC分成了周长相等的两部分,
∴BM=CM,BM+AB+AN=CM+CN,
∴AB+AN=CN,
∴AD+AN=CN,即DN=CN,
∵BM=CM,
∴MN是△BCD的中位线,
∴MN=BD=3.
故答案为:3.
21.解:在△BNA和△BNE中,
,
∴△BNA≌△BNE(ASA),
∴BE=BA,AN=NE,
同理,CD=CA,AM=MD,
∵AM=MD,AN=NE,MN=3,
∴DE=2MN=6,
∵BE+CD﹣BC=DE,
∴AB+AC=BC+DE=22,
∴△ABC的周长=AB+AC+BC=22+16=38,
故答案为:38.
22.解:∵点F是CD的中点,
∴S△DEF=S△CEF,
设S△DEF=S△CEF=x,
∵D、E分别是AB、AC的中点,
∴S△ADE=S△CDE=2x,S△BDC=S△ADC=4x,S△BDF=2x,
∴S 四边形BDEF=3x.
∵S 四边形BDEF=6,
∴3x=6,
∴x=2,
∴S△ABC=2S△BDC=8x=16,
故答案为:16.
23.解:在△AGF和△ACF中,
,
∴△AGF≌△ACF(ASA).
∴AG=AC=8cm,
∴GF=CF,则BG=AB﹣AG=12﹣8=4(cm).
又∵BE=CE,
∴EF是△BCG的中位线.
∴EF=BG=2cm.
答:EF的长为2cm,
24.【教材呈现】证明:∵P是BD的中点,M是DC的中点,
∴PM=BC,
同理,PN=AD,
∵AD=BC,
∴PM=PN,
∴∠PMN=∠PNM,
【结论应用】(1)证明:∵P是BD的中点,M是DC的中点,
∴PM∥BC,
∴∠PMN=∠F,
同理,∠PNM=∠AEN,
∵∠PMN=∠PNM,
∴∠AEN=∠F;
(2)解:∵PN∥AD,
∴∠PNB=∠A,
∵∠DPN是△PNB的一个外角,
∴∠DPN=∠PNB+∠ABD=∠A+∠ABD,
∵PM∥BC,
∴∠MPD=∠DBC,
∴∠MPN=∠DPN+∠MPD=∠A+∠ABD+∠DBC=∠A+∠ABC=122°,
∵PM=PN,
∴∠PMN=×(180°﹣122°)=29°,
∴∠F=∠PMN=29°,
故答案为:29°.
25.(1)证明:延长BD交AC于H,
在△ADB和△ADH中,
,
∴△ADB≌△ADH,
∴BD=HD,又E为BC的中点.
∴DE∥AC;
(2)解:∵△ADB≌△ADH,
∴AH=AB=4,
∴CH=AC﹣AH=2,
∵BD=HD,又E为BC的中点,
∴DE=CH=1.
26.证明:连接EH,GH,GF,
∵E、F、G、H分别是BD、BC、AC、AD的中点,
∴AB∥EH∥GF,GH∥BC,∴GH∥BF.
∴四边形EHGF为平行四边形.
∵GE,HF分别为其对角线,
∴EG、HF互相平分.
27.证明:取AD的中点Q,连接EQ、FQ,
∵E,F、Q分别为AB,CD、AD的中点,
∴EQ∥BD,EQ=BD,FQ=AC,FQ∥AC,
∴∠QEF=∠OMN,∠QFE=∠ONM,
∵AC=BD,
∴QE=QF,
∴∠QEF=∠QFE,
∴∠OMN=∠ONM,
∴OM=ON,即△OMN是等腰三角形.
28.解:∵P是BD的中点,E是AB的中点,
∴PE是△ABD的中位线,
∴PE=AD,
同理,PF=BC,
∵AD=BC,
∴PE=PF,
∴∠PFE=∠PEF=20°.
29.证明:∵E,G为AB、BC中点,
∴EG=AC,EG∥AC,
∴∠FEG=∠OQP,
同理,FG=BD,FG∥BD,
∴∠EFG=∠OPQ,
∵AC=BD,
∴EG=FG,
∴∠FEG=∠EFG,
∴∠OPQ=∠OQP,
∴OP=OQ.
30.(1)证明:∵AB=AC.
∴∠ABC=∠ACB,
∵DE∥BC,
∴∠ADE=∠ABC,∠AED=∠ACB,
∴∠ADE=∠AED,
∴AD=AE,
∴DB=EC,
∵点F、G、H分别为BE、DE、BC的中点,
∴FG是△EDB的中位线,FH是△BCE的中位线,
∴FG=BD,FH=CE,
∴FG=FH;
(2)解:延长FG交AC于N,
∵FG是△EDB的中位线,FH是△BCE的中位线,
∴FH∥AC,FN∥AB,
∵FG⊥FH,
∴∠A=90°,
∴当∠A=90°时,FG⊥FH.
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
