第3章数据分析初步 单元综合提升训练-2020-2021学年浙教版八年级数学下册(Word版 含解析)
文档属性
| 名称 | 第3章数据分析初步 单元综合提升训练-2020-2021学年浙教版八年级数学下册(Word版 含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 110.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-08 00:00:00 | ||
图片预览




文档简介
2020-2021年度浙教版八年级数学下册《第3章数据分析初步》单元综合提升训练(附答案)
1.某班篮球爱好小组10名队员进行定点投篮练习,每人投篮10次,将他们投中的次数进行统计,制成如表:
投中次数 2 3 5 6 7 8
人数 1 2 3 2 1 1
则关于这10名队员投中次数组成的数据,下列说法错误的是( )
A.平均数为5 B.中位数为5 C.众数为5 D.方差为5
2.参加第六届京津冀羽毛球冠军挑战赛的一个代表队的年龄分别是49,20,20,25,31,40,46,20,44,25,这组数据的平均数,众数,中位数分别是( )
A.33,21,27 B.32,20,28 C.33,49,27 D.32,21,22
3.有15名学生参加学校举办的“最强大脑”智力竞赛,比赛结束后根据每个学生的成绩计算平均数、中位数、众数、方差,若去掉一个最高分,一个最低分,则一定不会发生变化的是( )
A.平均数 B.中位数 C.众数 D.方差
4.对于一组数据﹣1,﹣1,4,2,下列结论不正确的是( )
A.平均数是1 B.方差是3.5
C.中位数是0.5 D.众数是﹣1
5.数据2021,2021,2021,2021,2021,2021,2021,2021的方差是( )
A.2021 B.0 C.﹣2021 D.2020
6.某校七年级学生的平均年龄为13岁,年龄的方差为3,若学生人数没有变动,则两年后的同一批学生,对其年龄的说法正确的是( )
A.平均年龄为13岁,方差改变 B.平均年龄为15岁,方差不变
C.平均年龄为15岁,方差改变 D.平均年龄为13岁,方差不变
7.某校为了解学生在“慈善募捐”活动中的捐款情况,进行了抽样调查,结果如表所示.
捐款金额(元) 5 10 20 50 100 200
人数 8 10 12 13 5 2
那么该样本中学生捐款金额的中位数和众数分别是( )
A.20元,50元 B.35元,50元 C.50元,50元 D.20元,20元
8.如果一组数据为﹣1,0,1,0,0,那么下列说法不正确的是( )
A.这组数据的方差是0 B.这组数据的众数是0
C.这组数据的中位数是0 D.这组数据的平均数是0
9.已知一组数据5,4,3,4,9,关于这组数据的下列描述,其中错误的描述为( )
A.平均数是5 B.中位数是4 C.众数是4 D.方差是22
10.某公司六位员工的月工资分别是4000元,5000元,5000元,5500元,7000元,10000元,这些数据的( )
A.中位数>众数>平均数 B.中位数>平均数>众数
C.平均数>众数>中位数 D.平均数>中位数>众数
11.一组数据1,1,x,2,4,5的平均数是3,则这组数据的中位数是 .
12.从甲、乙、丙三人中选一人参加环保知识抢答赛,经过两轮初赛,他们的平均成绩都是89,方差分别是S甲2=1.2,S乙2=3.3,S丙2=11.5.你认为适合选 参加决赛.
13.小明在跳绳考核中,前4次跳绳成绩(次数/分钟)记录为:180,178,180,177,若要使5次跳绳成绩的平均数与众数相同,则小明第5次跳绳成绩是 .
14.五个整数中,中位数是2,唯一的众数是4,则这五个数和的最大值是 .
15.若一组数据2、3、x、4、4的平均数是3,则这组数据的方差为 .
16.已知数据x1,x2,…,xn的平均数是3,方差是3,则数据x1+3,x2+3,x3+3,…,xn+3的平均数是 ,方差是 .
17.某中学规定学生的学期体育总评成绩参照学生的平时成绩、期中成绩和期末成绩计算综合得分,其中平时成绩占20%,期中考试成绩占30%,期末考试成绩占50%,小宇的三项成绩(百分制)依次为95分,90分,88分,则小宇这学期的体育总评成绩为 分.
18.已知一组数据:x1,x2,x3,…,xn的平均数是2,则另一组数据:3x1﹣2,3x2﹣2,…3xn﹣2的平均数是 .
19.某公司欲招聘职员,对应聘者进行三项测试:语言、创新、综合知识,并按测试得分1:3:2的比例确定测试总分,已知某位应聘者三项得分(单位:分)分别为86,72,50,则这位应聘者的测试总分为 .
20.小宇在纸上写了六个两两不等的数x1,x2,x3,x4,x5,x6,并记录下这组数的中位数m1和方差S12,然后他将这六个数中大于m1的三个数分别加1,小于m1的三个数分别减1,得到了新的一组数,再次记录下新的这组数的中位数m2和方差S22,则m1 m2,S12 S22(两空均选填“>”,“=”或“<”).
21.某班为了解班级同学寒假期间在家进行体育锻炼的情况,通过钉钉线上运动打卡活动,统计了班级40名同学一段时间的运动打卡次数如表:
打卡次数 6 8 9 10 12 14 15
人数 3 5 4 11 5 4 8
(1)求这40名同学打卡次数的平均数.
(2)为了调动大多数同学锻炼的积极性,班主任准备制定一个打卡奖励标准,凡打卡次数达到或超过这个标准的同学将获得奖励的措施.如果你是班主任,从平均数、中位数、众数的角度进行分析,你将如何确定这个“打卡奖励”标准?
22.小明本学期的数学成绩如表所示:
测验类别 平时成绩1 平时成绩2 平时成绩3 平时成绩4 平时平均数 期中考试 期末考试
成绩 108 103 101 108 a 110 114
(1)六次测试成绩的中位数和众数分别是什么?
(2)请计算出小明该学期的平时成绩平均分a的值;
(3)如果学期的数学总评成绩是根据一定的权重计算所得,其中平时成绩a所占权重为20%,已知小明该学期的总评成绩为111分,请计算出期中考试和期末考试各自所占权重.
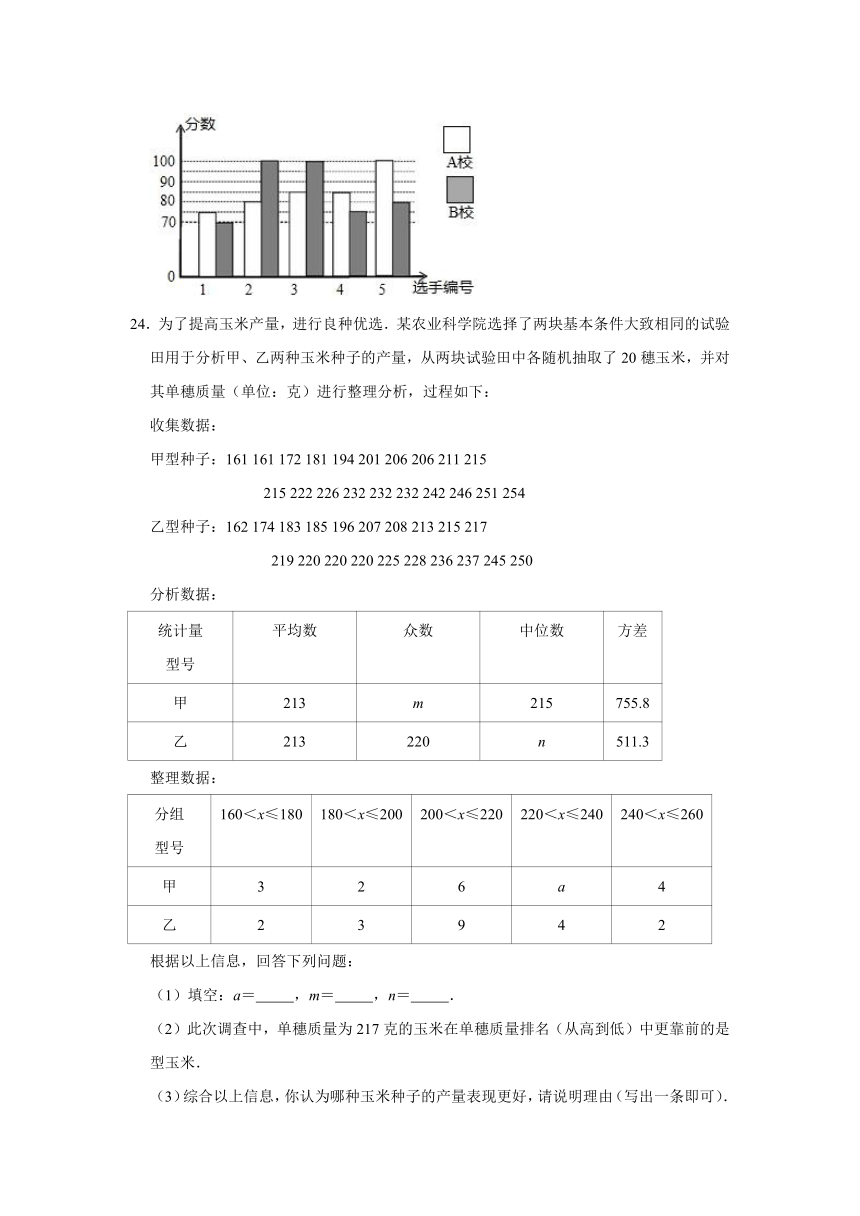
23.某市举行知识大赛,A校、B校各派出5名选手组成代表队参加比赛.两校派出选手的比赛成绩如图所示.
根据以上信息.整理分析数据:
平均数/分 中位数/分 众数/分
A校 85 85 85
B校 85 a b
(1)a= ;b= ;
(2)填空:(填“A校”或“B校”)
①从两校比赛成绩的平均数和中位数的角度来比较,成绩较好的是 ;
②从两校比赛成绩的平均数和众数的角度来比较,成绩较好的是 ;
③从两校比赛成绩的方差的角度来比较, 代表队选手成绩的方差较大.
24.为了提高玉米产量,进行良种优选.某农业科学院选择了两块基本条件大致相同的试验田用于分析甲、乙两种玉米种子的产量,从两块试验田中各随机抽取了20穗玉米,并对其单穗质量(单位:克)进行整理分析,过程如下:
收集数据:
甲型种子:161 161 172 181 194 201 206 206 211 215
215 222 226 232 232 232 242 246 251 254
乙型种子:162 174 183 185 196 207 208 213 215 217
219 220 220 220 225 228 236 237 245 250
分析数据:
统计量 型号 平均数 众数 中位数 方差
甲 213 m 215 755.8
乙 213 220 n 511.3
整理数据:
分组 型号 160<x≤180 180<x≤200 200<x≤220 220<x≤240 240<x≤260
甲 3 2 6 a 4
乙 2 3 9 4 2
根据以上信息,回答下列问题:
(1)填空:a= ,m= ,n= .
(2)此次调查中,单穗质量为217克的玉米在单穗质量排名(从高到低)中更靠前的是 型玉米.
(3)综合以上信息,你认为哪种玉米种子的产量表现更好,请说明理由(写出一条即可).
25.某球队对甲、乙两名运动员进行3分球投篮测试,测试共五组,每组投10次,进球的个数统计结果如下:
甲:9,9,9,6,7;
乙:4,9,8,9,10;
列表进行数据分析:
选手 平均成绩 中位数 众数 方差
甲 8 b 9 d
乙 a 9 c 4.4
(1)b= ,c= ;
(2)试计算乙的平均成绩a和甲的方差d;(计算方差的公式:s2=[(x1﹣)2+(x2﹣)2+…+(xn﹣)2])
(3)根据以上数据分析,如果你是教练,你会选择哪名队员参加3分球大赛?请说明理由.
26.某中学举办“信息技术知识答题竞赛”,八、九年级根据初赛成绩各选出5名选手组成代表队参加学校决赛,现将两个队各选出的5名选手的决赛成绩绘制成如下统计图表.
平均分
(分) 中位数
(分) 众数
(分) 方差
(分2)
八年级 85 a 85 70
九年级 b 80 c s2
(1)根据图表信息填空:a= ,b= ,c= ;
(2)计算九年级代表队决赛成绩的方差,并判断哪一个代表队选手成绩较为稳定.
参考答案
1.解:这组数据的平均数为=5,故A选项正确,不符合题意;
中位数为=5,故B选项正确,不符合题意;
众数为5,故C选项正确,不符合题意;
方差为×[(2﹣5)2+2×(3﹣5)2+3×(5﹣5)2+2×(6﹣5)2+(7﹣5)2+(8﹣5)2]=2.8,故D选项错误,符合题意;
故选:D.
2.解:这组数据的平均数是:(49+20+20+25+31+40+46+20+44+25)÷10=32(岁),
这组数据出现最多的数是20,所以这组数据的众数是20岁;
把这些数按从小到大的顺序排列为:20,20,20,25,25,31,40,44,46,49,
则这组数据的中位数是:(25+31)÷2=28(岁).
故选:B.
3.解:去掉一个最高分和一个最低分对中位数没有影响.
故选:B.
4.解:将这组数据重新排列为﹣1、﹣1、2、4,
所以这组数据的平均数为=1,中位数为=0.5,众数为﹣1,
方差为×[2×(﹣1﹣1)2+(2﹣1)2+(4﹣1)2]=4.25,
故选:B.
5.解:∵这组数据全部相等,均为2021,
∴这组数据没有波动,
∴这组数据的方差为0,
故选:B.
6.解:两年后的同一批学生的年龄均增加2岁,其年龄的波动幅度不变,
所以平均年龄为15岁,方差不变,
故选:B.
7.解:该样本中学生捐款金额的中位数为=20(元),众数为50元,
故选:A.
8.解:这组数据重新排列为﹣1、0、0、0、1,
其众数是0,中位数为0,平均数为=0,
方差为×[(﹣1﹣0)2+3×(0﹣0)2+(1﹣0)2]=,
故选:A.
9.解:将这组数据重新排列为3、4、4、5、9,
所以这组数据的平均数为=5,中位数为4,众数为4,
方差为×[(3﹣4)2+2×(4﹣4)2+(5﹣4)2+(9﹣4)2]=5.4,
故选:D.
10.解:这组数据的中位数为=5250(元),众数为5000元,平均数为=6083(元),
∴平均数>中位数>众数,
故选:D.
11.解:∵数据1,1,x,2,4,5的平均数是3,
∴=3,
解得x=5,
所以这组数据为1,1,2,4,5,5,
则这组数据的中位数为=3,
故答案为:3.
12.解:∵S甲2=1.2,S乙2=3.3,S丙2=11.5,
∴S甲2<S乙2<S丙2,
∴甲的成绩稳定,
∴适合选择甲参加决赛,
故答案为:甲.
13.解:设小明第5次跳绳成绩是x次数/分钟,
根据题意得,(180+178+180+177+x)=180,
解得,x=185.
故答案为:185.
14.解:因为五个整数从小到大排列后,其中位数是2,这组数据的唯一众数是4.
所以这5个数据分别是x,y,2,4,4,且x<y<2,
当这5个数的和最大时,整数x,y取最大值,此时x=0,y=1,
所以这组数据可能的最大的和是0+1+2+4+4=11.
故答案为:11.
15.解:∵2、3、x、4、4的平均数是3,
∴2+3+x+4+4=3×5,解得x=2,
数据为:2、2、3、4、4,
∴S2=[(2﹣3)2+(2﹣3)2+(3﹣3)2+(4﹣3)2+(4﹣3)2]=0.8.
故答案为0.8.
16.解:∵数据x1,x2,…,xn的平均数是3,方差是3,
∴数据x1+3,x2+3,x3+3,…,xn+3的平均数是3+3=6,方差是3,
故答案为:6,3.
17.解:小宇这学期的体育总评成绩为95×20%+90×30%+88×50%=90(分),
故答案为:90分.
18.解:∵数据x1,x2,x3,…,xn的平均数是2,
∴数据3x1,3x2,…3xn的平均数是3×2=6,
∴数据3x1﹣2,3x2﹣2,…3xn﹣2的平均数是6﹣2=4.
故答案为:4.
19.解:=67(分),
即这位应聘者的测试总分为67分,
故答案为:67分.
20.解:把数x1,x2,x3,x4,x5,x6从小到大排列,将这六个数中大于m1的三个数分别加1,小于m1的三个数分别减1,则第3个数和第4个数的位置不改变,这两个数的平均数没有变,所以m1=m2,
又因为新数据的平均数与原数据的平均数相等,所以新数据的波动性大,即S12<S22.
故答案为=,<.
21.解:(1)平均数为(6×3+8×5+9×4+10×11+12×5+14×4+15×8)÷40=11.
即这40名同学打卡次数的平均数为11次;
(2)共40人,所有同学打卡次数从小到大排列第20个、第21个数都为10次,
所以中位数为10次;
10出现了11次,次数最多,众数为10次;
为了调动同学们锻炼的积极性,“打卡奖励”标准可以定为所有同学打卡次数的中位数或众数.
因为共有40人,10次以上(含10次)的有28人,超过总数的一半.
22.解:(1)六次数据依次为:101、103、108、108、110、114,
则中位数为:108,众数为:108;
(2)a==105;
(3)设期中考试所占权重是x,期末考试所占权重是y,
由题意得,
解得:.
答:期中考试所占权重是30%,期末考试所占权重是50%.
23.解:(1)将B校5名选手的成绩重新排列为:70、75、80、100、100,
所以其中位数a=80、众数b=100,
故答案为:80、100;
(2)①从两校比赛成绩的平均数和中位数的角度来比较,成绩较好的是A校;
②从两校比赛成绩的平均数和众数的角度来比较,成绩较好的是B校;
③=×[(75﹣85)2+(80﹣85)2+2×(85﹣85)2+(100﹣85)2]=70,
=×[(70﹣85)2+(75﹣85)2+(80﹣85)2+2×(100﹣85)2]=160,
∴从两校比赛成绩的方差的角度来比较,B校代表队选手成绩的方差较大.
故答案为:A校、B校、B校.
24.解:(1)将甲型种子抽样20穗质量进行分组统计,可得220<x≤240的频数为5,即a=5,
甲型种子抽样20穗质量出现次数最多的是232,共出现3次,因此众数为232,即m=232,
将乙型种子抽样20穗质量从小到大排列后,处在中间位置的两个数的平均数为=218,即中位数是218,也就是n=218,
故答案为:5,232,218;
(2)甲;
(3)乙型玉米种子的产量表现更好,理由:乙型种子单穗质量的中位数大于甲型种子单穗质量的中位数,什么乙型种子大部分质量关于甲型(答案不唯一).
25.解:∵将甲的5个数据按照由小到大的顺序排列:6,7,9,9,9,
位置在最中间的是9,
∴这组数据的中位数为9.
∴b=9.
∵乙的5个数据中9出现了两次,出现次数最多,
∴乙组数据的众数为:9.
∴c=9.
故答案为:9;9.
(2)乙的平均数a==8.
∵方差的公式:s2=[(x1﹣)2+(x2﹣)2+…+(xn﹣)2],
∴d=[(9﹣8)2+(9﹣8)2+(9﹣8)2+(6﹣8)2+(7﹣8)2]=1.6.
(3)选择甲选手参加比赛.
理由:∵甲,乙的平均成绩都为8,中位数都为9,众数都为9,
但甲的方差d=1.6<乙的方差4.4
∴在平均数、中位数、众数都相同的情况下,甲的方差比乙小,
故甲比乙稳定,选择甲.
26.解:(1)由题意,a=85,b==85,c=100.
故答案为:85,85,100.
(2).
∵160<70,
∴八年级代表队选手成绩较为稳定.
1.某班篮球爱好小组10名队员进行定点投篮练习,每人投篮10次,将他们投中的次数进行统计,制成如表:
投中次数 2 3 5 6 7 8
人数 1 2 3 2 1 1
则关于这10名队员投中次数组成的数据,下列说法错误的是( )
A.平均数为5 B.中位数为5 C.众数为5 D.方差为5
2.参加第六届京津冀羽毛球冠军挑战赛的一个代表队的年龄分别是49,20,20,25,31,40,46,20,44,25,这组数据的平均数,众数,中位数分别是( )
A.33,21,27 B.32,20,28 C.33,49,27 D.32,21,22
3.有15名学生参加学校举办的“最强大脑”智力竞赛,比赛结束后根据每个学生的成绩计算平均数、中位数、众数、方差,若去掉一个最高分,一个最低分,则一定不会发生变化的是( )
A.平均数 B.中位数 C.众数 D.方差
4.对于一组数据﹣1,﹣1,4,2,下列结论不正确的是( )
A.平均数是1 B.方差是3.5
C.中位数是0.5 D.众数是﹣1
5.数据2021,2021,2021,2021,2021,2021,2021,2021的方差是( )
A.2021 B.0 C.﹣2021 D.2020
6.某校七年级学生的平均年龄为13岁,年龄的方差为3,若学生人数没有变动,则两年后的同一批学生,对其年龄的说法正确的是( )
A.平均年龄为13岁,方差改变 B.平均年龄为15岁,方差不变
C.平均年龄为15岁,方差改变 D.平均年龄为13岁,方差不变
7.某校为了解学生在“慈善募捐”活动中的捐款情况,进行了抽样调查,结果如表所示.
捐款金额(元) 5 10 20 50 100 200
人数 8 10 12 13 5 2
那么该样本中学生捐款金额的中位数和众数分别是( )
A.20元,50元 B.35元,50元 C.50元,50元 D.20元,20元
8.如果一组数据为﹣1,0,1,0,0,那么下列说法不正确的是( )
A.这组数据的方差是0 B.这组数据的众数是0
C.这组数据的中位数是0 D.这组数据的平均数是0
9.已知一组数据5,4,3,4,9,关于这组数据的下列描述,其中错误的描述为( )
A.平均数是5 B.中位数是4 C.众数是4 D.方差是22
10.某公司六位员工的月工资分别是4000元,5000元,5000元,5500元,7000元,10000元,这些数据的( )
A.中位数>众数>平均数 B.中位数>平均数>众数
C.平均数>众数>中位数 D.平均数>中位数>众数
11.一组数据1,1,x,2,4,5的平均数是3,则这组数据的中位数是 .
12.从甲、乙、丙三人中选一人参加环保知识抢答赛,经过两轮初赛,他们的平均成绩都是89,方差分别是S甲2=1.2,S乙2=3.3,S丙2=11.5.你认为适合选 参加决赛.
13.小明在跳绳考核中,前4次跳绳成绩(次数/分钟)记录为:180,178,180,177,若要使5次跳绳成绩的平均数与众数相同,则小明第5次跳绳成绩是 .
14.五个整数中,中位数是2,唯一的众数是4,则这五个数和的最大值是 .
15.若一组数据2、3、x、4、4的平均数是3,则这组数据的方差为 .
16.已知数据x1,x2,…,xn的平均数是3,方差是3,则数据x1+3,x2+3,x3+3,…,xn+3的平均数是 ,方差是 .
17.某中学规定学生的学期体育总评成绩参照学生的平时成绩、期中成绩和期末成绩计算综合得分,其中平时成绩占20%,期中考试成绩占30%,期末考试成绩占50%,小宇的三项成绩(百分制)依次为95分,90分,88分,则小宇这学期的体育总评成绩为 分.
18.已知一组数据:x1,x2,x3,…,xn的平均数是2,则另一组数据:3x1﹣2,3x2﹣2,…3xn﹣2的平均数是 .
19.某公司欲招聘职员,对应聘者进行三项测试:语言、创新、综合知识,并按测试得分1:3:2的比例确定测试总分,已知某位应聘者三项得分(单位:分)分别为86,72,50,则这位应聘者的测试总分为 .
20.小宇在纸上写了六个两两不等的数x1,x2,x3,x4,x5,x6,并记录下这组数的中位数m1和方差S12,然后他将这六个数中大于m1的三个数分别加1,小于m1的三个数分别减1,得到了新的一组数,再次记录下新的这组数的中位数m2和方差S22,则m1 m2,S12 S22(两空均选填“>”,“=”或“<”).
21.某班为了解班级同学寒假期间在家进行体育锻炼的情况,通过钉钉线上运动打卡活动,统计了班级40名同学一段时间的运动打卡次数如表:
打卡次数 6 8 9 10 12 14 15
人数 3 5 4 11 5 4 8
(1)求这40名同学打卡次数的平均数.
(2)为了调动大多数同学锻炼的积极性,班主任准备制定一个打卡奖励标准,凡打卡次数达到或超过这个标准的同学将获得奖励的措施.如果你是班主任,从平均数、中位数、众数的角度进行分析,你将如何确定这个“打卡奖励”标准?
22.小明本学期的数学成绩如表所示:
测验类别 平时成绩1 平时成绩2 平时成绩3 平时成绩4 平时平均数 期中考试 期末考试
成绩 108 103 101 108 a 110 114
(1)六次测试成绩的中位数和众数分别是什么?
(2)请计算出小明该学期的平时成绩平均分a的值;
(3)如果学期的数学总评成绩是根据一定的权重计算所得,其中平时成绩a所占权重为20%,已知小明该学期的总评成绩为111分,请计算出期中考试和期末考试各自所占权重.
23.某市举行知识大赛,A校、B校各派出5名选手组成代表队参加比赛.两校派出选手的比赛成绩如图所示.
根据以上信息.整理分析数据:
平均数/分 中位数/分 众数/分
A校 85 85 85
B校 85 a b
(1)a= ;b= ;
(2)填空:(填“A校”或“B校”)
①从两校比赛成绩的平均数和中位数的角度来比较,成绩较好的是 ;
②从两校比赛成绩的平均数和众数的角度来比较,成绩较好的是 ;
③从两校比赛成绩的方差的角度来比较, 代表队选手成绩的方差较大.
24.为了提高玉米产量,进行良种优选.某农业科学院选择了两块基本条件大致相同的试验田用于分析甲、乙两种玉米种子的产量,从两块试验田中各随机抽取了20穗玉米,并对其单穗质量(单位:克)进行整理分析,过程如下:
收集数据:
甲型种子:161 161 172 181 194 201 206 206 211 215
215 222 226 232 232 232 242 246 251 254
乙型种子:162 174 183 185 196 207 208 213 215 217
219 220 220 220 225 228 236 237 245 250
分析数据:
统计量 型号 平均数 众数 中位数 方差
甲 213 m 215 755.8
乙 213 220 n 511.3
整理数据:
分组 型号 160<x≤180 180<x≤200 200<x≤220 220<x≤240 240<x≤260
甲 3 2 6 a 4
乙 2 3 9 4 2
根据以上信息,回答下列问题:
(1)填空:a= ,m= ,n= .
(2)此次调查中,单穗质量为217克的玉米在单穗质量排名(从高到低)中更靠前的是 型玉米.
(3)综合以上信息,你认为哪种玉米种子的产量表现更好,请说明理由(写出一条即可).
25.某球队对甲、乙两名运动员进行3分球投篮测试,测试共五组,每组投10次,进球的个数统计结果如下:
甲:9,9,9,6,7;
乙:4,9,8,9,10;
列表进行数据分析:
选手 平均成绩 中位数 众数 方差
甲 8 b 9 d
乙 a 9 c 4.4
(1)b= ,c= ;
(2)试计算乙的平均成绩a和甲的方差d;(计算方差的公式:s2=[(x1﹣)2+(x2﹣)2+…+(xn﹣)2])
(3)根据以上数据分析,如果你是教练,你会选择哪名队员参加3分球大赛?请说明理由.
26.某中学举办“信息技术知识答题竞赛”,八、九年级根据初赛成绩各选出5名选手组成代表队参加学校决赛,现将两个队各选出的5名选手的决赛成绩绘制成如下统计图表.
平均分
(分) 中位数
(分) 众数
(分) 方差
(分2)
八年级 85 a 85 70
九年级 b 80 c s2
(1)根据图表信息填空:a= ,b= ,c= ;
(2)计算九年级代表队决赛成绩的方差,并判断哪一个代表队选手成绩较为稳定.
参考答案
1.解:这组数据的平均数为=5,故A选项正确,不符合题意;
中位数为=5,故B选项正确,不符合题意;
众数为5,故C选项正确,不符合题意;
方差为×[(2﹣5)2+2×(3﹣5)2+3×(5﹣5)2+2×(6﹣5)2+(7﹣5)2+(8﹣5)2]=2.8,故D选项错误,符合题意;
故选:D.
2.解:这组数据的平均数是:(49+20+20+25+31+40+46+20+44+25)÷10=32(岁),
这组数据出现最多的数是20,所以这组数据的众数是20岁;
把这些数按从小到大的顺序排列为:20,20,20,25,25,31,40,44,46,49,
则这组数据的中位数是:(25+31)÷2=28(岁).
故选:B.
3.解:去掉一个最高分和一个最低分对中位数没有影响.
故选:B.
4.解:将这组数据重新排列为﹣1、﹣1、2、4,
所以这组数据的平均数为=1,中位数为=0.5,众数为﹣1,
方差为×[2×(﹣1﹣1)2+(2﹣1)2+(4﹣1)2]=4.25,
故选:B.
5.解:∵这组数据全部相等,均为2021,
∴这组数据没有波动,
∴这组数据的方差为0,
故选:B.
6.解:两年后的同一批学生的年龄均增加2岁,其年龄的波动幅度不变,
所以平均年龄为15岁,方差不变,
故选:B.
7.解:该样本中学生捐款金额的中位数为=20(元),众数为50元,
故选:A.
8.解:这组数据重新排列为﹣1、0、0、0、1,
其众数是0,中位数为0,平均数为=0,
方差为×[(﹣1﹣0)2+3×(0﹣0)2+(1﹣0)2]=,
故选:A.
9.解:将这组数据重新排列为3、4、4、5、9,
所以这组数据的平均数为=5,中位数为4,众数为4,
方差为×[(3﹣4)2+2×(4﹣4)2+(5﹣4)2+(9﹣4)2]=5.4,
故选:D.
10.解:这组数据的中位数为=5250(元),众数为5000元,平均数为=6083(元),
∴平均数>中位数>众数,
故选:D.
11.解:∵数据1,1,x,2,4,5的平均数是3,
∴=3,
解得x=5,
所以这组数据为1,1,2,4,5,5,
则这组数据的中位数为=3,
故答案为:3.
12.解:∵S甲2=1.2,S乙2=3.3,S丙2=11.5,
∴S甲2<S乙2<S丙2,
∴甲的成绩稳定,
∴适合选择甲参加决赛,
故答案为:甲.
13.解:设小明第5次跳绳成绩是x次数/分钟,
根据题意得,(180+178+180+177+x)=180,
解得,x=185.
故答案为:185.
14.解:因为五个整数从小到大排列后,其中位数是2,这组数据的唯一众数是4.
所以这5个数据分别是x,y,2,4,4,且x<y<2,
当这5个数的和最大时,整数x,y取最大值,此时x=0,y=1,
所以这组数据可能的最大的和是0+1+2+4+4=11.
故答案为:11.
15.解:∵2、3、x、4、4的平均数是3,
∴2+3+x+4+4=3×5,解得x=2,
数据为:2、2、3、4、4,
∴S2=[(2﹣3)2+(2﹣3)2+(3﹣3)2+(4﹣3)2+(4﹣3)2]=0.8.
故答案为0.8.
16.解:∵数据x1,x2,…,xn的平均数是3,方差是3,
∴数据x1+3,x2+3,x3+3,…,xn+3的平均数是3+3=6,方差是3,
故答案为:6,3.
17.解:小宇这学期的体育总评成绩为95×20%+90×30%+88×50%=90(分),
故答案为:90分.
18.解:∵数据x1,x2,x3,…,xn的平均数是2,
∴数据3x1,3x2,…3xn的平均数是3×2=6,
∴数据3x1﹣2,3x2﹣2,…3xn﹣2的平均数是6﹣2=4.
故答案为:4.
19.解:=67(分),
即这位应聘者的测试总分为67分,
故答案为:67分.
20.解:把数x1,x2,x3,x4,x5,x6从小到大排列,将这六个数中大于m1的三个数分别加1,小于m1的三个数分别减1,则第3个数和第4个数的位置不改变,这两个数的平均数没有变,所以m1=m2,
又因为新数据的平均数与原数据的平均数相等,所以新数据的波动性大,即S12<S22.
故答案为=,<.
21.解:(1)平均数为(6×3+8×5+9×4+10×11+12×5+14×4+15×8)÷40=11.
即这40名同学打卡次数的平均数为11次;
(2)共40人,所有同学打卡次数从小到大排列第20个、第21个数都为10次,
所以中位数为10次;
10出现了11次,次数最多,众数为10次;
为了调动同学们锻炼的积极性,“打卡奖励”标准可以定为所有同学打卡次数的中位数或众数.
因为共有40人,10次以上(含10次)的有28人,超过总数的一半.
22.解:(1)六次数据依次为:101、103、108、108、110、114,
则中位数为:108,众数为:108;
(2)a==105;
(3)设期中考试所占权重是x,期末考试所占权重是y,
由题意得,
解得:.
答:期中考试所占权重是30%,期末考试所占权重是50%.
23.解:(1)将B校5名选手的成绩重新排列为:70、75、80、100、100,
所以其中位数a=80、众数b=100,
故答案为:80、100;
(2)①从两校比赛成绩的平均数和中位数的角度来比较,成绩较好的是A校;
②从两校比赛成绩的平均数和众数的角度来比较,成绩较好的是B校;
③=×[(75﹣85)2+(80﹣85)2+2×(85﹣85)2+(100﹣85)2]=70,
=×[(70﹣85)2+(75﹣85)2+(80﹣85)2+2×(100﹣85)2]=160,
∴从两校比赛成绩的方差的角度来比较,B校代表队选手成绩的方差较大.
故答案为:A校、B校、B校.
24.解:(1)将甲型种子抽样20穗质量进行分组统计,可得220<x≤240的频数为5,即a=5,
甲型种子抽样20穗质量出现次数最多的是232,共出现3次,因此众数为232,即m=232,
将乙型种子抽样20穗质量从小到大排列后,处在中间位置的两个数的平均数为=218,即中位数是218,也就是n=218,
故答案为:5,232,218;
(2)甲;
(3)乙型玉米种子的产量表现更好,理由:乙型种子单穗质量的中位数大于甲型种子单穗质量的中位数,什么乙型种子大部分质量关于甲型(答案不唯一).
25.解:∵将甲的5个数据按照由小到大的顺序排列:6,7,9,9,9,
位置在最中间的是9,
∴这组数据的中位数为9.
∴b=9.
∵乙的5个数据中9出现了两次,出现次数最多,
∴乙组数据的众数为:9.
∴c=9.
故答案为:9;9.
(2)乙的平均数a==8.
∵方差的公式:s2=[(x1﹣)2+(x2﹣)2+…+(xn﹣)2],
∴d=[(9﹣8)2+(9﹣8)2+(9﹣8)2+(6﹣8)2+(7﹣8)2]=1.6.
(3)选择甲选手参加比赛.
理由:∵甲,乙的平均成绩都为8,中位数都为9,众数都为9,
但甲的方差d=1.6<乙的方差4.4
∴在平均数、中位数、众数都相同的情况下,甲的方差比乙小,
故甲比乙稳定,选择甲.
26.解:(1)由题意,a=85,b==85,c=100.
故答案为:85,85,100.
(2).
∵160<70,
∴八年级代表队选手成绩较为稳定.
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
