5.2.2菱形的判定 同步练习(含解析)
文档属性
| 名称 | 5.2.2菱形的判定 同步练习(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-11 00:00:00 | ||
图片预览



文档简介
初中数学浙教版八年级下册5.2.2菱形的判定 同步练习
一、单选题
1.如图,四边形ABCD沿直线l对折后重合,如果 AD//BC ,则结论①AB // CD;②AB=CD;③ AB⊥BC ;④ AO=OC 中正确的是(? )
A.?1个???????????????????????????????????????B.?2个???????????????????????????????????????C.?3个???????????????????????????????????????D.?4个
2.如图,在 △ABC 中,点D在边BC上,过点D作 DE//AC , DF//AB ,分别交AB,AC于E,F两点.则下列命题是假命题的是(??? )
A.?四边形 AEDF 是平行四边形?????????????????????????B.?若 ∠B+∠C=90° ,则四边形 AEDF 是矩形
C.?若 BD=CD ,则四边形 AEDF 是菱形???????D.?若 AD=BD ,则四边形 AEDF 是矩形
3.如图,在平行四边形ABCD中,点F是AB的中点,连接DF并延长,交CB的延长线于点E , 连接AE . 添加一个条件,使四边形AEBD是菱形,这个条件是(?? )
A.?∠BAD=∠BDA?????????????????B.?AB=DE?????????????????C.?DF=EF?????????????????D.?DE平分 ∠ADB
4.两张全等的矩形纸片 ABCD,AECF 按如图方式交叉叠放在一起,AB=AF,AE=BC.若 AB=1,BC=3,则图中重叠(阴影)部分的面积为(?? ).
A.?2?????????????????????????????????????????B.?3?????????????????????????????????????????C.?53?????????????????????????????????????????D.?43
5.某班同学在“为抗疫英雄祈福”的主题班会课上制作象征“平安归来”的黄丝带,如图所示,丝带重叠部分形成的图形是(?? )
A.?矩形?????????????????????????????????B.?菱形?????????????????????????????????C.?正方形?????????????????????????????????D.?等腰梯形
6.如图,矩形ABCD的对角线AC、BD相交于点O,CE∥BD,DE∥AC,若AB=4,BC=3,则四边形CODE的周长是( )
A.?5??????????????????????????????????????????B.?8??????????????????????????????????????????C.?10??????????????????????????????????????????D.?12
7.如图,在?ABCD中,用直尺和圆规作∠BAD的平分线AG交BC于点E.若BF=12,AB=10,则AE的长为(??? )
A.?16?????????????????????????????????????????B.?15?????????????????????????????????????????C.?14?????????????????????????????????????????D.?13
8.如图,在 ? ABCD中,DE,BF分别是∠ADC和∠ABC的平分线,添加一个条件,仍无法判断四边形BFDE为菱形的是(??? )
A.?∠A=60????????????????????????B.?DE=DF???????????????????????C.?EF⊥BD???????????????????????D.?BD 是∠EDF的平分线
9.如图,某同学作线段AB的垂直平分线:分别以点A和点B为圆心,大于 12 AB的长为半径画弧,两弧相交于点C,D,则直线CD为线段AB的垂直平分线.根据这个同学的作图方法可知四边形ADBC一定是(?? )
A.?菱形?????????????????????????????B.?平行四边形?????????????????????????????C.?矩形?????????????????????????????D.?一般的四边形
10.已知四边形ABCD是平行四边形,下列结论错误的是(??? )
A.?当AB=BC时,它是菱形??????????????????????????????????????B.?当AC⊥BD时,它是菱形
C.?当 ∠ABC=90? 时,它是矩形??????????????????????????D.?当 AC=BD 时,它是菱形
二、填空题
11.如图,在□ABCD中,以点A为圆心,以任意长为半径画圆弧,分别交边AD、AB于点M、N , 再分别以点M、N为圆心,以大于 12MN 长为半径画圆弧,两弧交于点P , 作射线AP交边CD于点E , 过点E作EF∥AD交AB于点F . 若AB=5,CE=2,则四边形ADEF的周长为________.
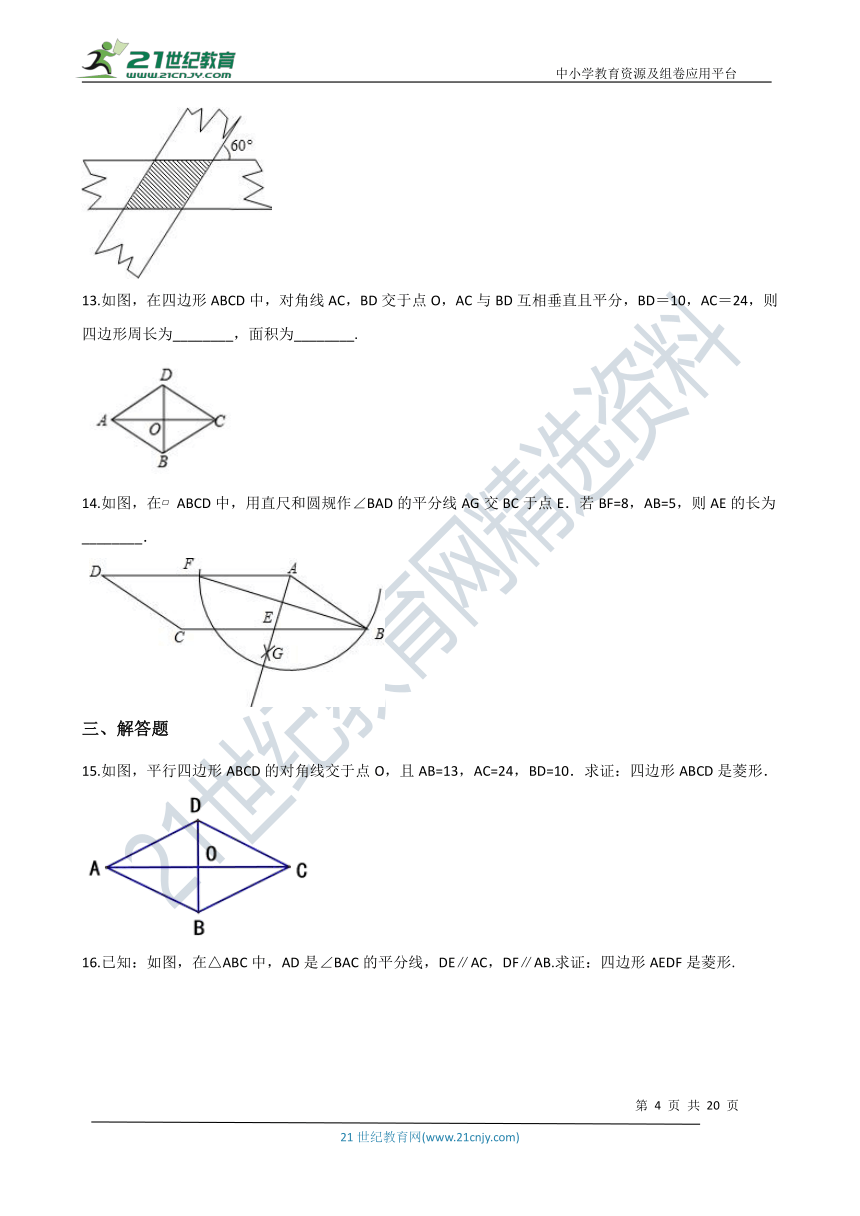
12.如图,小华剪了两条宽为3的纸条,交叉叠放在一起,且它们较小的交角为60°,则它们重叠部分的面积为________.
13.如图,在四边形ABCD中,对角线AC,BD交于点O,AC与BD互相垂直且平分,BD=10,AC=24,则四边形周长为________,面积为________.
14.如图,在?ABCD中,用直尺和圆规作∠BAD的平分线AG交BC于点E.若BF=8,AB=5,则AE的长为________.
三、解答题
15.如图,平行四边形ABCD的对角线交于点O,且AB=13,AC=24,BD=10.求证:四边形ABCD是菱形.
16.已知:如图,在△ABC中,AD是∠BAC的平分线,DE∥AC,DF∥AB.求证:四边形AEDF是菱形.
17.老师布置了一个作业,如下:
已知:如图1 ?ABCD 的对角线 AC 的垂直平分线 EF 交 AD 于点 F ,交 BC 于点 E ,交 AC 于点 O .求证:四边形 AECF 是菱形.
嘉琪同学写出了如图2所示的证明过程,老师说嘉琪同学的作业是错误的.请你解答下列问题:
(1)能找出该同学错误的原因吗?请你指出来;
(2)请你给出本题的符合题意证明过程.
18.如图,在矩形ABCD中,M、N分别是AD、BC的中点,P、Q分别是BM、DN的中点.
(1)求证:△MBA≌△NDC;
(2)四边形MPNQ是什么样的特殊四边形?不用证明.
19.如图,直线y=﹣2x+8分别交x轴,y轴于点A , B , 直线y =12 x+3交y轴于点C , 两直线相交于点D .
(1)求点D的坐标;
(2)如图2,过点A作AE∥y轴交直线y =12 x+3于点E , 连接AC , BE . 求证:四边形ACBE是菱形;
(3)如图3,在(2)的条件下,点F在线段BC上,点G在线段AB上,连接CG , FG , 当CG=FG , 且∠CGF=∠ABC时,求点G的坐标.
答案解析部分
一、单选题
1. C
考点:菱形的判定与性质,轴对称的性质
解:如图所示:
∵直线l是四边形ABCD的对称轴,
∴AB=AD,BC=DC,∠1=∠2,∠3=∠4,
又∵AD∥BC,
∴∠2=∠3,
∴∠1=∠4,
∴AB∥CD,故①正确;
∴四边形ABCD是菱形;
∴AB=CD,故②正确;
∵四边形ABCD是菱形;
∴AO=OC,故④正确.
∵当四边形ABCD是菱形时,直线l是四边形ABCD的对称轴,但是AB与BC不一定垂直,故③错误.
故答案为:C.
分析:根据轴对称图形的性质得出AB=AD,BC=DC,∠1=∠2,∠3=∠4,根据平行线的性质得出∠2=∠3,根据等量代换得出∠1=∠4,进而根据内错角相等,二直线平行得出AB∥CD,根据一组邻边相等且两组对边分别平行的四边形是菱形得出四边形ABCD是菱形,进而根据菱形的性质即可一一判断得出答案.
2. C
考点:平行四边形的判定,菱形的判定,矩形的判定
解: ∵ DE//AC,DF//AB
∴ 四边形AEDF是平行四边形,故A选项不符合题意;
∵ 四边形AEDF是平行四边形, ∠B+∠C=90°
∴∠BAC=90°
∴ 四边形AEDF是矩形,故B选项不符合题意;
∵DE//AC
∴DEAC=BDBC=12
∴DE=12AC
同理 DF=12AB
要想四边形AEDF是菱形,只需 DE=DF ,则需 AC=AB 显然没有这个条件,故C选项符合题意;
∵AD=BD ,则 ∠B=∠DAB , ∠DAC=∠C ,
∵∠B+∠C+∠BAC=180°
∴∠BAC=90°
∴ ∴ 四边形AEDF是矩形,故D选项不符合题意;
故答案为:C.
分析:根据平行四边形、矩形、菱形的判定逐项判定即可。
3. D
考点:菱形的判定
解:在平行四边形ABCD中,AD∥BC,
∴∠DAB=∠EBA,
∵点F是AB的中点,
∴AF=BF,
∵∠AFD=∠BFE,
∴△ADF≌△BEF,
∴AD=BE,
∵AD∥BE,
∴四边形AEBD是平行四边形,
A、当 ∠BAD=∠BDA 时,得到AB=BD,无法判定四边形AEBD是菱形,故该选项不符合题意;
B、AB=BE时,无法判定四边形AEBD是菱形,故该选项不符合题意;
C、DF=EF时,无法判定四边形AEBD是菱形,故该选项不符合题意;
D、当DE平分 ∠ADB 时,四边形AEBD是菱形,故该选项符合题意;
故答案为:D.
分析:先证明△ADF≌△BEF,得到AD=BE,推出四边形AEBD是平行四边形,再逐项分析即可。
4. C
考点:勾股定理,菱形的判定与性质
解:设BC交AE于G,AD交CF于H,如图所示:
∵四边形ABCD、四边形AECF是全等的矩形,
∴AB=CE,∠B=∠E=90°,AD∥BC,AE∥CF,
∴四边形AGCH是平行四边形,
在△ABG和△CEG中,
{∠AGB=∠CGE∠B=∠EAB=CE ,
∴△ABG≌△CEG(AAS),
∴AG=CG,
∴四边形AGCH是菱形,
设AG=CG=x,则BG=BC-CG=3-x,
在Rt△ABG中,由勾股定理得:12+(3-x)2=x2 ,
解得:x= 53 ,
∴CG= 53 ,
∴菱形AGCH的面积=CG ? AB= 53×1=53 ,
即图中重叠(阴影)部分的面积为 53 .
故答案为:C.
分析:证得四边形AGCH是平行四边形,由△ABG≌△CEG(AAS),证得四边形AGCH是菱形,设AG=CG=x,则BG=BC-CG=3-x,在Rt△ABG中,由勾股定理得出方程,解方程求得CG的长,即可求出菱形AGCH的面积.
5. B
考点:平行四边形的判定与性质,菱形的判定
解:过点A作 AE⊥BC 于E, AF⊥CD 于F,如图,
∵ 两条彩带宽度相同,
∴AB//CD , AD//BC , AE=AF .
∴ 四边形 ABCD 是平行四边形.
∵S?ABCD=BC?AE=CD?AF .
又 ∵AE=AF .
∴BC=CD ,
∴ 四边形 ABCD 是菱形.
故答案为: B .
分析:首先可判断重叠部分为平行四边形,且两条丝带宽度相同;再由平行四边形的面积可得邻边相等,则重叠部分为菱形.
6. C
考点:菱形的判定与性质,矩形的性质
解:∵CE∥BD,DE∥AC,
∴四边形CODE是平行四边形,
∵四边形ABCD是矩形,
∴AC=BD,OB=OD,OC=OA,∠ABC=90°
∴OC=OD,
∴四边形CODE是菱形
∵AB=4,BC=3
∴AC=AB2+BC2=5
∴OC= 52
∴四边形CODE的周长=4× 52 =10
故答案为:C.
分析:由矩形ABCD的对角线AC、BD相交于点O,CE∥BD,DE∥AC,易证得四边形CODE是菱形,又由AB=4,BC=3,可求得AC的长,继而求得OC的长,则可求得答案.
7. A
考点:角平分线的性质,勾股定理,平行四边形的判定,菱形的性质
解:连结EF,AE与BF交于点O,如图,
∵AO平分∠BAD,
∴∠1=∠2,
∵四边形ABCD为平行四边形,
∴AF∥BE,
∴∠1=∠3,
∴∠2=∠3,
∴AB=EB,
同理:AF=BE,
又∵AF∥BE,
∴四边形ABEF是平行四边形,
∴四边形ABEF是菱形,
∴AE⊥BF,OB=OF=6,OA=OE,
在Rt△AOB中,由勾股定理得:OA= AB2-OB2=102-62 =8,
∴AE=2OA=16.
故答案为:A.
分析:首先证明四边形ABEF是菱形,得出AE⊥BF,OB=OF=6,OA=OE,利用勾股定理计算出AO,从而得到AE的长.
8. A
考点:平行四边形的性质,菱形的判定
解:由题意知:四边形ABCD是平行四边形,
∴∠ADC=∠ABC,∠A=∠C,AD=BC,AB=CD,AB // CD
又∵DE,BF分别是∠ADC和∠ABC的平分线,
∴∠ADE=∠FBC,
在△ADE和△CBF中
{∠A=∠CAD=BC∠ADE=∠FBC
∴△ADE≌△CBF(ASA)
∴AE=CF,DE=BF
又∵AB=CD,AB // CD ,AE=CF
∴DF=BE,DF // BE、
∴四边形BFDE是平行四边形.
A、∵AB//CD,
∴∠AED=∠EDC,
又∵∠ADE=∠EDC,
∴∠ADE=∠AED,
∴AD=AE,
又∵∠A=60°,
∴△ADE是等边三角形,
∴AD=AE=DE,
无法判断平行四边形BFDE是菱形.
B、∵DE=DF,
∴平行四边形BFDE是菱形.
C、∵EF⊥BD,
∴平行四边形BFDE是菱形.
D、∵BD 是∠EDF的平分线,
∴∠EDB=∠FDB,
又∵DF//BE,
∴∠FDB=∠EBD,
∴∠EDB=∠EBD,
∴ED=DB,
∴平行四边形BFDE是菱形.
故答案为:A.
分析:先证明四边形BFDE是平行四边形,再根据菱形的判定定理逐项进行分析判断即可.
9. A
考点:菱形的判定
解:∵分别以A和B为圆心,大于 12 AB的长为半径画弧,两弧相交于C、D,
∴AC=AD=BD=BC,
∴四边形ADBC一定是菱形,
故答案为:A.
分析:根据垂直平分线的画法得出四边形ADBC四边的关系进而得出四边形一定是菱形.
10. D
考点:菱形的判定,矩形的判定
解:A、当AB=BC时,平行四边形ABCD为菱形,A选项不符合题意;
B、当AC⊥BD时,平行四边形ABCD为菱形, B选项不符合题意;
C、当∠ABC=90°时,平行四边形ABCD为矩形,故C选项不符合题意;
D、当AC=BD时,平行四边形ABCD为矩形,故D选项符合题意.
故答案为:D.
分析:根据矩形、菱形、正方形的的判定方法判断即可.
二、填空题
11. 12
考点:平行四边形的判定与性质,菱形的判定与性质
解:∵□ABCD
∴AD∥BC,AB∥CD
∴DE∥AF,∠AED=∠BAE
∵EF∥AD
∴四边形ADEF是平行四边形
∵AE平分∠BAD
∴∠DAE=∠BAE
∴∠AED=∠DAE
∴AD=DE
∴四边形ADEF是菱形
∵AB=5,CE=2,
∴DE=CD-CE=AB-CE=5-2=3
∴四边形ADEF的周长为3×4=12
故答案为:12.
分析:首先判定四边形ADEF是平行四边形,然后根据角平分线的性质得出AD=DE,进而判定四边形ADEF是菱形,即可求出其周长.
12. 6 3
考点:含30度角的直角三角形,勾股定理,菱形的判定与性质
解:过点B作BE⊥AD于点E,BF⊥CD于点F,
根据题意得:AD∥BC,AB∥CD,BE=BF=3,
∴四边形ABCD是平行四边形,
∵∠ABC=∠ADC=60°,
∴∠ABE=∠CBF=30°,
∴AB=2AE,BC=2CF,
∵AB2=AE2+BE2 ,
∴AB=2 3 ,
同理:BC=2 3 ,
∴AB=BC,
∴四边形ABCD是菱形,
∴AD=2 3 ,
∴S菱形ABCD=AD?BE=6 3 .
故答案为:6 3 .
分析:首先过点B作BE⊥AD于点E,BF⊥CD于点F,由题意可得四边形ABCD是平行四边形,继而求得AB=BC的长,判定四边形ABCD是菱形,则可求得答案.
13. 52;120
考点:菱形的判定与性质
解:∵AC与BD互相垂直且平分,BD=10,AC=24,
∴四边形ABCD是菱形,OD=5,OA=12
∴ AD=OA2+OD2=122+52=13
∴四边形的周长为AD×4=13×4=52
面积为 12×10×24=120 ;
故答案为52,120.
分析:根据AC与BD互相垂直且平分,BD=10,AC=24可知四边形ABCD是菱形,从而可求答案.
14. 6
考点:勾股定理,菱形的判定与性质
解:连结EF,AE与BF交于点O,
∵四边形ABCD是平行四边形,AB=AF,
∴四边形ABEF是菱形,
∴AE⊥BF,OB= 12 BF=4,OA= 12 AE.
∵AB=5,
在Rt△AOB中,AO= 52-42 =3,
∴AE=2AO=6.
故答案为:6.
分析:由基本作图得到AB=AF,AG平分∠BAD,故可得出四边形ABEF是菱形,由菱形的性质可知AE⊥BF,故可得出OB的长,再由勾股定理即可得出OA的长,进而得出结论.
三、解答题
15. 解: ∵ 四边形ABCD是平行四边形, AC=24,BD=10 ,
∴OA=12AC=12,OB=12BD=5 ,
∵ 在 △AOB 中, OA=12,OB=5,AB=13 ,
∴OA2+OB2=AB2 ,
∴△AOB 是直角三角形,且 ∠AOB=90° ,
∴AC⊥BD ,
∴ 四边形ABCD是菱形(对角线互相垂直的平行四边形是菱形).
考点:菱形的判定
分析:先根据平行四边形的性质可得 OA=12,OB=5 ,再根据勾股定理的逆定理可得 △AOB 是直角三角形,从而可得 AC⊥BD ,然后根据菱形的判定即可得证.
16. 解:∵DE∥AC,DF∥AB,
∴四边形AEDF是平行四边形,
∵AD平分∠BAC,
∴∠1=∠2(角平分线的定义),
∵DE∥AC,
∴∠2=∠3(两直线平行,内错角相等),
∴∠1=∠3(等量代换),
∴AE=DE,
∴平行四边形AEDF是菱形.
考点:菱形的判定
分析:先证明四边形AEDF是平行四边形,再根据角平分线的定义求出∠1=∠2,根据两直线平行,内错角相等求出∠2=∠3,然后求出∠1=∠3,根据等角对等边的性质可得AE=DE,然后根据邻边相等的平行四边形是菱形判定.
17. (1)解:能;嘉琪同学错在 AC 和 EF 并不是互相平分的, EF 垂直平分 AC ,
但未证明 AC 垂直平分 EF ,需要通过证明得出
(2)证明:∵四边形 ABCD 是平行四边形,
∴ AD//BC .
∴ ∠FAC=∠ECA .
∵ EF 是 AC 的垂直平分线,
∴ OA=OC .
∵∠AOF=∠EOC.
∴ ΔAOF≌ΔCOE(ASA) .
∴ EO=FO .
∴四边形AECF是平行四边形.
∵ AC 垂直平分 EF .
∴ EF 与 AC 互相垂直平分.
∴四边形 AECF 是菱形
考点:菱形的判定
分析:(1)题目中只说对角线 AC 的垂直平分线是 EF ,所以,只能得到EF垂直平分AC,并不能得到AC是平分EF的,所以不能说明四边形是平行四边形,故后面的结论不对,由此可知嘉琪的不符合题意;(2)根据 EF 是 AC 的垂直平分线,所以 OA=OC ,由 AD//BC .推出 ∠FAC=∠ECA ,再结合对顶角,证明 ΔAOF≌ΔCOE ,可证四边形是平行四边形,最后根据对角线互相垂直,可证明菱形.
18. (1)证明∵四边形ABCD是矩形,
∴AB=CD,AD=BC,∠A=∠C=90°,
∵在矩形ABCD中,M、N分别是AD、BC的中点,
∴AM= 12 AD,CN= 12 BC,
∴AM=CN,
在△MAB和△NDC中,
∵AB=CD,∠A=∠C=90°,AM=CN
∴△MBA≌△NDC(SAS)
(2)解:四边形MPNQ是菱形.
理由如下:连接AP,MN,
则四边形ABNM是矩形,
∵AN和BM互相平分,
则A,P,N在同一条直线上,
易证:△ABN≌△BAM,
∴AN=BM,
∵△MAB≌△NDC,
∴BM=DN,
∵P、Q分别是BM、DN的中点,
∴PM=NQ,
∵DM=BN,∠MDQ=∠NBP,DQ=BP,
∴△MQD≌△NPB(SAS).
∴四边形MPNQ是平行四边形,
∵M是AD中点,Q是DN中点,
∴MQ= 12 AN,MQ= 12 BM,
∵MP= 12 BM
∴MP=MQ,
∴平行四边形MQNP为菱形.
考点:三角形全等及其性质,三角形全等的判定,菱形的判定,矩形的性质
分析:(1)根据矩形的性质和中点的定义,利用SAS判定△MBA≌△NDC;(2)四边形MPNQ是菱形,连接AN,由(1)可得到BM=DN,再有中点得到PM=NQ,再通过证明△MQD≌△NPB得到MQ=PN,从而证明四边形MPNQ是平行四边形,利用三角形中位线的性质可得:MP=MQ,进而证明四边形MQNP是菱形.
19. (1)解:根据题意可得: {y=-2x+8y=12x+3 ,
解得: {x=2y=4 ,
∴点D坐标(2,4)
(2)解:∵直线y=﹣2x+8分别交x轴,y轴于点A,B,
∴点B(0,8),点A(4,0).
∵直线y =12 x+3交y轴于点C,
∴点C(0,3).
∵AE∥y轴交直线y =12 x+3于点E,
∴点E(4,5)
∵点B(0,8),点A(4,0),点C(0,3),点E(4,5),
∴BC=5,AE=5,AC =42+32= 5,BE =42+(8-5)2= 5,
∴BC=AE=AC=BE,
∴四边形ACBE是菱形
(3)解:∵BC=AC,
∴∠ABC=∠CAB.
∵∠CGF=∠ABC,∠AGF=∠ABC+∠BFG=∠AGC+∠CGF,
∴∠AGC=∠BFG,且FG=CG,∠ABC=∠CAB,
∴△ACG≌△BGF(AAS),
∴BG=AC=5,
设点G(a,﹣2a+8),
∴(﹣2a+8﹣8)2+(a﹣0)2=52 ,
∴a=± 5 ,
∵点G在线段AB上,
∴a =5 ,
∴点G( 5 ,8﹣2 5 )
考点:两一次函数图象相交或平行问题,三角形全等及其性质,三角形全等的判定,菱形的判定
分析:(1)两个解析式组成方程组,可求交点D坐标;?(2)先求出点A,点B,点E,点C坐标,由两点距离公式可求BC=AE=AC=BE=5,可证四边形ACBE是菱形;?(3)由“AAS”可证△ACG≌△BGF,可得BG=AC=5,由两点距离公式可求点G坐标.
一、单选题
1.如图,四边形ABCD沿直线l对折后重合,如果 AD//BC ,则结论①AB // CD;②AB=CD;③ AB⊥BC ;④ AO=OC 中正确的是(? )
A.?1个???????????????????????????????????????B.?2个???????????????????????????????????????C.?3个???????????????????????????????????????D.?4个
2.如图,在 △ABC 中,点D在边BC上,过点D作 DE//AC , DF//AB ,分别交AB,AC于E,F两点.则下列命题是假命题的是(??? )
A.?四边形 AEDF 是平行四边形?????????????????????????B.?若 ∠B+∠C=90° ,则四边形 AEDF 是矩形
C.?若 BD=CD ,则四边形 AEDF 是菱形???????D.?若 AD=BD ,则四边形 AEDF 是矩形
3.如图,在平行四边形ABCD中,点F是AB的中点,连接DF并延长,交CB的延长线于点E , 连接AE . 添加一个条件,使四边形AEBD是菱形,这个条件是(?? )
A.?∠BAD=∠BDA?????????????????B.?AB=DE?????????????????C.?DF=EF?????????????????D.?DE平分 ∠ADB
4.两张全等的矩形纸片 ABCD,AECF 按如图方式交叉叠放在一起,AB=AF,AE=BC.若 AB=1,BC=3,则图中重叠(阴影)部分的面积为(?? ).
A.?2?????????????????????????????????????????B.?3?????????????????????????????????????????C.?53?????????????????????????????????????????D.?43
5.某班同学在“为抗疫英雄祈福”的主题班会课上制作象征“平安归来”的黄丝带,如图所示,丝带重叠部分形成的图形是(?? )
A.?矩形?????????????????????????????????B.?菱形?????????????????????????????????C.?正方形?????????????????????????????????D.?等腰梯形
6.如图,矩形ABCD的对角线AC、BD相交于点O,CE∥BD,DE∥AC,若AB=4,BC=3,则四边形CODE的周长是( )
A.?5??????????????????????????????????????????B.?8??????????????????????????????????????????C.?10??????????????????????????????????????????D.?12
7.如图,在?ABCD中,用直尺和圆规作∠BAD的平分线AG交BC于点E.若BF=12,AB=10,则AE的长为(??? )
A.?16?????????????????????????????????????????B.?15?????????????????????????????????????????C.?14?????????????????????????????????????????D.?13
8.如图,在 ? ABCD中,DE,BF分别是∠ADC和∠ABC的平分线,添加一个条件,仍无法判断四边形BFDE为菱形的是(??? )
A.?∠A=60????????????????????????B.?DE=DF???????????????????????C.?EF⊥BD???????????????????????D.?BD 是∠EDF的平分线
9.如图,某同学作线段AB的垂直平分线:分别以点A和点B为圆心,大于 12 AB的长为半径画弧,两弧相交于点C,D,则直线CD为线段AB的垂直平分线.根据这个同学的作图方法可知四边形ADBC一定是(?? )
A.?菱形?????????????????????????????B.?平行四边形?????????????????????????????C.?矩形?????????????????????????????D.?一般的四边形
10.已知四边形ABCD是平行四边形,下列结论错误的是(??? )
A.?当AB=BC时,它是菱形??????????????????????????????????????B.?当AC⊥BD时,它是菱形
C.?当 ∠ABC=90? 时,它是矩形??????????????????????????D.?当 AC=BD 时,它是菱形
二、填空题
11.如图,在□ABCD中,以点A为圆心,以任意长为半径画圆弧,分别交边AD、AB于点M、N , 再分别以点M、N为圆心,以大于 12MN 长为半径画圆弧,两弧交于点P , 作射线AP交边CD于点E , 过点E作EF∥AD交AB于点F . 若AB=5,CE=2,则四边形ADEF的周长为________.
12.如图,小华剪了两条宽为3的纸条,交叉叠放在一起,且它们较小的交角为60°,则它们重叠部分的面积为________.
13.如图,在四边形ABCD中,对角线AC,BD交于点O,AC与BD互相垂直且平分,BD=10,AC=24,则四边形周长为________,面积为________.
14.如图,在?ABCD中,用直尺和圆规作∠BAD的平分线AG交BC于点E.若BF=8,AB=5,则AE的长为________.
三、解答题
15.如图,平行四边形ABCD的对角线交于点O,且AB=13,AC=24,BD=10.求证:四边形ABCD是菱形.
16.已知:如图,在△ABC中,AD是∠BAC的平分线,DE∥AC,DF∥AB.求证:四边形AEDF是菱形.
17.老师布置了一个作业,如下:
已知:如图1 ?ABCD 的对角线 AC 的垂直平分线 EF 交 AD 于点 F ,交 BC 于点 E ,交 AC 于点 O .求证:四边形 AECF 是菱形.
嘉琪同学写出了如图2所示的证明过程,老师说嘉琪同学的作业是错误的.请你解答下列问题:
(1)能找出该同学错误的原因吗?请你指出来;
(2)请你给出本题的符合题意证明过程.
18.如图,在矩形ABCD中,M、N分别是AD、BC的中点,P、Q分别是BM、DN的中点.
(1)求证:△MBA≌△NDC;
(2)四边形MPNQ是什么样的特殊四边形?不用证明.
19.如图,直线y=﹣2x+8分别交x轴,y轴于点A , B , 直线y =12 x+3交y轴于点C , 两直线相交于点D .
(1)求点D的坐标;
(2)如图2,过点A作AE∥y轴交直线y =12 x+3于点E , 连接AC , BE . 求证:四边形ACBE是菱形;
(3)如图3,在(2)的条件下,点F在线段BC上,点G在线段AB上,连接CG , FG , 当CG=FG , 且∠CGF=∠ABC时,求点G的坐标.
答案解析部分
一、单选题
1. C
考点:菱形的判定与性质,轴对称的性质
解:如图所示:
∵直线l是四边形ABCD的对称轴,
∴AB=AD,BC=DC,∠1=∠2,∠3=∠4,
又∵AD∥BC,
∴∠2=∠3,
∴∠1=∠4,
∴AB∥CD,故①正确;
∴四边形ABCD是菱形;
∴AB=CD,故②正确;
∵四边形ABCD是菱形;
∴AO=OC,故④正确.
∵当四边形ABCD是菱形时,直线l是四边形ABCD的对称轴,但是AB与BC不一定垂直,故③错误.
故答案为:C.
分析:根据轴对称图形的性质得出AB=AD,BC=DC,∠1=∠2,∠3=∠4,根据平行线的性质得出∠2=∠3,根据等量代换得出∠1=∠4,进而根据内错角相等,二直线平行得出AB∥CD,根据一组邻边相等且两组对边分别平行的四边形是菱形得出四边形ABCD是菱形,进而根据菱形的性质即可一一判断得出答案.
2. C
考点:平行四边形的判定,菱形的判定,矩形的判定
解: ∵ DE//AC,DF//AB
∴ 四边形AEDF是平行四边形,故A选项不符合题意;
∵ 四边形AEDF是平行四边形, ∠B+∠C=90°
∴∠BAC=90°
∴ 四边形AEDF是矩形,故B选项不符合题意;
∵DE//AC
∴DEAC=BDBC=12
∴DE=12AC
同理 DF=12AB
要想四边形AEDF是菱形,只需 DE=DF ,则需 AC=AB 显然没有这个条件,故C选项符合题意;
∵AD=BD ,则 ∠B=∠DAB , ∠DAC=∠C ,
∵∠B+∠C+∠BAC=180°
∴∠BAC=90°
∴ ∴ 四边形AEDF是矩形,故D选项不符合题意;
故答案为:C.
分析:根据平行四边形、矩形、菱形的判定逐项判定即可。
3. D
考点:菱形的判定
解:在平行四边形ABCD中,AD∥BC,
∴∠DAB=∠EBA,
∵点F是AB的中点,
∴AF=BF,
∵∠AFD=∠BFE,
∴△ADF≌△BEF,
∴AD=BE,
∵AD∥BE,
∴四边形AEBD是平行四边形,
A、当 ∠BAD=∠BDA 时,得到AB=BD,无法判定四边形AEBD是菱形,故该选项不符合题意;
B、AB=BE时,无法判定四边形AEBD是菱形,故该选项不符合题意;
C、DF=EF时,无法判定四边形AEBD是菱形,故该选项不符合题意;
D、当DE平分 ∠ADB 时,四边形AEBD是菱形,故该选项符合题意;
故答案为:D.
分析:先证明△ADF≌△BEF,得到AD=BE,推出四边形AEBD是平行四边形,再逐项分析即可。
4. C
考点:勾股定理,菱形的判定与性质
解:设BC交AE于G,AD交CF于H,如图所示:
∵四边形ABCD、四边形AECF是全等的矩形,
∴AB=CE,∠B=∠E=90°,AD∥BC,AE∥CF,
∴四边形AGCH是平行四边形,
在△ABG和△CEG中,
{∠AGB=∠CGE∠B=∠EAB=CE ,
∴△ABG≌△CEG(AAS),
∴AG=CG,
∴四边形AGCH是菱形,
设AG=CG=x,则BG=BC-CG=3-x,
在Rt△ABG中,由勾股定理得:12+(3-x)2=x2 ,
解得:x= 53 ,
∴CG= 53 ,
∴菱形AGCH的面积=CG ? AB= 53×1=53 ,
即图中重叠(阴影)部分的面积为 53 .
故答案为:C.
分析:证得四边形AGCH是平行四边形,由△ABG≌△CEG(AAS),证得四边形AGCH是菱形,设AG=CG=x,则BG=BC-CG=3-x,在Rt△ABG中,由勾股定理得出方程,解方程求得CG的长,即可求出菱形AGCH的面积.
5. B
考点:平行四边形的判定与性质,菱形的判定
解:过点A作 AE⊥BC 于E, AF⊥CD 于F,如图,
∵ 两条彩带宽度相同,
∴AB//CD , AD//BC , AE=AF .
∴ 四边形 ABCD 是平行四边形.
∵S?ABCD=BC?AE=CD?AF .
又 ∵AE=AF .
∴BC=CD ,
∴ 四边形 ABCD 是菱形.
故答案为: B .
分析:首先可判断重叠部分为平行四边形,且两条丝带宽度相同;再由平行四边形的面积可得邻边相等,则重叠部分为菱形.
6. C
考点:菱形的判定与性质,矩形的性质
解:∵CE∥BD,DE∥AC,
∴四边形CODE是平行四边形,
∵四边形ABCD是矩形,
∴AC=BD,OB=OD,OC=OA,∠ABC=90°
∴OC=OD,
∴四边形CODE是菱形
∵AB=4,BC=3
∴AC=AB2+BC2=5
∴OC= 52
∴四边形CODE的周长=4× 52 =10
故答案为:C.
分析:由矩形ABCD的对角线AC、BD相交于点O,CE∥BD,DE∥AC,易证得四边形CODE是菱形,又由AB=4,BC=3,可求得AC的长,继而求得OC的长,则可求得答案.
7. A
考点:角平分线的性质,勾股定理,平行四边形的判定,菱形的性质
解:连结EF,AE与BF交于点O,如图,
∵AO平分∠BAD,
∴∠1=∠2,
∵四边形ABCD为平行四边形,
∴AF∥BE,
∴∠1=∠3,
∴∠2=∠3,
∴AB=EB,
同理:AF=BE,
又∵AF∥BE,
∴四边形ABEF是平行四边形,
∴四边形ABEF是菱形,
∴AE⊥BF,OB=OF=6,OA=OE,
在Rt△AOB中,由勾股定理得:OA= AB2-OB2=102-62 =8,
∴AE=2OA=16.
故答案为:A.
分析:首先证明四边形ABEF是菱形,得出AE⊥BF,OB=OF=6,OA=OE,利用勾股定理计算出AO,从而得到AE的长.
8. A
考点:平行四边形的性质,菱形的判定
解:由题意知:四边形ABCD是平行四边形,
∴∠ADC=∠ABC,∠A=∠C,AD=BC,AB=CD,AB // CD
又∵DE,BF分别是∠ADC和∠ABC的平分线,
∴∠ADE=∠FBC,
在△ADE和△CBF中
{∠A=∠CAD=BC∠ADE=∠FBC
∴△ADE≌△CBF(ASA)
∴AE=CF,DE=BF
又∵AB=CD,AB // CD ,AE=CF
∴DF=BE,DF // BE、
∴四边形BFDE是平行四边形.
A、∵AB//CD,
∴∠AED=∠EDC,
又∵∠ADE=∠EDC,
∴∠ADE=∠AED,
∴AD=AE,
又∵∠A=60°,
∴△ADE是等边三角形,
∴AD=AE=DE,
无法判断平行四边形BFDE是菱形.
B、∵DE=DF,
∴平行四边形BFDE是菱形.
C、∵EF⊥BD,
∴平行四边形BFDE是菱形.
D、∵BD 是∠EDF的平分线,
∴∠EDB=∠FDB,
又∵DF//BE,
∴∠FDB=∠EBD,
∴∠EDB=∠EBD,
∴ED=DB,
∴平行四边形BFDE是菱形.
故答案为:A.
分析:先证明四边形BFDE是平行四边形,再根据菱形的判定定理逐项进行分析判断即可.
9. A
考点:菱形的判定
解:∵分别以A和B为圆心,大于 12 AB的长为半径画弧,两弧相交于C、D,
∴AC=AD=BD=BC,
∴四边形ADBC一定是菱形,
故答案为:A.
分析:根据垂直平分线的画法得出四边形ADBC四边的关系进而得出四边形一定是菱形.
10. D
考点:菱形的判定,矩形的判定
解:A、当AB=BC时,平行四边形ABCD为菱形,A选项不符合题意;
B、当AC⊥BD时,平行四边形ABCD为菱形, B选项不符合题意;
C、当∠ABC=90°时,平行四边形ABCD为矩形,故C选项不符合题意;
D、当AC=BD时,平行四边形ABCD为矩形,故D选项符合题意.
故答案为:D.
分析:根据矩形、菱形、正方形的的判定方法判断即可.
二、填空题
11. 12
考点:平行四边形的判定与性质,菱形的判定与性质
解:∵□ABCD
∴AD∥BC,AB∥CD
∴DE∥AF,∠AED=∠BAE
∵EF∥AD
∴四边形ADEF是平行四边形
∵AE平分∠BAD
∴∠DAE=∠BAE
∴∠AED=∠DAE
∴AD=DE
∴四边形ADEF是菱形
∵AB=5,CE=2,
∴DE=CD-CE=AB-CE=5-2=3
∴四边形ADEF的周长为3×4=12
故答案为:12.
分析:首先判定四边形ADEF是平行四边形,然后根据角平分线的性质得出AD=DE,进而判定四边形ADEF是菱形,即可求出其周长.
12. 6 3
考点:含30度角的直角三角形,勾股定理,菱形的判定与性质
解:过点B作BE⊥AD于点E,BF⊥CD于点F,
根据题意得:AD∥BC,AB∥CD,BE=BF=3,
∴四边形ABCD是平行四边形,
∵∠ABC=∠ADC=60°,
∴∠ABE=∠CBF=30°,
∴AB=2AE,BC=2CF,
∵AB2=AE2+BE2 ,
∴AB=2 3 ,
同理:BC=2 3 ,
∴AB=BC,
∴四边形ABCD是菱形,
∴AD=2 3 ,
∴S菱形ABCD=AD?BE=6 3 .
故答案为:6 3 .
分析:首先过点B作BE⊥AD于点E,BF⊥CD于点F,由题意可得四边形ABCD是平行四边形,继而求得AB=BC的长,判定四边形ABCD是菱形,则可求得答案.
13. 52;120
考点:菱形的判定与性质
解:∵AC与BD互相垂直且平分,BD=10,AC=24,
∴四边形ABCD是菱形,OD=5,OA=12
∴ AD=OA2+OD2=122+52=13
∴四边形的周长为AD×4=13×4=52
面积为 12×10×24=120 ;
故答案为52,120.
分析:根据AC与BD互相垂直且平分,BD=10,AC=24可知四边形ABCD是菱形,从而可求答案.
14. 6
考点:勾股定理,菱形的判定与性质
解:连结EF,AE与BF交于点O,
∵四边形ABCD是平行四边形,AB=AF,
∴四边形ABEF是菱形,
∴AE⊥BF,OB= 12 BF=4,OA= 12 AE.
∵AB=5,
在Rt△AOB中,AO= 52-42 =3,
∴AE=2AO=6.
故答案为:6.
分析:由基本作图得到AB=AF,AG平分∠BAD,故可得出四边形ABEF是菱形,由菱形的性质可知AE⊥BF,故可得出OB的长,再由勾股定理即可得出OA的长,进而得出结论.
三、解答题
15. 解: ∵ 四边形ABCD是平行四边形, AC=24,BD=10 ,
∴OA=12AC=12,OB=12BD=5 ,
∵ 在 △AOB 中, OA=12,OB=5,AB=13 ,
∴OA2+OB2=AB2 ,
∴△AOB 是直角三角形,且 ∠AOB=90° ,
∴AC⊥BD ,
∴ 四边形ABCD是菱形(对角线互相垂直的平行四边形是菱形).
考点:菱形的判定
分析:先根据平行四边形的性质可得 OA=12,OB=5 ,再根据勾股定理的逆定理可得 △AOB 是直角三角形,从而可得 AC⊥BD ,然后根据菱形的判定即可得证.
16. 解:∵DE∥AC,DF∥AB,
∴四边形AEDF是平行四边形,
∵AD平分∠BAC,
∴∠1=∠2(角平分线的定义),
∵DE∥AC,
∴∠2=∠3(两直线平行,内错角相等),
∴∠1=∠3(等量代换),
∴AE=DE,
∴平行四边形AEDF是菱形.
考点:菱形的判定
分析:先证明四边形AEDF是平行四边形,再根据角平分线的定义求出∠1=∠2,根据两直线平行,内错角相等求出∠2=∠3,然后求出∠1=∠3,根据等角对等边的性质可得AE=DE,然后根据邻边相等的平行四边形是菱形判定.
17. (1)解:能;嘉琪同学错在 AC 和 EF 并不是互相平分的, EF 垂直平分 AC ,
但未证明 AC 垂直平分 EF ,需要通过证明得出
(2)证明:∵四边形 ABCD 是平行四边形,
∴ AD//BC .
∴ ∠FAC=∠ECA .
∵ EF 是 AC 的垂直平分线,
∴ OA=OC .
∵∠AOF=∠EOC.
∴ ΔAOF≌ΔCOE(ASA) .
∴ EO=FO .
∴四边形AECF是平行四边形.
∵ AC 垂直平分 EF .
∴ EF 与 AC 互相垂直平分.
∴四边形 AECF 是菱形
考点:菱形的判定
分析:(1)题目中只说对角线 AC 的垂直平分线是 EF ,所以,只能得到EF垂直平分AC,并不能得到AC是平分EF的,所以不能说明四边形是平行四边形,故后面的结论不对,由此可知嘉琪的不符合题意;(2)根据 EF 是 AC 的垂直平分线,所以 OA=OC ,由 AD//BC .推出 ∠FAC=∠ECA ,再结合对顶角,证明 ΔAOF≌ΔCOE ,可证四边形是平行四边形,最后根据对角线互相垂直,可证明菱形.
18. (1)证明∵四边形ABCD是矩形,
∴AB=CD,AD=BC,∠A=∠C=90°,
∵在矩形ABCD中,M、N分别是AD、BC的中点,
∴AM= 12 AD,CN= 12 BC,
∴AM=CN,
在△MAB和△NDC中,
∵AB=CD,∠A=∠C=90°,AM=CN
∴△MBA≌△NDC(SAS)
(2)解:四边形MPNQ是菱形.
理由如下:连接AP,MN,
则四边形ABNM是矩形,
∵AN和BM互相平分,
则A,P,N在同一条直线上,
易证:△ABN≌△BAM,
∴AN=BM,
∵△MAB≌△NDC,
∴BM=DN,
∵P、Q分别是BM、DN的中点,
∴PM=NQ,
∵DM=BN,∠MDQ=∠NBP,DQ=BP,
∴△MQD≌△NPB(SAS).
∴四边形MPNQ是平行四边形,
∵M是AD中点,Q是DN中点,
∴MQ= 12 AN,MQ= 12 BM,
∵MP= 12 BM
∴MP=MQ,
∴平行四边形MQNP为菱形.
考点:三角形全等及其性质,三角形全等的判定,菱形的判定,矩形的性质
分析:(1)根据矩形的性质和中点的定义,利用SAS判定△MBA≌△NDC;(2)四边形MPNQ是菱形,连接AN,由(1)可得到BM=DN,再有中点得到PM=NQ,再通过证明△MQD≌△NPB得到MQ=PN,从而证明四边形MPNQ是平行四边形,利用三角形中位线的性质可得:MP=MQ,进而证明四边形MQNP是菱形.
19. (1)解:根据题意可得: {y=-2x+8y=12x+3 ,
解得: {x=2y=4 ,
∴点D坐标(2,4)
(2)解:∵直线y=﹣2x+8分别交x轴,y轴于点A,B,
∴点B(0,8),点A(4,0).
∵直线y =12 x+3交y轴于点C,
∴点C(0,3).
∵AE∥y轴交直线y =12 x+3于点E,
∴点E(4,5)
∵点B(0,8),点A(4,0),点C(0,3),点E(4,5),
∴BC=5,AE=5,AC =42+32= 5,BE =42+(8-5)2= 5,
∴BC=AE=AC=BE,
∴四边形ACBE是菱形
(3)解:∵BC=AC,
∴∠ABC=∠CAB.
∵∠CGF=∠ABC,∠AGF=∠ABC+∠BFG=∠AGC+∠CGF,
∴∠AGC=∠BFG,且FG=CG,∠ABC=∠CAB,
∴△ACG≌△BGF(AAS),
∴BG=AC=5,
设点G(a,﹣2a+8),
∴(﹣2a+8﹣8)2+(a﹣0)2=52 ,
∴a=± 5 ,
∵点G在线段AB上,
∴a =5 ,
∴点G( 5 ,8﹣2 5 )
考点:两一次函数图象相交或平行问题,三角形全等及其性质,三角形全等的判定,菱形的判定
分析:(1)两个解析式组成方程组,可求交点D坐标;?(2)先求出点A,点B,点E,点C坐标,由两点距离公式可求BC=AE=AC=BE=5,可证四边形ACBE是菱形;?(3)由“AAS”可证△ACG≌△BGF,可得BG=AC=5,由两点距离公式可求点G坐标.
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
