5.2.1 菱形的性质同步练习(含解析)
文档属性
| 名称 | 5.2.1 菱形的性质同步练习(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 278.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-11 17:44:03 | ||
图片预览




文档简介
初中数学浙教版八年级下册5.2.1菱形的性质 同步练习
一、单选题
1.下面性质中,菱形不一定具备的是(?? )
A.?四条边都相等???????????????B.?每一条对角线平分一组对角???????????????C.?邻角互补???????????????D.?对角线相等
2.如图,在菱形ABCD中,对角线AC, BD相交于点O.下列结论不一定成立的是 (??? )
A.?BD平分∠ADC??????????????????????????B.?AC=BD??????????????????????????C.?AC⊥BD??????????????????????????D.?OA=OC
3.下列性质中,菱形对角线不具有的是(?? )
A.?对角线互相垂直???????????B.?对角线所在直线是对称轴???????????C.?对角线相等???????????D.?对角线互相平分
4.已知菱形 ABCD 中,对角线 AC 与 BD 交于点O, BD=10 , AC=24 ,则该菱形的周长是(?? )
A.?13???????????????????????????????????????B.?52???????????????????????????????????????C.?120???????????????????????????????????????D.?240
5.若菱形的两条对角线长分别为8和6,则这个菱形的面积是(?? )
A.?96?????????????????????????????????????????B.?48?????????????????????????????????????????C.?24?????????????????????????????????????????D.?12
6.菱形 ABCD 的边长是 5cm ,一条对角线 AC 的长是 8cm ,则此菱形的面积为(?? )
A.?40cm2??????????????????????????????B.?48cm2??????????????????????????????C.?243cm2??????????????????????????????D.?24cm2
7.如图,菱形 ABCD 中, ∠A=50° ,则 ∠ADB 的度数为(?? )
A.?65°????????????????????????????????????B.?55°????????????????????????????????????C.?45°????????????????????????????????????D.?25°
8.菱形的一个内角是 60° ,边长是 3cm ,则这个菱形的较短的对角线长是(???? )
A.?32cm????????????????????????????????B.?323cm????????????????????????????????C.?3cm????????????????????????????????D.?33cm
9.数轴上两点A、C表示的数分别为-2,6,以 AC 为对角线做菱形 ABCD ,连接 BD 交 AC 于O点,则O点所表示的数为( )
A.?-1??????????????????????????????????????????B.?1??????????????????????????????????????????C.?2??????????????????????????????????????????D.?3
10.菱形的两条对角线把菱形分成全等的直角三角形的个数是( )
A.?1个???????????????????????????????????????B.?2个???????????????????????????????????????C.?3个???????????????????????????????????????D.?4个
二、填空题
11.一个菱形的边长是 5cm ,一条对角线长 6cm ,则此菱形的面积为________ cm2 .
12.若菱形的面积为24,一条对角线长为8,则另一条对角线长为________,边长为________.
13.菱形的两条对角线分别是12和16,则此菱形的边长是________.
14.如图,在菱形ABCD中,AB=6,∠B=60°,点G是边CD边的中点,点E、F分别是AG、AD上的两个动点,则EF+ED的最小值是________.
15.如图,在边长为10的菱形 ABCD 中,对角线 BD=16 ,点O是线段 BD 上的动点, OE⊥AB 于E, OF⊥AD 于F.则 OE+OF= ________.
三、解答题
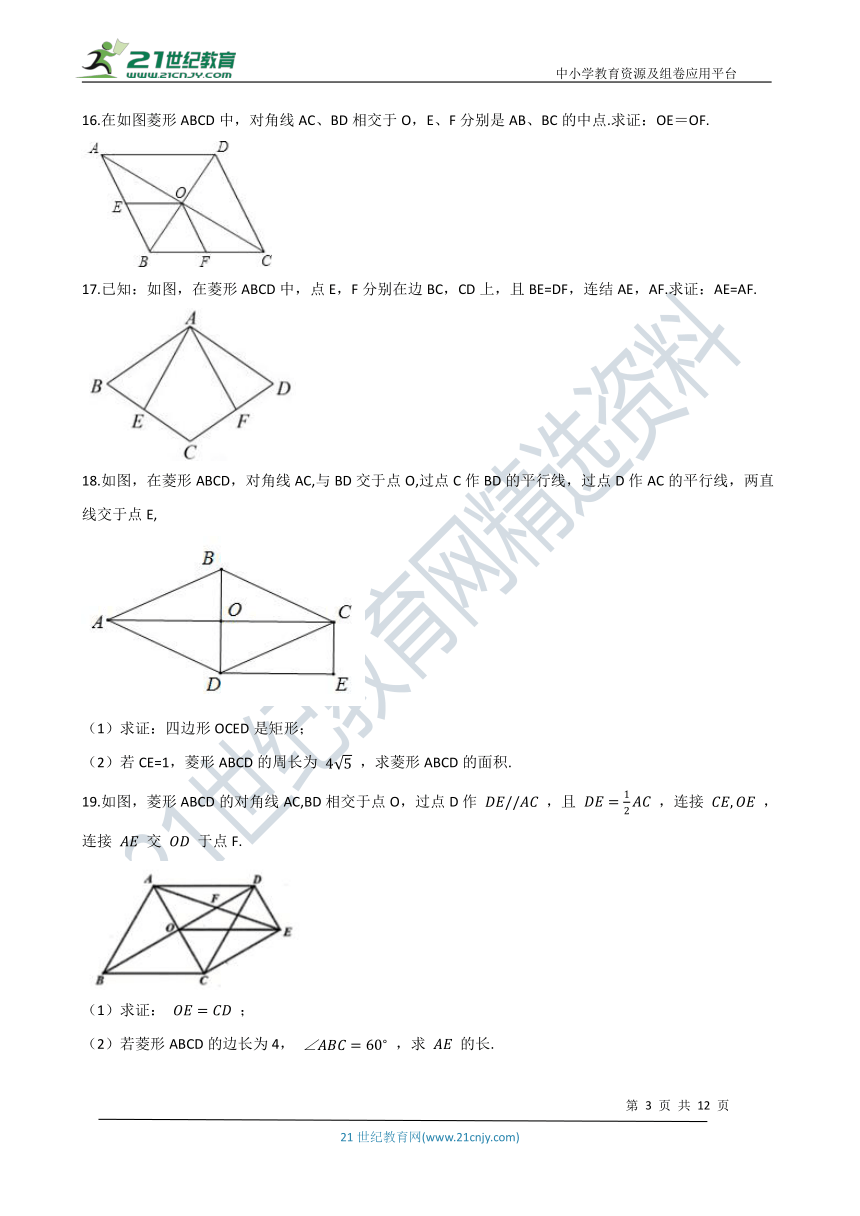
16.在如图菱形ABCD中,对角线AC、BD相交于O,E、F分别是AB、BC的中点.求证:OE=OF.
17.已知:如图,在菱形ABCD中,点E,F分别在边BC,CD上,且BE=DF,连结AE,AF.求证:AE=AF.
18.如图,在菱形ABCD,对角线AC,与BD交于点O,过点C作BD的平行线,过点D作AC的平行线,两直线交于点E,
(1)求证:四边形OCED是矩形;
(2)若CE=1,菱形ABCD的周长为 45 ,求菱形ABCD的面积.
19.如图,菱形ABCD的对角线AC,BD相交于点O,过点D作 DE//AC ,且 DE=12AC ,连接 CE,OE ,连接 AE 交 OD 于点F.
(1)求证: OE=CD ;
(2)若菱形ABCD的边长为4, ∠ABC=60? ,求 AE 的长.
答案解析部分
一、单选题
1. D
考点:菱形的性质
解:A. 菱形的四条边都相等,说法正确,不符合题意;
B. 菱形的每一条对角线平分一组对角,说法正确,不符合题意;
C. 菱形的邻角互补,说法正确,不符合题意;
D. 菱形的对角线不一定相等,说法不正确,符合题意.
故答案为:D.
分析:根据菱形的性质即可得出答案.
2. B
考点:菱形的性质
解:∵四边形ABCD是菱形,
∴BD平分∠ADC,OA=OC,AC⊥BD,
无法得出AC=BD,
B符合题意,选项A、C、D不符合题意,
故答案为:B.
分析:利用菱形的性质邻边相等、对角线互相垂直且平分进而分析即可.
3.C
考点:菱形的性质
解:∵菱形对角线具有的性质有:对角线互相垂直,对角线互相平分, ∴对角线所在直线是对称轴.
故A,B,D正确,C错误.
故选C.
分析:由菱形的对角线互相平分且垂直,可得菱形对角线所在直线是对称轴,继而求得答案.
4. B
考点:菱形的性质
解:∵菱形ABCD中,BD=10,AC=24,
∴OB=5,OA=12,∠AOB=90°
在Rt△ABO中,AB= 52+122 =13,
∴菱形ABCD的周长=4AB=52.
故答案为:B.
分析:由菱形的对角线垂直且互相平分得出OB=5,OA=12,∠AOB=90°,从而利用勾股定理算出AB的长,继而求得菱形ABCD的周长.
5. C
考点:菱形的性质
解:∵四边形ABCD是菱形,
∴S= 12 ×6×8=24.
故答案为:C.
分析:根据菱形的面积等于对角线乘积的一半计算即可.
6. D
考点:菱形的性质
解:根据题意画出图形,如图所示:
∵ 四边形 ABCD 是菱形,
∴AB=BC=CD=AD=5cm , AC⊥BD , OA=OC , OB=OD ,
又 AC 的长是 8cm ,
∴OA=4cm ,
∴OB=AB2-OA2=52-42=3cm ,
∴BD=6cm ,
∴ 菱形的面积 =12AC·BD=12×8×6=24cm2 .
故答案为:D.
分析:根据菱形 ABCD 的边长是 5cm ,一条对角线 AC 的长是 8cm ,可以求出另一条对角线的长度是 6cm ,利用菱形的面积等于 12AC·BD 可求出结果.
7. A
考点:菱形的性质
解:∵四边形ABCD为菱形,∴AD=AB,
∴∠ADB=∠ABD=(180°-∠A)÷2=(180°-50°)÷2=65°,
故答案为:A.
分析:由菱形的性质可得AD=AB,于是根据等边对等角可得∠ADB=∠ABD,然后由三角形内角和定理可求解.
8. C
考点:菱形的性质
解:因为菱形的四边相等,当一个内角是60°,则较短对角线与两边组成等边三角形.
∵菱形的边长是 3cm ,
∴这个菱形的较短的对角线长是3cm.
故答案为:C.
分析:根据 菱形的一个内角是?60°? , 边长是?3cm ,进行求解即可。
9. C
考点:菱形的性质
解:AC=6-(-2)=8
以 AC 为对角线做菱形 ABCD ,连接 BD 交 AC 于O点,
AO=CO=4,
O点表示数为:-2+4=2,
故答案为:C.
分析:先确定AC的长,然后由菱形的性质,对角线互相平分求出AO的长,利用A点坐标加AO即可.
10. D
考点:菱形的性质
解:如图所示:
∵AC,BD是菱形的对角线,
∴AC⊥BD,且DE=BE,AE=CE,
∵AD=CD=BC=AB,
∴在Rt△ADE和Rt△ABE中, {AD=ABAE=AE ,
∴Rt△ADE≌Rt△ABE(HL),
同理可得出Rt△ADE≌Rt△CDE,Rt△CDE≌Rt△CBE,Rt△ABE≌Rt△CBE.
∴Rt△ADE≌Rt△CDE≌Rt△ABE≌Rt△CBE,
∴菱形中两条对角线把菱形分成全等中直角三角形的个数是4个,
故答案为:D.
分析:利用菱形的性质得出对角线垂直且互相平分,且4条边相等,即可得到全等的直角三角形的个数是4个.
二、填空题
11. 24
考点:菱形的性质
解:如图, AB=5cm,AC=6cm ,
∵四边形ABCD是菱形,
∴ AO=12AC=3cm,OB=12BD,AC⊥BD ,
∴∠AOB=90° ?,
∴BO=AB2-AO2=4cm ,
∴BD=2OB=8cm ,
∴S=12AC?BD=12×6×8=24cm2 ,
故答案为:24.
分析:首先根据菱形的性质和勾股定理求出另一条对角线的长度,然后利用菱形的面积公式求解即可.
12. 6;5
考点:菱形的性质
解:如图:
∵菱形ABCD的面积为24
∴ 12 AC·BD=24,
∵AC=8,
∴BD=6;
∵四边形ABCD是菱形,
∴AB=BC=CD=DA,AC⊥BD,
∴OA= 12 AC=4,OB= 12 BD=3,
∴AB= OA2+OB2=32+42 =5.
故答案为6,5.
分析:根菱形面积等于对角线积的一半,即可求得另一条对角线的长度,然后根据勾股定理即可求得菱形的边长.
13. 10
考点:菱形的性质
解:如图,
∵菱形ABCD中,AC=12,BD=16,
∴OA= 12 AC=6,OB= 12 BD=8,AC⊥BD,
∴AB= OA2+OB2 =10,
即菱形的边长是10,
故答案为:10.
分析:根据菱形的性质求出OA和OB的长,再利用勾股定理进行计算求解即可。
14.3 3
考点:菱形的性质,轴对称﹣最短路线问题
解:如图作DH⊥AC垂足为H与AG交于点E,
∵四边形ABCD是菱形,
∵AB=AD=CD=BC=6,
∵∠B=60°,
∴∠ADC=∠B=60°,
∴△ADC是等边三角形,
∵AG是中线,
∴∠GAD=∠GAC
∴点H关于AG的对称点F在AD上,此时EF+ED最小=DH.
在RT△DHC中,∵∠DHC=90°,DC=6,∠CDH= 12 ∠ADC=30°,
∴CH= 12 DC=3,DH= CD2-CH2 = 62-32 =3 3 ,
∴EF+DE的最小值=DH=3 3
故答案为3 3 .
分析:作DH⊥AC垂足为H与AG交于点E,点H关于AG的对称点为F,此时EF+ED最小=DH,先证明△ADC是等边三角形,在RT△DCH中利用勾股定理即可解决问题.
15. 9.6
考点:菱形的性质
解:连接AC、OA,如图所示,
∵四边形ABCD为菱形,对角线 BD=16 ,边长为10,
∴DG=8,AC⊥BD,
∴AG= 102-82=6 ,
∵ SΔABD=SΔBOA+SΔDOA ,
即 12BD·AG=12AB·OE+12AD·OF ,
∴ 16×6=10OE+10OF ,
解得:OE+OF=9.6,
故答案为:9.6.
分析:连接AC、OA,先由菱形性质得到DG=8,AC⊥BD,再由勾股定理得到AG=6,接着根据SΔABD=SΔBOA+SΔDOA , 由等面积法得到OE+OF的值.
三、解答题
16. 解:∵AC⊥BD,∴△AOB、△BOC为直角三角形,
∵E、F分别是AB、BC的中点,
∴OE= 12AB ,OF= 12BC ,
∵AB=BC,
∴OE=OF.
考点:菱形的性质
分析:根据菱形ABCD,可得AC⊥BD,所以可得△AOB、△BOC为直角三角形,再利用直角三角形斜边的中线等于斜边的一半即可证明OE=OF.
17. 证明:∵四边形ABCD是菱形,
∴AB=AD,∠B=∠D,
∵BE=DF
∴△ABE≌△ADF.
∴AE=CF
考点:菱形的性质
分析:由菱形性质得AB=AD,∠B=∠D,根据全等三角形判定SAS可得△ABE≌△ADF,由全等三角形性质即可得证.
18. (1)证明:因为四边形ABCD是菱形,
所以 AC⊥BD ,
∴∠COD=90° ,
∵CE//OD,DE//OC ,
所以四边形OCED是平行四边形,
∵∠COD=90° ,
∴四边形OCED是矩形;
(2)解:由(1)知,四边形OCED是矩形,
则CE=OD=1,
∵四边形ABCD是菱形,
∴AB=AD=CD=BC,
∵菱形ABCD的周长为 45 ,
∴CD=5 ,
∴OC=CD2-OD2=2 ,
∵AC=2OC=4,BD=2OD=2 ,
∴菱形ABCD的面积为: 12AC?BD=12×4×2=4 .
考点:菱形的性质,矩形的判定与性质
分析:(1)欲证明四边形OCED是矩形,只需推知四边形OCED是平行四边形,且有一内角为90度即可;
(2)由菱形的对角线互相垂直平分和菱形的面积公式解答.
19. (1)证明:在菱形ABCD中
OC= 12 AC,AC⊥BD,
∵DE= 12 AC,
∴DE=OC,
∵DE∥OC,
∴四边形OCED是平行四边形,
∵AC⊥BD,
∴□OCED是矩形,
∴OE=CD.
(2)解:在菱形ABCD中,AB=BC=4,
∵∠ABC=60?,
∴△ABC是等边三角形,
∴AC=AB=4,OA= 12 AC=2,
在Rt△AOB中, OB=AB2-OA2=23 ,
∵四边形OCED是矩形,
∴OD=CE=OB= 23 ,
在Rt△ACE中, AE=AC2+CE2=27 .
考点:等边三角形的判定与性质,勾股定理,平行四边形的判定,菱形的性质,矩形的判定与性质
分析:(1)先求出四边形OCED是平行四边形,再根据菱形的对角线互相垂直求出∠COD=90°,证明OCED是矩形,可得OE=CD即可;(2)根据菱形的性质得出AC=AB,再根据勾股定理得出AE的长度即可.
一、单选题
1.下面性质中,菱形不一定具备的是(?? )
A.?四条边都相等???????????????B.?每一条对角线平分一组对角???????????????C.?邻角互补???????????????D.?对角线相等
2.如图,在菱形ABCD中,对角线AC, BD相交于点O.下列结论不一定成立的是 (??? )
A.?BD平分∠ADC??????????????????????????B.?AC=BD??????????????????????????C.?AC⊥BD??????????????????????????D.?OA=OC
3.下列性质中,菱形对角线不具有的是(?? )
A.?对角线互相垂直???????????B.?对角线所在直线是对称轴???????????C.?对角线相等???????????D.?对角线互相平分
4.已知菱形 ABCD 中,对角线 AC 与 BD 交于点O, BD=10 , AC=24 ,则该菱形的周长是(?? )
A.?13???????????????????????????????????????B.?52???????????????????????????????????????C.?120???????????????????????????????????????D.?240
5.若菱形的两条对角线长分别为8和6,则这个菱形的面积是(?? )
A.?96?????????????????????????????????????????B.?48?????????????????????????????????????????C.?24?????????????????????????????????????????D.?12
6.菱形 ABCD 的边长是 5cm ,一条对角线 AC 的长是 8cm ,则此菱形的面积为(?? )
A.?40cm2??????????????????????????????B.?48cm2??????????????????????????????C.?243cm2??????????????????????????????D.?24cm2
7.如图,菱形 ABCD 中, ∠A=50° ,则 ∠ADB 的度数为(?? )
A.?65°????????????????????????????????????B.?55°????????????????????????????????????C.?45°????????????????????????????????????D.?25°
8.菱形的一个内角是 60° ,边长是 3cm ,则这个菱形的较短的对角线长是(???? )
A.?32cm????????????????????????????????B.?323cm????????????????????????????????C.?3cm????????????????????????????????D.?33cm
9.数轴上两点A、C表示的数分别为-2,6,以 AC 为对角线做菱形 ABCD ,连接 BD 交 AC 于O点,则O点所表示的数为( )
A.?-1??????????????????????????????????????????B.?1??????????????????????????????????????????C.?2??????????????????????????????????????????D.?3
10.菱形的两条对角线把菱形分成全等的直角三角形的个数是( )
A.?1个???????????????????????????????????????B.?2个???????????????????????????????????????C.?3个???????????????????????????????????????D.?4个
二、填空题
11.一个菱形的边长是 5cm ,一条对角线长 6cm ,则此菱形的面积为________ cm2 .
12.若菱形的面积为24,一条对角线长为8,则另一条对角线长为________,边长为________.
13.菱形的两条对角线分别是12和16,则此菱形的边长是________.
14.如图,在菱形ABCD中,AB=6,∠B=60°,点G是边CD边的中点,点E、F分别是AG、AD上的两个动点,则EF+ED的最小值是________.
15.如图,在边长为10的菱形 ABCD 中,对角线 BD=16 ,点O是线段 BD 上的动点, OE⊥AB 于E, OF⊥AD 于F.则 OE+OF= ________.
三、解答题
16.在如图菱形ABCD中,对角线AC、BD相交于O,E、F分别是AB、BC的中点.求证:OE=OF.
17.已知:如图,在菱形ABCD中,点E,F分别在边BC,CD上,且BE=DF,连结AE,AF.求证:AE=AF.
18.如图,在菱形ABCD,对角线AC,与BD交于点O,过点C作BD的平行线,过点D作AC的平行线,两直线交于点E,
(1)求证:四边形OCED是矩形;
(2)若CE=1,菱形ABCD的周长为 45 ,求菱形ABCD的面积.
19.如图,菱形ABCD的对角线AC,BD相交于点O,过点D作 DE//AC ,且 DE=12AC ,连接 CE,OE ,连接 AE 交 OD 于点F.
(1)求证: OE=CD ;
(2)若菱形ABCD的边长为4, ∠ABC=60? ,求 AE 的长.
答案解析部分
一、单选题
1. D
考点:菱形的性质
解:A. 菱形的四条边都相等,说法正确,不符合题意;
B. 菱形的每一条对角线平分一组对角,说法正确,不符合题意;
C. 菱形的邻角互补,说法正确,不符合题意;
D. 菱形的对角线不一定相等,说法不正确,符合题意.
故答案为:D.
分析:根据菱形的性质即可得出答案.
2. B
考点:菱形的性质
解:∵四边形ABCD是菱形,
∴BD平分∠ADC,OA=OC,AC⊥BD,
无法得出AC=BD,
B符合题意,选项A、C、D不符合题意,
故答案为:B.
分析:利用菱形的性质邻边相等、对角线互相垂直且平分进而分析即可.
3.C
考点:菱形的性质
解:∵菱形对角线具有的性质有:对角线互相垂直,对角线互相平分, ∴对角线所在直线是对称轴.
故A,B,D正确,C错误.
故选C.
分析:由菱形的对角线互相平分且垂直,可得菱形对角线所在直线是对称轴,继而求得答案.
4. B
考点:菱形的性质
解:∵菱形ABCD中,BD=10,AC=24,
∴OB=5,OA=12,∠AOB=90°
在Rt△ABO中,AB= 52+122 =13,
∴菱形ABCD的周长=4AB=52.
故答案为:B.
分析:由菱形的对角线垂直且互相平分得出OB=5,OA=12,∠AOB=90°,从而利用勾股定理算出AB的长,继而求得菱形ABCD的周长.
5. C
考点:菱形的性质
解:∵四边形ABCD是菱形,
∴S= 12 ×6×8=24.
故答案为:C.
分析:根据菱形的面积等于对角线乘积的一半计算即可.
6. D
考点:菱形的性质
解:根据题意画出图形,如图所示:
∵ 四边形 ABCD 是菱形,
∴AB=BC=CD=AD=5cm , AC⊥BD , OA=OC , OB=OD ,
又 AC 的长是 8cm ,
∴OA=4cm ,
∴OB=AB2-OA2=52-42=3cm ,
∴BD=6cm ,
∴ 菱形的面积 =12AC·BD=12×8×6=24cm2 .
故答案为:D.
分析:根据菱形 ABCD 的边长是 5cm ,一条对角线 AC 的长是 8cm ,可以求出另一条对角线的长度是 6cm ,利用菱形的面积等于 12AC·BD 可求出结果.
7. A
考点:菱形的性质
解:∵四边形ABCD为菱形,∴AD=AB,
∴∠ADB=∠ABD=(180°-∠A)÷2=(180°-50°)÷2=65°,
故答案为:A.
分析:由菱形的性质可得AD=AB,于是根据等边对等角可得∠ADB=∠ABD,然后由三角形内角和定理可求解.
8. C
考点:菱形的性质
解:因为菱形的四边相等,当一个内角是60°,则较短对角线与两边组成等边三角形.
∵菱形的边长是 3cm ,
∴这个菱形的较短的对角线长是3cm.
故答案为:C.
分析:根据 菱形的一个内角是?60°? , 边长是?3cm ,进行求解即可。
9. C
考点:菱形的性质
解:AC=6-(-2)=8
以 AC 为对角线做菱形 ABCD ,连接 BD 交 AC 于O点,
AO=CO=4,
O点表示数为:-2+4=2,
故答案为:C.
分析:先确定AC的长,然后由菱形的性质,对角线互相平分求出AO的长,利用A点坐标加AO即可.
10. D
考点:菱形的性质
解:如图所示:
∵AC,BD是菱形的对角线,
∴AC⊥BD,且DE=BE,AE=CE,
∵AD=CD=BC=AB,
∴在Rt△ADE和Rt△ABE中, {AD=ABAE=AE ,
∴Rt△ADE≌Rt△ABE(HL),
同理可得出Rt△ADE≌Rt△CDE,Rt△CDE≌Rt△CBE,Rt△ABE≌Rt△CBE.
∴Rt△ADE≌Rt△CDE≌Rt△ABE≌Rt△CBE,
∴菱形中两条对角线把菱形分成全等中直角三角形的个数是4个,
故答案为:D.
分析:利用菱形的性质得出对角线垂直且互相平分,且4条边相等,即可得到全等的直角三角形的个数是4个.
二、填空题
11. 24
考点:菱形的性质
解:如图, AB=5cm,AC=6cm ,
∵四边形ABCD是菱形,
∴ AO=12AC=3cm,OB=12BD,AC⊥BD ,
∴∠AOB=90° ?,
∴BO=AB2-AO2=4cm ,
∴BD=2OB=8cm ,
∴S=12AC?BD=12×6×8=24cm2 ,
故答案为:24.
分析:首先根据菱形的性质和勾股定理求出另一条对角线的长度,然后利用菱形的面积公式求解即可.
12. 6;5
考点:菱形的性质
解:如图:
∵菱形ABCD的面积为24
∴ 12 AC·BD=24,
∵AC=8,
∴BD=6;
∵四边形ABCD是菱形,
∴AB=BC=CD=DA,AC⊥BD,
∴OA= 12 AC=4,OB= 12 BD=3,
∴AB= OA2+OB2=32+42 =5.
故答案为6,5.
分析:根菱形面积等于对角线积的一半,即可求得另一条对角线的长度,然后根据勾股定理即可求得菱形的边长.
13. 10
考点:菱形的性质
解:如图,
∵菱形ABCD中,AC=12,BD=16,
∴OA= 12 AC=6,OB= 12 BD=8,AC⊥BD,
∴AB= OA2+OB2 =10,
即菱形的边长是10,
故答案为:10.
分析:根据菱形的性质求出OA和OB的长,再利用勾股定理进行计算求解即可。
14.3 3
考点:菱形的性质,轴对称﹣最短路线问题
解:如图作DH⊥AC垂足为H与AG交于点E,
∵四边形ABCD是菱形,
∵AB=AD=CD=BC=6,
∵∠B=60°,
∴∠ADC=∠B=60°,
∴△ADC是等边三角形,
∵AG是中线,
∴∠GAD=∠GAC
∴点H关于AG的对称点F在AD上,此时EF+ED最小=DH.
在RT△DHC中,∵∠DHC=90°,DC=6,∠CDH= 12 ∠ADC=30°,
∴CH= 12 DC=3,DH= CD2-CH2 = 62-32 =3 3 ,
∴EF+DE的最小值=DH=3 3
故答案为3 3 .
分析:作DH⊥AC垂足为H与AG交于点E,点H关于AG的对称点为F,此时EF+ED最小=DH,先证明△ADC是等边三角形,在RT△DCH中利用勾股定理即可解决问题.
15. 9.6
考点:菱形的性质
解:连接AC、OA,如图所示,
∵四边形ABCD为菱形,对角线 BD=16 ,边长为10,
∴DG=8,AC⊥BD,
∴AG= 102-82=6 ,
∵ SΔABD=SΔBOA+SΔDOA ,
即 12BD·AG=12AB·OE+12AD·OF ,
∴ 16×6=10OE+10OF ,
解得:OE+OF=9.6,
故答案为:9.6.
分析:连接AC、OA,先由菱形性质得到DG=8,AC⊥BD,再由勾股定理得到AG=6,接着根据SΔABD=SΔBOA+SΔDOA , 由等面积法得到OE+OF的值.
三、解答题
16. 解:∵AC⊥BD,∴△AOB、△BOC为直角三角形,
∵E、F分别是AB、BC的中点,
∴OE= 12AB ,OF= 12BC ,
∵AB=BC,
∴OE=OF.
考点:菱形的性质
分析:根据菱形ABCD,可得AC⊥BD,所以可得△AOB、△BOC为直角三角形,再利用直角三角形斜边的中线等于斜边的一半即可证明OE=OF.
17. 证明:∵四边形ABCD是菱形,
∴AB=AD,∠B=∠D,
∵BE=DF
∴△ABE≌△ADF.
∴AE=CF
考点:菱形的性质
分析:由菱形性质得AB=AD,∠B=∠D,根据全等三角形判定SAS可得△ABE≌△ADF,由全等三角形性质即可得证.
18. (1)证明:因为四边形ABCD是菱形,
所以 AC⊥BD ,
∴∠COD=90° ,
∵CE//OD,DE//OC ,
所以四边形OCED是平行四边形,
∵∠COD=90° ,
∴四边形OCED是矩形;
(2)解:由(1)知,四边形OCED是矩形,
则CE=OD=1,
∵四边形ABCD是菱形,
∴AB=AD=CD=BC,
∵菱形ABCD的周长为 45 ,
∴CD=5 ,
∴OC=CD2-OD2=2 ,
∵AC=2OC=4,BD=2OD=2 ,
∴菱形ABCD的面积为: 12AC?BD=12×4×2=4 .
考点:菱形的性质,矩形的判定与性质
分析:(1)欲证明四边形OCED是矩形,只需推知四边形OCED是平行四边形,且有一内角为90度即可;
(2)由菱形的对角线互相垂直平分和菱形的面积公式解答.
19. (1)证明:在菱形ABCD中
OC= 12 AC,AC⊥BD,
∵DE= 12 AC,
∴DE=OC,
∵DE∥OC,
∴四边形OCED是平行四边形,
∵AC⊥BD,
∴□OCED是矩形,
∴OE=CD.
(2)解:在菱形ABCD中,AB=BC=4,
∵∠ABC=60?,
∴△ABC是等边三角形,
∴AC=AB=4,OA= 12 AC=2,
在Rt△AOB中, OB=AB2-OA2=23 ,
∵四边形OCED是矩形,
∴OD=CE=OB= 23 ,
在Rt△ACE中, AE=AC2+CE2=27 .
考点:等边三角形的判定与性质,勾股定理,平行四边形的判定,菱形的性质,矩形的判定与性质
分析:(1)先求出四边形OCED是平行四边形,再根据菱形的对角线互相垂直求出∠COD=90°,证明OCED是矩形,可得OE=CD即可;(2)根据菱形的性质得出AC=AB,再根据勾股定理得出AE的长度即可.
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
