6.2.1 反比例函数的图象同步练习(含解析)
文档属性
| 名称 | 6.2.1 反比例函数的图象同步练习(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1008.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-11 17:56:19 | ||
图片预览




文档简介
初中数学浙教版八年级下册6.2.1反比例函数的图象 同步练习
一、单选题
1.若反比例函数的图象经过点(﹣1,4),则它的函数表达式是(?? )
A.?y =-4x????????????????????????????B.?y =-14x????????????????????????????C.?y =4x????????????????????????????D.?y =14x
2.下列各点中,在反比例函数 y=4x 图象上的点是(?? )
A.?(-1,4)???????????????????????????????B.?(1,4)???????????????????????????????C.?(-2,2)???????????????????????????????D.?(2,-2)
3.已知反比例函数 y=k-5x 的图象分别位于一、三象限,则k的取值范围是(? )
A.?k>5????????????????????????????????????B.?k<5????????????????????????????????????C.?k>-5????????????????????????????????????D.?k<-5
4.当 x>0 时,函数 y=-5x 的图象在(??? )
A.?第四象限???????????????????????????B.?第三象限???????????????????????????C.?第二象限???????????????????????????D.?第一象限
5.若反比例函数 y=kx 的图象经过点 (-1,-2) ,则该反比例函数的图象位于(?? )
A.?第一、二象限??????????????????B.?第二、三象限??????????????????C.?第二、四象限??????????????????D.?第一、三象限
6.在平面直角坐标系中,点 A(1,2) 在双曲线 y=k1x 上,点A关于x轴的对称点B在双曲线 y=k2x 上,则 k1+k2 的值是(?? )
A.?2??????????????????????????????????????????B.?1??????????????????????????????????????????C.?0??????????????????????????????????????????D.?-1
7.若反比例函数 y=2a-1x 的图象在第二,四象限,则m的值是( ??)
A.?a > 12???????????????????????????????B.?a < 12???????????????????????????????C.?a > 2???????????????????????????????D.?a < 2
8.在同一直角坐标系中,函数y=kx﹣k与y= kx (k≠0)的图象大致是(??? )
A.?????????B.?????????C.?????????D.?
9.一次函数y=ax+b与反比例函数 y=cx 的图象如图所示,则(?? )
A.?a>0,b>0,c>0???????B.?a<0,b<0,c<0???????C.?a<0,b>0,c>0???????D.?a<0,b<0,c>0
10.如图,函数 y={1x(x>0)-1x(x<0) 的图象所在坐标系的原点是(?? )
A.?点 M???????????????????????????????????B.?点 N???????????????????????????????????C.?点 P???????????????????????????????????D.?点 Q
二、填空题
11.写出一个图象经过二、四象限的反比例函数的表达式________.(只需写出一个正确的函数表达式即可)
12.如果反比例函数y= k-3x 的图象位于第二、四象限,那么满足条件的正整数k的值是________.
13.反比例函数图像经过点(2,-3),则它的函数表达式是________.
14.若点A(1,-2)、B(-2,a)在同一个反比例函数的图象上,则a的值为________.
三、解答题
15.已知正比例函数 y=-3x 与反比例函数交于A(-2,a),求这个反比例函数的解析式。
16.启航同学根据学习函数的经验,对函数 y=1|-x+1| 的图象与性质进行了探究.下面是他的探究过程,请补充完成:
(1)函数 y=1|-x+1| 的自变量x 的取值范围是________;
(2)列表,找出y 与x 的几组对应值,列表如下:
x
…
-2
-1
0
12
32
2
3
..
y
…
a
12
1
2
2
1
12
…
其中, a=________;
(3)在平面直角坐标系xOy 中,描出以上表中各对对 应值为坐标的点,并画出该函数的图象并写出该函数的一条性质:
17.有这样一个问题:探究函数 y=x+2x 的图象与性质.小美根据学习函数的经验,对函数 y=x+2x 的图象与性质进行了探究.下面是小美的探究过程,请补充完整:
(1)函数 y=x+2x 的自变量x的取值范围是________
(2)下表是y与x的几组对应值.m的值为________
x
-2
-32
-1
-12
13
12
1
2
3
4
…
y
0
-23
-1
-6
21
10
3
m
53
64
…
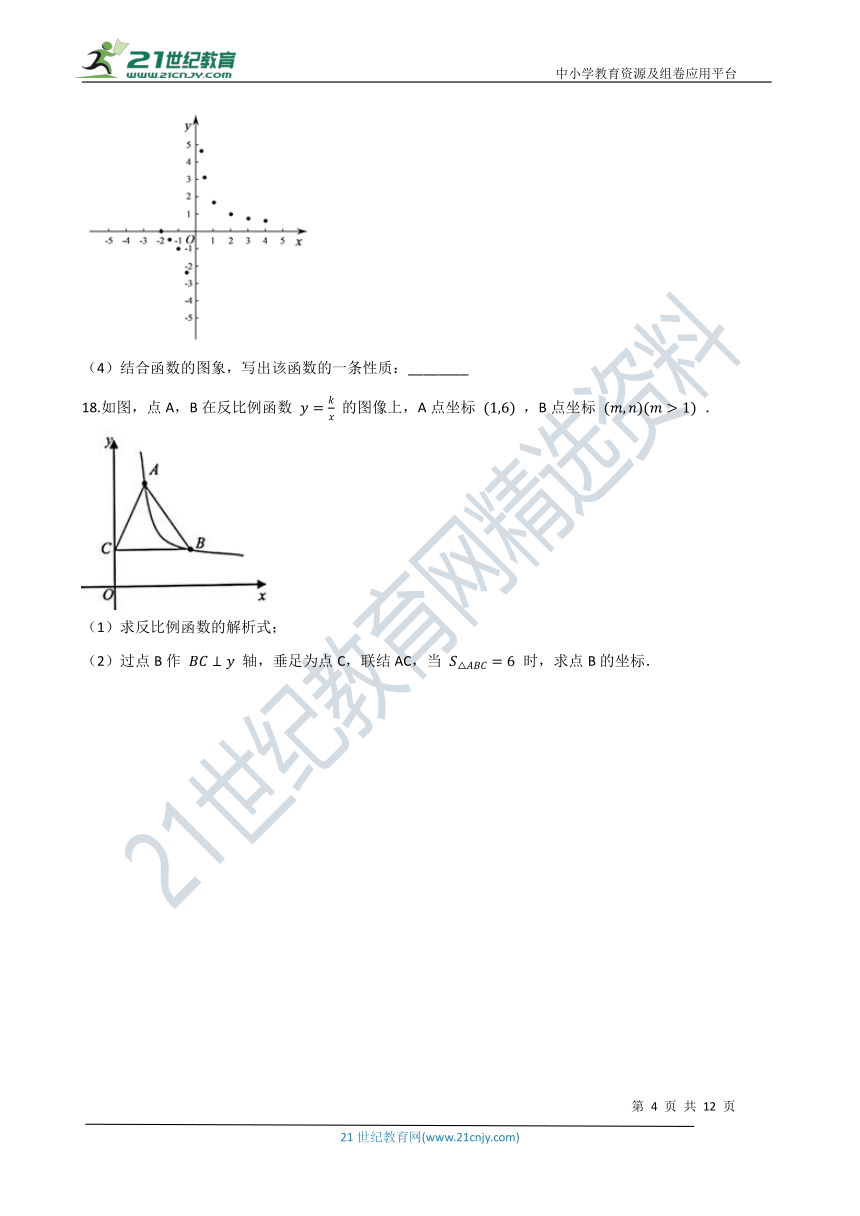
(3)如下图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;
(4)结合函数的图象,写出该函数的一条性质:________
18.如图,点A,B在反比例函数 y=kx 的图像上,A点坐标 (1,6) ,B点坐标 (m,n)(m>1) .
(1)求反比例函数的解析式;
(2)过点B作 BC⊥y 轴,垂足为点C,联结AC,当 S△ABC=6 时,求点B的坐标.
答案解析部分
一、单选题
1. A
考点:待定系数法求反比例函数解析式
解:∵反比例函数的图象经过点(﹣1,4),
∴ k=(-1)×4=-4 ,
∴反比例函数的关系式是y =-4x .
故答案为:A.
分析:先根据反比例函数中 k=xy 的特点求出 k 的值,即可得出结论.
2. B
考点:反比例函数图象上点的坐标特征
解: ∵y=4x ,
∴xy=4 ,
A、 ∵-1×4=-4≠4 ,
∴ 点 (-1,4) 不在反比例函数 y=4x 图象上,故本选项不合题意;
B、 ∵1×4=4=4 ,
∴ 点 (1,4) 在反比例函数 y=4x 图象上,故本选项符合题意;
C、 ∵-2×2=-4≠4 ,
∴ 点 (-2,2) 不在反比例函数 y=4x 图象上,故本选项不合题意;
D、 ∵-2×2=-4≠4 ,
∴ 点 (2,-2) 不在反比例函数 y=4x 图象上,故本选项不合题意.
故答案为:B.
分析:根据反比例函数解析式可得 xy=4 ,然后对各选项分析判断即可得解.
3. A
考点:反比例函数的性质
解:∵反比例函数 y=k-5x 图象的两个分支分别位于第一、三象限,
∴ k-5>0 ,解得 k>5 .
故答案为:A.
分析:由题意根据反比例函数的图象与系数的关系列出关于k的不等式,求出k的取值范围即可.
4. A
考点:反比例函数的性质
解:∵反比例函数 y=-5x 的系数 -5<0 ,∴图象两个分支分别位于第二、四象限.
∴当 x>0 时,图象位于第四象限.故答案为:A.
分析:根据反比例函数 y=kx(k≠0) 的性质:当 k>0 时,图象分别位于第一、三象限;当 k<0 时,图象分别位于第二、四象限.
5. D
考点:反比例函数的图象
解:∵ 反比例函数图象经过点 (-1,-2) ,
∴ -2=k-1
∴ k=2
∴该反比例函数图像位于第一、三象限,
故答案为D.
分析:首先将点坐标代入函数解析式,即可得出 k 的值,即可判定反比例函数所处的象限.
6. C
考点:待定系数法求反比例函数解析式,关于坐标轴对称的点的坐标特征
解: ∵ 点 A(1,2) 在双曲线 y=k1x 上,
∴k1=1×2=2 ;
又 ∵ 点A与点B关于x轴的对称,
∴B(1,-2)
∵ 点B在双曲线 y=k2x 上,
∴k2=1×(-2)=-2 ;
∴k1+k2=2-2=0 ;
故答案为:C.
分析:由点 A(1,2) 在双曲线 y=k1x 上,可得 k1=2 ,由点A与点B关于x轴的对称,可得到点B的坐标,进而表示出 k2 ,然后得出答案.
7. B
考点:反比例函数的性质
解:∵反比例函数 y=2a-1x 的图象在第二、四象限,
∴2a?1<0,
解得:a < 12 .
故答案为:B.
分析:直接利用反比例函数的性质得出关于a的不等式进而得出答案.
8. B
考点:反比例函数的图象,一次函数图象、性质与系数的关系
解:①当k>0时,
一次函数y=kx﹣k经过一、三、四象限,
反比例函数的 y=kx(k≠0) 的图象经过一、三象限,
故B选项的图象符合要求,
②当k<0时,
一次函数y=kx﹣k经过一、二、四象限,
反比例函数的 y=kx(k≠0) 的图象经过二、四象限,
没有符合条件的选项.
故答案为:B.
分析:根据k的取值范围,分别讨论k>0和k<0时的情况,然后根据一次函数和反比例函数图象的特点进行选择符合题意答案.
9. A
考点:反比例函数的性质,一次函数图象、性质与系数的关系
解:根据反比例函数 y=cx 的图象,判断 c>0 , 根据一次函令x=0,则 y=b>0 , 数y=ax+b的图象知 a>0 , 故 a>0,b>0,c>0,
?故答案为:.A
分析:根据反比例函数 y=cx 的图象,可判断 c ,根据一次函数y=ax+b的图象判断 a,b ,故可得出答案.
10. A
考点:反比例函数的图象,反比例函数的性质
解:由已知可知函数y ={1x(x>0),-1x(x<0) 关于y轴对称,∴y轴与直线PM重合.当x>0时,图象在一象限,当x<0时,图象在二象限,即图象在x轴上方,所以点M是原点.
故答案为:A.
分析:由函数解析式可知函数关于y轴对称,当x>0时,图象在一象限,当x<0时,图象在二象限,即可求解.
二、填空题
11. y=? 1x (答案不唯一)
考点:反比例函数的图象
解:根据反比例函数的性质,其图象位于第二、四象限,则其系数k<0;
故只要给出k小于0的反比例函数即可;答案不唯一,如y=? 1x 等.
故答案为:y=? 1x (答案不唯一).
分析:根据反比例函数的系数与图象所过象限的关系,易得答案.
12. 1,2
考点:反比例函数的图象
解:本题考查的是反比例函数的图象的性质
由反比例函数的性质列出不等式,解出k的范围,在这个范围写出k的整数解则可.
由题意得k-3<0,k<3,则满足该条件的正整数k的值是1,2.
分析:根据反比例函数图象在第二、四象限可以得到k-3<0,再求解即可。
13. y=-6x
考点:待定系数法求反比例函数解析式
解:设反比例函数的解析式是 y=kx .则 -3=k2 ,得 k=-6 ,则这个函数的表达式是 y=-6x .故答案为 y=-6x .
分析:利用待定系数法求反比例函数解析式即可。
14. 1
考点:反比例函数图象上点的坐标特征
解:∵点A(1,-2)、B(-2,a)在同一反比例函数的图象上,
∴1×(-2)=-2a,
解得:a=1.
故答案为:1.
分析:由A、B点的坐标结合反比例函数图象上点的坐标特征即可得出关于a的一元一次方程,解方程即可得出结论.
三、解答题
15. 解:将点A(-2,a)代入 y=-3x 中,解得: a=6
故点A的坐标为:(-2,6)
设反比例函数的解析式为: y=kx (k≠0)
将点A的坐标代入得:
6=k-2
解得: k=-12
∴这个反比例函数的解析式为: y=-12x .
考点:待定系数法求反比例函数解析式
分析:将点A坐标代入正比例函数的解析式中,即可求出点A的坐标,然后设出反比例函数的解析式,将点A坐标代入反比例函数解析式中,即可求出反比例函数的解析式.
16. (1)x≠1
(2)13
(3)解: ;函数图像经过第一、二象限(答案不唯一)
考点:函数自变量的取值范围,反比例函数的图象
解:(1)在函数 y=1|-x+1| 中,
|-x+1|≠0 ,
解得:x≠1,
∴自变量x 的取值范围是x≠1,
故答案为:x≠1;
(2)∵当x=-2时,a= 1|2+1| = 13 ,
故答案为: 13 ;
分析:(1)根据分式有意义的条件即可得出结论;
(2)把x=-2代入函数解析式,求出y的值即可;
(3)在坐标系内描出各点,再顺次连接即可得到图像,再根据函数图象即可得性质.
17. (1)x≥-2且x≠0
(2)m=1
(3)解:如图所示;
(4)若x>0,y随x的增大而减小
考点:函数自变量的取值范围,反比例函数的图象
分析:(1)根据被开方数非负以及分母不为0即可得出关于x的一元一次不等式组,解之即可得出结论;(2)将x=2代入函数解析式中求出m值即可;(3)在坐标系中描出上述点的坐标,连点成线即可画出函数图象;(4)观察函数图象,根据函数图象可寻找到函数值随自变量的变化规律.
18. (1)解:把点A(1,6)代入反比例函数 y=kx 中得:
6=k1 ,
∴ k=6 ,
∴反比例函数解析式为: y=6x ;
(2)解:∵ S△ABC=6 ,
∴ 12m(6-n)=6 ,
∵反比例函数 y=kx(x>0) 的图像经过点 B(m,n)(m>1) ;
∴ n=6m ,
∴ 12m(6-6m)=6 ,
解得: m=3 ,
∴ n=63=2 ,
∴B点坐标为 (3,2) .
考点:待定系数法求反比例函数解析式,三角形的面积
分析:(1)根据待定系数法求解即可;
(2)根据三角形面积得到关于m的方程,解方程求解即可。
一、单选题
1.若反比例函数的图象经过点(﹣1,4),则它的函数表达式是(?? )
A.?y =-4x????????????????????????????B.?y =-14x????????????????????????????C.?y =4x????????????????????????????D.?y =14x
2.下列各点中,在反比例函数 y=4x 图象上的点是(?? )
A.?(-1,4)???????????????????????????????B.?(1,4)???????????????????????????????C.?(-2,2)???????????????????????????????D.?(2,-2)
3.已知反比例函数 y=k-5x 的图象分别位于一、三象限,则k的取值范围是(? )
A.?k>5????????????????????????????????????B.?k<5????????????????????????????????????C.?k>-5????????????????????????????????????D.?k<-5
4.当 x>0 时,函数 y=-5x 的图象在(??? )
A.?第四象限???????????????????????????B.?第三象限???????????????????????????C.?第二象限???????????????????????????D.?第一象限
5.若反比例函数 y=kx 的图象经过点 (-1,-2) ,则该反比例函数的图象位于(?? )
A.?第一、二象限??????????????????B.?第二、三象限??????????????????C.?第二、四象限??????????????????D.?第一、三象限
6.在平面直角坐标系中,点 A(1,2) 在双曲线 y=k1x 上,点A关于x轴的对称点B在双曲线 y=k2x 上,则 k1+k2 的值是(?? )
A.?2??????????????????????????????????????????B.?1??????????????????????????????????????????C.?0??????????????????????????????????????????D.?-1
7.若反比例函数 y=2a-1x 的图象在第二,四象限,则m的值是( ??)
A.?a > 12???????????????????????????????B.?a < 12???????????????????????????????C.?a > 2???????????????????????????????D.?a < 2
8.在同一直角坐标系中,函数y=kx﹣k与y= kx (k≠0)的图象大致是(??? )
A.?????????B.?????????C.?????????D.?
9.一次函数y=ax+b与反比例函数 y=cx 的图象如图所示,则(?? )
A.?a>0,b>0,c>0???????B.?a<0,b<0,c<0???????C.?a<0,b>0,c>0???????D.?a<0,b<0,c>0
10.如图,函数 y={1x(x>0)-1x(x<0) 的图象所在坐标系的原点是(?? )
A.?点 M???????????????????????????????????B.?点 N???????????????????????????????????C.?点 P???????????????????????????????????D.?点 Q
二、填空题
11.写出一个图象经过二、四象限的反比例函数的表达式________.(只需写出一个正确的函数表达式即可)
12.如果反比例函数y= k-3x 的图象位于第二、四象限,那么满足条件的正整数k的值是________.
13.反比例函数图像经过点(2,-3),则它的函数表达式是________.
14.若点A(1,-2)、B(-2,a)在同一个反比例函数的图象上,则a的值为________.
三、解答题
15.已知正比例函数 y=-3x 与反比例函数交于A(-2,a),求这个反比例函数的解析式。
16.启航同学根据学习函数的经验,对函数 y=1|-x+1| 的图象与性质进行了探究.下面是他的探究过程,请补充完成:
(1)函数 y=1|-x+1| 的自变量x 的取值范围是________;
(2)列表,找出y 与x 的几组对应值,列表如下:
x
…
-2
-1
0
12
32
2
3
..
y
…
a
12
1
2
2
1
12
…
其中, a=________;
(3)在平面直角坐标系xOy 中,描出以上表中各对对 应值为坐标的点,并画出该函数的图象并写出该函数的一条性质:
17.有这样一个问题:探究函数 y=x+2x 的图象与性质.小美根据学习函数的经验,对函数 y=x+2x 的图象与性质进行了探究.下面是小美的探究过程,请补充完整:
(1)函数 y=x+2x 的自变量x的取值范围是________
(2)下表是y与x的几组对应值.m的值为________
x
-2
-32
-1
-12
13
12
1
2
3
4
…
y
0
-23
-1
-6
21
10
3
m
53
64
…
(3)如下图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;
(4)结合函数的图象,写出该函数的一条性质:________
18.如图,点A,B在反比例函数 y=kx 的图像上,A点坐标 (1,6) ,B点坐标 (m,n)(m>1) .
(1)求反比例函数的解析式;
(2)过点B作 BC⊥y 轴,垂足为点C,联结AC,当 S△ABC=6 时,求点B的坐标.
答案解析部分
一、单选题
1. A
考点:待定系数法求反比例函数解析式
解:∵反比例函数的图象经过点(﹣1,4),
∴ k=(-1)×4=-4 ,
∴反比例函数的关系式是y =-4x .
故答案为:A.
分析:先根据反比例函数中 k=xy 的特点求出 k 的值,即可得出结论.
2. B
考点:反比例函数图象上点的坐标特征
解: ∵y=4x ,
∴xy=4 ,
A、 ∵-1×4=-4≠4 ,
∴ 点 (-1,4) 不在反比例函数 y=4x 图象上,故本选项不合题意;
B、 ∵1×4=4=4 ,
∴ 点 (1,4) 在反比例函数 y=4x 图象上,故本选项符合题意;
C、 ∵-2×2=-4≠4 ,
∴ 点 (-2,2) 不在反比例函数 y=4x 图象上,故本选项不合题意;
D、 ∵-2×2=-4≠4 ,
∴ 点 (2,-2) 不在反比例函数 y=4x 图象上,故本选项不合题意.
故答案为:B.
分析:根据反比例函数解析式可得 xy=4 ,然后对各选项分析判断即可得解.
3. A
考点:反比例函数的性质
解:∵反比例函数 y=k-5x 图象的两个分支分别位于第一、三象限,
∴ k-5>0 ,解得 k>5 .
故答案为:A.
分析:由题意根据反比例函数的图象与系数的关系列出关于k的不等式,求出k的取值范围即可.
4. A
考点:反比例函数的性质
解:∵反比例函数 y=-5x 的系数 -5<0 ,∴图象两个分支分别位于第二、四象限.
∴当 x>0 时,图象位于第四象限.故答案为:A.
分析:根据反比例函数 y=kx(k≠0) 的性质:当 k>0 时,图象分别位于第一、三象限;当 k<0 时,图象分别位于第二、四象限.
5. D
考点:反比例函数的图象
解:∵ 反比例函数图象经过点 (-1,-2) ,
∴ -2=k-1
∴ k=2
∴该反比例函数图像位于第一、三象限,
故答案为D.
分析:首先将点坐标代入函数解析式,即可得出 k 的值,即可判定反比例函数所处的象限.
6. C
考点:待定系数法求反比例函数解析式,关于坐标轴对称的点的坐标特征
解: ∵ 点 A(1,2) 在双曲线 y=k1x 上,
∴k1=1×2=2 ;
又 ∵ 点A与点B关于x轴的对称,
∴B(1,-2)
∵ 点B在双曲线 y=k2x 上,
∴k2=1×(-2)=-2 ;
∴k1+k2=2-2=0 ;
故答案为:C.
分析:由点 A(1,2) 在双曲线 y=k1x 上,可得 k1=2 ,由点A与点B关于x轴的对称,可得到点B的坐标,进而表示出 k2 ,然后得出答案.
7. B
考点:反比例函数的性质
解:∵反比例函数 y=2a-1x 的图象在第二、四象限,
∴2a?1<0,
解得:a < 12 .
故答案为:B.
分析:直接利用反比例函数的性质得出关于a的不等式进而得出答案.
8. B
考点:反比例函数的图象,一次函数图象、性质与系数的关系
解:①当k>0时,
一次函数y=kx﹣k经过一、三、四象限,
反比例函数的 y=kx(k≠0) 的图象经过一、三象限,
故B选项的图象符合要求,
②当k<0时,
一次函数y=kx﹣k经过一、二、四象限,
反比例函数的 y=kx(k≠0) 的图象经过二、四象限,
没有符合条件的选项.
故答案为:B.
分析:根据k的取值范围,分别讨论k>0和k<0时的情况,然后根据一次函数和反比例函数图象的特点进行选择符合题意答案.
9. A
考点:反比例函数的性质,一次函数图象、性质与系数的关系
解:根据反比例函数 y=cx 的图象,判断 c>0 , 根据一次函令x=0,则 y=b>0 , 数y=ax+b的图象知 a>0 , 故 a>0,b>0,c>0,
?故答案为:.A
分析:根据反比例函数 y=cx 的图象,可判断 c ,根据一次函数y=ax+b的图象判断 a,b ,故可得出答案.
10. A
考点:反比例函数的图象,反比例函数的性质
解:由已知可知函数y ={1x(x>0),-1x(x<0) 关于y轴对称,∴y轴与直线PM重合.当x>0时,图象在一象限,当x<0时,图象在二象限,即图象在x轴上方,所以点M是原点.
故答案为:A.
分析:由函数解析式可知函数关于y轴对称,当x>0时,图象在一象限,当x<0时,图象在二象限,即可求解.
二、填空题
11. y=? 1x (答案不唯一)
考点:反比例函数的图象
解:根据反比例函数的性质,其图象位于第二、四象限,则其系数k<0;
故只要给出k小于0的反比例函数即可;答案不唯一,如y=? 1x 等.
故答案为:y=? 1x (答案不唯一).
分析:根据反比例函数的系数与图象所过象限的关系,易得答案.
12. 1,2
考点:反比例函数的图象
解:本题考查的是反比例函数的图象的性质
由反比例函数的性质列出不等式,解出k的范围,在这个范围写出k的整数解则可.
由题意得k-3<0,k<3,则满足该条件的正整数k的值是1,2.
分析:根据反比例函数图象在第二、四象限可以得到k-3<0,再求解即可。
13. y=-6x
考点:待定系数法求反比例函数解析式
解:设反比例函数的解析式是 y=kx .则 -3=k2 ,得 k=-6 ,则这个函数的表达式是 y=-6x .故答案为 y=-6x .
分析:利用待定系数法求反比例函数解析式即可。
14. 1
考点:反比例函数图象上点的坐标特征
解:∵点A(1,-2)、B(-2,a)在同一反比例函数的图象上,
∴1×(-2)=-2a,
解得:a=1.
故答案为:1.
分析:由A、B点的坐标结合反比例函数图象上点的坐标特征即可得出关于a的一元一次方程,解方程即可得出结论.
三、解答题
15. 解:将点A(-2,a)代入 y=-3x 中,解得: a=6
故点A的坐标为:(-2,6)
设反比例函数的解析式为: y=kx (k≠0)
将点A的坐标代入得:
6=k-2
解得: k=-12
∴这个反比例函数的解析式为: y=-12x .
考点:待定系数法求反比例函数解析式
分析:将点A坐标代入正比例函数的解析式中,即可求出点A的坐标,然后设出反比例函数的解析式,将点A坐标代入反比例函数解析式中,即可求出反比例函数的解析式.
16. (1)x≠1
(2)13
(3)解: ;函数图像经过第一、二象限(答案不唯一)
考点:函数自变量的取值范围,反比例函数的图象
解:(1)在函数 y=1|-x+1| 中,
|-x+1|≠0 ,
解得:x≠1,
∴自变量x 的取值范围是x≠1,
故答案为:x≠1;
(2)∵当x=-2时,a= 1|2+1| = 13 ,
故答案为: 13 ;
分析:(1)根据分式有意义的条件即可得出结论;
(2)把x=-2代入函数解析式,求出y的值即可;
(3)在坐标系内描出各点,再顺次连接即可得到图像,再根据函数图象即可得性质.
17. (1)x≥-2且x≠0
(2)m=1
(3)解:如图所示;
(4)若x>0,y随x的增大而减小
考点:函数自变量的取值范围,反比例函数的图象
分析:(1)根据被开方数非负以及分母不为0即可得出关于x的一元一次不等式组,解之即可得出结论;(2)将x=2代入函数解析式中求出m值即可;(3)在坐标系中描出上述点的坐标,连点成线即可画出函数图象;(4)观察函数图象,根据函数图象可寻找到函数值随自变量的变化规律.
18. (1)解:把点A(1,6)代入反比例函数 y=kx 中得:
6=k1 ,
∴ k=6 ,
∴反比例函数解析式为: y=6x ;
(2)解:∵ S△ABC=6 ,
∴ 12m(6-n)=6 ,
∵反比例函数 y=kx(x>0) 的图像经过点 B(m,n)(m>1) ;
∴ n=6m ,
∴ 12m(6-6m)=6 ,
解得: m=3 ,
∴ n=63=2 ,
∴B点坐标为 (3,2) .
考点:待定系数法求反比例函数解析式,三角形的面积
分析:(1)根据待定系数法求解即可;
(2)根据三角形面积得到关于m的方程,解方程求解即可。
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
