第五章 特殊平行四边形章末检测题(基础篇含解析)
文档属性
| 名称 | 第五章 特殊平行四边形章末检测题(基础篇含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-11 18:01:28 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
初中数学浙教版八年级下册第五章 特殊平行四边形 章末检测(基础篇)
一、单选题(本大题共10小题,每小题3分,共30分。)
1.在四边形ABCD中,AB∥CD,AD∥BC,如果再添加一个条件,即可推出该四边形是菱形,这个条件可以是( )
A. BC=CD B. AB=CD C. ∠D=90° D. AD=BC
2.菱形具有而矩形不具有的性质是( )
A. 两组对边分别平行 B. 对角线互相垂直 C. 对角线互相平分 D. 两组对角分别相等
3.如图,已知四边形 ABCD 是平行四边形,下列结论中不正确的是( )
A. 当 AB=BC 时,它是菱形 B. 当 AC⊥BD 时,它是菱形
C. 当 ∠ABC=90° 时,它是矩形 D. 当 AC=BD 时,它是正方形
4.下列说法中,错误的是( )
A. 平行四边形的对角线互相平分 B. 菱形的对角线互相垂直平分
C. 矩形的对角线互相垂直 D. 正方形的对角线相等
5.如图,已知点P为长方形 内一点(不含边界),设 ,若 ,则( )
A. B.
C. D.
6.如图,四边形 是长方形,点 是 长线上一点, 是 上一点,并且 , .若 ,则 的度数是( )
A. B. C. 30° D.
7.如图,在 中, , 于点 , 是 的外角的平分线, 交 于点 ,则四边形 的形状是( )
A. 平行四边形 B. 矩形 C. 菱形 D. 正方形
8.如图,四边形 OABC 是矩形,A(2,1),B(0,5),点 C 在第二象限,则点 C 的坐标是( )
A. (1,3) B. (﹣1,2) C. (﹣2,﹣3) D. (﹣2,4)
9.在平面直角坐标系中,菱形ABCD的顶点的坐标A,B,C分别为(﹣2,0),(0,1),(2,0),则顶点D的坐标为( )
A. (0,﹣1) B. (﹣2,1) C. (2,1) D. (0,﹣2)
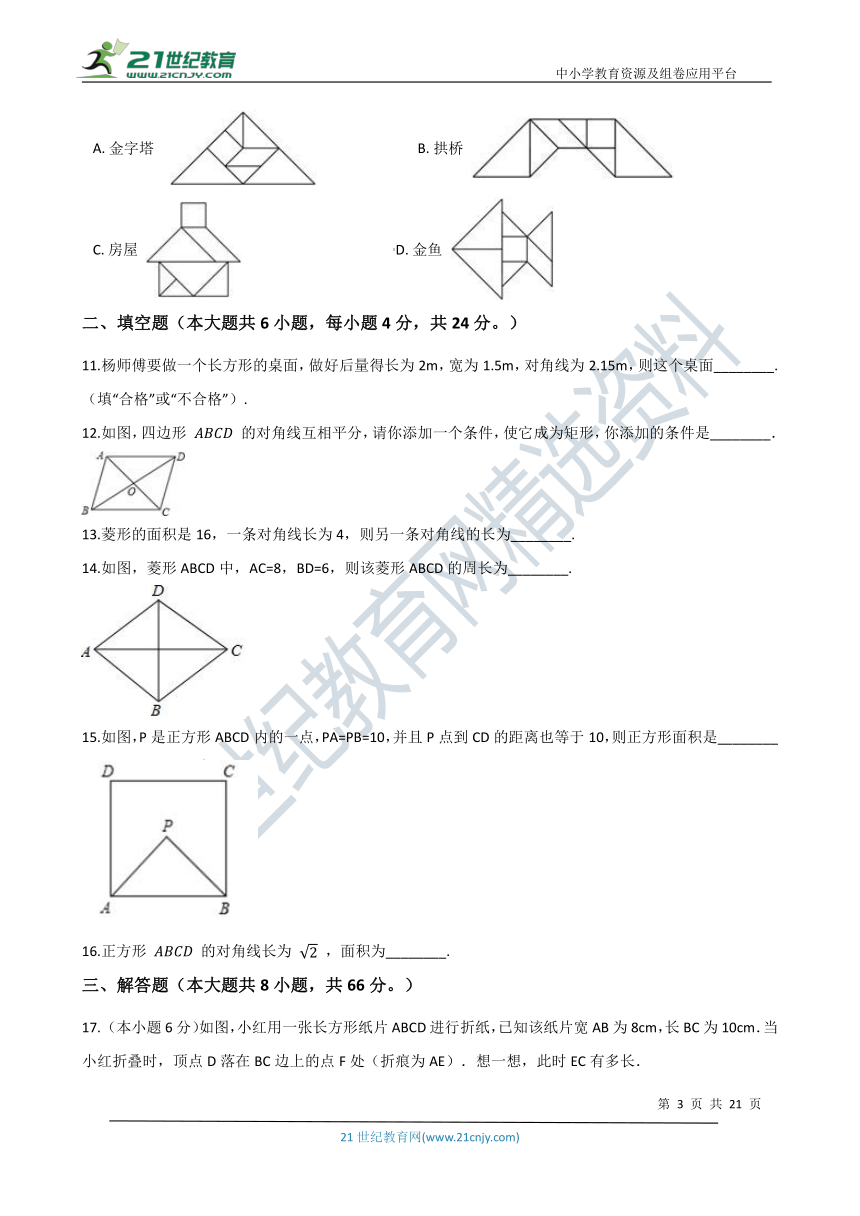
10.七巧板是我国祖先的一项卓越创造.下列四幅图中有三幅是用右图所示的七巧板拼成的,则不能用七巧板拼成的那幅图是( )
A. 金字塔 B. 拱桥
C. 房屋 D. 金鱼
二、填空题(本大题共6小题,每小题4分,共24分。)
11.杨师傅要做一个长方形的桌面,做好后量得长为2m,宽为1.5m,对角线为2.15m,则这个桌面________.(填“合格”或“不合格”).
12.如图,四边形 的对角线互相平分,请你添加一个条件,使它成为矩形,你添加的条件是________.
13.菱形的面积是16,一条对角线长为4,则另一条对角线的长为________.
14.如图,菱形ABCD中,AC=8,BD=6,则该菱形ABCD的周长为________.
15.如图,P是正方形ABCD内的一点,PA=PB=10,并且P点到CD的距离也等于10,则正方形面积是________
16.正方形 的对角线长为 ,面积为________.
三、解答题(本大题共8小题,共66分。)
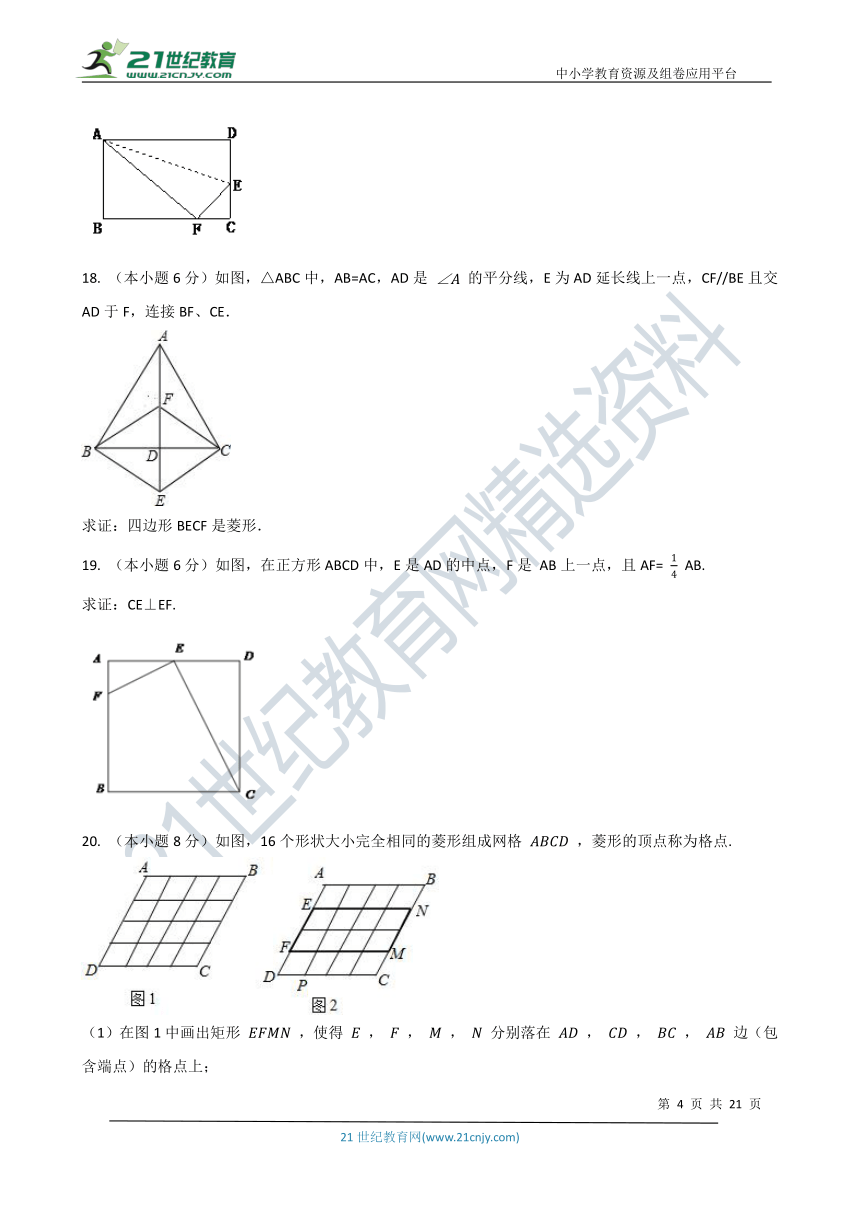
17. (本小题6分)如图,小红用一张长方形纸片ABCD进行折纸,已知该纸片宽AB为8cm,长BC为10cm.当小红折叠时,顶点D落在BC边上的点F处(折痕为AE).想一想,此时EC有多长.
18. (本小题6分)如图,△ABC中,AB=AC,AD是 的平分线,E为AD延长线上一点,CF//BE且交AD于F,连接BF、CE.
求证:四边形BECF是菱形.
19. (本小题6分)如图,在正方形ABCD中,E是AD的中点,F是 AB上一点,且AF= AB.
求证:CE⊥EF.
20. (本小题8分)如图,16个形状大小完全相同的菱形组成网格 ,菱形的顶点称为格点.
(1)在图1中画出矩形 ,使得 , , , 分别落在 , , , 边(包含端点)的格点上;
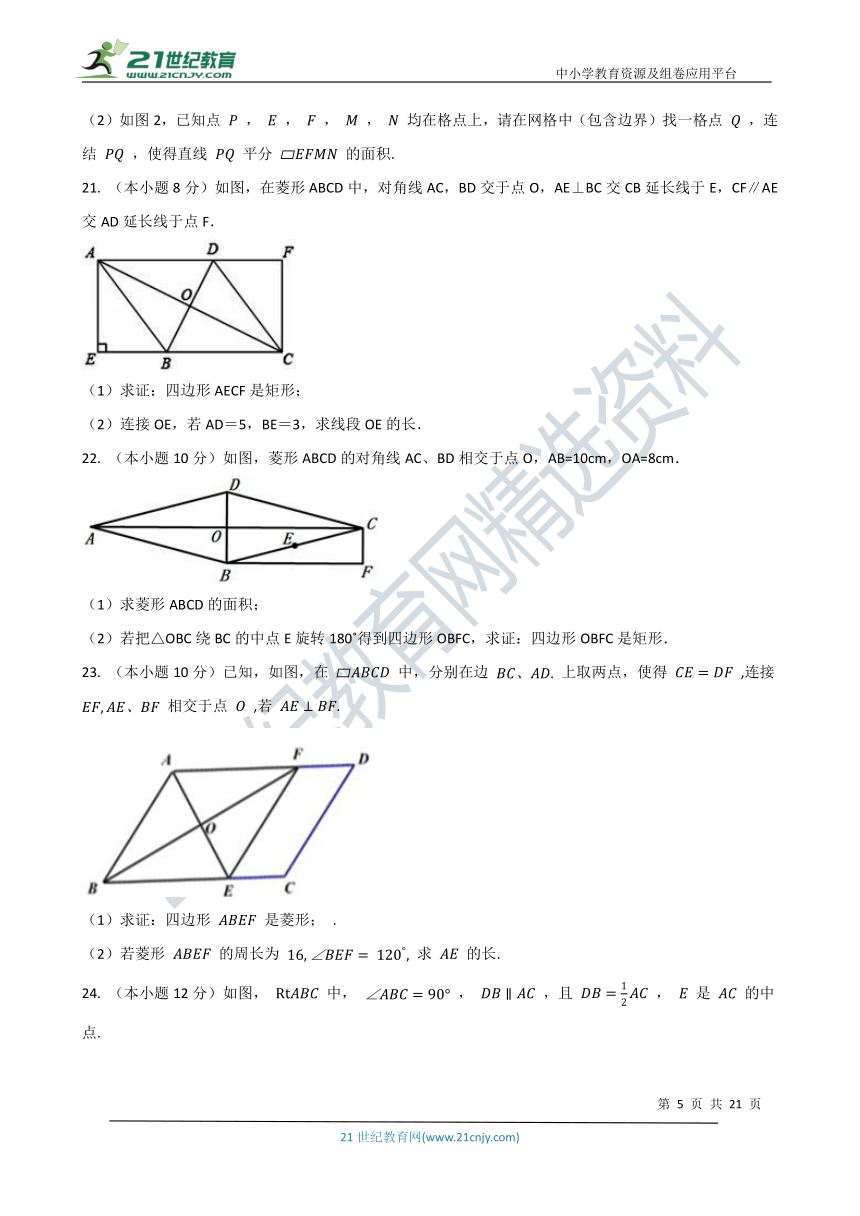
(2)如图2,已知点 , , , , 均在格点上,请在网格中(包含边界)找一格点 ,连结 ,使得直线 平分 的面积.
21. (本小题8分)如图,在菱形ABCD中,对角线AC,BD交于点O,AE⊥BC交CB延长线于E,CF∥AE交AD延长线于点F.
(1)求证:四边形AECF是矩形;
(2)连接OE,若AD=5,BE=3,求线段OE的长.
22. (本小题10分)如图,菱形ABCD的对角线AC、BD相交于点O,AB=10cm,OA=8cm.
(1)求菱形ABCD的面积;
(2)若把△OBC绕BC的中点E旋转180 得到四边形OBFC,求证:四边形OBFC是矩形.
23. (本小题10分)已知,如图,在 中,分别在边 上取两点,使得 ,连接 相交于点 ,若
(1)求证:四边形 是菱形; .
(2)若菱形 的周长为 求 的长.
24. (本小题12分)如图, 中, , ,且 , 是 的中点.
(1)求证:四边形 是菱形.
(2)如果 , ,求四边形 的面积.
(3)当 ________度时,四边形 是正方形(不证明)
答案解析部分
一、单选题
1. A
考点:菱形的判定
解:∵AB∥CD,AD∥BC,
∴四边形ABCD是平行四边形,
如下图,
若BC=CD,则平行四边形ABCD是菱形;
若AB=CD,则还是平行四边形;
若∠ADC=90°,则平行四边形ABCD是矩形;
若AD=BC,则还是平行四边形;
故答案为:A.
分析:由已知可得四边形ABCD是平行四边形,再根据菱形的判定方法即可得出结论.
2. B
考点:菱形的性质,矩形的性质
解:A、两组对边分别平行是平行四边形的基本性质,两者都具有,故A不符合题意;
B、菱形的对角线互相垂直,而矩形的对角线不一定互相垂直;故B符合题意;
C、对角线互相平分是平行四边形的基本性质,两者都具有,故C不符合题意;
D、两组对角分别相等是平行四边形的基本性质,两者都具有,故D不符合题意;
故答案为:B.
分析:菱形与矩形都是平行四边i形,故平行四边形的性质二者都具有,菱形的对角线互相垂直 ,矩形的对角线相等,逐项进行判断,即可求解.
3. D
考点:菱形的判定,矩形的判定,正方形的判定
解:由四边形ABCD 是平行四边形,
A、 当 AB=BC时,根据一组邻边相等的平行四边形是菱形,故A不符合题意;
B、 当 AC⊥BD时,根据对角线互相垂直的平行四边形是菱形,故B不符合题意;
C、 当 ∠ABC=90°时,根据有一个角是直角的平行四边形是矩形,故C不符合题意;
D、 当 AC=BD时,根据对角线相等的平行四边形是矩形,故D符合题意.
故答案为:D.
分析:根据菱形的判定方法、矩形的判定方法、正方形的判定方法逐项进行判断,即可求解.
4. C
考点:平行四边形的性质,菱形的性质,矩形的性质,正方形的性质
解:A、平行四边形的对角线互相平分,A不符合题意;
B、菱形的对角线互相垂直平分,B不符合题意;
C、矩形的对角线相等且互相平分,C符合题意;
D、正方形的对角线相等且互相垂直平分,D不符合题意;
故答案为:C.
分析:平行四边形的对角线互相平分,菱形的对角线互相垂直平分,矩形的对角线相等且互相平分,正方形的对角线相等且互相垂直平分,据此逐一判断即可.
5. A
考点:三角形内角和定理,矩形的性质
解:如图:
∵ABCD是长方形,
∴∠BAD=∠BCD=90°,
∴∠BAP=90°﹣θ1 , ∠DCP=90°﹣θ3 ,
在△ABP中,∵90°﹣θ1+θ2+80°=180°,∴θ2﹣θ1=10°①,
在△DCP中,∵90°﹣θ3+θ4+50°=180°,∴θ4﹣θ3=40°②,
由②﹣①可得:(θ4﹣θ3)﹣(θ2﹣θ1)=30°,
即(θ1+θ4)﹣(θ2+θ3)=30°.
故答案为:A.
分析:依据矩形的性质和角的和差可得∠BAP=90°﹣θ1 , ∠DCP=90°﹣θ3 , 在△ABP和△DCP中,根据三角形内角和定理可得θ2﹣θ1=10°,θ4﹣θ3=40°,两式相减即可得到答案.
6. C
考点:矩形的性质
解:∵四边形ABCD是矩形,
∴AD∥BC,∠DCB=90°,
∴∠F=∠ECB=15°,
∴∠GAF=∠F=15°,
∴∠ACF=∠AGC=∠GAF+∠F=2∠F=30°,
故答案为:C.
分析:先根据矩形的性质求出AD∥BC,∠DCB=90°,再求出∠GAF=∠F=15°,最后求解即可。
7. B
考点:等腰三角形的性质,平行四边形的判定与性质,矩形的判定
解:如图,
∵AB=AC,
∴∠ABC=∠ACB,
∴∠HAC=∠ABC+∠ACB=2∠ABC,
∵AE是∠HAC的平分线,
∴∠HAC= 2∠HAE,
∴∠HAE=∠ABC,
∴AE∥BC,
又∵AB∥DE,
∴四边形ABDE是平行四边形,
∴AE=BD,
∵AB=AC,AD⊥BC,
∴BD=DC,
∴AE=CD,
又∵AE∥DC,
∴四边形ADCE是平行四边形,
又∵AD⊥CD,
∴四边形ADCE是矩形,
故答案为:B.
分析:由等腰三角形的性质和角平分线的性质可证AE∥BC,可得四边形ABDE是平行四边形,可得AE=BD,由等腰三角形的性质可得BD=CD=AE,AD⊥CD,可得四边形ADCE是矩形.
8. D
考点:全等三角形的性质,矩形的性质,点的坐标与象限的关系
解:过C作CE⊥y轴与E,过A作AF⊥y轴于F.
∴∠CEO=∠AFB=90°
∵四边形ABCO为矩形
∴AB=OC,AB OC
∴∠ABF=∠COE
∴△OCE≌△BAF(AAS)
同理可得
∴△BCE≌△OAF(AAS)
∴CE=AF,OE=BF,BE=OF
∵A(2,1),B(0,5)
∴AF=CE=2,BE=OF=1,OB=5
∴OE=4,
∴点C的坐标为(-2,4)
故答案为:D.
分析:先分别过C和A作y轴的垂线,构造两组全等三角形,用矩形的相关性质即可证明,再利用两组三角形全等对应边相等CE=AF、BE=OF,结合已知坐标就能求得C点坐标.
9. A
考点:坐标与图形性质,菱形的性质
解:如图所示,
∵菱形ABCD的对角线互相垂直平分,A、B、C分别为(﹣2,0),(0,1),(2,0),
∴D(0,﹣1).
故答案为:A.
分析:根据题意画出图形,根据菱形的对角线互相垂直平分即可得出结论.
10. C
考点:七巧板
解:如图,
设正方形的边长为2,从而可知①②都是直角边为 的等腰直角三角形;
③⑥都是直角边为 的等腰直角三角形;
④是两边长分别为1和 的平行四边形;
④是边长为 的正方形;
⑦是直角边为1的等腰直角三角形,
观察图形可知,C中等腰直角三角形的直角边与平行四边形的长边不可能重合,故七巧板构不成图案C.
故答案为:C.
分析:七巧板是由:五个等腰直角三角形,有大、小两对全等三角形;一个正方形;一个平行四边形,设正方形的边长为2,根据这些图形的性质分别算出各个图形的边长,故C中等腰直角三角形的直角边与平行四边形的长边不可能重合,从而得出答案。
二、填空题
11. 不合格
考点:勾股定理的逆定理,矩形的判定
解:如图:
∵22+1.52=6.25 2.152 ,
即:AD2+DC2 AC2 ,
∴∠D 90°,
∴四边形ABCD不是矩形,
∴这个桌面不合格.
故答案为:不合格.
分析:只要算出桌面的长与宽的平方和是否等于对角线的平方,如果不相等,长、宽、对角线构成的就不是直角三角形,可得此桌面不合格.
12. (答案不唯一)
考点:矩形的判定
解:可添加AC=BD,
∵四边形ABCD的对角线互相平分,
∴四边形ABCD是平行四边形,
∵AC=BD,
∴四边形ABCD是矩形,
故答案为AC=BD(答案不唯一).
分析:由四边形ABCD的对角线互相平分,可得四边形ABCD是平行四边形,再添加AC=BD,可根据对角线相等的平行四边形是矩形证明四边形ABCD是矩形.
13. 8
考点:菱形的性质
解:设另一条对角线的长为x,则有
=16,
解得:x=8,
故答案为8.
分析:根据菱形的面积等于对角线乘积的一半进行计算即可求得.
14. 20
考点:勾股定理,菱形的性质
解:如图,
∵菱形对角线互相垂直平分,AC=8,BD=6,
∴BO=OD=3,AO=OC=4,
∴AB= =5,
故该菱形ABCD的周长为20,
故答案为:20.
分析:根据菱形对角线互相垂直平分的性质,可以求得BO=OD,AO=OC,在Rt△AOB中,根据勾股定理可以求得AB的长,即可求菱形ABCD的周长.
15. 256
考点:勾股定理,正方形的性质
解:过P作EF⊥AB于E,交CD于F,则PF⊥CD
所以PF=PA=PB=10,E为AB中点
设PE=x,则AB=AD=10+x
所以AE= AB= (10+x)
在Rt△PAE中,PA2=PE2+AE2
所以102=x2+[ (10+x)]2所以x=6
所以正方形ABCD面积=AB2=(10+6)2=256.
故填:256.
分析:设PE=x,根据正方形各边相等的等量关系式,即可得到FP+PE=AB的等量关系式,再列出方程求解即可。
16. 1
考点:正方形的性质
解:如图,
四边形 为正方形,
, ,
正方形 的面积 ,
故答案为:1.
分析:根据正方形的对角线相等且互相垂直,正方形是特殊的菱形,菱形的面积等于对角线乘积的一半进行求解即可.
三、解答题
17. 解:∵四边形ABCD为矩形,∴AB=CD=8,BC=AD=10,∠B=∠C=90°.
∵长方形纸片ABCD折纸,顶点D落在BC边上的点F处(折痕为AE),
∴AF=AD=10,DE=EF,
在Rt△ABF中,AB=8,AF=10,∴BF=
∴CF=BC﹣BF=4.
设CE=x,则DE=EF=8﹣x,
在Rt△CEF中,∵CF2+CE2=EF2 ,
∴42+x2=(8﹣x)2 , 解得x=3
∴EC的长为3cm.
考点:勾股定理,矩形的性质,轴对称的性质,解含括号的一元一次方程
分析:根据矩形的性质得AB=CD=8,BC=AD=10,∠B=∠C=90°,再根据折叠的性质得AF=AD=10,DE=EF,在Rt△ABF中,利用勾股定理计算出BF=6,则CF=BC﹣BF=4,设CE=x,则DE=EF=8﹣x,在Rt△CEF中利用勾股定理得到∴42+x2=(8﹣x)2 , 然后解方程即可.
18. 证明:∵AB=AC,AD是角平分线,
∴BD=CD,
∵CF∥BE,
∴∠DBE=∠DCF,
在△BDE和△CDF中,
,
∴△BDE≌△CDF(ASA),
∴CF=BE,
又∵CF∥BE,
∴四边形BFCE是平行四边形;
∵AB=AC,AD是角平分线,
∴AD⊥BC,
又∵四边形BFCE是平行四边形,
∴四边形BFCE是菱形.
考点:菱形的判定
分析:利用ASA易证得△BDE≌△CDF,推出CF=BE,证得四边形BFCE是平行四边形;根据对角线互相垂直的平行四边形是菱形,即可证得四边形BFCE是菱形.
19. 证明:连接 ,
∵ 为正方形
∴ , .
设
∵E是 的中点,且
∴ ,
∴ .
在 中,由勾股定理可得
同理可得:
.
∵
∴ 为直角三角形
∴
∴ .
考点:勾股定理,勾股定理的逆定理,正方形的性质
分析:利用正方形的性质得出 , ,设出边长为 ,进一步利用勾股定理求得 、 、 的长,再利用勾股定理逆定理判定即可.
20. (1)解:矩形MNEF如图所示.
(2)解:如图2中,点Q即为所求.
考点:平行四边形的性质,菱形的性质,矩形的判定
分析:(1)根据菱形的性质及矩形的判定方法作出图形即可(答案不唯一);
(2)根据平行四边形的中心对称性,故直线PQ经过平行四边形的中心即可.
21. (1)证明:∵四边形ABCD为菱形,
∴AD∥BC,
即AF∥EC,
∵CF∥AE,
∴四边形AECF是平行四边形,
∵AE⊥BC,
∴平行四边形AECF是矩形。
(2)解:∵四边形ABCD为菱形,四边形AECF为矩形,且BE=3,AD=5,
∴AB=BC=AD=5,DF=BE=3,
∴AE= =4,
CE=BE+BC=8,
∴ ,
∵对角线AC,BD交于点O,
∴OA=OC,
∵四边形AECF为矩形,
∴点O是对角线AC与EF的交点,
∴ .
考点:勾股定理,矩形的判定与性质
分析:(1)根据菱形的性质得到AD∥BC,推出四边形AECF是平行四边形,根据矩形的判定定理即可得出结论;(2)根据已知条件得到AE=4,CE=8,求得AC= ,从而得出答案.
22. (1)∵四边形ABCD是菱形
∴AC⊥BD .
在直角三角形AOB中,AB=10cm,OA=8cm
OB= = =6cm.
∴AC=2OA=2×8=16cm ;BD=2OB=2×6=12cm
∴菱形ABCD的面积= ×AC×BD= ×16×12=96cm2 .
(2)∵四边形ABCD是菱形
∴AC⊥BD
∴∠BOC=
∴在Rt△BOC中,∠OBC+∠OCB= .
又∵把△OBC绕BC的中点E旋转 得到四边形OBFC
∴∠F=∠BOC= ,∠OBC=∠BCF
∴∠BCF+∠OCB= ,即∠OCF= .
∴四边形OBFC是矩形(有三个角是直角的四边形是矩形).
考点:菱形的性质,矩形的判定
分析:(1)利用勾股定理,求出OB,继而求出菱形的面积,即可.(2)求出四边形OBFC的各个角的大小,利用矩形的判定定理,即可证明.
23. (1)证明:∵四边形 是平行四边形,
,
又∵ ,
,
,
四边形 是平行四边形,
又∵ ,
∴四边形 是菱形;
(2)解:∵菱形 的周长为 ,
,
又∵ ,
,
为等边三角形,
,
.
考点:等边三角形的判定与性质,平行四边形的性质,菱形的判定
分析:(1)根据已知可得 ,故ABEF为平行四边形,再根据对角线互相垂直即可得证;(2)根据菱形的性质可证得 为等边三角形,即可求解.
24. (1)证明:∵∠ABC=90°,E是AC的中点,
∴EB=EC=EA= AC,
∵DB= AC,
∴AE=DB=EB,
∵DB∥AC,
∴四边形ADBE是平行四边形,
∵DB=EB,
∴四边形ADBE是菱形
(2)解:∵在Rt△ABC中,AB=8,BC=6,
∴S△ABC= ×BC×AB= ×6×8=24,
∵E是AC的中点,
∴S△ABE= S△ABC= ×24=12,
∵AB是菱形ADBE的对角线,
∴S四边形ADBE=2S△ABE=2×12=24
(3)45
考点:三角形的面积,菱形的判定,正方形的判定
解:(3)当∠C=45°时,四边形ADBE是正方形,
∵∠ABC=90°,∠C=45°,
∴∠BAC=45°=∠C,
∵四边形ADBE是菱形,
∴∠DAE=2∠BAC=90°,
∴四边形ADBE是正方形.
故答案为:45.
分析:(1)根据直角三角形斜边上的中线等于斜边的一半得出EB=EC=EA,根据一组对边平行且相等可证四边形ADBE是平行四边形,最后利用邻边相等的平行四边形是菱形进行证明;
(2)先求出Rt△ABC的面积,根据E是AC的中点可得△ABE的面积,最后根据S四边形ADBE=2S△ABE进行求解;
(3)根据有一个角为90°的菱形是正方形进行求证.
21世纪教育网(www.21cnjy.com)
初中数学浙教版八年级下册第五章 特殊平行四边形 章末检测(基础篇)
一、单选题(本大题共10小题,每小题3分,共30分。)
1.在四边形ABCD中,AB∥CD,AD∥BC,如果再添加一个条件,即可推出该四边形是菱形,这个条件可以是( )
A. BC=CD B. AB=CD C. ∠D=90° D. AD=BC
2.菱形具有而矩形不具有的性质是( )
A. 两组对边分别平行 B. 对角线互相垂直 C. 对角线互相平分 D. 两组对角分别相等
3.如图,已知四边形 ABCD 是平行四边形,下列结论中不正确的是( )
A. 当 AB=BC 时,它是菱形 B. 当 AC⊥BD 时,它是菱形
C. 当 ∠ABC=90° 时,它是矩形 D. 当 AC=BD 时,它是正方形
4.下列说法中,错误的是( )
A. 平行四边形的对角线互相平分 B. 菱形的对角线互相垂直平分
C. 矩形的对角线互相垂直 D. 正方形的对角线相等
5.如图,已知点P为长方形 内一点(不含边界),设 ,若 ,则( )
A. B.
C. D.
6.如图,四边形 是长方形,点 是 长线上一点, 是 上一点,并且 , .若 ,则 的度数是( )
A. B. C. 30° D.
7.如图,在 中, , 于点 , 是 的外角的平分线, 交 于点 ,则四边形 的形状是( )
A. 平行四边形 B. 矩形 C. 菱形 D. 正方形
8.如图,四边形 OABC 是矩形,A(2,1),B(0,5),点 C 在第二象限,则点 C 的坐标是( )
A. (1,3) B. (﹣1,2) C. (﹣2,﹣3) D. (﹣2,4)
9.在平面直角坐标系中,菱形ABCD的顶点的坐标A,B,C分别为(﹣2,0),(0,1),(2,0),则顶点D的坐标为( )
A. (0,﹣1) B. (﹣2,1) C. (2,1) D. (0,﹣2)
10.七巧板是我国祖先的一项卓越创造.下列四幅图中有三幅是用右图所示的七巧板拼成的,则不能用七巧板拼成的那幅图是( )
A. 金字塔 B. 拱桥
C. 房屋 D. 金鱼
二、填空题(本大题共6小题,每小题4分,共24分。)
11.杨师傅要做一个长方形的桌面,做好后量得长为2m,宽为1.5m,对角线为2.15m,则这个桌面________.(填“合格”或“不合格”).
12.如图,四边形 的对角线互相平分,请你添加一个条件,使它成为矩形,你添加的条件是________.
13.菱形的面积是16,一条对角线长为4,则另一条对角线的长为________.
14.如图,菱形ABCD中,AC=8,BD=6,则该菱形ABCD的周长为________.
15.如图,P是正方形ABCD内的一点,PA=PB=10,并且P点到CD的距离也等于10,则正方形面积是________
16.正方形 的对角线长为 ,面积为________.
三、解答题(本大题共8小题,共66分。)
17. (本小题6分)如图,小红用一张长方形纸片ABCD进行折纸,已知该纸片宽AB为8cm,长BC为10cm.当小红折叠时,顶点D落在BC边上的点F处(折痕为AE).想一想,此时EC有多长.
18. (本小题6分)如图,△ABC中,AB=AC,AD是 的平分线,E为AD延长线上一点,CF//BE且交AD于F,连接BF、CE.
求证:四边形BECF是菱形.
19. (本小题6分)如图,在正方形ABCD中,E是AD的中点,F是 AB上一点,且AF= AB.
求证:CE⊥EF.
20. (本小题8分)如图,16个形状大小完全相同的菱形组成网格 ,菱形的顶点称为格点.
(1)在图1中画出矩形 ,使得 , , , 分别落在 , , , 边(包含端点)的格点上;
(2)如图2,已知点 , , , , 均在格点上,请在网格中(包含边界)找一格点 ,连结 ,使得直线 平分 的面积.
21. (本小题8分)如图,在菱形ABCD中,对角线AC,BD交于点O,AE⊥BC交CB延长线于E,CF∥AE交AD延长线于点F.
(1)求证:四边形AECF是矩形;
(2)连接OE,若AD=5,BE=3,求线段OE的长.
22. (本小题10分)如图,菱形ABCD的对角线AC、BD相交于点O,AB=10cm,OA=8cm.
(1)求菱形ABCD的面积;
(2)若把△OBC绕BC的中点E旋转180 得到四边形OBFC,求证:四边形OBFC是矩形.
23. (本小题10分)已知,如图,在 中,分别在边 上取两点,使得 ,连接 相交于点 ,若
(1)求证:四边形 是菱形; .
(2)若菱形 的周长为 求 的长.
24. (本小题12分)如图, 中, , ,且 , 是 的中点.
(1)求证:四边形 是菱形.
(2)如果 , ,求四边形 的面积.
(3)当 ________度时,四边形 是正方形(不证明)
答案解析部分
一、单选题
1. A
考点:菱形的判定
解:∵AB∥CD,AD∥BC,
∴四边形ABCD是平行四边形,
如下图,
若BC=CD,则平行四边形ABCD是菱形;
若AB=CD,则还是平行四边形;
若∠ADC=90°,则平行四边形ABCD是矩形;
若AD=BC,则还是平行四边形;
故答案为:A.
分析:由已知可得四边形ABCD是平行四边形,再根据菱形的判定方法即可得出结论.
2. B
考点:菱形的性质,矩形的性质
解:A、两组对边分别平行是平行四边形的基本性质,两者都具有,故A不符合题意;
B、菱形的对角线互相垂直,而矩形的对角线不一定互相垂直;故B符合题意;
C、对角线互相平分是平行四边形的基本性质,两者都具有,故C不符合题意;
D、两组对角分别相等是平行四边形的基本性质,两者都具有,故D不符合题意;
故答案为:B.
分析:菱形与矩形都是平行四边i形,故平行四边形的性质二者都具有,菱形的对角线互相垂直 ,矩形的对角线相等,逐项进行判断,即可求解.
3. D
考点:菱形的判定,矩形的判定,正方形的判定
解:由四边形ABCD 是平行四边形,
A、 当 AB=BC时,根据一组邻边相等的平行四边形是菱形,故A不符合题意;
B、 当 AC⊥BD时,根据对角线互相垂直的平行四边形是菱形,故B不符合题意;
C、 当 ∠ABC=90°时,根据有一个角是直角的平行四边形是矩形,故C不符合题意;
D、 当 AC=BD时,根据对角线相等的平行四边形是矩形,故D符合题意.
故答案为:D.
分析:根据菱形的判定方法、矩形的判定方法、正方形的判定方法逐项进行判断,即可求解.
4. C
考点:平行四边形的性质,菱形的性质,矩形的性质,正方形的性质
解:A、平行四边形的对角线互相平分,A不符合题意;
B、菱形的对角线互相垂直平分,B不符合题意;
C、矩形的对角线相等且互相平分,C符合题意;
D、正方形的对角线相等且互相垂直平分,D不符合题意;
故答案为:C.
分析:平行四边形的对角线互相平分,菱形的对角线互相垂直平分,矩形的对角线相等且互相平分,正方形的对角线相等且互相垂直平分,据此逐一判断即可.
5. A
考点:三角形内角和定理,矩形的性质
解:如图:
∵ABCD是长方形,
∴∠BAD=∠BCD=90°,
∴∠BAP=90°﹣θ1 , ∠DCP=90°﹣θ3 ,
在△ABP中,∵90°﹣θ1+θ2+80°=180°,∴θ2﹣θ1=10°①,
在△DCP中,∵90°﹣θ3+θ4+50°=180°,∴θ4﹣θ3=40°②,
由②﹣①可得:(θ4﹣θ3)﹣(θ2﹣θ1)=30°,
即(θ1+θ4)﹣(θ2+θ3)=30°.
故答案为:A.
分析:依据矩形的性质和角的和差可得∠BAP=90°﹣θ1 , ∠DCP=90°﹣θ3 , 在△ABP和△DCP中,根据三角形内角和定理可得θ2﹣θ1=10°,θ4﹣θ3=40°,两式相减即可得到答案.
6. C
考点:矩形的性质
解:∵四边形ABCD是矩形,
∴AD∥BC,∠DCB=90°,
∴∠F=∠ECB=15°,
∴∠GAF=∠F=15°,
∴∠ACF=∠AGC=∠GAF+∠F=2∠F=30°,
故答案为:C.
分析:先根据矩形的性质求出AD∥BC,∠DCB=90°,再求出∠GAF=∠F=15°,最后求解即可。
7. B
考点:等腰三角形的性质,平行四边形的判定与性质,矩形的判定
解:如图,
∵AB=AC,
∴∠ABC=∠ACB,
∴∠HAC=∠ABC+∠ACB=2∠ABC,
∵AE是∠HAC的平分线,
∴∠HAC= 2∠HAE,
∴∠HAE=∠ABC,
∴AE∥BC,
又∵AB∥DE,
∴四边形ABDE是平行四边形,
∴AE=BD,
∵AB=AC,AD⊥BC,
∴BD=DC,
∴AE=CD,
又∵AE∥DC,
∴四边形ADCE是平行四边形,
又∵AD⊥CD,
∴四边形ADCE是矩形,
故答案为:B.
分析:由等腰三角形的性质和角平分线的性质可证AE∥BC,可得四边形ABDE是平行四边形,可得AE=BD,由等腰三角形的性质可得BD=CD=AE,AD⊥CD,可得四边形ADCE是矩形.
8. D
考点:全等三角形的性质,矩形的性质,点的坐标与象限的关系
解:过C作CE⊥y轴与E,过A作AF⊥y轴于F.
∴∠CEO=∠AFB=90°
∵四边形ABCO为矩形
∴AB=OC,AB OC
∴∠ABF=∠COE
∴△OCE≌△BAF(AAS)
同理可得
∴△BCE≌△OAF(AAS)
∴CE=AF,OE=BF,BE=OF
∵A(2,1),B(0,5)
∴AF=CE=2,BE=OF=1,OB=5
∴OE=4,
∴点C的坐标为(-2,4)
故答案为:D.
分析:先分别过C和A作y轴的垂线,构造两组全等三角形,用矩形的相关性质即可证明,再利用两组三角形全等对应边相等CE=AF、BE=OF,结合已知坐标就能求得C点坐标.
9. A
考点:坐标与图形性质,菱形的性质
解:如图所示,
∵菱形ABCD的对角线互相垂直平分,A、B、C分别为(﹣2,0),(0,1),(2,0),
∴D(0,﹣1).
故答案为:A.
分析:根据题意画出图形,根据菱形的对角线互相垂直平分即可得出结论.
10. C
考点:七巧板
解:如图,
设正方形的边长为2,从而可知①②都是直角边为 的等腰直角三角形;
③⑥都是直角边为 的等腰直角三角形;
④是两边长分别为1和 的平行四边形;
④是边长为 的正方形;
⑦是直角边为1的等腰直角三角形,
观察图形可知,C中等腰直角三角形的直角边与平行四边形的长边不可能重合,故七巧板构不成图案C.
故答案为:C.
分析:七巧板是由:五个等腰直角三角形,有大、小两对全等三角形;一个正方形;一个平行四边形,设正方形的边长为2,根据这些图形的性质分别算出各个图形的边长,故C中等腰直角三角形的直角边与平行四边形的长边不可能重合,从而得出答案。
二、填空题
11. 不合格
考点:勾股定理的逆定理,矩形的判定
解:如图:
∵22+1.52=6.25 2.152 ,
即:AD2+DC2 AC2 ,
∴∠D 90°,
∴四边形ABCD不是矩形,
∴这个桌面不合格.
故答案为:不合格.
分析:只要算出桌面的长与宽的平方和是否等于对角线的平方,如果不相等,长、宽、对角线构成的就不是直角三角形,可得此桌面不合格.
12. (答案不唯一)
考点:矩形的判定
解:可添加AC=BD,
∵四边形ABCD的对角线互相平分,
∴四边形ABCD是平行四边形,
∵AC=BD,
∴四边形ABCD是矩形,
故答案为AC=BD(答案不唯一).
分析:由四边形ABCD的对角线互相平分,可得四边形ABCD是平行四边形,再添加AC=BD,可根据对角线相等的平行四边形是矩形证明四边形ABCD是矩形.
13. 8
考点:菱形的性质
解:设另一条对角线的长为x,则有
=16,
解得:x=8,
故答案为8.
分析:根据菱形的面积等于对角线乘积的一半进行计算即可求得.
14. 20
考点:勾股定理,菱形的性质
解:如图,
∵菱形对角线互相垂直平分,AC=8,BD=6,
∴BO=OD=3,AO=OC=4,
∴AB= =5,
故该菱形ABCD的周长为20,
故答案为:20.
分析:根据菱形对角线互相垂直平分的性质,可以求得BO=OD,AO=OC,在Rt△AOB中,根据勾股定理可以求得AB的长,即可求菱形ABCD的周长.
15. 256
考点:勾股定理,正方形的性质
解:过P作EF⊥AB于E,交CD于F,则PF⊥CD
所以PF=PA=PB=10,E为AB中点
设PE=x,则AB=AD=10+x
所以AE= AB= (10+x)
在Rt△PAE中,PA2=PE2+AE2
所以102=x2+[ (10+x)]2所以x=6
所以正方形ABCD面积=AB2=(10+6)2=256.
故填:256.
分析:设PE=x,根据正方形各边相等的等量关系式,即可得到FP+PE=AB的等量关系式,再列出方程求解即可。
16. 1
考点:正方形的性质
解:如图,
四边形 为正方形,
, ,
正方形 的面积 ,
故答案为:1.
分析:根据正方形的对角线相等且互相垂直,正方形是特殊的菱形,菱形的面积等于对角线乘积的一半进行求解即可.
三、解答题
17. 解:∵四边形ABCD为矩形,∴AB=CD=8,BC=AD=10,∠B=∠C=90°.
∵长方形纸片ABCD折纸,顶点D落在BC边上的点F处(折痕为AE),
∴AF=AD=10,DE=EF,
在Rt△ABF中,AB=8,AF=10,∴BF=
∴CF=BC﹣BF=4.
设CE=x,则DE=EF=8﹣x,
在Rt△CEF中,∵CF2+CE2=EF2 ,
∴42+x2=(8﹣x)2 , 解得x=3
∴EC的长为3cm.
考点:勾股定理,矩形的性质,轴对称的性质,解含括号的一元一次方程
分析:根据矩形的性质得AB=CD=8,BC=AD=10,∠B=∠C=90°,再根据折叠的性质得AF=AD=10,DE=EF,在Rt△ABF中,利用勾股定理计算出BF=6,则CF=BC﹣BF=4,设CE=x,则DE=EF=8﹣x,在Rt△CEF中利用勾股定理得到∴42+x2=(8﹣x)2 , 然后解方程即可.
18. 证明:∵AB=AC,AD是角平分线,
∴BD=CD,
∵CF∥BE,
∴∠DBE=∠DCF,
在△BDE和△CDF中,
,
∴△BDE≌△CDF(ASA),
∴CF=BE,
又∵CF∥BE,
∴四边形BFCE是平行四边形;
∵AB=AC,AD是角平分线,
∴AD⊥BC,
又∵四边形BFCE是平行四边形,
∴四边形BFCE是菱形.
考点:菱形的判定
分析:利用ASA易证得△BDE≌△CDF,推出CF=BE,证得四边形BFCE是平行四边形;根据对角线互相垂直的平行四边形是菱形,即可证得四边形BFCE是菱形.
19. 证明:连接 ,
∵ 为正方形
∴ , .
设
∵E是 的中点,且
∴ ,
∴ .
在 中,由勾股定理可得
同理可得:
.
∵
∴ 为直角三角形
∴
∴ .
考点:勾股定理,勾股定理的逆定理,正方形的性质
分析:利用正方形的性质得出 , ,设出边长为 ,进一步利用勾股定理求得 、 、 的长,再利用勾股定理逆定理判定即可.
20. (1)解:矩形MNEF如图所示.
(2)解:如图2中,点Q即为所求.
考点:平行四边形的性质,菱形的性质,矩形的判定
分析:(1)根据菱形的性质及矩形的判定方法作出图形即可(答案不唯一);
(2)根据平行四边形的中心对称性,故直线PQ经过平行四边形的中心即可.
21. (1)证明:∵四边形ABCD为菱形,
∴AD∥BC,
即AF∥EC,
∵CF∥AE,
∴四边形AECF是平行四边形,
∵AE⊥BC,
∴平行四边形AECF是矩形。
(2)解:∵四边形ABCD为菱形,四边形AECF为矩形,且BE=3,AD=5,
∴AB=BC=AD=5,DF=BE=3,
∴AE= =4,
CE=BE+BC=8,
∴ ,
∵对角线AC,BD交于点O,
∴OA=OC,
∵四边形AECF为矩形,
∴点O是对角线AC与EF的交点,
∴ .
考点:勾股定理,矩形的判定与性质
分析:(1)根据菱形的性质得到AD∥BC,推出四边形AECF是平行四边形,根据矩形的判定定理即可得出结论;(2)根据已知条件得到AE=4,CE=8,求得AC= ,从而得出答案.
22. (1)∵四边形ABCD是菱形
∴AC⊥BD .
在直角三角形AOB中,AB=10cm,OA=8cm
OB= = =6cm.
∴AC=2OA=2×8=16cm ;BD=2OB=2×6=12cm
∴菱形ABCD的面积= ×AC×BD= ×16×12=96cm2 .
(2)∵四边形ABCD是菱形
∴AC⊥BD
∴∠BOC=
∴在Rt△BOC中,∠OBC+∠OCB= .
又∵把△OBC绕BC的中点E旋转 得到四边形OBFC
∴∠F=∠BOC= ,∠OBC=∠BCF
∴∠BCF+∠OCB= ,即∠OCF= .
∴四边形OBFC是矩形(有三个角是直角的四边形是矩形).
考点:菱形的性质,矩形的判定
分析:(1)利用勾股定理,求出OB,继而求出菱形的面积,即可.(2)求出四边形OBFC的各个角的大小,利用矩形的判定定理,即可证明.
23. (1)证明:∵四边形 是平行四边形,
,
又∵ ,
,
,
四边形 是平行四边形,
又∵ ,
∴四边形 是菱形;
(2)解:∵菱形 的周长为 ,
,
又∵ ,
,
为等边三角形,
,
.
考点:等边三角形的判定与性质,平行四边形的性质,菱形的判定
分析:(1)根据已知可得 ,故ABEF为平行四边形,再根据对角线互相垂直即可得证;(2)根据菱形的性质可证得 为等边三角形,即可求解.
24. (1)证明:∵∠ABC=90°,E是AC的中点,
∴EB=EC=EA= AC,
∵DB= AC,
∴AE=DB=EB,
∵DB∥AC,
∴四边形ADBE是平行四边形,
∵DB=EB,
∴四边形ADBE是菱形
(2)解:∵在Rt△ABC中,AB=8,BC=6,
∴S△ABC= ×BC×AB= ×6×8=24,
∵E是AC的中点,
∴S△ABE= S△ABC= ×24=12,
∵AB是菱形ADBE的对角线,
∴S四边形ADBE=2S△ABE=2×12=24
(3)45
考点:三角形的面积,菱形的判定,正方形的判定
解:(3)当∠C=45°时,四边形ADBE是正方形,
∵∠ABC=90°,∠C=45°,
∴∠BAC=45°=∠C,
∵四边形ADBE是菱形,
∴∠DAE=2∠BAC=90°,
∴四边形ADBE是正方形.
故答案为:45.
分析:(1)根据直角三角形斜边上的中线等于斜边的一半得出EB=EC=EA,根据一组对边平行且相等可证四边形ADBE是平行四边形,最后利用邻边相等的平行四边形是菱形进行证明;
(2)先求出Rt△ABC的面积,根据E是AC的中点可得△ABE的面积,最后根据S四边形ADBE=2S△ABE进行求解;
(3)根据有一个角为90°的菱形是正方形进行求证.
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
