第六章 反比例函数章末检测题(基础篇含解析)
文档属性
| 名称 | 第六章 反比例函数章末检测题(基础篇含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1005.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-11 00:00:00 | ||
图片预览




文档简介
初中数学浙教版八年级下册第六章 反比例函数 章末检测(基础篇)
一、单选题(本大题共10小题,每小题3分,共30分。)
1.在下列函数中,y是x的反比例函数的是( )
A.?y=x-1?????????????????????????????B.?y= 8x2?????????????????????????????C.?y=-2x-1?????????????????????????????D.?yx =2
2.已知某用电器的输出功率为P、电阻为R,通过的电流为I,当P为定值时,下面说法正确的是(??? )
A.?I 是 R 的正比例函数??????????????????????????????????????????B.?I2 是 R 的正比例函数
C.?I 是 R 的反比例函数??????????????????????????????????????????D.?I2 是 R 的反比例函数
3.已知点A(a,m),B(a﹣1,n),C(3,﹣1)在反比例函数y= kx ?的图象上.若a>1,则m,n的大小关系是(?? )
A.?m<n???????????????????????????B.?m>n???????????????????????????C.?m=n???????????????????????????D.?m,n的大小不确定
4.某物体对地面的压力为定值,物体对地面的压强 P(Pa) 与受力面积 S(m2) 之间的函数关系如图所示,这一函数表达式为(?? )
A.?P=20S?????????????????????????????B.?P=200S?????????????????????????????C.?S=20P?????????????????????????????D.?S=200P
5.若 y=m(m-3)x 是反比例函数,则m满足的条件是(?? )
??A.?m≠0????????????????????????????B.?m=3????????????????????????????C.?m=3或m=0????????????????????????????D.?m≠3且m≠0
6.在已知反比例函数 y=kx (k为常数)的图象上有三点 A(x1,-2) , B(x2,a) , C(x3,3) ,若 x3A.?a>3????????????????????????B.?a<-2????????????????????????C.?a>3 或 a<-2????????????????????????D.?-27.如图,直线 y=n 交y轴于点A,交双曲线 y=kx(x>0) 于点B,将直线 y=n 向下平移4个单位长度后与y轴交于点C,交双曲线 y=kx(x>0) 于点D,若 ABCD=13 ,则n的值( )
?
A.?4???????????????????????????????????????????B.?6???????????????????????????????????????????C.?2???????????????????????????????????????????D.?5
8.反比例函数 y=m-2x ( m 为常数)的图象位于第一、三象限,则m的取值范围是( )
A.?m>0??????????????????????????????????B.?m>2??????????????????????????????????C.?m<0??????????????????????????????????D.?m<2
9.如图,函数 y=kx 与 y=-kx+1(k≠0) 在同一平面直角坐标系中的大致图象是(?? )
A.??????????????????B.??????????????????C.??????????????????D.?
10.关于反比例函数y= 8x ,下列说法不正确的是(?? )
A.?函数图象分别位于第一、第三象限??????????????????????B.?函数图象关于原点中心对称
C.?当x>0时,y随x的增大而增大?????????????????????????????D.?当﹣8<x<﹣1时,﹣8<y<﹣1
二、填空题(本大题共6小题,每小题4分,共24分。)
11.函数y= 1x-1 的自变量x的取值范围是________?。
12.反比例函数y= 18x 的比例系数为________.
13.写出一个反比例函数y= kx (k≠0),使它的图象在每个象限内,y的值随x值的增大而增大,这个函数的解析式为________.
14.近视眼镜的度数y(度)与镜片焦距x(m)成反比例,已知400度近视眼镜镜片的焦距为0.25m,则眼镜度数与镜片焦距之间的函数关系式为________.
15.如图,点A是反比例函数y= kx (k≠0)图象上第二象限内的一点,若△ABO的面积为3,则k的值为________
16.若反比例函数y1= kx (k>0,x>0)的图象与直线y2=x﹣1在第一象限内的交点为A,点A的横坐标为m,且满足2<m<3,则k的取值范围是________.
三、解答题(本大题共8小题,共66分。)
17. (本小题6分)已知x与y成反比例,且当x= -34 时,y= 43
(1)求y关于x的函数表达式
(2)当x= -23 时,y的值是多少?
18. (本小题6分)已知点A(m,m+1),B(m+3,m﹣1)都在反比例函数y= kx 的图象上,求m的值及反比例函数的解析式.
19. (本小题6分)设面积为 20cm2 的平行四边形的一边长为 a cm ,这条边上的高为 h cm .求 h 关于 a 的函数解析式(写出自变量 a 的取值范围)并求当 h=5 时, a 的值.
20. (本小题8分)如图,点A是反比例函数y=kx图象上的一点,过点A作AB⊥x轴于点B,连接OA,若△OAB的面积为2,求该反比例函数的解析式.
21. (本小题8分)已知:已知函数y = y1 +y2 , y1与x成正比例,y2与x成反比例,且当x = 1时,y =-1;当x = 3时,y = 5.求y关于x的函数关系式.
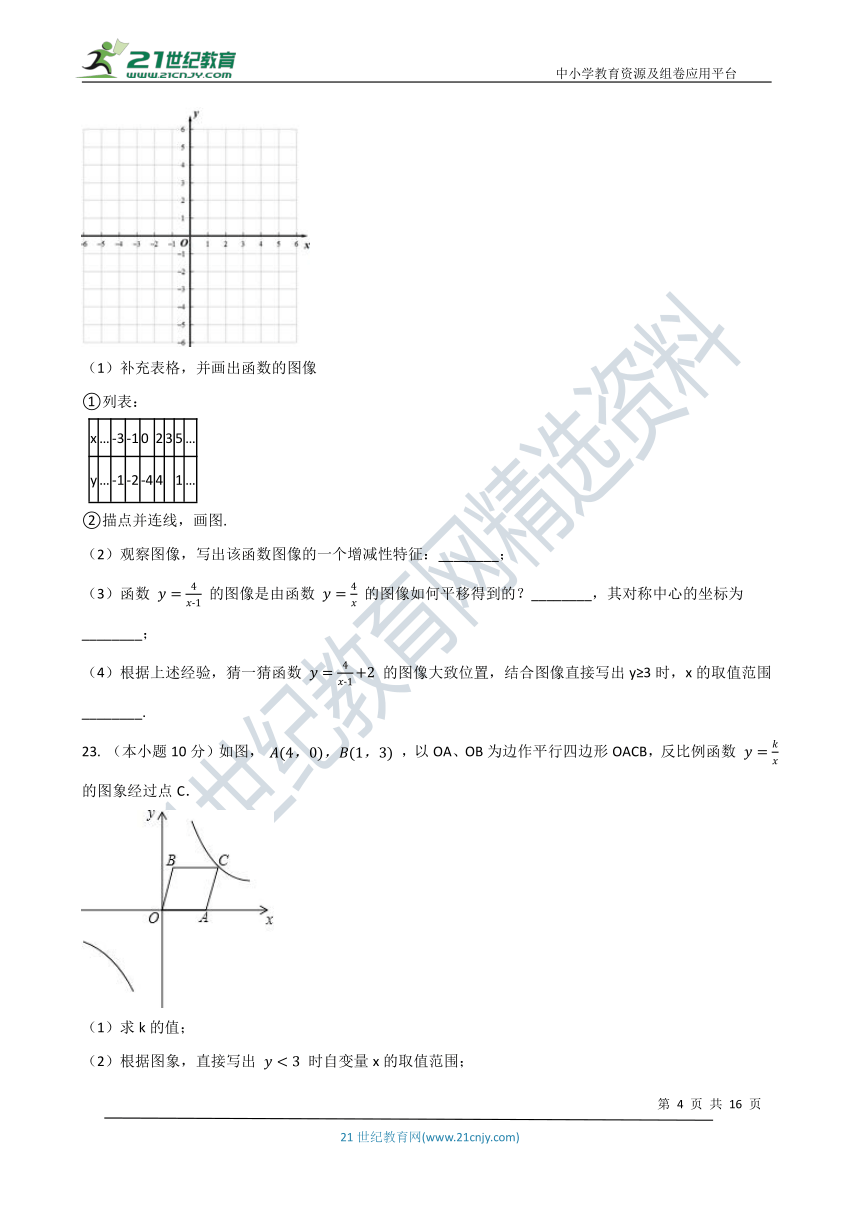
22. (本小题12分)在函数的学习中,我们经历了“确定函数表达式——画函数图像——利用函数图像研究函数性质——利用图像解决问题”的学习过程.我们可以借鉴这种方法探究函数 y=4x-1 的图像性质.
(1)补充表格,并画出函数的图像
①列表:
x
…
-3
-1
0
2
3
5
…
y
…
-1
-2
-4
4
1
…
②描点并连线,画图.
(2)观察图像,写出该函数图像的一个增减性特征:________;
(3)函数 y=4x-1 的图像是由函数 y=4x 的图像如何平移得到的?________,其对称中心的坐标为________;
(4)根据上述经验,猜一猜函数 y=4x-1+2 的图像大致位置,结合图像直接写出y≥3时,x的取值范围________.
23. (本小题10分)如图, A(4,0),B(1,3) ,以OA、OB为边作平行四边形OACB,反比例函数 y=kx 的图象经过点C.
(1)求k的值;
(2)根据图象,直接写出 y<3 时自变量x的取值范围;
(3)将平行四边形OACB向上平移几个单位长度,使点B落在反比例函数的图象上.
24. (本小题10分)某药品研究所研发一种抗菌新药,测得成人服用该药后血液中的药物浓度y(微克/毫升)与服药后时间x(小时)之间的函数关系如图所示,当血液中药物浓度上升 (0≤x≤a) 时,满足 y=2x ,下降时,y与x成反比例关系.
(1)求a的值,并求当 a≤x≤8 时,y与x的函数表达式;
(2)血液中药物浓度不低于3微克/毫升的持续时间是多少小时?
答案解析部分
一、单选题
1. C
考点:反比例函数的定义
解:反比例函数的定义是:“形如 y=kx (k≠0) 的函数叫做反比例函数”,其表达形式一般有3种,分别为:① y=kx (k≠0) ;② xy=k (k≠0) ;③ y=kx-1 (k≠0) ,上述四个选项中,只有C选项中的式子符合要求,故答案为:C.
分析:根据反比例函数的定义是:“形如 y=kx (k≠0) 的函数叫做反比例函数”和其表达形式"① y=kx (k≠0) ;② xy=k (k≠0) ;③ y=kx-1 (k≠0)"并结合各选项可判断求解.
2. D
考点:反比例函数的定义,正比例函数的定义
解:根据题意得P=I2R,
∵当P为定值时,
∴I2与R的乘积是定值,
所以I2与R成反比例.
故选:D.
分析:根据题意得到P=I2R,即I2和R的乘积为定值,所以根据反比例的概念应该是I2和R成反比例,而并非I与R成反比例.
3. B
考点:反比例函数的性质
解:∵C(3,﹣1)在反比例函数y= kx 的图象上
∴ k=3×(-1)=-3
∴函数的图象在二、四象限内,在每个象限内,y随x的增大而增大,
∵a>1,
∴0<a-1<a,
∴A、B两点均在第四象限,
∴m>n.
故答案为:B.
分析:本题考查反比例函数的性质,先 根据C(3,﹣1)在反比例函数y= kx ?的图象上. 求出k,再利用增减性即可求解.
4. B
考点:根据实际问题列反比例函数关系式
解:观察图象易知p与S之间的是反比例函数关系,设 P=kS ,
由于(16,10)在此函数解析式上,
∴k=16×10=160,
∴ P=200S ,
故答案为:B.
分析:观察图象可知p与S之间的是反比例函数关系,设P=ks , 把图中的点(20,10)代入解析式计算即可求解.
5. D
考点:反比例函数的定义
解:由反比例函数的概念可得:m(m-3)≠0,
解得m≠0且m≠3.
故答案为:D.
分析: 一般地,如果两个变量x、y之间的关系可以表示成y=kx (k为常数, k≠0)的形式,那么称y是x的反比例函数.
6. C
考点:反比例函数的图象,反比例函数的性质
解:①当 k>0 时, y=kx 的图象分布在第一、三象限,在每个象限内y随x的增大而减小,
∵ A(x1,-2) , C(x3,3)
∴点A在第三象限,点C在第一象限
∴ x1而已知条件中 x30 不存在;
当 k<0 时, y=kx 的图象分布在第二、四象限,在每个象限内y随x的增大而增大,
∵ A(x1,-2) , C(x3,3)
∴点A在第四象限,点C在第二象限
∴ x1>0 , x3<0
当 x33 ,当 0故 a 的取值范围为: a>3 或 a<-2 ,
故答案为:C.
分析:分两种情况:①当 k>0 时, y=kx 的图象分布在第一、三象限,在每个象限内y随x的增大而减小,从而得出点A在第三象限,点C在第一象限,②当 k<0 时, y=kx 的图象分布在第二、四象限,在每个象限内y随x的增大而增大,从而得出点A在第四象限,点C在第二象限,据此分别解答即可.
7. B
考点:一次函数图象与几何变换,反比例函数图象上点的坐标特征
解:∵将直线y=n向下平移4个单位长度后,
∴平移后直线的解析式为y=n﹣4,
∵ ABCD=13 ,
∴CD=3AB,
设B(a,n),D(3a,n﹣4),
∵B、D在反比例函数 y=kx(x>0) 的图象上,
∴an=3a?(n﹣4)
∴n=6
故答案为:B.
分析:设平移后直线的解析式为y=n﹣4,由ABCD=13 , 可设B(a,n),D(3a,n﹣4),利用反比例函数图象上点的坐标特征,得出an=3a?(n﹣4),求出a值即可.
8. B
考点:反比例函数的性质
解:∵反比例函数 y=m-2x (m为常数)的图象位于第一、三象限,
∴m﹣2>0,
解得:m>2.
故答案为:B.
分析:直接由反比例函数y=kx的图像和性质知k>0时图像位于一、三象限,令m-2>0,解出m即可.
9. B
考点:一次函数的图象,反比例函数的图象
解:若k>0,则 ?y=kx 位于一、三象限; ?y=-kx+1(k≠0) 经过一、二、四象限,结合选项可知B正确,D错误;
若k<0,则??y=kx 位于二、四象限; ?y=-kx+1(k≠0) 经过一、二、三象限,结合选项可知A、C错误.
故答案为:B.
分析:当k>0时,??y=kx 位于一、三象限; 当k<0时,y=kx位于二、四象限;当k>0时,?y=-kx+1(k≠0) 经过一、二、四象限;当k<0时,??y=-kx+1(k≠0) 经过一、二、三象限.
10. C
考点:反比例函数的图象,反比例函数图象的对称性,反比例函数的性质
解:∵k=-8<0,
∴函数图象分别位于第二、第四象限,故A不符合题意;
B、函数图象关于原点中心对称,故B不符合题意;
C、∵k<0,
∴在每一个象限y随x的增大而增大,故C符合题意;
D、当﹣8<x<﹣1时,﹣8<y<﹣1 ,故D不符合题意;
故答案为:C.
分析:由函数解析式可知k<0,可得到函数图象分别位于第二、第四象限,在每一个象限y随x的增大而增大,可对A,C作出判断;利用反比例函数的对称性,可对B作出判断;由x的取值范围可得到y的取值范围,可对D作出判断.
二、填空题
11. x≠1
考点:反比例函数的定义
解:∵y=1x-1 ,
∴x-1≠0,
解得:x≠1.
故答案为:x≠1.
分析:因为此函数是反比例函数,解析式为分式,根据分式有意义的条件,分母不为0,列出不等式,解不等式即可.
12. 18
考点:反比例函数的定义
解:∵y= 18x ﹣ 18x ,
∴反比例函数y= 18x 的比例系数是 18 ,
故答案为: 18 .
分析:将函数解析式变形为y= 18x ,依据反比例函数定义即可得出答案.
13. y=-1x (答案不唯一)
考点:反比例函数的性质
解:∵反比例函数的图象在每个象限内,y的值随x值的增大而增大,
∴k<0 ,
∴k可以取-1,
此时函数的解析式为 y=-1x ,
故答案为: y=-1x (答案不唯一).
分析:当k<0 , 反比例函数的图象在每个象限内,y的值随x值的增大而增大,据此解答即可(答案不唯一).
14. y= 100x
考点:根据实际问题列反比例函数关系式
解:设该反比例函数的解析式为 y=kx
将x= 0.25 ,y=400代入,得 400=k0.25
解得:k=100
∴眼镜度数与镜片焦距之间的函数关系式为 y=100x
故答案为: y=100x .
分析:设该反比例函数的解析式为 y=kx ,然后将x= 0.25 ,y=400代入即可求出函数关系式.
15. ﹣6
考点:反比例函数系数k的几何意义
解:依题可知 S△ABO=12|k|=3 ,
由于反比例函数的图象位于第二象限,即k<0,
则k=-6
故答案为:-6
分析:观察函数图象一个分支位于第二象限,可知k<0,再利用|k|=2S△AOB , 然后代入计算可求出k的值.
16. 2<k<6
考点:反比例函数与一次函数的交点问题
解:∵点A的横坐标为m,且满足2<m<3,
∴当x=2时,y2=1;当x=3时,y2=2;
∴A纵坐标y的取为1<y<2,
∵反比例函数y1= kx (k>0,x>0)的图象与直线y2=x﹣1在第一象限内的交点为A,
∴2<k<6,
所以k的取值范围为2<k<6,
故答案为:2<k<6.
分析:利用m的取值范围及点A的横坐标为m,可得到点A的纵坐标的取值范围,再根据两函数图像在第一象限的交点为点A,即可求出k的取值范围。
三、解答题
17. (1)解: ∵ x与y成反比例,
∴设y=kx,
于是k=xy,,
∴k=43×(-34),
∴k=-1
∴y=-1x
(2)解: 当x=-23?时 ,
y=-1-23=32.
考点:反比例函数的定义
分析:(1)设y=kx , 把 x=?-34?时,y=?43?代入函数式即可得k值。
(2)把 x=?-23?时代入求得的函数式,即可求出y的值.?
18. 解:由题意可知,m(m+1)=(m+3)(m﹣1).
解得m=3.
∴A(3,4),B(6,2),
∴k=4×3=12,
∴反比例函数的解析式为y= 12x .
考点:反比例函数图象上点的坐标特征
分析:根据反比例函数图象上各点的横纵坐标的积为定值求出m的值,再求出A点坐标,进而可得出k的值.
19. 解:根据题意,得 h=20a ( a>0 );
当 h=5 时, 5a=20 , a=4 .
考点:根据实际问题列反比例函数关系式
分析:根据平行四边形的面积公式,直接写出函数解析式即可,然后代入求值即可.
20. 解:∵△OAB的面积为2,
∴ 12 OB·AB=2,
即OB·AB=4.
∴|k︱=4.
∴k=±4.
∵y= kx 过一、三象限,
∴k>0,
∴k=4.
∴反比例函数解析式为 y=4x .
考点:反比例函数系数k的几何意义
分析:由题意根据反比例函数的k的几何意义得S△OAB=12k可求解.
21. 解:设y1=kx,y2= mx ,则y=kx+ mx ,
根据题意得 {k+m=-13k+m3=5 ,
解得 {k=2m=-3 ,
所以y与x之间的函数关系式为 y=2x-3x .
考点:函数解析式,反比例函数的定义,正比例函数的定义
分析:根据正比例函数和反比例函数的定义得到y1=kx,y2= mx ,则y=kx+ mx ,再利用当x=1时,y= -1,当x=3时,y=5得到关于k、m的方程组,然后解方程组求出k、m,即可得到y与x之间的函数关系式;
22. (1)解:补充表格,并画出函数的图像
①列表:
x
…
-3
-1
0
2
3
5
…
y
…
-1
-2
-4
4
2
1
…
②描点并连线,画图.
(2)当x>1时,y随着x的增大减小
(3)函数y= 4x-1 的图象是由函数y= 4x 的图象向右平移1个单位;(1,0)
(4)1考点:反比例函数的图象,反比例函数的性质
解:(2)观察图象,当x>1时,y随着x的增大减小.
故答案为:当x>1时,y随着x的增大减小;
( 3 )由函数的平移规律,得函数y= 4x 的图象向右平移1个单位,自变量
x变为x-1,函数的解析式变为y= 4x-1 ,其函数y= 4x 的对称中心的坐标由(0,0)变为(1,0).
故答案为:函数y= 4x-1 的图象是由函数y= 4x 的图象向右平移1个单位;(1,0).
( 4 )根据函数图像的平移规律画出图像,结合图像可知:当1故答案为:1分析:(1)将x=3代入解析式即可得y的值,再画出函数的图象;(2)结合图象,可从函数的增减性方面写出一条即可;(3)根据函数图像的平移规律:“左加,右减”即可得到答案;(4)根据函数图像的平移规律:“左加,右减;上加,下减”可到函数图像的位置,结合图像即可得到答案;
23. (1)解: ∵ 平行四边形OACB中, A(4,0),B(1,3) ,
∴C(5,3) ,
把 C(5,3) 代入 y=kx ,得: 3=k5 ,
解得: k=15
(2)解: y<3 时自变量x的取值范围为: x>5 或 x<0
(3)解:把 x=1 代入 y=15x ,
解得: y=15 ,
∴ 向上平移 15-3=12 个单位
考点:坐标与图形性质,待定系数法求反比例函数解析式,平行四边形的性质
分析:(1)根据平行四边形的性质及A、B的坐标,可得C ( 5 , 3 ),再根据反比例函数图像点的坐标特征,求出k值;
(2)观察图像,直接得出 y < 3 时自变量x的取值范围: x > 5 或 x < 0
(3)由反比例函数图像点的坐标特征知当x=1时,Y=15,由平移的性质及B(1,3)可得出结果;
24. (1)解:将 y=6 代入 y=2x 中,得 2x=6 ,解得 x=3 ,∴ a=3 .
又由题意可知;当 3≤x≤8 时,y与x成反比,设 y=mx .
由图象可知,当 x=3 时, y=6 ,
∴ m=3×6=18 ,
∴当 3≤x≤8 时,y与x的函数表达式为 y=18x(3≤x≤8) .
(2)解:把 y=3 代入 y=2x 中,得 2x=3 ,解得 x=1.5 ,
把 y=3 代入 y=18x 中,得 18x=3 ,解得 x=6 ,
∵ 6-1.5=4.5 ,
∴血液中药物浓度不低于3微克/毫升的持续时间是4.5小时.
考点:反比例函数与一次函数的交点问题
分析:(1)把y=6代入y=2x得到x的值,进而得到a的值,再把(3,6)代入 ,得到m的值,进而得到函数解析式.
(2)把y=3分别代入y=2x和 ,得到x的值,进而得到持续的时间.
一、单选题(本大题共10小题,每小题3分,共30分。)
1.在下列函数中,y是x的反比例函数的是( )
A.?y=x-1?????????????????????????????B.?y= 8x2?????????????????????????????C.?y=-2x-1?????????????????????????????D.?yx =2
2.已知某用电器的输出功率为P、电阻为R,通过的电流为I,当P为定值时,下面说法正确的是(??? )
A.?I 是 R 的正比例函数??????????????????????????????????????????B.?I2 是 R 的正比例函数
C.?I 是 R 的反比例函数??????????????????????????????????????????D.?I2 是 R 的反比例函数
3.已知点A(a,m),B(a﹣1,n),C(3,﹣1)在反比例函数y= kx ?的图象上.若a>1,则m,n的大小关系是(?? )
A.?m<n???????????????????????????B.?m>n???????????????????????????C.?m=n???????????????????????????D.?m,n的大小不确定
4.某物体对地面的压力为定值,物体对地面的压强 P(Pa) 与受力面积 S(m2) 之间的函数关系如图所示,这一函数表达式为(?? )
A.?P=20S?????????????????????????????B.?P=200S?????????????????????????????C.?S=20P?????????????????????????????D.?S=200P
5.若 y=m(m-3)x 是反比例函数,则m满足的条件是(?? )
??A.?m≠0????????????????????????????B.?m=3????????????????????????????C.?m=3或m=0????????????????????????????D.?m≠3且m≠0
6.在已知反比例函数 y=kx (k为常数)的图象上有三点 A(x1,-2) , B(x2,a) , C(x3,3) ,若 x3
?
A.?4???????????????????????????????????????????B.?6???????????????????????????????????????????C.?2???????????????????????????????????????????D.?5
8.反比例函数 y=m-2x ( m 为常数)的图象位于第一、三象限,则m的取值范围是( )
A.?m>0??????????????????????????????????B.?m>2??????????????????????????????????C.?m<0??????????????????????????????????D.?m<2
9.如图,函数 y=kx 与 y=-kx+1(k≠0) 在同一平面直角坐标系中的大致图象是(?? )
A.??????????????????B.??????????????????C.??????????????????D.?
10.关于反比例函数y= 8x ,下列说法不正确的是(?? )
A.?函数图象分别位于第一、第三象限??????????????????????B.?函数图象关于原点中心对称
C.?当x>0时,y随x的增大而增大?????????????????????????????D.?当﹣8<x<﹣1时,﹣8<y<﹣1
二、填空题(本大题共6小题,每小题4分,共24分。)
11.函数y= 1x-1 的自变量x的取值范围是________?。
12.反比例函数y= 18x 的比例系数为________.
13.写出一个反比例函数y= kx (k≠0),使它的图象在每个象限内,y的值随x值的增大而增大,这个函数的解析式为________.
14.近视眼镜的度数y(度)与镜片焦距x(m)成反比例,已知400度近视眼镜镜片的焦距为0.25m,则眼镜度数与镜片焦距之间的函数关系式为________.
15.如图,点A是反比例函数y= kx (k≠0)图象上第二象限内的一点,若△ABO的面积为3,则k的值为________
16.若反比例函数y1= kx (k>0,x>0)的图象与直线y2=x﹣1在第一象限内的交点为A,点A的横坐标为m,且满足2<m<3,则k的取值范围是________.
三、解答题(本大题共8小题,共66分。)
17. (本小题6分)已知x与y成反比例,且当x= -34 时,y= 43
(1)求y关于x的函数表达式
(2)当x= -23 时,y的值是多少?
18. (本小题6分)已知点A(m,m+1),B(m+3,m﹣1)都在反比例函数y= kx 的图象上,求m的值及反比例函数的解析式.
19. (本小题6分)设面积为 20cm2 的平行四边形的一边长为 a cm ,这条边上的高为 h cm .求 h 关于 a 的函数解析式(写出自变量 a 的取值范围)并求当 h=5 时, a 的值.
20. (本小题8分)如图,点A是反比例函数y=kx图象上的一点,过点A作AB⊥x轴于点B,连接OA,若△OAB的面积为2,求该反比例函数的解析式.
21. (本小题8分)已知:已知函数y = y1 +y2 , y1与x成正比例,y2与x成反比例,且当x = 1时,y =-1;当x = 3时,y = 5.求y关于x的函数关系式.
22. (本小题12分)在函数的学习中,我们经历了“确定函数表达式——画函数图像——利用函数图像研究函数性质——利用图像解决问题”的学习过程.我们可以借鉴这种方法探究函数 y=4x-1 的图像性质.
(1)补充表格,并画出函数的图像
①列表:
x
…
-3
-1
0
2
3
5
…
y
…
-1
-2
-4
4
1
…
②描点并连线,画图.
(2)观察图像,写出该函数图像的一个增减性特征:________;
(3)函数 y=4x-1 的图像是由函数 y=4x 的图像如何平移得到的?________,其对称中心的坐标为________;
(4)根据上述经验,猜一猜函数 y=4x-1+2 的图像大致位置,结合图像直接写出y≥3时,x的取值范围________.
23. (本小题10分)如图, A(4,0),B(1,3) ,以OA、OB为边作平行四边形OACB,反比例函数 y=kx 的图象经过点C.
(1)求k的值;
(2)根据图象,直接写出 y<3 时自变量x的取值范围;
(3)将平行四边形OACB向上平移几个单位长度,使点B落在反比例函数的图象上.
24. (本小题10分)某药品研究所研发一种抗菌新药,测得成人服用该药后血液中的药物浓度y(微克/毫升)与服药后时间x(小时)之间的函数关系如图所示,当血液中药物浓度上升 (0≤x≤a) 时,满足 y=2x ,下降时,y与x成反比例关系.
(1)求a的值,并求当 a≤x≤8 时,y与x的函数表达式;
(2)血液中药物浓度不低于3微克/毫升的持续时间是多少小时?
答案解析部分
一、单选题
1. C
考点:反比例函数的定义
解:反比例函数的定义是:“形如 y=kx (k≠0) 的函数叫做反比例函数”,其表达形式一般有3种,分别为:① y=kx (k≠0) ;② xy=k (k≠0) ;③ y=kx-1 (k≠0) ,上述四个选项中,只有C选项中的式子符合要求,故答案为:C.
分析:根据反比例函数的定义是:“形如 y=kx (k≠0) 的函数叫做反比例函数”和其表达形式"① y=kx (k≠0) ;② xy=k (k≠0) ;③ y=kx-1 (k≠0)"并结合各选项可判断求解.
2. D
考点:反比例函数的定义,正比例函数的定义
解:根据题意得P=I2R,
∵当P为定值时,
∴I2与R的乘积是定值,
所以I2与R成反比例.
故选:D.
分析:根据题意得到P=I2R,即I2和R的乘积为定值,所以根据反比例的概念应该是I2和R成反比例,而并非I与R成反比例.
3. B
考点:反比例函数的性质
解:∵C(3,﹣1)在反比例函数y= kx 的图象上
∴ k=3×(-1)=-3
∴函数的图象在二、四象限内,在每个象限内,y随x的增大而增大,
∵a>1,
∴0<a-1<a,
∴A、B两点均在第四象限,
∴m>n.
故答案为:B.
分析:本题考查反比例函数的性质,先 根据C(3,﹣1)在反比例函数y= kx ?的图象上. 求出k,再利用增减性即可求解.
4. B
考点:根据实际问题列反比例函数关系式
解:观察图象易知p与S之间的是反比例函数关系,设 P=kS ,
由于(16,10)在此函数解析式上,
∴k=16×10=160,
∴ P=200S ,
故答案为:B.
分析:观察图象可知p与S之间的是反比例函数关系,设P=ks , 把图中的点(20,10)代入解析式计算即可求解.
5. D
考点:反比例函数的定义
解:由反比例函数的概念可得:m(m-3)≠0,
解得m≠0且m≠3.
故答案为:D.
分析: 一般地,如果两个变量x、y之间的关系可以表示成y=kx (k为常数, k≠0)的形式,那么称y是x的反比例函数.
6. C
考点:反比例函数的图象,反比例函数的性质
解:①当 k>0 时, y=kx 的图象分布在第一、三象限,在每个象限内y随x的增大而减小,
∵ A(x1,-2) , C(x3,3)
∴点A在第三象限,点C在第一象限
∴ x1
当 k<0 时, y=kx 的图象分布在第二、四象限,在每个象限内y随x的增大而增大,
∵ A(x1,-2) , C(x3,3)
∴点A在第四象限,点C在第二象限
∴ x1>0 , x3<0
当 x3
故答案为:C.
分析:分两种情况:①当 k>0 时, y=kx 的图象分布在第一、三象限,在每个象限内y随x的增大而减小,从而得出点A在第三象限,点C在第一象限,②当 k<0 时, y=kx 的图象分布在第二、四象限,在每个象限内y随x的增大而增大,从而得出点A在第四象限,点C在第二象限,据此分别解答即可.
7. B
考点:一次函数图象与几何变换,反比例函数图象上点的坐标特征
解:∵将直线y=n向下平移4个单位长度后,
∴平移后直线的解析式为y=n﹣4,
∵ ABCD=13 ,
∴CD=3AB,
设B(a,n),D(3a,n﹣4),
∵B、D在反比例函数 y=kx(x>0) 的图象上,
∴an=3a?(n﹣4)
∴n=6
故答案为:B.
分析:设平移后直线的解析式为y=n﹣4,由ABCD=13 , 可设B(a,n),D(3a,n﹣4),利用反比例函数图象上点的坐标特征,得出an=3a?(n﹣4),求出a值即可.
8. B
考点:反比例函数的性质
解:∵反比例函数 y=m-2x (m为常数)的图象位于第一、三象限,
∴m﹣2>0,
解得:m>2.
故答案为:B.
分析:直接由反比例函数y=kx的图像和性质知k>0时图像位于一、三象限,令m-2>0,解出m即可.
9. B
考点:一次函数的图象,反比例函数的图象
解:若k>0,则 ?y=kx 位于一、三象限; ?y=-kx+1(k≠0) 经过一、二、四象限,结合选项可知B正确,D错误;
若k<0,则??y=kx 位于二、四象限; ?y=-kx+1(k≠0) 经过一、二、三象限,结合选项可知A、C错误.
故答案为:B.
分析:当k>0时,??y=kx 位于一、三象限; 当k<0时,y=kx位于二、四象限;当k>0时,?y=-kx+1(k≠0) 经过一、二、四象限;当k<0时,??y=-kx+1(k≠0) 经过一、二、三象限.
10. C
考点:反比例函数的图象,反比例函数图象的对称性,反比例函数的性质
解:∵k=-8<0,
∴函数图象分别位于第二、第四象限,故A不符合题意;
B、函数图象关于原点中心对称,故B不符合题意;
C、∵k<0,
∴在每一个象限y随x的增大而增大,故C符合题意;
D、当﹣8<x<﹣1时,﹣8<y<﹣1 ,故D不符合题意;
故答案为:C.
分析:由函数解析式可知k<0,可得到函数图象分别位于第二、第四象限,在每一个象限y随x的增大而增大,可对A,C作出判断;利用反比例函数的对称性,可对B作出判断;由x的取值范围可得到y的取值范围,可对D作出判断.
二、填空题
11. x≠1
考点:反比例函数的定义
解:∵y=1x-1 ,
∴x-1≠0,
解得:x≠1.
故答案为:x≠1.
分析:因为此函数是反比例函数,解析式为分式,根据分式有意义的条件,分母不为0,列出不等式,解不等式即可.
12. 18
考点:反比例函数的定义
解:∵y= 18x ﹣ 18x ,
∴反比例函数y= 18x 的比例系数是 18 ,
故答案为: 18 .
分析:将函数解析式变形为y= 18x ,依据反比例函数定义即可得出答案.
13. y=-1x (答案不唯一)
考点:反比例函数的性质
解:∵反比例函数的图象在每个象限内,y的值随x值的增大而增大,
∴k<0 ,
∴k可以取-1,
此时函数的解析式为 y=-1x ,
故答案为: y=-1x (答案不唯一).
分析:当k<0 , 反比例函数的图象在每个象限内,y的值随x值的增大而增大,据此解答即可(答案不唯一).
14. y= 100x
考点:根据实际问题列反比例函数关系式
解:设该反比例函数的解析式为 y=kx
将x= 0.25 ,y=400代入,得 400=k0.25
解得:k=100
∴眼镜度数与镜片焦距之间的函数关系式为 y=100x
故答案为: y=100x .
分析:设该反比例函数的解析式为 y=kx ,然后将x= 0.25 ,y=400代入即可求出函数关系式.
15. ﹣6
考点:反比例函数系数k的几何意义
解:依题可知 S△ABO=12|k|=3 ,
由于反比例函数的图象位于第二象限,即k<0,
则k=-6
故答案为:-6
分析:观察函数图象一个分支位于第二象限,可知k<0,再利用|k|=2S△AOB , 然后代入计算可求出k的值.
16. 2<k<6
考点:反比例函数与一次函数的交点问题
解:∵点A的横坐标为m,且满足2<m<3,
∴当x=2时,y2=1;当x=3时,y2=2;
∴A纵坐标y的取为1<y<2,
∵反比例函数y1= kx (k>0,x>0)的图象与直线y2=x﹣1在第一象限内的交点为A,
∴2<k<6,
所以k的取值范围为2<k<6,
故答案为:2<k<6.
分析:利用m的取值范围及点A的横坐标为m,可得到点A的纵坐标的取值范围,再根据两函数图像在第一象限的交点为点A,即可求出k的取值范围。
三、解答题
17. (1)解: ∵ x与y成反比例,
∴设y=kx,
于是k=xy,,
∴k=43×(-34),
∴k=-1
∴y=-1x
(2)解: 当x=-23?时 ,
y=-1-23=32.
考点:反比例函数的定义
分析:(1)设y=kx , 把 x=?-34?时,y=?43?代入函数式即可得k值。
(2)把 x=?-23?时代入求得的函数式,即可求出y的值.?
18. 解:由题意可知,m(m+1)=(m+3)(m﹣1).
解得m=3.
∴A(3,4),B(6,2),
∴k=4×3=12,
∴反比例函数的解析式为y= 12x .
考点:反比例函数图象上点的坐标特征
分析:根据反比例函数图象上各点的横纵坐标的积为定值求出m的值,再求出A点坐标,进而可得出k的值.
19. 解:根据题意,得 h=20a ( a>0 );
当 h=5 时, 5a=20 , a=4 .
考点:根据实际问题列反比例函数关系式
分析:根据平行四边形的面积公式,直接写出函数解析式即可,然后代入求值即可.
20. 解:∵△OAB的面积为2,
∴ 12 OB·AB=2,
即OB·AB=4.
∴|k︱=4.
∴k=±4.
∵y= kx 过一、三象限,
∴k>0,
∴k=4.
∴反比例函数解析式为 y=4x .
考点:反比例函数系数k的几何意义
分析:由题意根据反比例函数的k的几何意义得S△OAB=12k可求解.
21. 解:设y1=kx,y2= mx ,则y=kx+ mx ,
根据题意得 {k+m=-13k+m3=5 ,
解得 {k=2m=-3 ,
所以y与x之间的函数关系式为 y=2x-3x .
考点:函数解析式,反比例函数的定义,正比例函数的定义
分析:根据正比例函数和反比例函数的定义得到y1=kx,y2= mx ,则y=kx+ mx ,再利用当x=1时,y= -1,当x=3时,y=5得到关于k、m的方程组,然后解方程组求出k、m,即可得到y与x之间的函数关系式;
22. (1)解:补充表格,并画出函数的图像
①列表:
x
…
-3
-1
0
2
3
5
…
y
…
-1
-2
-4
4
2
1
…
②描点并连线,画图.
(2)当x>1时,y随着x的增大减小
(3)函数y= 4x-1 的图象是由函数y= 4x 的图象向右平移1个单位;(1,0)
(4)1
解:(2)观察图象,当x>1时,y随着x的增大减小.
故答案为:当x>1时,y随着x的增大减小;
( 3 )由函数的平移规律,得函数y= 4x 的图象向右平移1个单位,自变量
x变为x-1,函数的解析式变为y= 4x-1 ,其函数y= 4x 的对称中心的坐标由(0,0)变为(1,0).
故答案为:函数y= 4x-1 的图象是由函数y= 4x 的图象向右平移1个单位;(1,0).
( 4 )根据函数图像的平移规律画出图像,结合图像可知:当1
23. (1)解: ∵ 平行四边形OACB中, A(4,0),B(1,3) ,
∴C(5,3) ,
把 C(5,3) 代入 y=kx ,得: 3=k5 ,
解得: k=15
(2)解: y<3 时自变量x的取值范围为: x>5 或 x<0
(3)解:把 x=1 代入 y=15x ,
解得: y=15 ,
∴ 向上平移 15-3=12 个单位
考点:坐标与图形性质,待定系数法求反比例函数解析式,平行四边形的性质
分析:(1)根据平行四边形的性质及A、B的坐标,可得C ( 5 , 3 ),再根据反比例函数图像点的坐标特征,求出k值;
(2)观察图像,直接得出 y < 3 时自变量x的取值范围: x > 5 或 x < 0
(3)由反比例函数图像点的坐标特征知当x=1时,Y=15,由平移的性质及B(1,3)可得出结果;
24. (1)解:将 y=6 代入 y=2x 中,得 2x=6 ,解得 x=3 ,∴ a=3 .
又由题意可知;当 3≤x≤8 时,y与x成反比,设 y=mx .
由图象可知,当 x=3 时, y=6 ,
∴ m=3×6=18 ,
∴当 3≤x≤8 时,y与x的函数表达式为 y=18x(3≤x≤8) .
(2)解:把 y=3 代入 y=2x 中,得 2x=3 ,解得 x=1.5 ,
把 y=3 代入 y=18x 中,得 18x=3 ,解得 x=6 ,
∵ 6-1.5=4.5 ,
∴血液中药物浓度不低于3微克/毫升的持续时间是4.5小时.
考点:反比例函数与一次函数的交点问题
分析:(1)把y=6代入y=2x得到x的值,进而得到a的值,再把(3,6)代入 ,得到m的值,进而得到函数解析式.
(2)把y=3分别代入y=2x和 ,得到x的值,进而得到持续的时间.
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
