4.3中心对称图形-2020-2021学年浙教版八年级数学下册同步提升训练(含答案)
文档属性
| 名称 | 4.3中心对称图形-2020-2021学年浙教版八年级数学下册同步提升训练(含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 406.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-09 23:50:39 | ||
图片预览


文档简介
2020-2021年度浙教版八年级数学下册《4.3中心对称图形》同步提升训练(附答案)
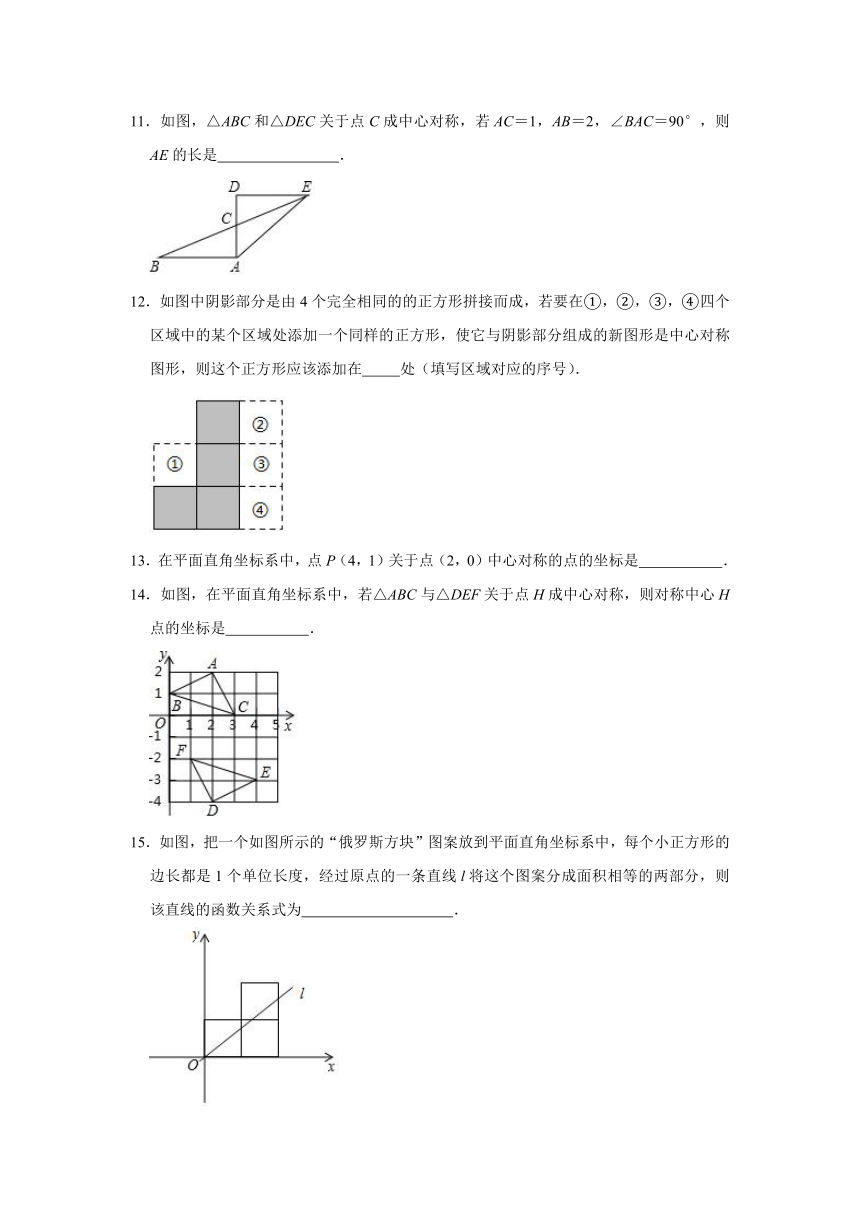
1.下列图形中,可以看作既是轴对称图形又是中心对称图形的是( )
A.B.C.D.
2.下列图形中,既是轴对称图形又是中心对称图形的是( )
A.角 B.等腰三角形 C.平行四边形 D.正六边形
3.下列图形中,可以看作是中心对称图形的是( )
A. B. C. D.
4.已知点A(2,7),B(﹣5,0),C(0,﹣1),在平面直角坐标系中△A'B'C'以点P(5,6)为对称中心与△ABC成中心对称,则点A'的坐标为( )
A.(﹣2,﹣7) B.(7,2) C.(8,8) D.(8,5)
5.平面直角坐标系中,△OA1B1是边长为2的等边三角形,作△B2A2B1与△OA1B1关于点B1成中心对称,再作△B2A3B3与△B2A2B1关于点B2成中心对称,如此作下去,则△B2020A2021B2021(n是正整数)的顶点A2021的坐标是( )
A.(4041,) B.(4041,﹣) C.(4043,) D.(4043,﹣)
6.把四张扑克牌所摆放的顺序与位置如下,小杨同学选取其中一张扑克牌把他颠倒后再放回原来的位置,那么扑克牌的摆放顺序与位置都没变化,那么小杨同学所选的扑克牌是( )
A. B. C. D.
7.点O是平行四边形ABCD的对称中心,AD>AB,E、F分别是AB边上的点,且EF=AB;G、H分别是BC边上的点,且GH=BC;若S1,S2分别表示△EOF和△GOH的面积,则S1,S2之间的等量关系是S1= S2.
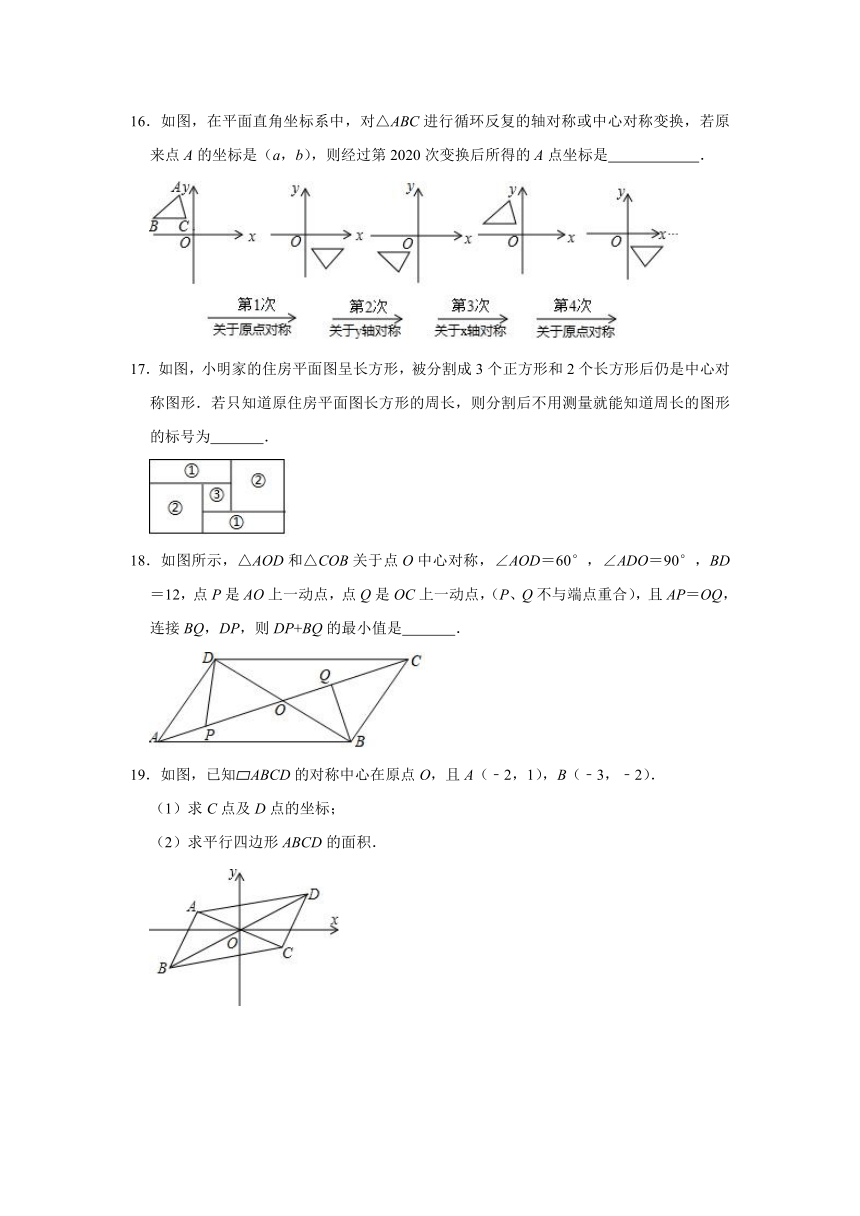
8.如图,三个边长均为2的正方形重叠在一起,O1,O2是其中两个正方形的对角线交点,若把这样的n个小正方形按如图所示方式摆放,则重叠部分的面积为 .
9.如图,将△ABC绕点C(0,﹣1)旋转180°得到△A′B′C,若点A的坐标为(﹣4,﹣3),则点A′的坐标为 .
10.如图,在平面直角坐标系中将△ABC向右平移3个单位长度后得到△A1B1C1,再将△A1B1C1绕点O旋转180°后得到△A2B2C2,则B2C的长度是 .
11.如图,△ABC和△DEC关于点C成中心对称,若AC=1,AB=2,∠BAC=90°,则AE的长是 .
12.如图中阴影部分是由4个完全相同的的正方形拼接而成,若要在①,②,③,④四个区域中的某个区域处添加一个同样的正方形,使它与阴影部分组成的新图形是中心对称图形,则这个正方形应该添加在 处(填写区域对应的序号).
13.在平面直角坐标系中,点P(4,1)关于点(2,0)中心对称的点的坐标是 .
14.如图,在平面直角坐标系中,若△ABC与△DEF关于点H成中心对称,则对称中心H点的坐标是 .
15.如图,把一个如图所示的“俄罗斯方块”图案放到平面直角坐标系中,每个小正方形的边长都是1个单位长度,经过原点的一条直线l将这个图案分成面积相等的两部分,则该直线的函数关系式为 .
16.如图,在平面直角坐标系中,对△ABC进行循环反复的轴对称或中心对称变换,若原来点A的坐标是(a,b),则经过第2020次变换后所得的A点坐标是 .
17.如图,小明家的住房平面图呈长方形,被分割成3个正方形和2个长方形后仍是中心对称图形.若只知道原住房平面图长方形的周长,则分割后不用测量就能知道周长的图形的标号为 .
18.如图所示,△AOD和△COB关于点O中心对称,∠AOD=60°,∠ADO=90°,BD=12,点P是AO上一动点,点Q是OC上一动点,(P、Q不与端点重合),且AP=OQ,连接BQ,DP,则DP+BQ的最小值是 .
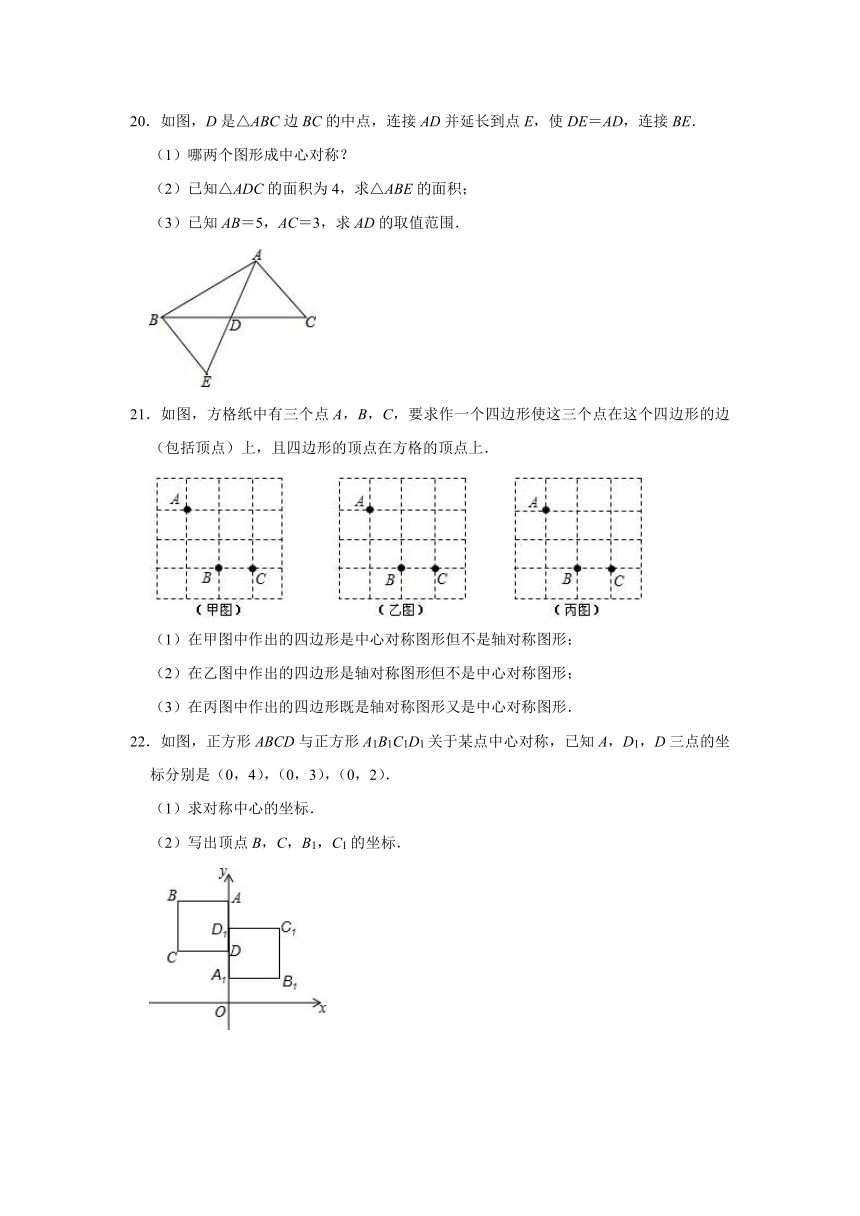
19.如图,已知?ABCD的对称中心在原点O,且A(﹣2,1),B(﹣3,﹣2).
(1)求C点及D点的坐标;
(2)求平行四边形ABCD的面积.
20.如图,D是△ABC边BC的中点,连接AD并延长到点E,使DE=AD,连接BE.
(1)哪两个图形成中心对称?
(2)已知△ADC的面积为4,求△ABE的面积;
(3)已知AB=5,AC=3,求AD的取值范围.
21.如图,方格纸中有三个点A,B,C,要求作一个四边形使这三个点在这个四边形的边(包括顶点)上,且四边形的顶点在方格的顶点上.
(1)在甲图中作出的四边形是中心对称图形但不是轴对称图形;
(2)在乙图中作出的四边形是轴对称图形但不是中心对称图形;
(3)在丙图中作出的四边形既是轴对称图形又是中心对称图形.
22.如图,正方形ABCD与正方形A1B1C1D1关于某点中心对称,已知A,D1,D三点的坐标分别是(0,4),(0,3),(0,2).
(1)求对称中心的坐标.
(2)写出顶点B,C,B1,C1的坐标.
23.已知:如图,三角形ABM与三角形ACM关于直线AF成轴对称,三角形ABE与三角形DCE关于点E成中心对称,点E、D、M都在线段AF上,BM的延长线交CF于点P.
(1)求证:AC=CD;
(2)若∠BAC=2∠MPC,请你判断∠F与∠MCD的数量关系,并说明理由.
24.如图所示,已知?OABC,其中点O,A,B,C的坐标分别为O(0,0),A(3,a),B(4,0),C(b,﹣1),求:
(1)?OABC的对称中心的坐标.
(2)a+b的值.
25.四边形ABCD是以点O为对称中心的中心对称图形,过点O作OE⊥AC交BC于点E,如果△ABE的周长为24cm,求四边形ABCD的周长.
26.如图,已知四边形ABCD是中心对称图形,E、F是对角线BD上的两点,且DE=BF,求证:
(1)△ADE≌△CBF;
(2)AE∥CF.
参考答案
1.解:A、不是轴对称图形,是中心对称图形,故本选项不合题意;
B、不是轴对称图形,是中心对称图形,故本选项不合题意;
C、是轴对称图形,不是中心对称图形,故本选项不合题意;
D、既是轴对称图形,又是中心对称图形,故本选项符合题意.
故选:D.
2.解:A.角是轴对称图形,不是中心对称图形,故本选项不符合题意;
B.等腰三角形是轴对称图形,不是中心对称图形,故本选项不符合题意;
C.平行四边形不是轴对称图形,是中心对称图形,故本选项不符合题意;
D.正六边形既是轴对称图形又是中心对称图形,故本选项符合题意.
故选:D.
3.解:A.旋转180°,与原图形能够完全重合是中心对称图形;故此选项符合题意;
B.旋转180°,不能与原图形能够完全重合不是中心对称图形;故此选项不合题意;
C.旋转180°,不能与原图形能够完全重合不是中心对称图形;故此选项不合题意;
D.旋转180°,不能与原图形能够完全重合不是中心对称图形;故此选项不合题意;
故选:A.
4.解:设A′(m,n),
由题意,A(2,7),A′(m,n)关于P(5,6)对称,
∴5=,6=,
∴m=8,n=5,
∴A′(8,5),
故选:D.
5.解:∵△OA1B1是边长为2的等边三角形,
∴A1的坐标为:(1,),B1的坐标为:(2,0),
∵△B2A2B1与△OA1B1关于点B1成中心对称,
∴点A2与点A1关于点B1成中心对称,
∵2×2﹣1=3,2×0﹣=﹣,
∴点A2的坐标是:(3,﹣),
∵△B2A3B3与△B2A2B1关于点B2成中心对称,
∴点A3与点A2关于点B2成中心对称,
∵2×4﹣3=5,2×0﹣(﹣)=,
∴点A3的坐标是:(5,),
∵△B3A4B4与△B3A3B2关于点B3成中心对称,
∴点A4与点A3关于点B3成中心对称,
∵2×6﹣5=7,2×0﹣=﹣,
∴点A4的坐标是:(7,﹣),…,
∵1=2×1﹣1,3=2×2﹣1,5=2×3﹣1,7=2×4﹣1,…,
∴An的横坐标是:2n﹣1,A2n+1的横坐标是:2(2n+1)﹣1=4n+1,
∵当n为奇数时,An的纵坐标是:,当n为偶数时,An的纵坐标是:﹣,
∴顶点A2n+1的纵坐标是:,
∴△B2nA2n+1B2n+1(n是正整数)的顶点A2n+1的坐标是:(4n+1,),
∴△B2020A2021B2021的顶点A2021的横坐标是:4×1010+1=4041,纵坐标是:,
故选:A.
6.解:四张扑克牌:“黑桃7,黑桃8,黑桃9,黑桃10”中,只有黑桃10是中心对称图形,其余的都不是.
故选:D.
7.解:如图,连接OA,OB,OC.设平行四边形的面积为4s.
∵点O是平行四边形ABCD的对称中心,
∴S△AOB=S△BOC=S平行四边形ABCD=s,
∵EF=AB,GH=BC,
∴S1=s,S2=s,
∴==,
故答案为:.
8.解:连接O1B、O1C,如图:
∵∠BO1F+∠FO1C=90°,∠FO1C+∠CO1G=90°,
∴∠BO1F=∠CO1G,
∵四边形ABCD是正方形,
∴∠O1BF=∠O1CG=45°,
在△O1BF和△O1CG中,
,
∴△O1BF≌△O1CG(ASA),
∴O1、O2两个正方形阴影部分的面积是S正方形=1,
同理另外两个正方形阴影部分的面积也是S正方形=1,
∴把这样的n个小正方形按如图所示方式摆放,则重叠部分的面积为(n﹣1).
故答案为:n﹣1
9.解:作A′E⊥y轴于点E,AD⊥y轴于点D,则∠A′EC=∠ADC,
∵∠A′CE=∠ACD,AC=A′C,
∴△A′EC≌△ADC(AAS),
∴AD=A′E=4,CE=CD,
∵OD=3,OC=1,
∴CD=2,
∴CE=2,
∴OE=1,
∴点A′的坐标为(4,1).
故答案为:(4,1).
10.解:如图所示:B2C的长度是:=.
故答案为:.
11.解:∵△DEC与△ABC关于点C成中心对称,
∴△ABC≌△DEC,
∴AB=DE=2,AC=DC=1,∠D=∠BAC=90°,
∴AD=2,
∵∠D=90°,
∴AE==2,
故答案为2.
12.解:把正方形添加在②处,使它与阴影部分组成的新图形是中心对称图形,
故答案为:②.
13.解:如图所示:点P(4,1)关于点(2,0)中心对称的点的坐标是:(0,﹣1).
故答案为:(0,﹣1).
14.解:如图,连接AD、CF,则交点就是对称中心H点.
观察图形可知,H(2,﹣1).
故答案为:(2,﹣1).
15.解:设直线l与俄罗斯方块交于点A.
∵直线l将这个图案分成面积相等的两部分,
∴S△OAB==,
即=,
×2×AB=,
AB=,
∴A(2,),
设直线l解析式y=kx,
将A(2,)代入,得=2k,
解得k=,
∴该直线的函数关系式为y=x,
故答案为y=x.
16.解:点A第一次关于原点对称后在第四象限,
点A第二次关于x轴后在第三象限,
点A第三次关于y轴对称后在第二象限,即点A回到原始位置,
所以,每3次对称为一个循环组依次循环,
∵用2020÷3=673余1,
∴经过第2020次变换后所得的A点与第四次变换的位置相同,在第四象限,坐标为(﹣a,﹣b).
故答案为:(﹣a,﹣b).
17.解:如图1:
设图形①的长和宽分别是a、c,图形②的边长是b,图形③的边长是d,原来大长方形的周长是l,
则l=2(a+2b+c),
根据图示,可得,
①﹣②,可得:a﹣b=b﹣c,
∴2b=a+c,
∴l=2(a+2b+c)=2×2(a+c)=4(a+c),或l=2(a+2b+c)=2×4b=8b,
∴2(a+c)=,4b=,
∵图形①的周长是2(a+c),图形②的周长是4b,的值一定,
∴图形①②的周长是定值,不用测量就能知道,图形③的周长不用测量无法知道.
∴分割后不用测量就能知道周长的图形的标号为①②.
故答案为:①②.
18.解:DP+BQ最小值是12;理由如下:
当AP=OP时,DP+BQ的值最小,此时P为OA的中点,
∵∠ADO=90°,
∴DP=OA=6,
同理BQ=6,
∴DP+BQ的最小值=6+6=12,
故答案为:12
19.解:(1)∵四边形ABCD是平行四边形,
∴四边形ABCD关于O中心对称,
∵A(﹣2,1),B(﹣3,﹣2),
∴C(2,﹣1),D(3,2);
(2)设直线AB的解析式为:y=kx+b,
把A,B点代入得:
解得:
故y=3x+7,
当y=0时,x=,
由(1)得:A到x轴距离为:1,B到x轴距离为:2,
∴SABCD=4×=14.
20.解:(1)图中△ADC和三角形EDB成中心对称;
(2)∵△ADC和三角形EDB成中心对称,△ADC的面积为4,
∴△EDB的面积也为4,
∵D为BC的中点,
∴△ABD的面积也为4,
所以△ABE的面积为8;
(3)∵在△ABD和△ECD中,,
∴△ABD≌△ECD(SAS),
∴AB=EC,
∵△ACE中,AB﹣AC<AE<AC+AB,
∴2<AE<8,
∴1<AD<4.
21.解:(1)甲图:平行四边形,
(2)乙图:等腰梯形,
(3)丙图:正方形.
22.解:(1)根据对称中心的性质,可得
对称中心的坐标是D1D的中点,
∵D1,D的坐标分别是(0,3),(0,2),
∴对称中心的坐标是(0,2.5).
(2)∵A,D的坐标分别是(0,4),(0,2),
∴正方形ABCD与正方形A1B1C1D1的边长都是:4﹣2=2,
∴B,C的坐标分别是(﹣2,4),(﹣2,2),
∵A1D1=2,D1的坐标是(0,3),
∴A1的坐标是(0,1),
∴B1,C1的坐标分别是(2,1),(2,3),
综上,可得顶点B,C,B1,C1的坐标分别是(﹣2,4),(﹣2,2),(2,1),(2,3).
23.(1)证明:∵△ABM与△ACM关于直线AF成轴对称,
∴△ABM≌△ACM,
∴AB=AC,
又∵△ABE与△DCE关于点E成中心对称,
∴△ABE≌△DCE,
∴AB=CD,
∴AC=CD;
(2)解:∠F=∠MCD.
理由:由(1)可得∠BAE=∠CAE=∠CDE,∠CMA=∠BMA,
∵∠BAC=2∠MPC,∠BMA=∠PMF,
∴设∠MPC=α,则∠BAE=∠CAE=∠CDE=α,
设∠BMA=β,则∠PMF=∠CMA=β,
∴∠F=∠CPM﹣∠PMF=α﹣β,
∠MCD=∠CDE﹣∠DMC=α﹣β,
∴∠F=∠MCD.
24.解:(1)如图,连接AC交BO于点D,
∵四边形OABC是平行四边形,
∴点D是?OABC的对称中心,
∵OB=4,
∴OD=OB=2,
∴?OABC的对称中心的坐标为:(2,0);
(2)如图,作CE⊥OB于E,AF⊥OB于F,则CE∥AF,
又AD=DC,
∴DE=DF,CE=AF=1,即a=1,
∵OB=4,OF=3,
∴BF=1,
∴OE=1,即b=1,
∴a+b=1+1=2.
25.解:∵ABCD关于点O中心对称,
∴AO=COAB=CDBC=AD.
∵OE⊥AC,
∴AE=EC,
∴C△ABE=AB+BE+AE=AB+BE+EC=AB+BC=24
∴C四边形ABCD=AB+BC+CD+AD=2(AB+BC)=48cm.
26.证明:(1)∵四边形ABCD是中心对称图形,
∴AD=BC,∠ADE=∠CBF,
在△ADE和△CBF中,,
∴△ADE≌△CBF(SAS);
(2)∵△ADE≌△CBF,
∴∠AED=∠CFB,
∴180°﹣∠AED=180°﹣∠CFB,
即∠AEF=∠CFE,
∴AE∥CF.
1.下列图形中,可以看作既是轴对称图形又是中心对称图形的是( )
A.B.C.D.
2.下列图形中,既是轴对称图形又是中心对称图形的是( )
A.角 B.等腰三角形 C.平行四边形 D.正六边形
3.下列图形中,可以看作是中心对称图形的是( )
A. B. C. D.
4.已知点A(2,7),B(﹣5,0),C(0,﹣1),在平面直角坐标系中△A'B'C'以点P(5,6)为对称中心与△ABC成中心对称,则点A'的坐标为( )
A.(﹣2,﹣7) B.(7,2) C.(8,8) D.(8,5)
5.平面直角坐标系中,△OA1B1是边长为2的等边三角形,作△B2A2B1与△OA1B1关于点B1成中心对称,再作△B2A3B3与△B2A2B1关于点B2成中心对称,如此作下去,则△B2020A2021B2021(n是正整数)的顶点A2021的坐标是( )
A.(4041,) B.(4041,﹣) C.(4043,) D.(4043,﹣)
6.把四张扑克牌所摆放的顺序与位置如下,小杨同学选取其中一张扑克牌把他颠倒后再放回原来的位置,那么扑克牌的摆放顺序与位置都没变化,那么小杨同学所选的扑克牌是( )
A. B. C. D.
7.点O是平行四边形ABCD的对称中心,AD>AB,E、F分别是AB边上的点,且EF=AB;G、H分别是BC边上的点,且GH=BC;若S1,S2分别表示△EOF和△GOH的面积,则S1,S2之间的等量关系是S1= S2.
8.如图,三个边长均为2的正方形重叠在一起,O1,O2是其中两个正方形的对角线交点,若把这样的n个小正方形按如图所示方式摆放,则重叠部分的面积为 .
9.如图,将△ABC绕点C(0,﹣1)旋转180°得到△A′B′C,若点A的坐标为(﹣4,﹣3),则点A′的坐标为 .
10.如图,在平面直角坐标系中将△ABC向右平移3个单位长度后得到△A1B1C1,再将△A1B1C1绕点O旋转180°后得到△A2B2C2,则B2C的长度是 .
11.如图,△ABC和△DEC关于点C成中心对称,若AC=1,AB=2,∠BAC=90°,则AE的长是 .
12.如图中阴影部分是由4个完全相同的的正方形拼接而成,若要在①,②,③,④四个区域中的某个区域处添加一个同样的正方形,使它与阴影部分组成的新图形是中心对称图形,则这个正方形应该添加在 处(填写区域对应的序号).
13.在平面直角坐标系中,点P(4,1)关于点(2,0)中心对称的点的坐标是 .
14.如图,在平面直角坐标系中,若△ABC与△DEF关于点H成中心对称,则对称中心H点的坐标是 .
15.如图,把一个如图所示的“俄罗斯方块”图案放到平面直角坐标系中,每个小正方形的边长都是1个单位长度,经过原点的一条直线l将这个图案分成面积相等的两部分,则该直线的函数关系式为 .
16.如图,在平面直角坐标系中,对△ABC进行循环反复的轴对称或中心对称变换,若原来点A的坐标是(a,b),则经过第2020次变换后所得的A点坐标是 .
17.如图,小明家的住房平面图呈长方形,被分割成3个正方形和2个长方形后仍是中心对称图形.若只知道原住房平面图长方形的周长,则分割后不用测量就能知道周长的图形的标号为 .
18.如图所示,△AOD和△COB关于点O中心对称,∠AOD=60°,∠ADO=90°,BD=12,点P是AO上一动点,点Q是OC上一动点,(P、Q不与端点重合),且AP=OQ,连接BQ,DP,则DP+BQ的最小值是 .
19.如图,已知?ABCD的对称中心在原点O,且A(﹣2,1),B(﹣3,﹣2).
(1)求C点及D点的坐标;
(2)求平行四边形ABCD的面积.
20.如图,D是△ABC边BC的中点,连接AD并延长到点E,使DE=AD,连接BE.
(1)哪两个图形成中心对称?
(2)已知△ADC的面积为4,求△ABE的面积;
(3)已知AB=5,AC=3,求AD的取值范围.
21.如图,方格纸中有三个点A,B,C,要求作一个四边形使这三个点在这个四边形的边(包括顶点)上,且四边形的顶点在方格的顶点上.
(1)在甲图中作出的四边形是中心对称图形但不是轴对称图形;
(2)在乙图中作出的四边形是轴对称图形但不是中心对称图形;
(3)在丙图中作出的四边形既是轴对称图形又是中心对称图形.
22.如图,正方形ABCD与正方形A1B1C1D1关于某点中心对称,已知A,D1,D三点的坐标分别是(0,4),(0,3),(0,2).
(1)求对称中心的坐标.
(2)写出顶点B,C,B1,C1的坐标.
23.已知:如图,三角形ABM与三角形ACM关于直线AF成轴对称,三角形ABE与三角形DCE关于点E成中心对称,点E、D、M都在线段AF上,BM的延长线交CF于点P.
(1)求证:AC=CD;
(2)若∠BAC=2∠MPC,请你判断∠F与∠MCD的数量关系,并说明理由.
24.如图所示,已知?OABC,其中点O,A,B,C的坐标分别为O(0,0),A(3,a),B(4,0),C(b,﹣1),求:
(1)?OABC的对称中心的坐标.
(2)a+b的值.
25.四边形ABCD是以点O为对称中心的中心对称图形,过点O作OE⊥AC交BC于点E,如果△ABE的周长为24cm,求四边形ABCD的周长.
26.如图,已知四边形ABCD是中心对称图形,E、F是对角线BD上的两点,且DE=BF,求证:
(1)△ADE≌△CBF;
(2)AE∥CF.
参考答案
1.解:A、不是轴对称图形,是中心对称图形,故本选项不合题意;
B、不是轴对称图形,是中心对称图形,故本选项不合题意;
C、是轴对称图形,不是中心对称图形,故本选项不合题意;
D、既是轴对称图形,又是中心对称图形,故本选项符合题意.
故选:D.
2.解:A.角是轴对称图形,不是中心对称图形,故本选项不符合题意;
B.等腰三角形是轴对称图形,不是中心对称图形,故本选项不符合题意;
C.平行四边形不是轴对称图形,是中心对称图形,故本选项不符合题意;
D.正六边形既是轴对称图形又是中心对称图形,故本选项符合题意.
故选:D.
3.解:A.旋转180°,与原图形能够完全重合是中心对称图形;故此选项符合题意;
B.旋转180°,不能与原图形能够完全重合不是中心对称图形;故此选项不合题意;
C.旋转180°,不能与原图形能够完全重合不是中心对称图形;故此选项不合题意;
D.旋转180°,不能与原图形能够完全重合不是中心对称图形;故此选项不合题意;
故选:A.
4.解:设A′(m,n),
由题意,A(2,7),A′(m,n)关于P(5,6)对称,
∴5=,6=,
∴m=8,n=5,
∴A′(8,5),
故选:D.
5.解:∵△OA1B1是边长为2的等边三角形,
∴A1的坐标为:(1,),B1的坐标为:(2,0),
∵△B2A2B1与△OA1B1关于点B1成中心对称,
∴点A2与点A1关于点B1成中心对称,
∵2×2﹣1=3,2×0﹣=﹣,
∴点A2的坐标是:(3,﹣),
∵△B2A3B3与△B2A2B1关于点B2成中心对称,
∴点A3与点A2关于点B2成中心对称,
∵2×4﹣3=5,2×0﹣(﹣)=,
∴点A3的坐标是:(5,),
∵△B3A4B4与△B3A3B2关于点B3成中心对称,
∴点A4与点A3关于点B3成中心对称,
∵2×6﹣5=7,2×0﹣=﹣,
∴点A4的坐标是:(7,﹣),…,
∵1=2×1﹣1,3=2×2﹣1,5=2×3﹣1,7=2×4﹣1,…,
∴An的横坐标是:2n﹣1,A2n+1的横坐标是:2(2n+1)﹣1=4n+1,
∵当n为奇数时,An的纵坐标是:,当n为偶数时,An的纵坐标是:﹣,
∴顶点A2n+1的纵坐标是:,
∴△B2nA2n+1B2n+1(n是正整数)的顶点A2n+1的坐标是:(4n+1,),
∴△B2020A2021B2021的顶点A2021的横坐标是:4×1010+1=4041,纵坐标是:,
故选:A.
6.解:四张扑克牌:“黑桃7,黑桃8,黑桃9,黑桃10”中,只有黑桃10是中心对称图形,其余的都不是.
故选:D.
7.解:如图,连接OA,OB,OC.设平行四边形的面积为4s.
∵点O是平行四边形ABCD的对称中心,
∴S△AOB=S△BOC=S平行四边形ABCD=s,
∵EF=AB,GH=BC,
∴S1=s,S2=s,
∴==,
故答案为:.
8.解:连接O1B、O1C,如图:
∵∠BO1F+∠FO1C=90°,∠FO1C+∠CO1G=90°,
∴∠BO1F=∠CO1G,
∵四边形ABCD是正方形,
∴∠O1BF=∠O1CG=45°,
在△O1BF和△O1CG中,
,
∴△O1BF≌△O1CG(ASA),
∴O1、O2两个正方形阴影部分的面积是S正方形=1,
同理另外两个正方形阴影部分的面积也是S正方形=1,
∴把这样的n个小正方形按如图所示方式摆放,则重叠部分的面积为(n﹣1).
故答案为:n﹣1
9.解:作A′E⊥y轴于点E,AD⊥y轴于点D,则∠A′EC=∠ADC,
∵∠A′CE=∠ACD,AC=A′C,
∴△A′EC≌△ADC(AAS),
∴AD=A′E=4,CE=CD,
∵OD=3,OC=1,
∴CD=2,
∴CE=2,
∴OE=1,
∴点A′的坐标为(4,1).
故答案为:(4,1).
10.解:如图所示:B2C的长度是:=.
故答案为:.
11.解:∵△DEC与△ABC关于点C成中心对称,
∴△ABC≌△DEC,
∴AB=DE=2,AC=DC=1,∠D=∠BAC=90°,
∴AD=2,
∵∠D=90°,
∴AE==2,
故答案为2.
12.解:把正方形添加在②处,使它与阴影部分组成的新图形是中心对称图形,
故答案为:②.
13.解:如图所示:点P(4,1)关于点(2,0)中心对称的点的坐标是:(0,﹣1).
故答案为:(0,﹣1).
14.解:如图,连接AD、CF,则交点就是对称中心H点.
观察图形可知,H(2,﹣1).
故答案为:(2,﹣1).
15.解:设直线l与俄罗斯方块交于点A.
∵直线l将这个图案分成面积相等的两部分,
∴S△OAB==,
即=,
×2×AB=,
AB=,
∴A(2,),
设直线l解析式y=kx,
将A(2,)代入,得=2k,
解得k=,
∴该直线的函数关系式为y=x,
故答案为y=x.
16.解:点A第一次关于原点对称后在第四象限,
点A第二次关于x轴后在第三象限,
点A第三次关于y轴对称后在第二象限,即点A回到原始位置,
所以,每3次对称为一个循环组依次循环,
∵用2020÷3=673余1,
∴经过第2020次变换后所得的A点与第四次变换的位置相同,在第四象限,坐标为(﹣a,﹣b).
故答案为:(﹣a,﹣b).
17.解:如图1:
设图形①的长和宽分别是a、c,图形②的边长是b,图形③的边长是d,原来大长方形的周长是l,
则l=2(a+2b+c),
根据图示,可得,
①﹣②,可得:a﹣b=b﹣c,
∴2b=a+c,
∴l=2(a+2b+c)=2×2(a+c)=4(a+c),或l=2(a+2b+c)=2×4b=8b,
∴2(a+c)=,4b=,
∵图形①的周长是2(a+c),图形②的周长是4b,的值一定,
∴图形①②的周长是定值,不用测量就能知道,图形③的周长不用测量无法知道.
∴分割后不用测量就能知道周长的图形的标号为①②.
故答案为:①②.
18.解:DP+BQ最小值是12;理由如下:
当AP=OP时,DP+BQ的值最小,此时P为OA的中点,
∵∠ADO=90°,
∴DP=OA=6,
同理BQ=6,
∴DP+BQ的最小值=6+6=12,
故答案为:12
19.解:(1)∵四边形ABCD是平行四边形,
∴四边形ABCD关于O中心对称,
∵A(﹣2,1),B(﹣3,﹣2),
∴C(2,﹣1),D(3,2);
(2)设直线AB的解析式为:y=kx+b,
把A,B点代入得:
解得:
故y=3x+7,
当y=0时,x=,
由(1)得:A到x轴距离为:1,B到x轴距离为:2,
∴SABCD=4×=14.
20.解:(1)图中△ADC和三角形EDB成中心对称;
(2)∵△ADC和三角形EDB成中心对称,△ADC的面积为4,
∴△EDB的面积也为4,
∵D为BC的中点,
∴△ABD的面积也为4,
所以△ABE的面积为8;
(3)∵在△ABD和△ECD中,,
∴△ABD≌△ECD(SAS),
∴AB=EC,
∵△ACE中,AB﹣AC<AE<AC+AB,
∴2<AE<8,
∴1<AD<4.
21.解:(1)甲图:平行四边形,
(2)乙图:等腰梯形,
(3)丙图:正方形.
22.解:(1)根据对称中心的性质,可得
对称中心的坐标是D1D的中点,
∵D1,D的坐标分别是(0,3),(0,2),
∴对称中心的坐标是(0,2.5).
(2)∵A,D的坐标分别是(0,4),(0,2),
∴正方形ABCD与正方形A1B1C1D1的边长都是:4﹣2=2,
∴B,C的坐标分别是(﹣2,4),(﹣2,2),
∵A1D1=2,D1的坐标是(0,3),
∴A1的坐标是(0,1),
∴B1,C1的坐标分别是(2,1),(2,3),
综上,可得顶点B,C,B1,C1的坐标分别是(﹣2,4),(﹣2,2),(2,1),(2,3).
23.(1)证明:∵△ABM与△ACM关于直线AF成轴对称,
∴△ABM≌△ACM,
∴AB=AC,
又∵△ABE与△DCE关于点E成中心对称,
∴△ABE≌△DCE,
∴AB=CD,
∴AC=CD;
(2)解:∠F=∠MCD.
理由:由(1)可得∠BAE=∠CAE=∠CDE,∠CMA=∠BMA,
∵∠BAC=2∠MPC,∠BMA=∠PMF,
∴设∠MPC=α,则∠BAE=∠CAE=∠CDE=α,
设∠BMA=β,则∠PMF=∠CMA=β,
∴∠F=∠CPM﹣∠PMF=α﹣β,
∠MCD=∠CDE﹣∠DMC=α﹣β,
∴∠F=∠MCD.
24.解:(1)如图,连接AC交BO于点D,
∵四边形OABC是平行四边形,
∴点D是?OABC的对称中心,
∵OB=4,
∴OD=OB=2,
∴?OABC的对称中心的坐标为:(2,0);
(2)如图,作CE⊥OB于E,AF⊥OB于F,则CE∥AF,
又AD=DC,
∴DE=DF,CE=AF=1,即a=1,
∵OB=4,OF=3,
∴BF=1,
∴OE=1,即b=1,
∴a+b=1+1=2.
25.解:∵ABCD关于点O中心对称,
∴AO=COAB=CDBC=AD.
∵OE⊥AC,
∴AE=EC,
∴C△ABE=AB+BE+AE=AB+BE+EC=AB+BC=24
∴C四边形ABCD=AB+BC+CD+AD=2(AB+BC)=48cm.
26.证明:(1)∵四边形ABCD是中心对称图形,
∴AD=BC,∠ADE=∠CBF,
在△ADE和△CBF中,,
∴△ADE≌△CBF(SAS);
(2)∵△ADE≌△CBF,
∴∠AED=∠CFB,
∴180°﹣∠AED=180°﹣∠CFB,
即∠AEF=∠CFE,
∴AE∥CF.
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
