第六章 特殊平行四边形及梯形(单元测试)
文档属性
| 名称 | 第六章 特殊平行四边形及梯形(单元测试) |

|
|
| 格式 | zip | ||
| 文件大小 | 186.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-03-17 00:00:00 | ||
图片预览

文档简介
第六章 特殊平行四边形及梯形
一、选择题(每小题3分,共30分)
1.下列说法正确的是 ( )
A.两条对角线相等的四边形是矩形
B.两条对角线互相垂直的四边形是菱形
C.有一条对角线平分一个内角的平行四边形是菱形
D.四条边相等的四边形是正方形
2.如图,在等腰梯形ABCD中,AB∥CD,DC=3 cm,∠A=60°,BD平分∠ABC,则这个梯形的周长是 ( )
A.21 cm B.18 cm
C.15 cm D.12 cm
3.有下列图形:①平行四边形:②菱形;③矩形;④正方形;⑤等腰梯形;⑥线段;⑦角,其中既是中心对称图形又是轴对称图形的有 ( )
A.2个 B.3个 C.4个 D.5个
4.顺次连结矩形的各边中点,所得四边形是 ( )
A.平行四边形 B.矩形 C.菱形 D.正方形
5.菱形和矩形都具有的性质是 ( )
A.对角线相等 B.对角线互相平分
C.对角线平分一组对角 D.对角线互相垂直
6.一个等腰梯形的两底之差为12,高为6,则等腰梯形的锐角为 ( )
A.30° B.45° C.60° D.75°
7.小红画了两条相等并且垂直的线段,以它们为对角线的四边形是 ( )
A.平行四边形 B.菱形 C.正方形 D.无法确定
8.己知正方形ABCD中,对角线长为2 cm,点E是AB边上任意一点,则E到两条对角线距离之和是 ( )
A.2cm B.1 cm C.2 cm D.cm
9.在以下五个图形中:①平行四边形;②菱形;③矩形;④正方形;⑤三角形.一定能够找到一点,使该点到各边距离都相等的是 ( )
A.①② B.②③④⑤ C.②④ D.②④⑤
10.如图,在矩形ABCD中,BC=2,AE⊥BD于点E,若∠BAE=30°,则S△ECD=( )
A. B. C. D.3
二、填空题(每小题3分,共30分)
11.如果□ABCD满足条件: (只需添一种情况),那么这个平行四边形是矩形.
12.如图,在矩形ABCD中,对角线AC,BD交于点O,若∠AOD=120°,AB=1,则AC= ,BC=— .21世纪教育网
13.在菱形ABCD中,AB=AC=10,则∠A= ,BD= .
14.已知菱形的周长为40 cm,一条对角线长为l6 cm,则这个菱形的面积是 .
15.在正方形ABCD中,点E是AD的中点,点F是BA延长线上一点,且AF=AB,△ABE可以通过绕A点逆时针旋转到△ADF的位置,则旋转的最小角度为 .
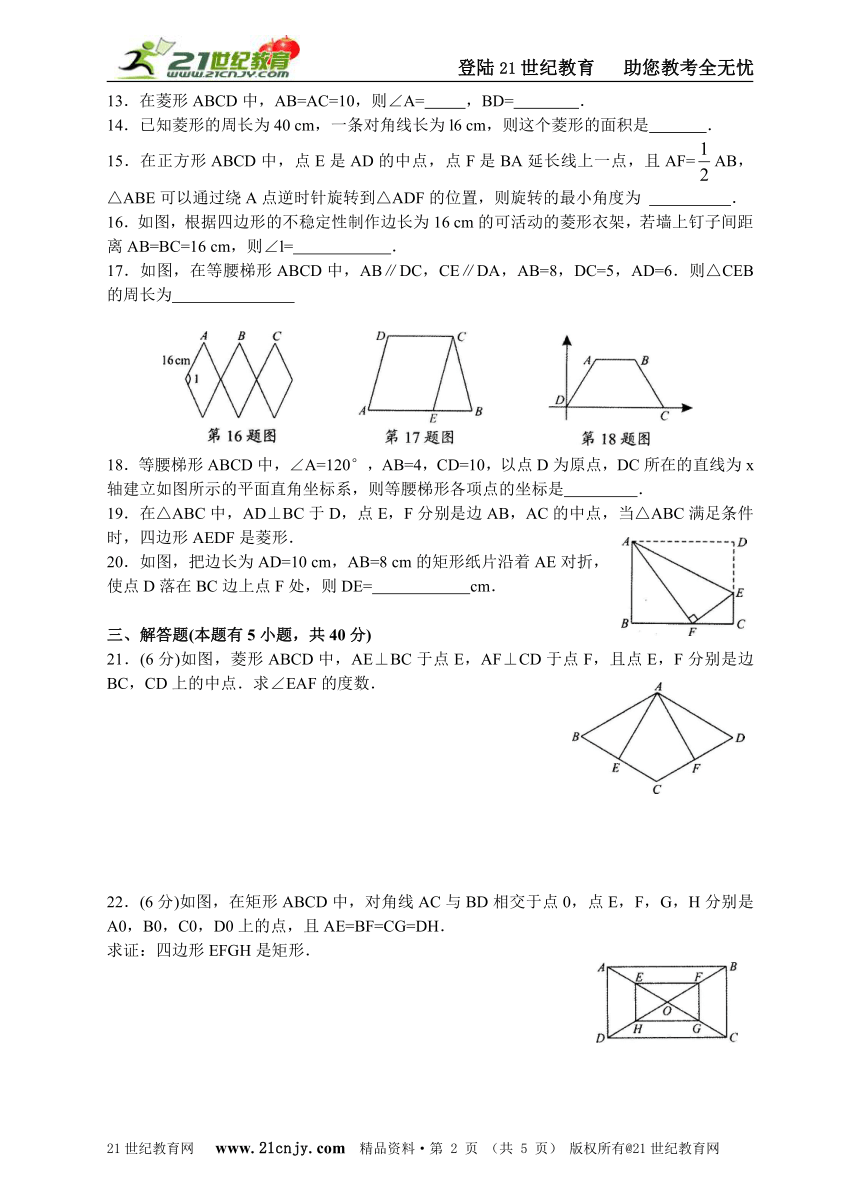
16.如图,根据四边形的不稳定性制作边长为16 cm的可活动的菱形衣架,若墙上钉子间距离AB=BC=16 cm,则∠l= .21世纪教育网
17.如图,在等腰梯形ABCD中,AB∥DC,CE∥DA,AB=8,DC=5,AD=6.则△CEB的周长为 21世纪教育网
18.等腰梯形ABCD中,∠A=120°,AB=4,CD=10,以点D为原点,DC所在的直线为x轴建立如图所示的平面直角坐标系,则等腰梯形各项点的坐标是 .
19.在△ABC中,AD⊥BC于D,点E,F分别是边AB,AC的中点,当△ABC满足条件 时,四边形AEDF是菱形.
20.如图,把边长为AD=10 cm,AB=8 cm的矩形纸片沿着AE对折,使点D落在BC边上点F处,则DE= cm.
三、解答题(本题有5小题,共40分) 21世纪教育网
21.(6分)如图,菱形ABCD中,AE⊥BC于点E,AF⊥CD于点F,且点E,F分别是边BC,CD上的中点.求∠EAF的度数.
22.(6分)如图,在矩形ABCD中,对角线AC与BD相交于点0,点E,F,G,H分别是A0,B0,C0,D0上的点,且AE=BF=CG=DH.
求证:四边形EFGH是矩形.
23.(8分)如图,梯形ABCD中,DC∥AB,对角线AC,BD相交于点E,∠AEB=60°,AC=BD=16, AB=3DC,求梯形ABCD的周长和面积.21世纪教育网
24.(10分)如图,正方形ABCD的边长为l,G为CD边上的一个动点(点G与C,D不重合), 以CG为一边向正方形ABCD外作正方形GCEF,连结DE交BG的延长线于点日.
(1)求证:△BCG≌△DCE;BH⊥DE.21世纪教育网
(2)当点G运动到什么位置时,BH垂直平分DE?请说明理由.
25.(10分)如图,等腰梯形ABCD中,AD∥BC,点M,N分别是边AD,BC的中点,点E,F分别是边BM,CM的中点.
(1)求证:四边形MENF是菱形;
(2)若蓁形MENF是币方形,则梯形的高与底边BC有何关系?试证明你的结论.
第六章特殊平行四边形及梯形
一、l.C 2.C 3.C 4.C 5.B 6.B 7.D 8.D 9.D l0.B
二、ll.有一个角是直角(或对角线相等) 12.2 l3.120° 10 l4.96 cm2 15.90°16.120° 17.15 18.A(3,3),B(7,3),C(10,0),D(0,0) 19.AB=AC(或∠B=∠C) 20.5
三、21.连结AC,则
∵AE⊥BC,且点E为边BC上的中点,
∴AB=AC.
又∵四边形ABCD为菱形,
∴AB=AC,
∴△ABC为等边三角形,
∴∠B=∠BAC=60°,
∴∠EAC=∠BAC=30°.
同理∠CAF=30°.
∴∠EAF=∠EAC+∠CAF=60°.21世纪教育网
22.略(提示:由对角线互相平分且相等得证)
23.周长为8+16,面积为64.
24.(1)证明:∵四边形ABCD,GCEF为正方形,
∴BC=DC,GC=EC,∠BCG=∠DCE=90°,
∴△BCG≌△DCE(SAS);
由上述可知,∠GBC=∠EDC,
又∵在△BCG与△DHG中,∠BGC=∠DGH,
∴∠DHG=∠BCG=90°,
即BH⊥DE.
(2)设CG=x,则BG==,DH=BG=,
由(1)知,△BCG∽△DHG,则
==
即=,x1=—1,x2=——1(不合,舍去)
∴GC=—1时,BH垂直平分DE.
25.(1)由四边形ABCD是等腰梯形,点M为AD上的中点,可证△ABM≌△DCM ∴MB=MC 又∵E,N,F,分别是边BM ,BC,CM上的中点, ∴EN∥MC,EN=MC ,FN∥MB,FN=MB ∴四边形MENF是菱形;
(2)由题意可知,线段MN为该梯形的高.若菱形MENF是正方形,则∠BMC=90°, ∴△MBC为等腰直角三角形, ∴MN=BC.
一、选择题(每小题3分,共30分)
1.下列说法正确的是 ( )
A.两条对角线相等的四边形是矩形
B.两条对角线互相垂直的四边形是菱形
C.有一条对角线平分一个内角的平行四边形是菱形
D.四条边相等的四边形是正方形
2.如图,在等腰梯形ABCD中,AB∥CD,DC=3 cm,∠A=60°,BD平分∠ABC,则这个梯形的周长是 ( )
A.21 cm B.18 cm
C.15 cm D.12 cm
3.有下列图形:①平行四边形:②菱形;③矩形;④正方形;⑤等腰梯形;⑥线段;⑦角,其中既是中心对称图形又是轴对称图形的有 ( )
A.2个 B.3个 C.4个 D.5个
4.顺次连结矩形的各边中点,所得四边形是 ( )
A.平行四边形 B.矩形 C.菱形 D.正方形
5.菱形和矩形都具有的性质是 ( )
A.对角线相等 B.对角线互相平分
C.对角线平分一组对角 D.对角线互相垂直
6.一个等腰梯形的两底之差为12,高为6,则等腰梯形的锐角为 ( )
A.30° B.45° C.60° D.75°
7.小红画了两条相等并且垂直的线段,以它们为对角线的四边形是 ( )
A.平行四边形 B.菱形 C.正方形 D.无法确定
8.己知正方形ABCD中,对角线长为2 cm,点E是AB边上任意一点,则E到两条对角线距离之和是 ( )
A.2cm B.1 cm C.2 cm D.cm
9.在以下五个图形中:①平行四边形;②菱形;③矩形;④正方形;⑤三角形.一定能够找到一点,使该点到各边距离都相等的是 ( )
A.①② B.②③④⑤ C.②④ D.②④⑤
10.如图,在矩形ABCD中,BC=2,AE⊥BD于点E,若∠BAE=30°,则S△ECD=( )
A. B. C. D.3
二、填空题(每小题3分,共30分)
11.如果□ABCD满足条件: (只需添一种情况),那么这个平行四边形是矩形.
12.如图,在矩形ABCD中,对角线AC,BD交于点O,若∠AOD=120°,AB=1,则AC= ,BC=— .21世纪教育网
13.在菱形ABCD中,AB=AC=10,则∠A= ,BD= .
14.已知菱形的周长为40 cm,一条对角线长为l6 cm,则这个菱形的面积是 .
15.在正方形ABCD中,点E是AD的中点,点F是BA延长线上一点,且AF=AB,△ABE可以通过绕A点逆时针旋转到△ADF的位置,则旋转的最小角度为 .
16.如图,根据四边形的不稳定性制作边长为16 cm的可活动的菱形衣架,若墙上钉子间距离AB=BC=16 cm,则∠l= .21世纪教育网
17.如图,在等腰梯形ABCD中,AB∥DC,CE∥DA,AB=8,DC=5,AD=6.则△CEB的周长为 21世纪教育网
18.等腰梯形ABCD中,∠A=120°,AB=4,CD=10,以点D为原点,DC所在的直线为x轴建立如图所示的平面直角坐标系,则等腰梯形各项点的坐标是 .
19.在△ABC中,AD⊥BC于D,点E,F分别是边AB,AC的中点,当△ABC满足条件 时,四边形AEDF是菱形.
20.如图,把边长为AD=10 cm,AB=8 cm的矩形纸片沿着AE对折,使点D落在BC边上点F处,则DE= cm.
三、解答题(本题有5小题,共40分) 21世纪教育网
21.(6分)如图,菱形ABCD中,AE⊥BC于点E,AF⊥CD于点F,且点E,F分别是边BC,CD上的中点.求∠EAF的度数.
22.(6分)如图,在矩形ABCD中,对角线AC与BD相交于点0,点E,F,G,H分别是A0,B0,C0,D0上的点,且AE=BF=CG=DH.
求证:四边形EFGH是矩形.
23.(8分)如图,梯形ABCD中,DC∥AB,对角线AC,BD相交于点E,∠AEB=60°,AC=BD=16, AB=3DC,求梯形ABCD的周长和面积.21世纪教育网
24.(10分)如图,正方形ABCD的边长为l,G为CD边上的一个动点(点G与C,D不重合), 以CG为一边向正方形ABCD外作正方形GCEF,连结DE交BG的延长线于点日.
(1)求证:△BCG≌△DCE;BH⊥DE.21世纪教育网
(2)当点G运动到什么位置时,BH垂直平分DE?请说明理由.
25.(10分)如图,等腰梯形ABCD中,AD∥BC,点M,N分别是边AD,BC的中点,点E,F分别是边BM,CM的中点.
(1)求证:四边形MENF是菱形;
(2)若蓁形MENF是币方形,则梯形的高与底边BC有何关系?试证明你的结论.
第六章特殊平行四边形及梯形
一、l.C 2.C 3.C 4.C 5.B 6.B 7.D 8.D 9.D l0.B
二、ll.有一个角是直角(或对角线相等) 12.2 l3.120° 10 l4.96 cm2 15.90°16.120° 17.15 18.A(3,3),B(7,3),C(10,0),D(0,0) 19.AB=AC(或∠B=∠C) 20.5
三、21.连结AC,则
∵AE⊥BC,且点E为边BC上的中点,
∴AB=AC.
又∵四边形ABCD为菱形,
∴AB=AC,
∴△ABC为等边三角形,
∴∠B=∠BAC=60°,
∴∠EAC=∠BAC=30°.
同理∠CAF=30°.
∴∠EAF=∠EAC+∠CAF=60°.21世纪教育网
22.略(提示:由对角线互相平分且相等得证)
23.周长为8+16,面积为64.
24.(1)证明:∵四边形ABCD,GCEF为正方形,
∴BC=DC,GC=EC,∠BCG=∠DCE=90°,
∴△BCG≌△DCE(SAS);
由上述可知,∠GBC=∠EDC,
又∵在△BCG与△DHG中,∠BGC=∠DGH,
∴∠DHG=∠BCG=90°,
即BH⊥DE.
(2)设CG=x,则BG==,DH=BG=,
由(1)知,△BCG∽△DHG,则
==
即=,x1=—1,x2=——1(不合,舍去)
∴GC=—1时,BH垂直平分DE.
25.(1)由四边形ABCD是等腰梯形,点M为AD上的中点,可证△ABM≌△DCM ∴MB=MC 又∵E,N,F,分别是边BM ,BC,CM上的中点, ∴EN∥MC,EN=MC ,FN∥MB,FN=MB ∴四边形MENF是菱形;
(2)由题意可知,线段MN为该梯形的高.若菱形MENF是正方形,则∠BMC=90°, ∴△MBC为等腰直角三角形, ∴MN=BC.
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
