浙教版八年级下册数学 6.1 反比例函数同步培优练习 (含解析)
文档属性
| 名称 | 浙教版八年级下册数学 6.1 反比例函数同步培优练习 (含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-14 08:43:11 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
6.1反比例函数
一、单选题
1.如图,在平面直角坐标系中,过点0的直线AB交反比例函数y=的图象于点A,B,点c在反比例函数y= (x>0)的图象上,连结CA,CB,当CA=CB且cos∠CAB= 时,k1,k2应满足的数量关系是(?? )
A.k2=2kl B.k2=-2k1 C.k2=4k1 D.k2=-4k1
2.已知:如图,在平面直角坐标系中,有菱形OABC,点A的坐标为(10,0),对角线OB、AC相交于点D,双曲线(x>0)经过点D,交BC的延长线于点E,且OB·AC=160,有下列四个结论:①双曲线的解析式为y=(x>0);②点E的坐标是(4,8);③sin∠COA=;④AC+OB=12.其中正确的结论有( )
A.3个 B.2个 C.1个 D.0个
3.如图,在x轴上方,∠BOA=90°且其两边分别与反比例函数y=﹣、y=的图象交于B、A两点,则∠OAB的正切值为( )
A. B. C. D.
4.如图,反比例函数的图像经过点,过点作轴,垂足为,在轴的正半轴上取一点,过点作直线的垂线,以直线为对称轴,点经轴对称变换得到的点在此反比例函数的图像上,则的值为( ).
A. B. C. D.
5.如图,Rt△OAB的顶点O与坐标原点重合,∠AOB=90°,AO=2BO,当A点在反比例函数 (x>0)的图象上移动时,B点坐标满足的函数解析式为( )
A. B.
C. D.
6.如图,矩形的顶点在反比例函数的图象上,点和点在边上,,连接轴,则的值为( )
A. B.3 C.4 D.
7.将函数 的图象沿轴向右平移个单位长度,得到的图象所相应的函数表达式是( )
A. B. C. D.
8.如图,反比例函数的图象过矩形的顶点,,分别在轴、轴的正半轴上,矩形的对角线,交于点,则的值为( )
A. B. C. D.
9.反比例函数y=的图像如图所示,下列说法正确的是( )
A.k>0
B.y 随x的增大而增大
C.若矩形 OABC的面积为2,则
D.若图像上点B的坐标是(-2,1),则当x<-2时,y的取值范围是y<1
10.经过点的反比例函数的解析式是( )
A. B. C. D.
二、填空题
11.如图,A(1,1),B(2,2),双曲线y=与线段AB有公共点,则k的取值范围是________.
12.如图,菱形的顶点在轴正半轴上,边所在直线过点,对角线轴交于点,双曲线上过点且与交于点,如果,,那么的值为_________.
13.如图,在平面直角坐标系中,菱形OBCD的边OB在x轴正半轴上,反比例函数的图象经过该菱形对角线的交点A,且与边BC交于点F,若点D的坐标为,则反比例函数的解析式为__________.
14.如图,反比例函数的图象经过等边的顶点,,且原点刚好在线段上,已知点的坐标是,则的值为________.
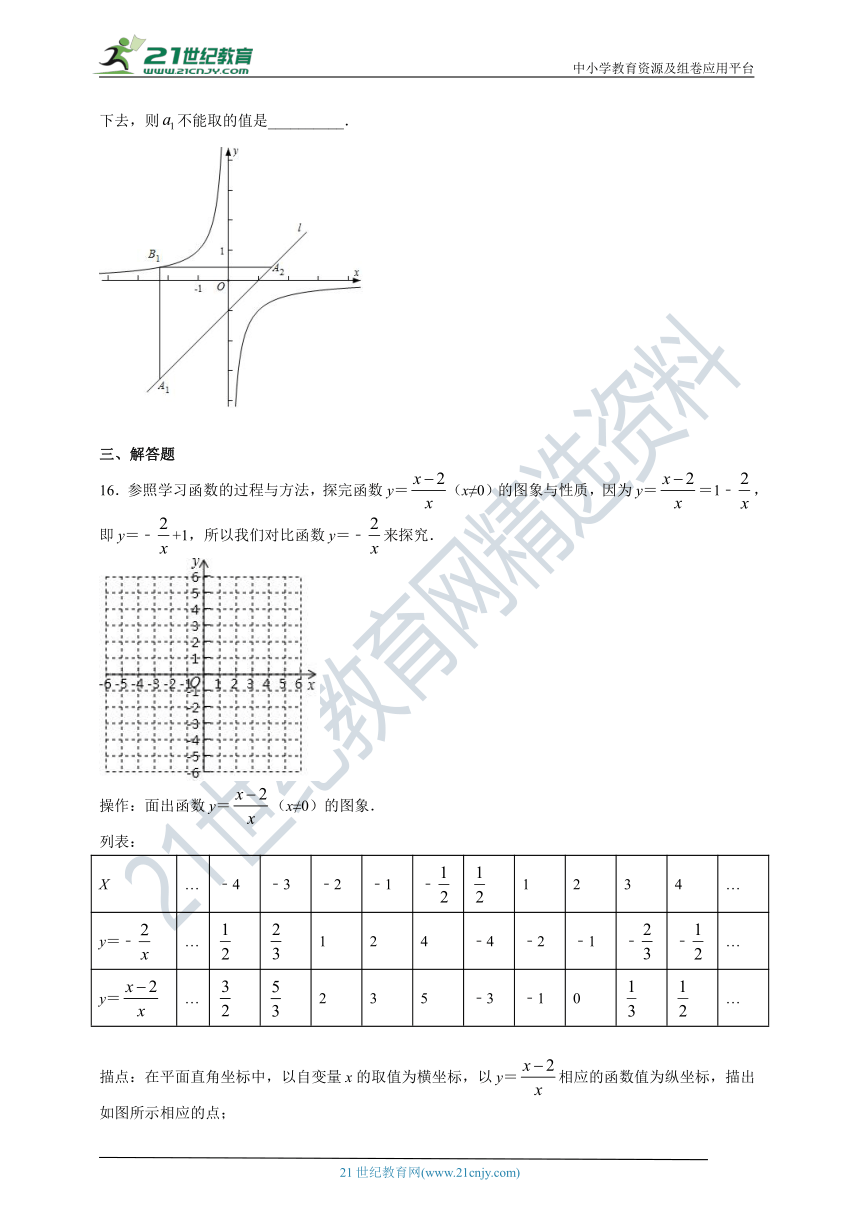
15.如图,在平面直角坐标系中,已知直线,双曲线,在l上取一点,过作轴的垂线交双曲线于点,过作轴的垂线交l于点,请继续操作并探究:过作轴的垂线交双曲线于点,过作轴的垂线交l于点,…,这样依次得到l上的点,,,…,,…,记点的横坐标为,若,则__________;若要将上述操作无限次地进行下去,则不能取的值是__________.
三、解答题
16.参照学习函数的过程与方法,探完函数y=(x≠0)的图象与性质,因为y==1﹣,即y=﹣+1,所以我们对比函数y=﹣来探究.
操作:面出函数y=(x≠0)的图象.
列表:
X … ﹣4 ﹣3 ﹣2 ﹣1 ﹣
1 2 3 4 …
y=﹣ …
1 2 4 ﹣4 ﹣2 ﹣1 ﹣ ﹣ …
y= …
2 3 5 ﹣3 ﹣1 0
…
描点:在平面直角坐标中,以自变量x的取值为横坐标,以y=相应的函数值为纵坐标,描出如图所示相应的点;
连线:请把y轴左边和右边各点,分别用一条光滑曲线顺次连接起来.
观察:由图象可知:
①当x>0时,y随x的增大而 (填“增大”或“减小”)
②y=的图象可以由y=﹣的图象向 平移 个单位长度得到.
③y的取值范围是 .
探究:①A(m1,n1),B(m2,n2)在函数y=图象上,且n1+n2=2,求m1+m2的值;
②若直线l对应的函数关系式为y1=kx+b,且经过点(﹣1,3)和点(1,﹣1),y2=,若y1>y2,则x的取值范围为 .
延伸:函数y=的图象可以由反比例函数y= 的图象向 平移 个单位,再向 平移 个单位得到.
17.如图,网格线的交点称为格点,双曲线与直线在第一象限交于格点.
(1)填空:
(2)双曲线与直线的另一个交点的坐标为在图中标出来.
(3)在如图所示的网格中仅用直尺,铅笔画,且满足以下条件:
①使的面积为,其中点为格点;
②这样的画出四个即可.
18.如图,在直角坐标系中,直线与反比例函数的图象交于关于原点对称的,两点,已知点的纵坐标是3.
(1)求反比例函数的表达式;
(2)将直线向上平移后与反比例函数在第二象限内交于点,如果的面积为36,求平移后的直线的函数表达式.
参考答案
1.D
【解析】
分析:连接OC,过点AE⊥x轴于点E,过点C作CF⊥x轴于点F,利用反比例函数的性质及等腰三角形的性质,可证得CO⊥AB,利用锐角三角函数的定义,可得出, 设OA=x, AC=5x,求出OC的长,再证明△AOE∽△OCF,根据相似三角形的性质,得出OF=2AE,CF=2OE,可得出OFCF=4AEOE,然后根据反比例函数的几何意义,可得出k2与k1的关系,即可得出答案.
详解:连接OC,过点AE⊥x轴于点E,过点C作CF⊥x轴于点F
∴∠AEO=∠CFO=90°
∴∠OAE+∠AOE=90°
∵OA=OB,CA=CB
∴CO⊥AB
∴∠AOC=90°
在Rt△AOC中,cos∠CAB=
设OA=x, AC=5x
∴OC==2x
∵∠AOE+∠COF=90°
∴∠AOE=∠COF
∴△AOE∽△OCF
∴
∴OF=2AE,CF=2OE
∴OFCF=4AEOE
根据题意得:AEOE=|k1|,OFCF=|k2|,k2>0,k1<0
∴k2=-4k1
故选:D.
点睛:此题主要考查了反比例函数系数k的几何意义与相似三角形的判定与性质,关键是通过反比例函数的图像确定△AOE∽△OCF,综合性比较强,有一定的难度,解题时要细心对待.
2.A
【详解】
① 过点C
作CM⊥x轴于点M,如图1所示.
∵OB?AC=160,四边形OABC为菱形,
∴S△OCA=OA?CM=OB?AC=40,
∵A点的坐标为(10,0),
∴OA=10
∴CM=8,
∴OM==6,
∴点C(6,8),
∴点B(16,8).
∵点D为线段OB的中点,
∴点D(8,4),
∵双曲线经过D点,
∴k=8×4=32,
∴双曲线的解析式为y=
∴①不正确;
②∵点E在双曲线y=的图象上,且E点的纵坐标为8,
∴32÷8=4,
∴点E(4,8),
∴②正确;
③∵sin∠COA==,
∴③正确;
④在Rt△CMA中,CM=8,AM=OA-OM=10-6=4,
∴AC===4,
∵OB?AC=160,
∴OB=8
∴AC+OB=12
∴④成立.
综上可知:②③④成立.
故答案为:A
3.B
【详解】如图,分别过点A、B作AN⊥x轴、BM⊥x轴;
∵∠AOB=90°,
∴∠BOM+∠AON=∠AON+∠OAN=90°,
∴∠BOM=∠OAN,
∵∠BMO=∠ANO=90°,
∴△BOM∽△OAN,
∴,
设设B(-m,),A(n,),
则BM=,AN=,OM=m,ON=n,
∴mn=,mn=;
∵∠AOB=90°,
∴tan∠OAB=①;
∵△BOM∽△OAN,
∴= ==②,
由①②知tan∠OAB=.
故正确选项为:B.
4.C
【解析】
如图:
∵点坐标为,
∴,
∴反比例函数解析式为,
∵,
∴为等腰直角三角形,
∴,
∵,
∴,
∵点和点关于直线对称,
∴,,
∴,,
∴轴,
∴点的坐标为,
∵,
∵,
整理得,
解得,(不符合体意,舍去),
∴的值为.
故选:.
5.B
【解析】
【详解】
解:如图过点A作AC⊥x轴于点C,过点B作BD⊥x轴于点D,
设B点坐标满足的函数解析式是
∵∠ACO=∠BDO=90°
∴∠AOC+∠0AC=90°,
∵∠AOB=90°,
∴∠AOC+∠BOD=90°,
∴.∠BOD=∠0AC,
∴△AOC∽△OBD,
∴
∵当A点在反比例函数y=-(x>0)的图象上移动,
解得:k=
∴B点坐标满足的函数解析式
故答案为:B.
6.C
【详解】
解:∵,,x轴⊥y轴,
∴OE=OF=1,∠FOE=90°,∠OEF=∠OFE=45°,
∴,
∴,
∵四边形ABCD为矩形,
∴∠A=90°,
∵轴,
∴∠DFE=∠OEF=45°,
∴∠ADF=45°,,
∴
∴D(4,1),
∴,解得,
故选:C.
7.B
【详解】
解:将函数的图象沿x轴向右平移1个单位长度,得到的图象所相应的函数表达式是,
故选:B.
8.B
【详解】
解:由题意可得A的横坐标为1×2=2,C的纵坐标为2×2=4,
∴B的坐标为(2,4),
∵B在反比例函数图象上,
∴
∴k=2×4=8,
故选B.
9.C
【详解】
解:A、反比例函数图象分布在第二、四象限,则k<0,所以A选项错误;
B、在每一象限,y随x的增大而增大,所以B选项错误;
C、矩形OABC面积为2,则|k|=2,而k<0,所以k=﹣2,所以C选项正确;
D、若图象上点B的坐标是(﹣2,1),则当x<﹣2时,y的取值范围是0<y<1,所以D选项错误.
故选C
10.C
【详解】
设反比例函数解析式为,
把点代入得:,
∴;
故答案选C.
11.1≤k≤4.
【详解】
解:当点A在双曲线上时,k=1
当点B在双曲线上时,k=4,∴双曲线与线段AB有公共点,则k的取值范围为1≤k≤4.
故答案为:1≤k≤4
12.9
【详解】
解:设,,则,
设,,
则,解得:,
在双曲线上,
,
故答案为:9.
13.
【详解】
过点D作DM⊥x轴于点M,
∵点D的坐标为(6,8),
∴OD=,
∵四边形OBCD是菱形,
∴OB=OD=10,
∴点B的坐标为:(10,0),
∵AB=AD,即A是BD的中点,
∴点A的坐标为:(,),即(8,4),
∵点A在反比例函数的图象上,
∴,
∴反比例函数的解析式为.
故答案为:.
14.3
【详解】
解:连结OC,过C作CD⊥x轴于D,BE⊥x轴于E,
由对称性可知:OA=OB,
∵△ABC是等边三角形,
∴OC⊥AB,
∵C(-3,3),
∴OC=3,
∴OB=OC=,
∵OD=CD=3,
∴∠DOC=∠DCO=45?,
∴∠EOB=90?-∠DOC=90?-45?=45?,
∴OE=BE,
在Rt△BEO中OE2+BE2=OB2=6,
∴OE=BE=,
∵点B在第三象限,
∴B(-,﹣),
把B点坐标代入y=,得到k=3,
故答案为:3.
15. 0、1
【详解】
解:当时,的纵坐标为,
的纵坐标和的纵坐标相同,则的横坐标为,
的横坐标和的横坐标相同,则的纵坐标为,
的纵坐标和的纵坐标相同,则的横坐标为,
的横坐标和的横坐标相同,则的纵坐标为,
的纵坐标和的纵坐标相同,则的横坐标为,
的横坐标和的横坐标相同,则的纵坐标为,
即当时,,,,,
,,,,,
,
;
点不能在轴上(此时找不到),即,
点不能在轴上(此时,在轴上,找不到),即,
解得:;
综上可得不可取0、1.
故答案为:;0、1.
16.观察:①增大;②上,1;③y≠1;探究:①m1+m2=0;②x<﹣1或0<x<1;0延伸:,左,1,下,2.
【详解】
操作:函数图象如图所示:
观察:①当x<0时,y随x的增大而增大;
②y=的图象是由y=﹣的图象向上平移1个单位长度得到.
③y的取值范围是y≠1.
故答案为:增大,上,1,y≠1;
探究:①y==1﹣,
∵A(m1,n1),B(m2,n2)在函数y=图象上,
∴n1=1﹣,n2=1﹣,
∵n1+n2=2,
∴=0,
∴=0,
∴m1+m2=0;
②由图象可知,
根据题意得:若y1>y2,则x的取值范围为x<﹣1或0<x<1,
故答案为x<﹣1或0<x<1;
延伸:函数y=的图象可以由反比例函数y=的图象向左平移1个单位,再向下平移2个单位得到,
故答案为,左,1,下,2.
17.(1);(2)见解析;(3)①见解析,②见解析
【详解】
解:(1)由图可知,点A为(3,2),则有
,
∴;
故答案为:;;
;
∵,
∵点A(3,2),B(,2),
∴,,
∴在如图的网格中可以画出的点有个,它们的坐标分别为
只需画出四个即可;
.
18.(1);(2)
【详解】
(1)根据题意得:
解得:,即点的坐标为
∵点在反比例函数的图象上,
∴
∴反比例函数的表达式为;
(2)如图,设平移后的直线与轴交于点,连接,
设平移后的解析式为,
∴
∵该直线平行直线,
∴
∵的面积为36,
∴
由对称性可知:,
∴
∴
∴
∴平移后的直线的函数表达式为.
_21?????????è?????(www.21cnjy.com)_
6.1反比例函数
一、单选题
1.如图,在平面直角坐标系中,过点0的直线AB交反比例函数y=的图象于点A,B,点c在反比例函数y= (x>0)的图象上,连结CA,CB,当CA=CB且cos∠CAB= 时,k1,k2应满足的数量关系是(?? )
A.k2=2kl B.k2=-2k1 C.k2=4k1 D.k2=-4k1
2.已知:如图,在平面直角坐标系中,有菱形OABC,点A的坐标为(10,0),对角线OB、AC相交于点D,双曲线(x>0)经过点D,交BC的延长线于点E,且OB·AC=160,有下列四个结论:①双曲线的解析式为y=(x>0);②点E的坐标是(4,8);③sin∠COA=;④AC+OB=12.其中正确的结论有( )
A.3个 B.2个 C.1个 D.0个
3.如图,在x轴上方,∠BOA=90°且其两边分别与反比例函数y=﹣、y=的图象交于B、A两点,则∠OAB的正切值为( )
A. B. C. D.
4.如图,反比例函数的图像经过点,过点作轴,垂足为,在轴的正半轴上取一点,过点作直线的垂线,以直线为对称轴,点经轴对称变换得到的点在此反比例函数的图像上,则的值为( ).
A. B. C. D.
5.如图,Rt△OAB的顶点O与坐标原点重合,∠AOB=90°,AO=2BO,当A点在反比例函数 (x>0)的图象上移动时,B点坐标满足的函数解析式为( )
A. B.
C. D.
6.如图,矩形的顶点在反比例函数的图象上,点和点在边上,,连接轴,则的值为( )
A. B.3 C.4 D.
7.将函数 的图象沿轴向右平移个单位长度,得到的图象所相应的函数表达式是( )
A. B. C. D.
8.如图,反比例函数的图象过矩形的顶点,,分别在轴、轴的正半轴上,矩形的对角线,交于点,则的值为( )
A. B. C. D.
9.反比例函数y=的图像如图所示,下列说法正确的是( )
A.k>0
B.y 随x的增大而增大
C.若矩形 OABC的面积为2,则
D.若图像上点B的坐标是(-2,1),则当x<-2时,y的取值范围是y<1
10.经过点的反比例函数的解析式是( )
A. B. C. D.
二、填空题
11.如图,A(1,1),B(2,2),双曲线y=与线段AB有公共点,则k的取值范围是________.
12.如图,菱形的顶点在轴正半轴上,边所在直线过点,对角线轴交于点,双曲线上过点且与交于点,如果,,那么的值为_________.
13.如图,在平面直角坐标系中,菱形OBCD的边OB在x轴正半轴上,反比例函数的图象经过该菱形对角线的交点A,且与边BC交于点F,若点D的坐标为,则反比例函数的解析式为__________.
14.如图,反比例函数的图象经过等边的顶点,,且原点刚好在线段上,已知点的坐标是,则的值为________.
15.如图,在平面直角坐标系中,已知直线,双曲线,在l上取一点,过作轴的垂线交双曲线于点,过作轴的垂线交l于点,请继续操作并探究:过作轴的垂线交双曲线于点,过作轴的垂线交l于点,…,这样依次得到l上的点,,,…,,…,记点的横坐标为,若,则__________;若要将上述操作无限次地进行下去,则不能取的值是__________.
三、解答题
16.参照学习函数的过程与方法,探完函数y=(x≠0)的图象与性质,因为y==1﹣,即y=﹣+1,所以我们对比函数y=﹣来探究.
操作:面出函数y=(x≠0)的图象.
列表:
X … ﹣4 ﹣3 ﹣2 ﹣1 ﹣
1 2 3 4 …
y=﹣ …
1 2 4 ﹣4 ﹣2 ﹣1 ﹣ ﹣ …
y= …
2 3 5 ﹣3 ﹣1 0
…
描点:在平面直角坐标中,以自变量x的取值为横坐标,以y=相应的函数值为纵坐标,描出如图所示相应的点;
连线:请把y轴左边和右边各点,分别用一条光滑曲线顺次连接起来.
观察:由图象可知:
①当x>0时,y随x的增大而 (填“增大”或“减小”)
②y=的图象可以由y=﹣的图象向 平移 个单位长度得到.
③y的取值范围是 .
探究:①A(m1,n1),B(m2,n2)在函数y=图象上,且n1+n2=2,求m1+m2的值;
②若直线l对应的函数关系式为y1=kx+b,且经过点(﹣1,3)和点(1,﹣1),y2=,若y1>y2,则x的取值范围为 .
延伸:函数y=的图象可以由反比例函数y= 的图象向 平移 个单位,再向 平移 个单位得到.
17.如图,网格线的交点称为格点,双曲线与直线在第一象限交于格点.
(1)填空:
(2)双曲线与直线的另一个交点的坐标为在图中标出来.
(3)在如图所示的网格中仅用直尺,铅笔画,且满足以下条件:
①使的面积为,其中点为格点;
②这样的画出四个即可.
18.如图,在直角坐标系中,直线与反比例函数的图象交于关于原点对称的,两点,已知点的纵坐标是3.
(1)求反比例函数的表达式;
(2)将直线向上平移后与反比例函数在第二象限内交于点,如果的面积为36,求平移后的直线的函数表达式.
参考答案
1.D
【解析】
分析:连接OC,过点AE⊥x轴于点E,过点C作CF⊥x轴于点F,利用反比例函数的性质及等腰三角形的性质,可证得CO⊥AB,利用锐角三角函数的定义,可得出, 设OA=x, AC=5x,求出OC的长,再证明△AOE∽△OCF,根据相似三角形的性质,得出OF=2AE,CF=2OE,可得出OFCF=4AEOE,然后根据反比例函数的几何意义,可得出k2与k1的关系,即可得出答案.
详解:连接OC,过点AE⊥x轴于点E,过点C作CF⊥x轴于点F
∴∠AEO=∠CFO=90°
∴∠OAE+∠AOE=90°
∵OA=OB,CA=CB
∴CO⊥AB
∴∠AOC=90°
在Rt△AOC中,cos∠CAB=
设OA=x, AC=5x
∴OC==2x
∵∠AOE+∠COF=90°
∴∠AOE=∠COF
∴△AOE∽△OCF
∴
∴OF=2AE,CF=2OE
∴OFCF=4AEOE
根据题意得:AEOE=|k1|,OFCF=|k2|,k2>0,k1<0
∴k2=-4k1
故选:D.
点睛:此题主要考查了反比例函数系数k的几何意义与相似三角形的判定与性质,关键是通过反比例函数的图像确定△AOE∽△OCF,综合性比较强,有一定的难度,解题时要细心对待.
2.A
【详解】
① 过点C
作CM⊥x轴于点M,如图1所示.
∵OB?AC=160,四边形OABC为菱形,
∴S△OCA=OA?CM=OB?AC=40,
∵A点的坐标为(10,0),
∴OA=10
∴CM=8,
∴OM==6,
∴点C(6,8),
∴点B(16,8).
∵点D为线段OB的中点,
∴点D(8,4),
∵双曲线经过D点,
∴k=8×4=32,
∴双曲线的解析式为y=
∴①不正确;
②∵点E在双曲线y=的图象上,且E点的纵坐标为8,
∴32÷8=4,
∴点E(4,8),
∴②正确;
③∵sin∠COA==,
∴③正确;
④在Rt△CMA中,CM=8,AM=OA-OM=10-6=4,
∴AC===4,
∵OB?AC=160,
∴OB=8
∴AC+OB=12
∴④成立.
综上可知:②③④成立.
故答案为:A
3.B
【详解】如图,分别过点A、B作AN⊥x轴、BM⊥x轴;
∵∠AOB=90°,
∴∠BOM+∠AON=∠AON+∠OAN=90°,
∴∠BOM=∠OAN,
∵∠BMO=∠ANO=90°,
∴△BOM∽△OAN,
∴,
设设B(-m,),A(n,),
则BM=,AN=,OM=m,ON=n,
∴mn=,mn=;
∵∠AOB=90°,
∴tan∠OAB=①;
∵△BOM∽△OAN,
∴= ==②,
由①②知tan∠OAB=.
故正确选项为:B.
4.C
【解析】
如图:
∵点坐标为,
∴,
∴反比例函数解析式为,
∵,
∴为等腰直角三角形,
∴,
∵,
∴,
∵点和点关于直线对称,
∴,,
∴,,
∴轴,
∴点的坐标为,
∵,
∵,
整理得,
解得,(不符合体意,舍去),
∴的值为.
故选:.
5.B
【解析】
【详解】
解:如图过点A作AC⊥x轴于点C,过点B作BD⊥x轴于点D,
设B点坐标满足的函数解析式是
∵∠ACO=∠BDO=90°
∴∠AOC+∠0AC=90°,
∵∠AOB=90°,
∴∠AOC+∠BOD=90°,
∴.∠BOD=∠0AC,
∴△AOC∽△OBD,
∴
∵当A点在反比例函数y=-(x>0)的图象上移动,
解得:k=
∴B点坐标满足的函数解析式
故答案为:B.
6.C
【详解】
解:∵,,x轴⊥y轴,
∴OE=OF=1,∠FOE=90°,∠OEF=∠OFE=45°,
∴,
∴,
∵四边形ABCD为矩形,
∴∠A=90°,
∵轴,
∴∠DFE=∠OEF=45°,
∴∠ADF=45°,,
∴
∴D(4,1),
∴,解得,
故选:C.
7.B
【详解】
解:将函数的图象沿x轴向右平移1个单位长度,得到的图象所相应的函数表达式是,
故选:B.
8.B
【详解】
解:由题意可得A的横坐标为1×2=2,C的纵坐标为2×2=4,
∴B的坐标为(2,4),
∵B在反比例函数图象上,
∴
∴k=2×4=8,
故选B.
9.C
【详解】
解:A、反比例函数图象分布在第二、四象限,则k<0,所以A选项错误;
B、在每一象限,y随x的增大而增大,所以B选项错误;
C、矩形OABC面积为2,则|k|=2,而k<0,所以k=﹣2,所以C选项正确;
D、若图象上点B的坐标是(﹣2,1),则当x<﹣2时,y的取值范围是0<y<1,所以D选项错误.
故选C
10.C
【详解】
设反比例函数解析式为,
把点代入得:,
∴;
故答案选C.
11.1≤k≤4.
【详解】
解:当点A在双曲线上时,k=1
当点B在双曲线上时,k=4,∴双曲线与线段AB有公共点,则k的取值范围为1≤k≤4.
故答案为:1≤k≤4
12.9
【详解】
解:设,,则,
设,,
则,解得:,
在双曲线上,
,
故答案为:9.
13.
【详解】
过点D作DM⊥x轴于点M,
∵点D的坐标为(6,8),
∴OD=,
∵四边形OBCD是菱形,
∴OB=OD=10,
∴点B的坐标为:(10,0),
∵AB=AD,即A是BD的中点,
∴点A的坐标为:(,),即(8,4),
∵点A在反比例函数的图象上,
∴,
∴反比例函数的解析式为.
故答案为:.
14.3
【详解】
解:连结OC,过C作CD⊥x轴于D,BE⊥x轴于E,
由对称性可知:OA=OB,
∵△ABC是等边三角形,
∴OC⊥AB,
∵C(-3,3),
∴OC=3,
∴OB=OC=,
∵OD=CD=3,
∴∠DOC=∠DCO=45?,
∴∠EOB=90?-∠DOC=90?-45?=45?,
∴OE=BE,
在Rt△BEO中OE2+BE2=OB2=6,
∴OE=BE=,
∵点B在第三象限,
∴B(-,﹣),
把B点坐标代入y=,得到k=3,
故答案为:3.
15. 0、1
【详解】
解:当时,的纵坐标为,
的纵坐标和的纵坐标相同,则的横坐标为,
的横坐标和的横坐标相同,则的纵坐标为,
的纵坐标和的纵坐标相同,则的横坐标为,
的横坐标和的横坐标相同,则的纵坐标为,
的纵坐标和的纵坐标相同,则的横坐标为,
的横坐标和的横坐标相同,则的纵坐标为,
即当时,,,,,
,,,,,
,
;
点不能在轴上(此时找不到),即,
点不能在轴上(此时,在轴上,找不到),即,
解得:;
综上可得不可取0、1.
故答案为:;0、1.
16.观察:①增大;②上,1;③y≠1;探究:①m1+m2=0;②x<﹣1或0<x<1;0延伸:,左,1,下,2.
【详解】
操作:函数图象如图所示:
观察:①当x<0时,y随x的增大而增大;
②y=的图象是由y=﹣的图象向上平移1个单位长度得到.
③y的取值范围是y≠1.
故答案为:增大,上,1,y≠1;
探究:①y==1﹣,
∵A(m1,n1),B(m2,n2)在函数y=图象上,
∴n1=1﹣,n2=1﹣,
∵n1+n2=2,
∴=0,
∴=0,
∴m1+m2=0;
②由图象可知,
根据题意得:若y1>y2,则x的取值范围为x<﹣1或0<x<1,
故答案为x<﹣1或0<x<1;
延伸:函数y=的图象可以由反比例函数y=的图象向左平移1个单位,再向下平移2个单位得到,
故答案为,左,1,下,2.
17.(1);(2)见解析;(3)①见解析,②见解析
【详解】
解:(1)由图可知,点A为(3,2),则有
,
∴;
故答案为:;;
;
∵,
∵点A(3,2),B(,2),
∴,,
∴在如图的网格中可以画出的点有个,它们的坐标分别为
只需画出四个即可;
.
18.(1);(2)
【详解】
(1)根据题意得:
解得:,即点的坐标为
∵点在反比例函数的图象上,
∴
∴反比例函数的表达式为;
(2)如图,设平移后的直线与轴交于点,连接,
设平移后的解析式为,
∴
∵该直线平行直线,
∴
∵的面积为36,
∴
由对称性可知:,
∴
∴
∴
∴平移后的直线的函数表达式为.
_21?????????è?????(www.21cnjy.com)_
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
