二次函数综合题
图片预览


文档简介
(共12张PPT)
二次函数综合题
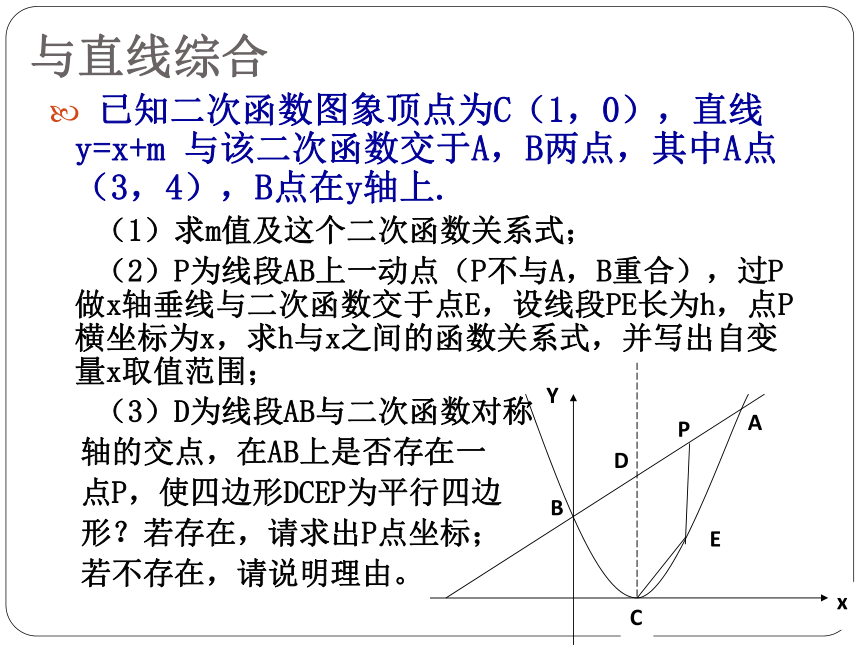
与直线综合
已知二次函数图象顶点为C(1,0),直线 y=x+m 与该二次函数交于A,B两点,其中A点(3,4),B点在y轴上.
(1)求m值及这个二次函数关系式;
(2)P为线段AB上一动点(P不与A,B重合),过P做x轴垂线与二次函数交于点E,设线段PE长为h,点P横坐标为x,求h与x之间的函数关系式,并写出自变量x取值范围;
(3)D为线段AB与二次函数对称
轴的交点,在AB上是否存在一
点P,使四边形DCEP为平行四边
形?若存在,请求出P点坐标;
若不存在,请说明理由。
x
D
Y
A
C
E
P
B
抛物线y=x +4x+3交x轴于A、B两点,交y轴于
点C,抛物线的对称轴交x轴于点E.
(1)求抛物线的对称轴及点A的坐标;
(2)在平面直角坐标系xoy 中是否存在点P,与A、B、C三点构成一个平行四边形?若存在,请写出点P的坐标;若不存在,请说明理由;
(3)连结CA与抛物线的对称轴
交于点D,在抛物线上是否存在
点M,使得直线CM把四边形DEOC
分成面积相等的两部分?若存在,
请求出直线CM的解析式;若不存
在,请说明理由.
O
D
B
C
A
E
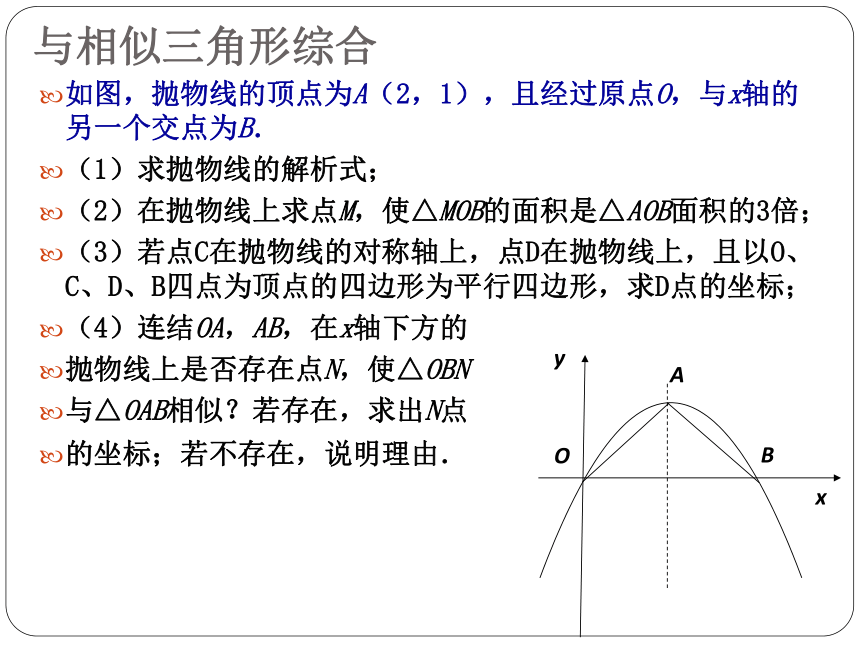
与相似三角形综合
如图,抛物线的顶点为A(2,1),且经过原点O,与x轴的另一个交点为B.
(1)求抛物线的解析式;
(2)在抛物线上求点M,使△MOB的面积是△AOB面积的3倍;
(3)若点C在抛物线的对称轴上,点D在抛物线上,且以O、C、D、B四点为顶点的四边形为平行四边形,求D点的坐标;
(4)连结OA,AB,在x轴下方的
抛物线上是否存在点N,使△OBN
与△OAB相似?若存在,求出N点
的坐标;若不存在,说明理由.
y
x
O
A
B
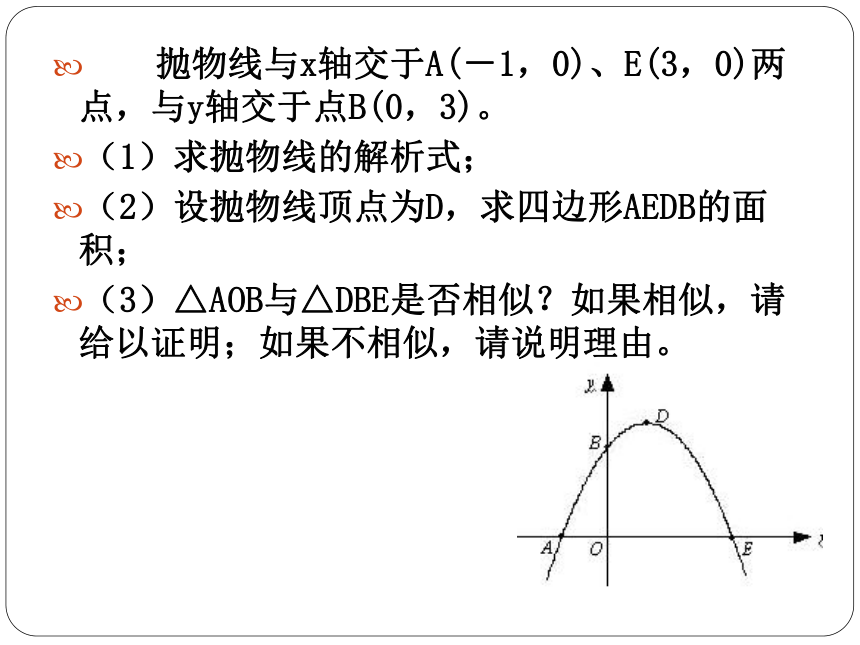
抛物线与x轴交于A(-1,0)、E(3,0)两点,与y轴交于点B(0,3)。
(1)求抛物线的解析式;
(2)设抛物线顶点为D,求四边形AEDB的面积;
(3)△AOB与△DBE是否相似?如果相似,请给以证明;如果不相似,请说明理由。
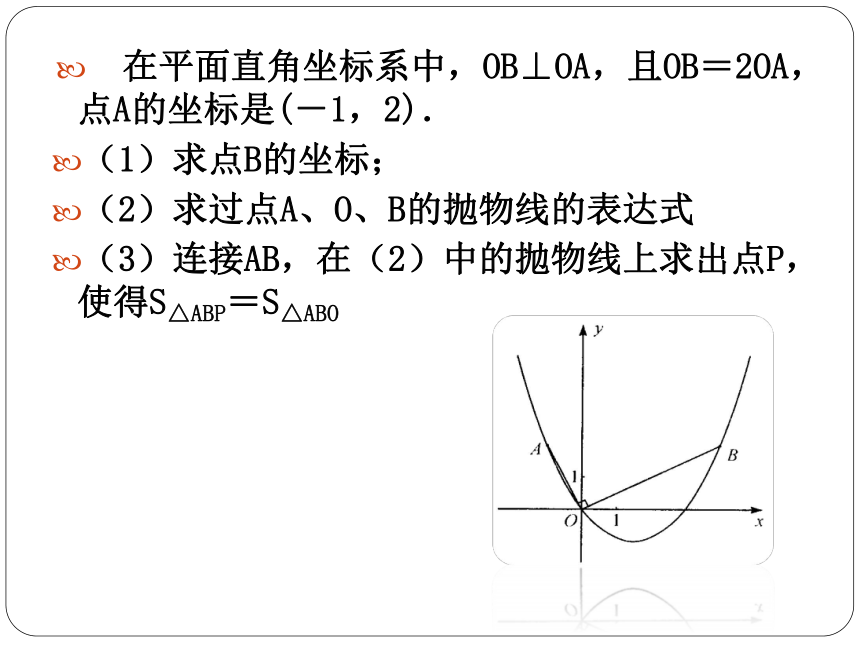
在平面直角坐标系中,OB⊥OA,且OB=2OA,点A的坐标是(-1,2).
(1)求点B的坐标;
(2)求过点A、O、B的抛物线的表达式
(3)连接AB,在(2)中的抛物线上求出点P,使得S△ABP=S△ABO
已知抛物线y=ax +bx+c经过 及原点.
(1)求抛物线的解析式.
(2)过点P作平行于x轴的直线PC交y轴于点C,在抛物线对称轴右侧且位于直线PC下方的抛物线上,任取一点Q,过点Q作直线QA平行于y轴交x轴于A点,交直线PC于B点,直线QA与直线PC及两坐标轴围成矩形OABC.是否存在点Q,使得△OPC与△PQB相似?若存在,求出Q点的坐标;若不存在,说明理由.
(3)如果符合(2)中的Q点在x
轴的上方,连结OQ,矩形OABC
内的四个三角形△OPC,△PQB,
△OPQ,△OQA之间存在怎样的
关系?为什么?
在平面直角坐标系xoy中,已知二次函数y=ax +bx+c的图象与x轴交于A,B两点(点A在点B的左边),与y轴交于点C,其顶点的横坐标为1,且过点(2,3)和(-3,-12).
(1)求此二次函数的表达式.
(2)若直线l:y=kx(k≠0)与线段BC交于点D(不与点B,C重合),则是否存在这样的直线l,使得以B,O,D为顶点的三角形与△ABC相似?若存在,求出该直线的函数表达式及点D的坐标;若不存在,请说明理由;
(3)若点P是位于该二次函数对称轴
右边图象上不与顶点重合的任意一点,
试比较锐角∠PCO与∠ACO的大小(不
必证明),并写出此时点P的横坐标xp
的取值范围.
y
C
x
B
A
O
如图所示,已知抛物线y=x -1与x轴交于A、B两点,与y轴交于点C.
(1)求A、B、C三点的坐标.
(2)过点A作AP∥CB交抛物线于点P,求四边形ACBP的面积.
(3)在x轴上方的抛物线上是否存在一点M,过M作MG⊥x轴于点G,使以A、M、G三点为顶点的三角形与PCA相似.若存在,请求出M点的坐标;否则,请说明理由.
C
B
A
P
y
与圆综合
在平面直角坐标系 xoy中,半径为1的圆的圆心O在坐标原点,且与两坐标轴分别交于 A、B、C、D四点.抛物线y=ax +bx+c与y轴交于点D ,与直线 y=x交于点M、N ,且MA、NC 分别与圆O 相切于点A和点C.
(1)求抛物线的解析式;
(2)抛物线的对称轴交x 轴于
点E,连结DE,并延长DE交圆O于F,
求EF的长.
(3)过点B作圆O的切线交DC的
延长线于点P,判断点P是否在
抛物线上,说明理由.
O
x
y
N
C
D
E
F
B
M
A
如图,在直角坐标系xoy中,A、B是x轴上的两点,以AB为直径的圆交y轴于C,设过A、B、C三点的抛物线的解析式为y=x2-mx+n,方程x2-mx+n=0的两根倒数和为-2.
(1)求n的值;
(2)求此抛物线的解析式;
(3)设平行于x轴的直线交此抛物线于E、F两点,问是否存在此线段EF为直径的圆恰好
与x轴相切,若存在,求出此圆的
半径;若不存在,说明理由.
再见
二次函数综合题
与直线综合
已知二次函数图象顶点为C(1,0),直线 y=x+m 与该二次函数交于A,B两点,其中A点(3,4),B点在y轴上.
(1)求m值及这个二次函数关系式;
(2)P为线段AB上一动点(P不与A,B重合),过P做x轴垂线与二次函数交于点E,设线段PE长为h,点P横坐标为x,求h与x之间的函数关系式,并写出自变量x取值范围;
(3)D为线段AB与二次函数对称
轴的交点,在AB上是否存在一
点P,使四边形DCEP为平行四边
形?若存在,请求出P点坐标;
若不存在,请说明理由。
x
D
Y
A
C
E
P
B
抛物线y=x +4x+3交x轴于A、B两点,交y轴于
点C,抛物线的对称轴交x轴于点E.
(1)求抛物线的对称轴及点A的坐标;
(2)在平面直角坐标系xoy 中是否存在点P,与A、B、C三点构成一个平行四边形?若存在,请写出点P的坐标;若不存在,请说明理由;
(3)连结CA与抛物线的对称轴
交于点D,在抛物线上是否存在
点M,使得直线CM把四边形DEOC
分成面积相等的两部分?若存在,
请求出直线CM的解析式;若不存
在,请说明理由.
O
D
B
C
A
E
与相似三角形综合
如图,抛物线的顶点为A(2,1),且经过原点O,与x轴的另一个交点为B.
(1)求抛物线的解析式;
(2)在抛物线上求点M,使△MOB的面积是△AOB面积的3倍;
(3)若点C在抛物线的对称轴上,点D在抛物线上,且以O、C、D、B四点为顶点的四边形为平行四边形,求D点的坐标;
(4)连结OA,AB,在x轴下方的
抛物线上是否存在点N,使△OBN
与△OAB相似?若存在,求出N点
的坐标;若不存在,说明理由.
y
x
O
A
B
抛物线与x轴交于A(-1,0)、E(3,0)两点,与y轴交于点B(0,3)。
(1)求抛物线的解析式;
(2)设抛物线顶点为D,求四边形AEDB的面积;
(3)△AOB与△DBE是否相似?如果相似,请给以证明;如果不相似,请说明理由。
在平面直角坐标系中,OB⊥OA,且OB=2OA,点A的坐标是(-1,2).
(1)求点B的坐标;
(2)求过点A、O、B的抛物线的表达式
(3)连接AB,在(2)中的抛物线上求出点P,使得S△ABP=S△ABO
已知抛物线y=ax +bx+c经过 及原点.
(1)求抛物线的解析式.
(2)过点P作平行于x轴的直线PC交y轴于点C,在抛物线对称轴右侧且位于直线PC下方的抛物线上,任取一点Q,过点Q作直线QA平行于y轴交x轴于A点,交直线PC于B点,直线QA与直线PC及两坐标轴围成矩形OABC.是否存在点Q,使得△OPC与△PQB相似?若存在,求出Q点的坐标;若不存在,说明理由.
(3)如果符合(2)中的Q点在x
轴的上方,连结OQ,矩形OABC
内的四个三角形△OPC,△PQB,
△OPQ,△OQA之间存在怎样的
关系?为什么?
在平面直角坐标系xoy中,已知二次函数y=ax +bx+c的图象与x轴交于A,B两点(点A在点B的左边),与y轴交于点C,其顶点的横坐标为1,且过点(2,3)和(-3,-12).
(1)求此二次函数的表达式.
(2)若直线l:y=kx(k≠0)与线段BC交于点D(不与点B,C重合),则是否存在这样的直线l,使得以B,O,D为顶点的三角形与△ABC相似?若存在,求出该直线的函数表达式及点D的坐标;若不存在,请说明理由;
(3)若点P是位于该二次函数对称轴
右边图象上不与顶点重合的任意一点,
试比较锐角∠PCO与∠ACO的大小(不
必证明),并写出此时点P的横坐标xp
的取值范围.
y
C
x
B
A
O
如图所示,已知抛物线y=x -1与x轴交于A、B两点,与y轴交于点C.
(1)求A、B、C三点的坐标.
(2)过点A作AP∥CB交抛物线于点P,求四边形ACBP的面积.
(3)在x轴上方的抛物线上是否存在一点M,过M作MG⊥x轴于点G,使以A、M、G三点为顶点的三角形与PCA相似.若存在,请求出M点的坐标;否则,请说明理由.
C
B
A
P
y
与圆综合
在平面直角坐标系 xoy中,半径为1的圆的圆心O在坐标原点,且与两坐标轴分别交于 A、B、C、D四点.抛物线y=ax +bx+c与y轴交于点D ,与直线 y=x交于点M、N ,且MA、NC 分别与圆O 相切于点A和点C.
(1)求抛物线的解析式;
(2)抛物线的对称轴交x 轴于
点E,连结DE,并延长DE交圆O于F,
求EF的长.
(3)过点B作圆O的切线交DC的
延长线于点P,判断点P是否在
抛物线上,说明理由.
O
x
y
N
C
D
E
F
B
M
A
如图,在直角坐标系xoy中,A、B是x轴上的两点,以AB为直径的圆交y轴于C,设过A、B、C三点的抛物线的解析式为y=x2-mx+n,方程x2-mx+n=0的两根倒数和为-2.
(1)求n的值;
(2)求此抛物线的解析式;
(3)设平行于x轴的直线交此抛物线于E、F两点,问是否存在此线段EF为直径的圆恰好
与x轴相切,若存在,求出此圆的
半径;若不存在,说明理由.
再见
同课章节目录
