2.3二次函数的性质

(共34张PPT)
(1).每个图象与x轴有几个交点？
二次函数与一元二次方程
二次函数y=x2+2x,y=x2-2x+1,y=x2-2x+2的图象如图所示.
y=x2+2x
y=x2-2x+1
y=x2-2x+2
(3你能求出图象与x轴交点的坐标
(2).一元二次方程x +2x=0,x -2x+1=0有几个根 验证一下一元二次方程x -2x+2=0有根吗
2
2
2
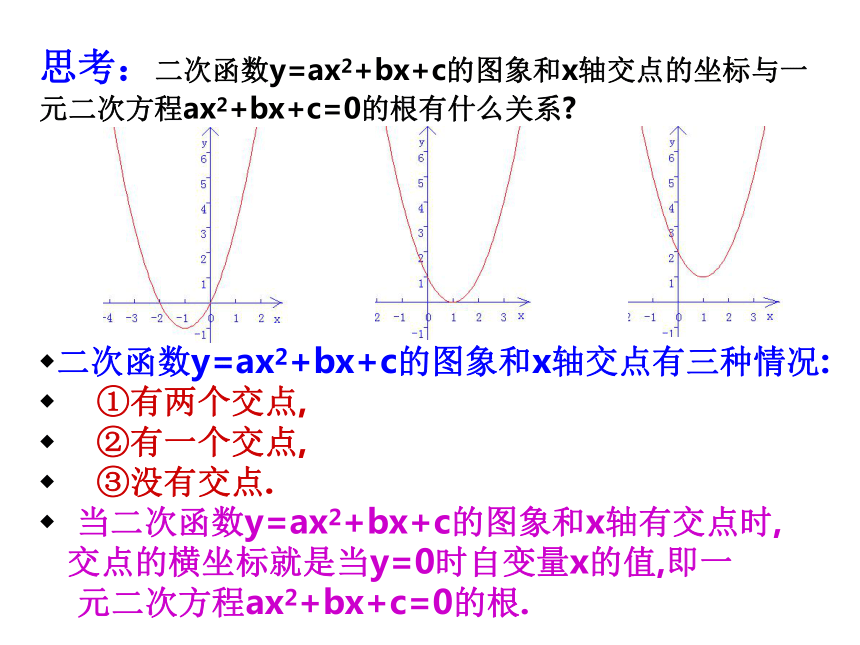
二次函数y=ax2+bx+c的图象和x轴交点有三种情况:
①有两个交点,
②有一个交点,
③没有交点.
当二次函数y=ax2+bx+c的图象和x轴有交点时,
交点的横坐标就是当y=0时自变量x的值,即一
元二次方程ax2+bx+c=0的根.
思考：二次函数y=ax2+bx+c的图象和x轴交点的坐标与一元二次方程ax2+bx+c=0的根有什么关系
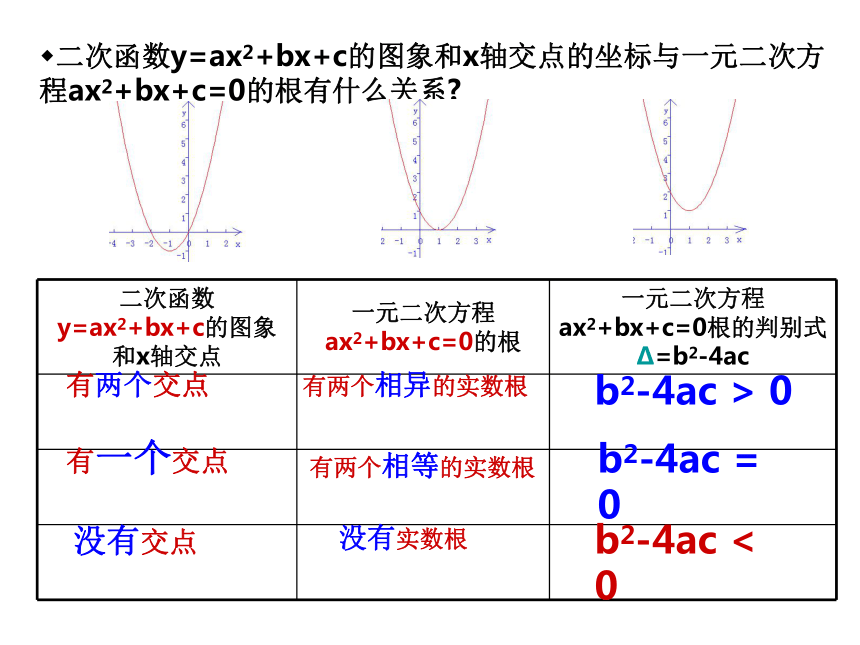
二次函数y=ax2+bx+c的图象和x轴交点的坐标与一元二次方程ax2+bx+c=0的根有什么关系
二次函数y=ax2+bx+c的图象和x轴交点 一元二次方程ax2+bx+c=0的根 一元二次方程ax2+bx+c=0根的判别式Δ=b2-4ac
有两个交点
有两个相异的实数根
b2-4ac > 0
有一个交点
有两个相等的实数根
b2-4ac = 0
没有交点
没有实数根
b2-4ac < 0
求二次函数图象y=x2-3x+2与x轴的交点A、B的坐标。
解：∵A、B在x轴上，
∴它们的纵坐标为0，
∴令y=0，则x2-3x+2=0
解得：x1=1，x2=2；
∴A（1，0） ， B（2，0）
你发现方程 的解x1、x2与A、B的坐标有什么联系？
x2-3x+2=0
举例:
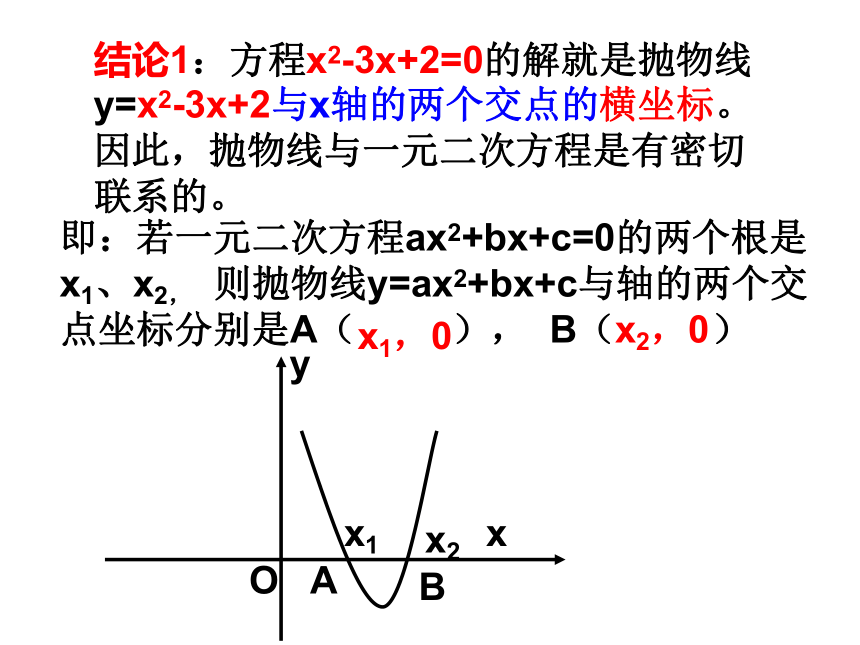
结论1：方程x2-3x+2=0的解就是抛物线y=x2-3x+2与x轴的两个交点的横坐标。因此，抛物线与一元二次方程是有密切联系的。
即：若一元二次方程ax2+bx+c=0的两个根是x1、x2， 则抛物线y=ax2+bx+c与轴的两个交点坐标分别是A（ ）， B（ ）
x1，0
x2，0
x
O
A
B
x1
x2
y
已知抛物线经过点(3,0),(2,-3),并以直线x=0为对称轴 (1)求这条抛物线的解析式. (2)求出这个二次函数的最大值或最小值. (3)在此抛物线上有两点A(x1,y1),B(x2,y2),且x1>x2>0,试比较y1与y2的大小.
1、二次函数y=ax2+bx+c(a≠0)的图象如图所示，
则a、b、c的符号为__________.　　　　　　
y
x
o
2、已知二次函数的图像如图所示，下列结论：
⑴a+b+c﹤0 ⑵a-b+c﹥0 ⑶abc ﹥0 ⑷b=2a
其中正确的结论的个数是（ ）A 1个 B 2个 C 3个 D 4个
D
x
-1
1
0
y
要点：寻求思路时，要着重观察抛物线的开口方向，对称轴，顶点的位置，抛物线与x轴、y轴的交点的位置，注意运用数形结合的思想。
3、下列函数何时有最大值或最小值，并求出最大值或最小值
⑴ y=2x2-8x-3 ⑵ y=-5x２＋３√２x- 4
4、二次函数y=x2＋bx+8的图像顶点在x轴的负半轴上， 那么b等于多少？
3,如图直线l经过点A(4,0)和B(0,4)两点,它与二次函数y=ax2的图像在第一象限内相交于P点,若△AOP的面积为4.5,求二次函数的解析式.
A
B
P
O
x
y
4,将抛物线y=x2向下平移后,使它的顶点C与它在x轴上的两个交点A,B组成等边三角形ABC,求此抛物线的解析式.
小试牛刀
如图，在ΔABC中，AB=8cm，BC=6cm，∠B＝90°，
点P从点A开始沿AB边向点B以2厘米／秒的速度移动，
点Q从点B开始沿BC边向点C以1厘米／秒的速度
移动，如果P,Q分别从A,B同时出发，
几秒后ΔPBQ的面积最大？
最大面积是多少？
A
B
C
P
Q
解：根据题意，设经过x秒后ΔPBQ的面积y最大,则：
AP=2x cm PB=（8-2x ） cm
QB=x cm
则 y=1/2 x（8-2x）
=-x2 +4x
=-（x2 -4x +4 -4）
= -（x - 2）2 + 4
所以，当P、Q同时运动2秒后ΔPBQ的面积y最大
最大面积是 4 cm2
（0A
B
C
P
Q
问题5:如图，等腰Rt△ABC的直角边AB＝２，点P、Q分别从A、C两点同时出发，以相等的速度作直线运动，已知点P沿射线AB运动，点Q沿边BC的延长线运动，PQ与直线相交于点D。
(1)设 AP的长为x，△PCQ的面积为S，求出S关于x的函数关系式；
(2)当AP的长为何值时，S△PCQ= S△ABC
解：（１）∵P、Q分别从A、C两点同时出发，速度相等
∴AP=CQ=x
当P在线段AB上时
S△PCQ＝
CQ PB
=
AP PB
即S＝ 　 (0当P在线段AB的延长线上时
S△PCQ＝
即S＝　 (x>2）
(2)当S△PCQ＝S△ABC时，有
＝２
此方程无解
②　 ＝２
　　　　　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　
∴ x1=1+ , x2=1－ (舍去)
∴当AP长为1+ 时，S△PCQ＝S△ABC
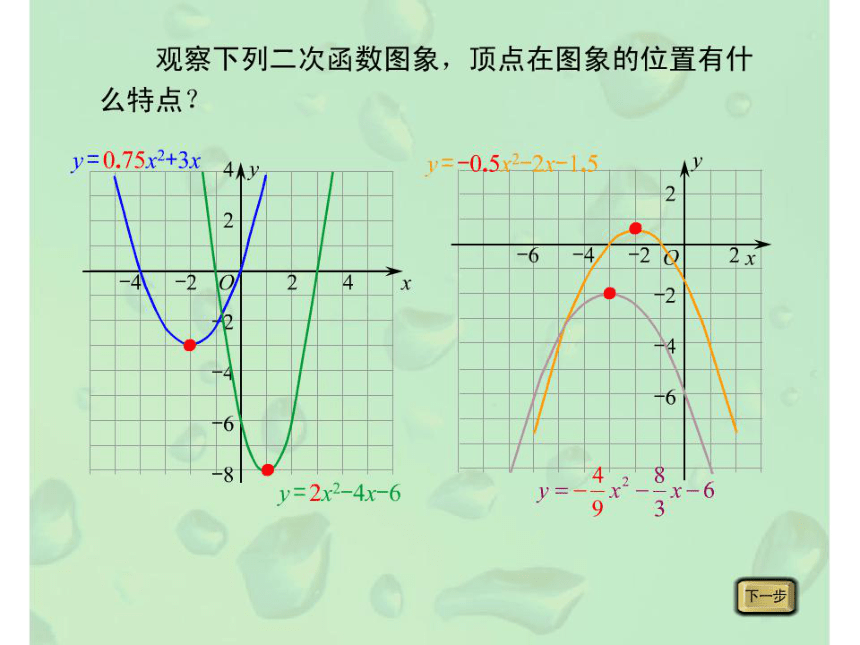
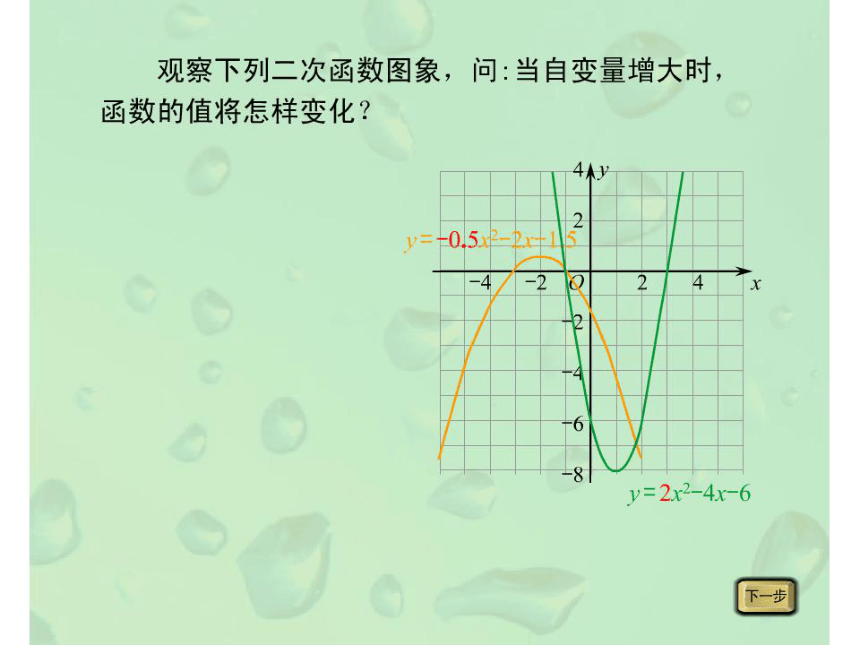
1、你能正确地说出二次函数的性质吗？
2、你能用“五点法”快速地画出二次函数的图象吗？你能利用函数图象回答有关性质吗？