2.4二次函数的应用②

(共11张PPT)
如何运用二次函数求实际问题中的最大值或最小值
复习思考
首先应当求出函数解析式和自变量的取值范围，然后通过配方变形，或利用公式求它的最大值或最小值。
注意：由此求得的最大值或最小值对应的自变量的值必须在自变量的取值范围内 。
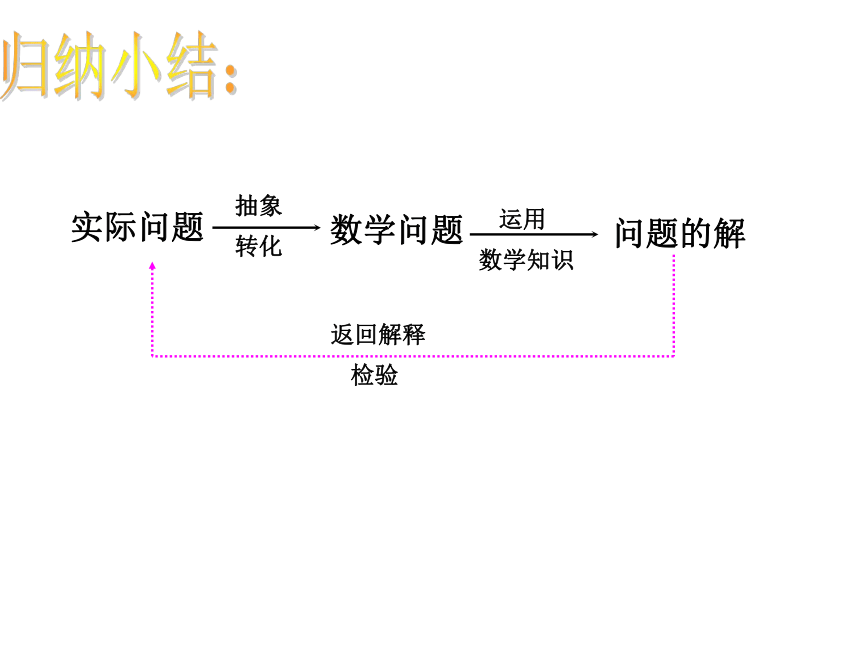
实际问题
抽象
转化
数学问题
运用
数学知识
问题的解
返回解释
检验
1、某广告公司设计一幅周长为12m的矩形广告牌，
广告设计费为每平方米1000元，设矩形一边长为
X(m)，面积为S(m2)。
(1)、求出S与x之间的函数关系式，并确定自
变量的取值范围。
(2)、请你设计一个方案，使获得的设计费最多。
1、通过这节课的学习活动你有哪些收获？
2、对这节课的学习，你还有什么想法吗？
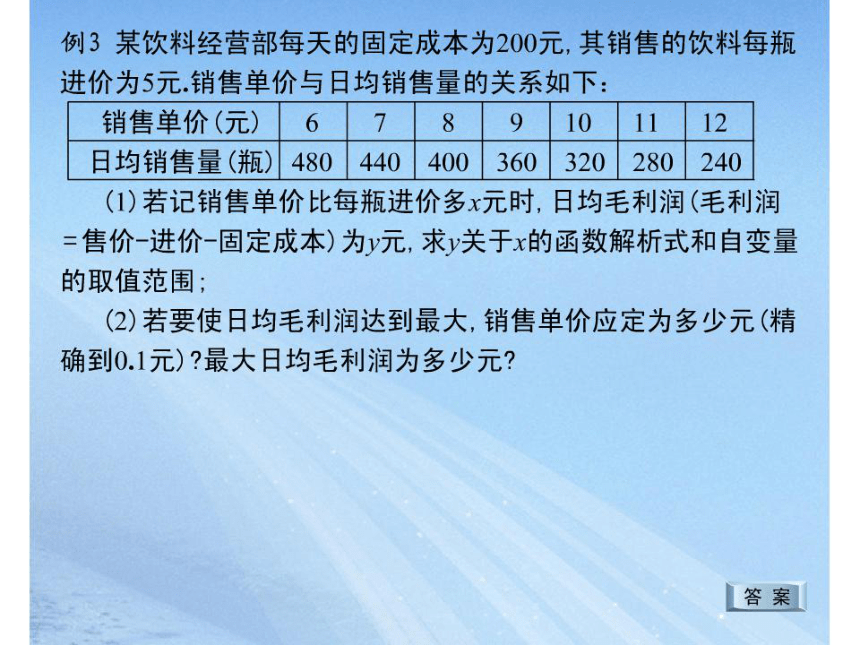
例3某饮料经营部每天的固定成本为200元,其销售的饮料每瓶
进价为5元销售单价与日均销售量的关系如下:
销售单价(元)6789101112
日均销售量(瓶)480440400360320280240
(2)若要使日均毛利润达到最大,销售单价应定为多少元(精
确到0.1元) 最大日均毛利润为多少元
解:(2)由第(1)题,得y=-40(x-)2+1490(013
当x=时,函数达到最大值1490
而x=-满足0当销售单价定为115元时,日均毛利润最大,为1490元
答:若要使日均毛利润达到最大,销售单价应定为11.5元
最大日均毛利润为1490元
例2如图,B船位于A船正东26km处现在A,B两船同时出发
A船以12kmh的速度朝正北方向行驶,B船以5km/h的速度朝
正西方向行驶何时两船相距最近 最近距离是多少
解:设经过t(h)后,A,B两船分别到达A,B
处,则两船之间的距离为
AB=√AB2+A2=√(26-5)2+(12)
169t2-260t+676
(13t-10)2+576(t>0)
当13-10=0,即=10时
(13-10)2+576有最小值576
B
所以当=10h时,AB=576=24(km)
课内练
j积种植的株数构成
每平方米种植4株
单株产量为2
培条件,每平方
每增加1株,单株产量減
每平方米种植多少株时,能获
的产量 最
大的产量为多
解:设每平方米种植株,产量为y(kg),由题意得
(2
(3
)2+9
每平方米种植6株时,能获得最大产量,最大产