浙教版数学 八年级下册5章 特殊平行四边形专题培优 :一次函数中的特殊四边形(Word版 含解析)
文档属性
| 名称 | 浙教版数学 八年级下册5章 特殊平行四边形专题培优 :一次函数中的特殊四边形(Word版 含解析) |
|
|
| 格式 | zip | ||
| 文件大小 | 655.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-25 00:00:00 | ||
图片预览


文档简介
浙教版数学
八年级下册4-5章专题培优
一次函数中的特殊四边形
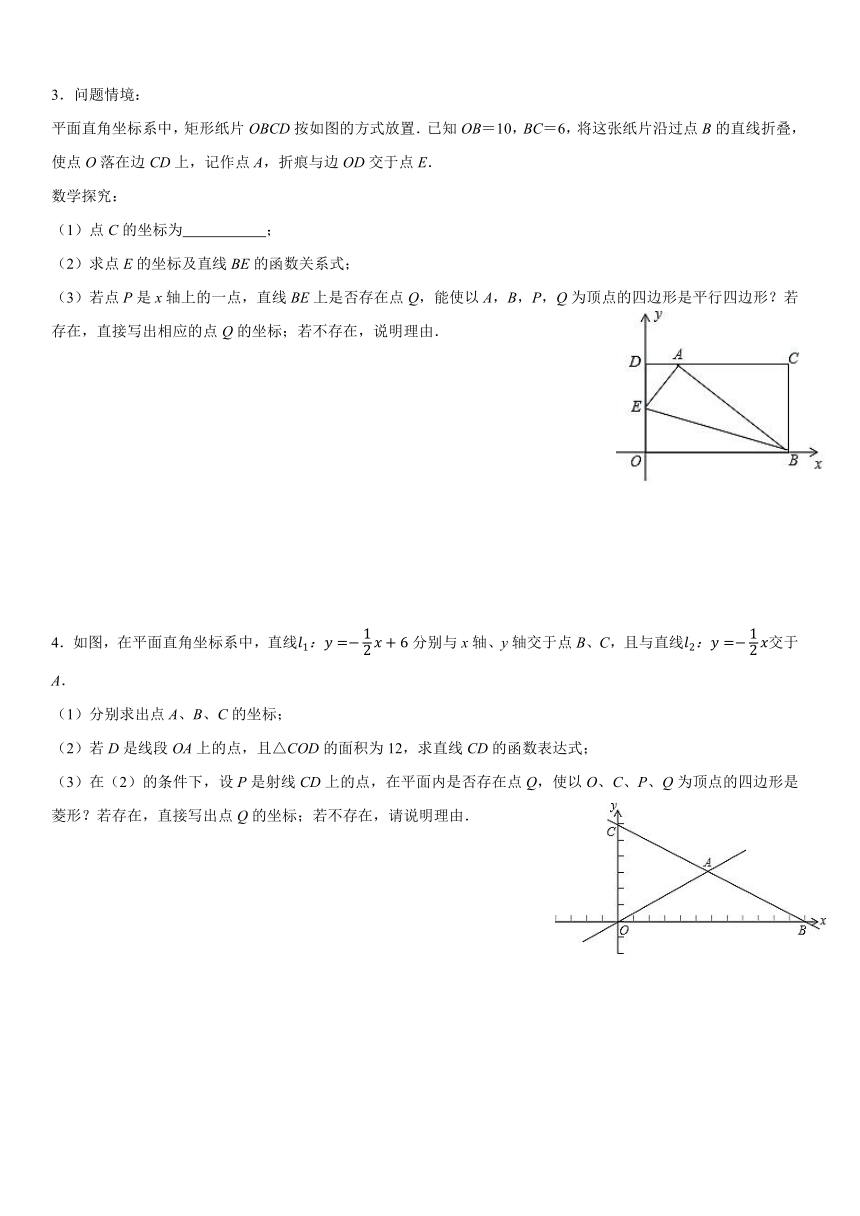
1.已知,如图,在平面直角坐标系xOy中,直线l1:y=x+3分别交x轴、y轴于点A、B两点,直线l2:y=﹣3x过原点且与直线l1相交于C,点P为y轴上一动点.
(1)求点C的坐标;
(2)求出△BCO的面积;
(3)当PA+PC的值最小时,求此时点P的坐标.
2.已知,如图,在平面直角坐标系xoy中,直线l1:y=x+3分别交x轴、y轴于点A、B两点,直线l2:y=﹣3x过原点且与直线l1相交于C,点P为y轴上一动点.
(1)求点C的坐标;
(2)在平面坐标系中是否存在点M,使以A、O、C、M为顶点的四边形为平行四边形.若存在,求出点M的坐标;若不存在,请说明理由;
(3)当PA+PC的值最小时,求此时点P的坐标,并求PA+PC的最小值.
3.问题情境:
平面直角坐标系中,矩形纸片OBCD按如图的方式放置.已知OB=10,BC=6,将这张纸片沿过点B的直线折叠,使点O落在边CD上,记作点A,折痕与边OD交于点E.
数学探究:
(1)点C的坐标为
;
(2)求点E的坐标及直线BE的函数关系式;
(3)若点P是x轴上的一点,直线BE上是否存在点Q,能使以A,B,P,Q为顶点的四边形是平行四边形?若存在,直接写出相应的点Q的坐标;若不存在,说明理由.
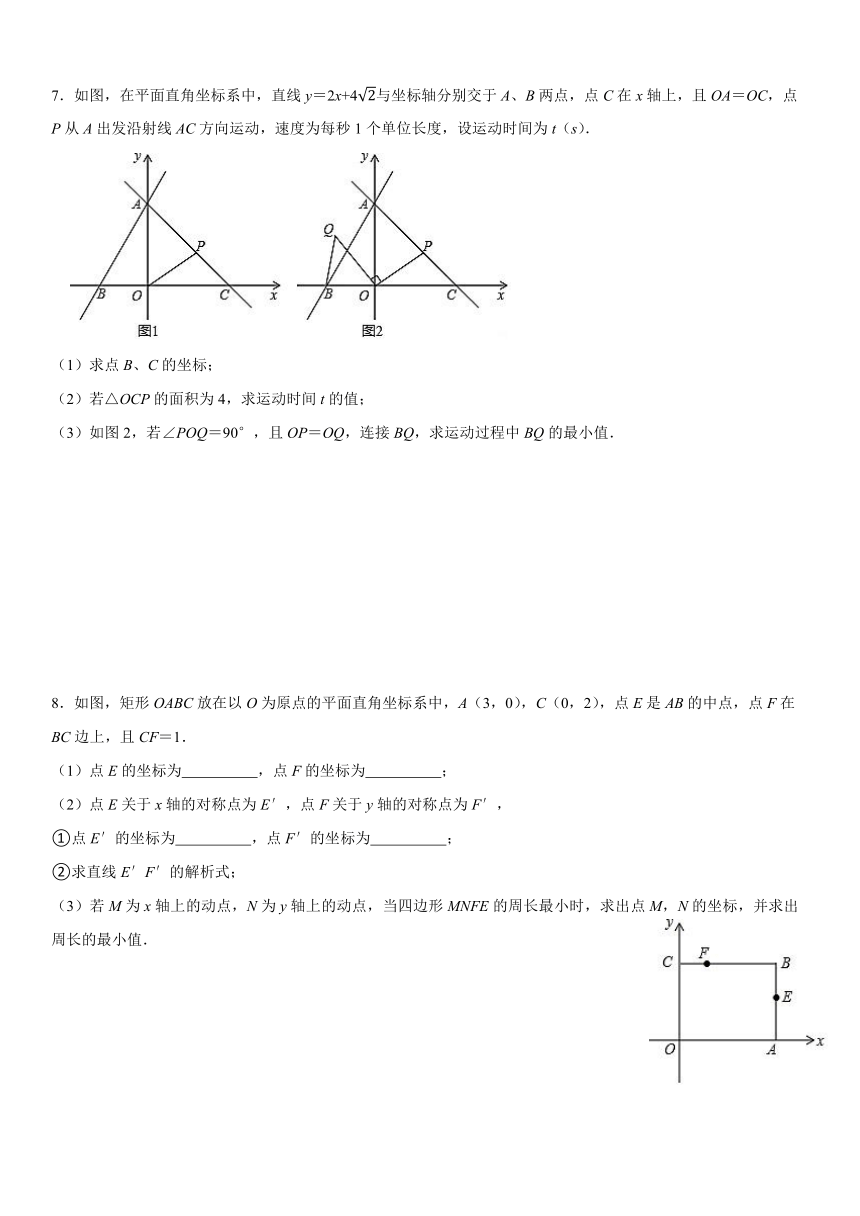
4.如图,在平面直角坐标系中,直线分别与x轴、y轴交于点B、C,且与直线交于A.
(1)分别求出点A、B、C的坐标;
(2)若D是线段OA上的点,且△COD的面积为12,求直线CD的函数表达式;
(3)在(2)的条件下,设P是射线CD上的点,在平面内是否存在点Q,使以O、C、P、Q为顶点的四边形是菱形?若存在,直接写出点Q的坐标;若不存在,请说明理由.
5.如图,在直角坐标系中,OA=3,OC=4,点B是y轴上一动点,以AC为对角线作平行四边形ABCD.
(1)求直线AC的函数解析式;
(2)设点B(0,m),记平行四边形ABCD的面积为S,请写出S与m的函数关系式,并求当BD取得最小值时的S的值;
(3)当点B在y轴上运动,在使得平行四边形ABCD是菱形的同时,在x轴取一点P,使得△PAB是等腰三角形,请直接写出点P的坐标.
6.已知:如图,已知直线AB的函数解析式为y=﹣2x+8,与x轴交于点A,与y轴交于点B.
(1)求A、B两点的坐标;
(2)若点P(m,n)为线段AB上的一个动点(与A、B不重合),作PE⊥x轴于点E,PF⊥y轴于点F,连接EF,问:
①若△PAO的面积为S,求S关于m的函数关系式,并写出m的取值范围;
②是否存在点P,使EF的值最小?若存在,求出EF的最小值;若不存在,请说明理由.
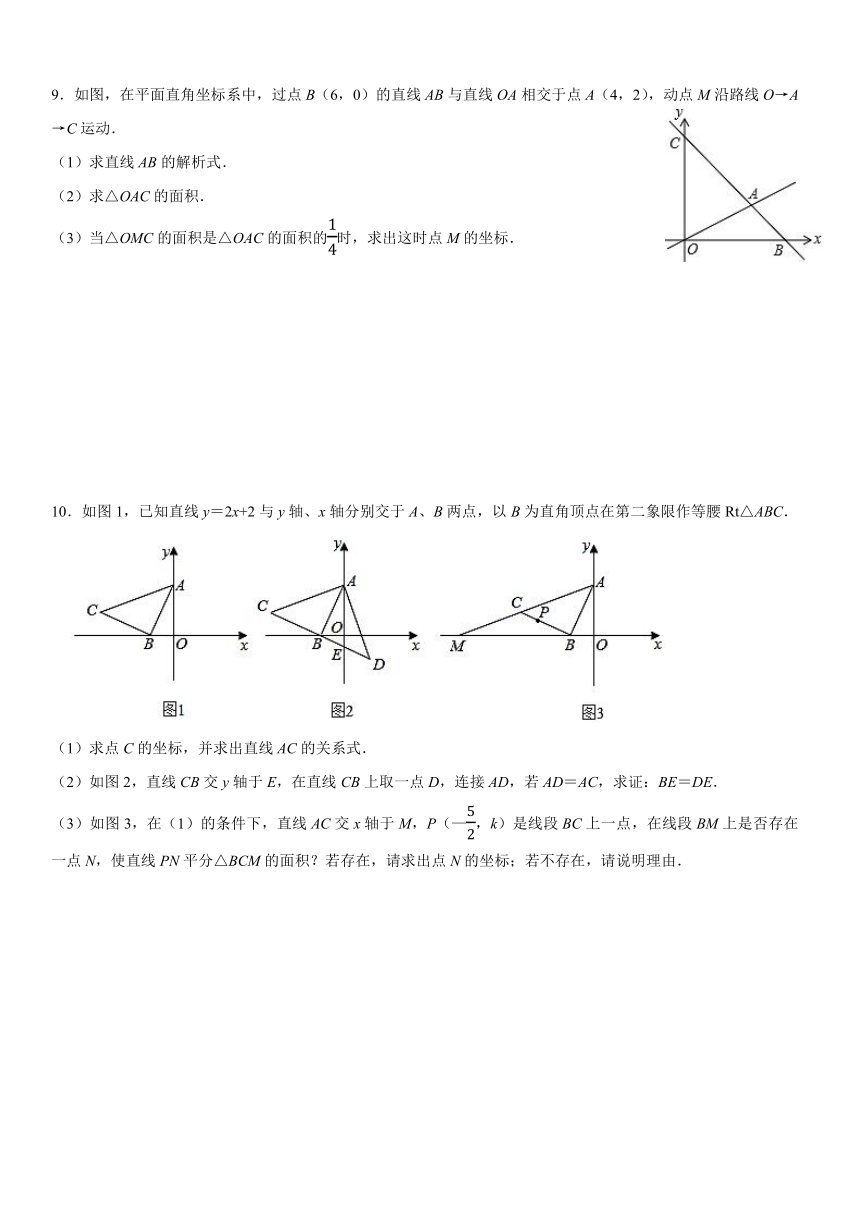
7.如图,在平面直角坐标系中,直线y=2x+4与坐标轴分别交于A、B两点,点C在x轴上,且OA=OC,点P从A出发沿射线AC方向运动,速度为每秒1个单位长度,设运动时间为t(s).
(1)求点B、C的坐标;
(2)若△OCP的面积为4,求运动时间t的值;
(3)如图2,若∠POQ=90°,且OP=OQ,连接BQ,求运动过程中BQ的最小值.
8.如图,矩形OABC放在以O为原点的平面直角坐标系中,A(3,0),C(0,2),点E是AB的中点,点F在BC边上,且CF=1.
(1)点E的坐标为
,点F的坐标为
;
(2)点E关于x轴的对称点为E′,点F关于y轴的对称点为F′,
①点E′的坐标为
,点F′的坐标为
;
②求直线E′F′的解析式;
(3)若M为x轴上的动点,N为y轴上的动点,当四边形MNFE的周长最小时,求出点M,N的坐标,并求出周长的最小值.
9.如图,在平面直角坐标系中,过点B(6,0)的直线AB与直线OA相交于点A(4,2),动点M沿路线O→A→C运动.
(1)求直线AB的解析式.
(2)求△OAC的面积.
(3)当△OMC的面积是△OAC的面积的时,求出这时点M的坐标.
10.如图1,已知直线y=2x+2与y轴、x轴分别交于A、B两点,以B为直角顶点在第二象限作等腰Rt△ABC.
(1)求点C的坐标,并求出直线AC的关系式.
(2)如图2,直线CB交y轴于E,在直线CB上取一点D,连接AD,若AD=AC,求证:BE=DE.
(3)如图3,在(1)的条件下,直线AC交x轴于M,P(—,k)是线段BC上一点,在线段BM上是否存在一点N,使直线PN平分△BCM的面积?若存在,请求出点N的坐标;若不存在,请说明理由.
11.【背景知识】研究平面直角坐标系,我们可以发现一条重要的规律:若平面直角坐标系上有两个不同的点A(xA,yA)、B(xB,yB),则线段AB的中点坐标可以表示为(,).
【简单应用】如图1,直线AB与y轴交于点A(0,3),与x轴交于点B(4,0),过原点O的直线L将△ABO分成面积相等的两部分,请求出直线L的解析式;
【探究升级】小明发现“若四边形一条对角线平分四边形的面积,则这条对角线必经过另一条对角线的中点”
如图2,在四边形ABCD中,对角线AC、BD相交于点O,S△ABD=S△BCD.试说明AO=CO;
【综合运用】如图3,在平面直角坐标系中A(1,4),B(3,﹣2),C(2m,﹣m+5),若OC恰好平分四边形OACB的面积,求点C的坐标.
12.如图,四边形ABCD是正方形,E是边AB上一点,连接DE,将直线DE绕点D逆时针旋转90°,交BC的延长线于点F
(1)如图1,求证:DE=DF;
(2)如图2,连接EF,若D关于直线EF的对称点为H,连接CH,过点H作PH⊥CH交AB于点P,求证:E是AP的中点;
(3)如图3,在(2)的条件下,连接AC交EF于点G,连接BG、BH,若BG=2,AB=6,求线段PH的长.
13.如图,四边形ABCD是正方形,E是边AB上一点,连接DE,直线DE绕着点D逆时针旋转90°,交BC的延长线于点F.
(1)如图1,求证:DE=DF;
(2)如图2,连接EF,若D关于直线EF的对称点为H,连接CH,过点H作PH⊥CH交AB于点P,求证:E为AP中点;
(3)如图3,在(2)的条件下,连接AC交EF于点G,连接BG,BH,若BG=,AB=3,求线段PH的长.
14.如图1,在△ABC中,∠ACB为锐角,点D为射线BC上一点,联结AD,以AD为一边且在AD的右侧作正方形ADEF.
(1)如果AB=AC,∠BAC=90°,
①当点D在线段BC上时(与点B不重合),如图2,将△ABD绕A点逆时针旋转90°,所得到的三角形为
,线段CF、BD所在直线的位置关系为
,线段CF、BD的数量关系为
;
②当点D在线段BC的延长线上时,如图3,①中的结论是否仍然成立,并说明理由;
(2)如果AB≠AC,∠BAC是锐角,点D在线段BC上,当∠ACB满足什么条件时,CF⊥BC(点C、F不重合),并说明理由.
15.如图,正方形ABCD中,AC是对角线,今有较大的直角三角板,一边始终经过点B,直角顶点P在射线AC上移动,另一边交DC于Q.
(1)如图1,当点Q在DC边上时,猜想并写出PB与PQ所满足的数量关系;并加以证明;
(2)如图2,当点Q落在DC的延长线上时,猜想并写出PB与PQ满足的数量关系,请证明你的猜想.
浙教版数学
八年级下册4-5章专题培优
一次函数中的特殊四边形
参考答案与试题解析
一.解答题(共15小题)
1.已知,如图,在平面直角坐标系xOy中,直线l1:y=x+3分别交x轴、y轴于点A、B两点,直线l2:y=﹣3x过原点且与直线l1相交于C,点P为y轴上一动点.
(1)求点C的坐标;
(2)求出△BCO的面积;
(3)当PA+PC的值最小时,求此时点P的坐标.
【分析】(1)联立两直线解析式组成方程组,解得即可得出结论;
(2)把x=0代入y=x+3得B(0,3),结合C点坐标即可求面积;
(3)先确定出点A关于y轴的对称点A',即可求出PA+PC的最小值,再用待定系数法求出直线A'C的解析式即可得出点P坐标.
【解答】解:(1)∵直线l1:y=x+3①与直线l2:y=﹣3x②相交于C,
∴联立①②解得,x=﹣,y=,
∴C(﹣,);
(2)把x=0代入y=x+3得y=3,
∴B(0,3)
∴OB=3
∵C(﹣,)
∴△BCO的面积=OB×|﹣|═×3×=;
(3)在y=x+3中,当y=0时,x=﹣3
∴A(﹣3,0)
作点A(﹣3,0)关于y轴的对称点A′(3,0),连接CA′交y轴于点P,此时PC+PA最小,如图:
设直线CA′的解析式为y=kx+b
把C(﹣,),A′(3,0)代入上式得:
,
解得:
∴直线CA′的解析式为y=﹣x+
令x=0时y=
∴点P(0,).
【点评】此题是一次函数综合题,主要考查了函数图象的交点坐标的求法,待定系数法,用轴对称解决最短路径问题是解本题的关键.
2.已知,如图,在平面直角坐标系xoy中,直线l1:y=x+3分别交x轴、y轴于点A、B两点,直线l2:y=﹣3x过原点且与直线l1相交于C,点P为y轴上一动点.
(1)求点C的坐标;
(2)在平面坐标系中是否存在点M,使以A、O、C、M为顶点的四边形为平行四边形.若存在,求出点M的坐标;若不存在,请说明理由;
(3)当PA+PC的值最小时,求此时点P的坐标,并求PA+PC的最小值.
【分析】(1)联立两直线解析式组成方程组,解得即可得出结论;
(2)利用平行四边形的对角线互相平分和中点坐标公式即可得出结论;
(3)先确定出点A关于y轴的对称点A',即可求出PA+PC的最小值,再用待定系数法求出直线A'C的解析式即可得出点P坐标.
【解答】解:(1)∵直线l1:y=x+3①与直线l2:y=﹣3x②相交于C,
联立①②解得,x=﹣,y=,
∴C(﹣,);
(2)∵直线y=x+3交x轴于点A,
∴A(﹣3,0),
由(1)知,C(﹣,),
∵以A、O、C、M为顶点的四边形为平行四边形,
设M(m,n)如图1,
∴①当AC是对角线时,(﹣3﹣)=m,(0+)=n,
∴m=﹣,n=,
∴M(﹣,),
②当OC是对角线时,(0﹣)=(﹣3+m),(0+)=(0+n),
∴m=,n=,
M1(,),
③当OA为对角线时,(0﹣3)=(m﹣),(0+0)=(m+),
∴m=﹣,n=﹣.
M2(﹣,),
(3)如图2,作点A(﹣3,0)关于y轴的对称点A'(3,0),
连接CA'交y轴于点P,此时,PC+PA最小,最小值为CA'==,
由(1)知,C(﹣,),
∵A'(3,0),
∴直线A'C的解析式为y=﹣x+,
∴P(0,).
【点评】此题是一次函数综合题,主要考查了函数图象的交点坐标的求法,平行四边形的性质,待定系数法,极值的确定,用分类讨论的思想和方程(组)解决问题是解本题的关键.
3.问题情境:
平面直角坐标系中,矩形纸片OBCD按如图的方式放置.已知OB=10,BC=6,将这张纸片沿过点B的直线折叠,使点O落在边CD上,记作点A,折痕与边OD交于点E.
数学探究:
(1)点C的坐标为 (10,6) ;
(2)求点E的坐标及直线BE的函数关系式;
(3)若点P是x轴上的一点,直线BE上是否存在点Q,能使以A,B,P,Q为顶点的四边形是平行四边形?若存在,直接写出相应的点Q的坐标;若不存在,说明理由.
【分析】(1)利用矩形的性质的出货∠OBC=90°,即可得出结论;
(2)先利用勾股定理求出AC=8,进而利用勾股定理求出OE,得出点E坐标,最后用待定系数法即可得出结论;
(3)先求出点A坐标,再分两种情况,利用平行四边形的性质建立方程求解即可得出结论.
【解答】解:(1)∵四边形OBCD是矩形,
∴∠OBC=90°,
∵OB=10,BC=6,
∴C(10,6),
故答案为:(10,6);
(2)∵四边形OBCD是矩形,
∴OB=CD=10,AD=BC=6,∠C=∠ODC=90°,
设OE=m,
∴DE=OD﹣OE=6﹣m,
由折叠知,AB=OB=10,AE=OE=m,
在Rt△ABC中,根据勾股定理得,AC==8,
∴AD=CD﹣AC=10﹣8=2,
在Rt△ADE中,根据勾股定理得,AD2+DE2=AE2,
∴22+(6﹣m)2=m2,
∴m=,
∴E(0,),
设直线BE的函数关系式为y=kx+,
∵B(10,0),
∴10k+=0,
∴k=﹣,
∴直线BE的函数关系式为y=﹣x+;
(3)存在,理由:由(2)知,AD=2,
∴A(2,6),
∵能使以A,B,P,Q为顶点的四边形是平行四边形,
∴PQ∥AB,
①当BQ为的对角线时,
∴AQ∥BP,
∵点B,P在x轴,
∴Q的纵坐标等于点A的纵坐标6,
∵点Q在直线BE:y=﹣x+上,
∴﹣x+=6,
∴x=﹣8,
∴Q(﹣8,6),
②当BQ为边时,
∴AQ与BP互相平分,
设Q(n,﹣n+),
∴[6+(﹣n+)]=0,
∴n=28,
∴Q(28,﹣6),
即:直线BE上是存在点Q,能使以A,B,P,Q为顶点的四边形是平行四边形,点Q(﹣8,6)或(28,﹣6).
【点评】此题是一次函数综合题,主要考查了待定系数法,平行四边形的性质,矩形的性质,用方程的思想解决问题是解本题的关键.
4.如图,在平面直角坐标系中,直线分别与x轴、y轴交于点B、C,且与直线交于点A.
(1)分别求出点A、B、C的坐标;
(2)若D是线段OA上的点,且△COD的面积为12,求直线CD的函数表达式;
(3)在(2)的条件下,设P是射线CD上的点,在平面内是否存在点Q,使以O、C、P、Q为顶点的四边形是菱形?若存在,直接写出点Q的坐标;若不存在,请说明理由.
【分析】(1)把x=0,y=0分别代入直线L1,即可求出y和x的值,即得到B、C的坐标,解由直线BC和直线OA的方程组即可求出A的坐标;
(2)设D(x,x),代入面积公式即可求出x,即得到D的坐标,设直线CD的函数表达式是y=kx+b,把C(0,6),D(4,2)代入即可求出直线CD的函数表达式;
(3)存在点Q,使以O、C、P、Q为顶点的四边形是菱形,根据菱形的性质能写出Q的坐标.
【解答】解:(1)直线,
当x=0时,y=6,
当y=0时,x=12,
∴B(12,0),C(0,6),
解方程组:得:,
∴A(6,3),
答:A(6,3),B(12,0),C(0,6).
(2)解:设D(x,x),
∵△COD的面积为12,
∴×6×x=12,
解得:x=4,
∴D(4,2),
设直线CD的函数表达式是y=kx+b,把C(0,6),D(4,2)代入得:
,
解得:,
∴y=﹣x+6,
答:直线CD的函数表达式是y=﹣x+6.
(3)答:存在点Q,如图,
使以O、C、P、Q为顶点的四边形是菱形,点Q的坐标是(6,6)或(﹣3,3)或.
【点评】本题主要考查了一次函数图象上点的坐标特征,用待定系数法求一次函数的解析式,解二元一次方程组,菱形的性质,三角形的面积等知识点,解此题的关键是熟练地运用知识进行计算.此题是一个综合性很强的题目.
5.如图,在直角坐标系中,OA=3,OC=4,点B是y轴上一动点,以AC为对角线作平行四边形ABCD.
(1)求直线AC的函数解析式;
(2)设点B(0,m),记平行四边形ABCD的面积为S,请写出S与m的函数关系式,并求当BD取得最小值时的S的值;
(3)当点B在y轴上运动,在使得平行四边形ABCD是菱形的同时,在x轴取一点P,使得△PAB是等腰三角形,请直接写出点P的坐标.
【分析】(1)根据OA、OC的长度结合图形可得出点A、C的坐标,再利用待定系数法即可求出直线AC的解析式;
(2)根据点B的坐标可得出BC的长度,结合平行四边形的面积公式即可得出S关于m的函数关系式,再根据AD∥y轴即可找出当BD最短时m的值,将其代入S关于m的函数关系式中即可得出结论;
(3)根据菱形的性质找出m的值,从而找出点B的坐标,设点P的坐标为(n,0),根据两点间的距离公式找出AP、BP、AB的长度,分AP=BP、AP=AB、BP=AB三种情况求出n值,再将其代入点P的坐标中即可得出结论.
【解答】解:(1)∵OA=3,OC=4,
∴A(﹣3,0)、C(0,4).
设直线AC的函数解析式为y=kx+b,
将点A(﹣3,0)、C(0,4)代入y=kx+b中,
得:,解得:,
∴直线AC的函数解析式为y=x+4.
(2)∵点B(0,m),四边形ABCD为以AC为对角线的平行四边形,
∴BC=|4﹣m|,
∴S=BC?OA=|﹣3m+12|(m≠4).
∵四边形ABCD为平行四边形,
∴AD∥BC,
∴当BD⊥y轴时,BD最小(如图1).
∵AD∥OB,AO⊥OB,DA⊥OB,
∴四边形AOBD为矩形,
∴AD=OB=BC,
∴点B为OC的中点,即m==2,
此时S=|﹣3×2+12|=6.
∴S与m的函数关系式为S=|﹣3m+12|(m≠4),当BD取得最小值时的S的值为6.
(3)∵平行四边形ABCD是菱形,
∴AB=BC.
∵AB==,BC=4﹣m,
∴=4﹣m,
解得:m=,
∴B(0,).
设点P的坐标为(n,0),
∵A(﹣3,0),B(0,),
∴PA=|n+3|,PB=,AB=4﹣=.
△PAB是等腰三角形分三种情况:
①当PA=PB时,有|n+3|=,
解得:n=﹣,
此时点P的坐标为(﹣,0);
②当PA=AB时,有|n+3|=,
解得:n1=,n2=﹣,
此时点P的坐标为(﹣,0)或(,0);
③当PB=AB时,有=,
解得:n3=﹣3(舍去),n4=3,
此时点P的坐标为(3,0).
综上可知:点P的坐标为(﹣,0)、(﹣,0)、(,0)或(3,0).
【点评】本题考查了待定系数法求函数解析式、平行四边形的性质、菱形的性质以及等腰三角形的性质,解题的关键是:(1)利用待定系数法求出函数解析式;(2)根据平行四边形的面积公式找出S关于m的函数关系式;(3)分三种情况讨论.本题属于中档题,难度不大,解决该题型题目时,熟练掌握多边形的性质是关键.
6.已知:如图,已知直线AB的函数解析式为y=﹣2x+8,与x轴交于点A,与y轴交于点B.
(1)求A、B两点的坐标;
(2)若点P(m,n)为线段AB上的一个动点(与A、B不重合),作PE⊥x轴于点E,PF⊥y轴于点F,连接EF,问:
①若△PAO的面积为S,求S关于m的函数关系式,并写出m的取值范围;
②是否存在点P,使EF的值最小?若存在,求出EF的最小值;若不存在,请说明理由.
【分析】(1)利用待定系数法即可解决问题;
(2)①连接OP,根据三角形的面积公式S△PAO=×OA×PE计算即可;
②存在,首先证明四边形OEPF是矩形,可得EF=OP,根据垂线段最短可知:当OP⊥AB时,此时EF最小;
【解答】解:(1)令x=0,则y=8,
∴B(0,8),
令y=0,则﹣2x+8=0,
∴x=4,
∴A(4,0),
(2)①连接OP.
∵点P(m,n)为线段AB上的一个动点,
∴﹣2m+8=n,∵A(4,0),
∴OA=4,
∴0<m<4
∴S△PAO=×OA×PE=×4×n=2(﹣2m+8)=﹣4m+16,(0<m<4);
②存在,
理由:∵PE⊥x轴于点E,PF⊥y轴于点F,OA⊥OB,
∴四边形OEPF是矩形,
∴EF=OP,
当OP⊥AB时,此时EF最小,
∵A(4,0),B(0,8),
∴AB=4
∵S△AOB=×OA×OB=×AB×OP,
∴OP===,
∴EF的最小值=OP=.
【点评】本题考查一次函数的性质、矩形的性质、三角形的面积等知识,解题的关键是学会用转化的思想思考问题,属于中考常考题型.
7.如图,在平面直角坐标系中,直线y=2x+4与坐标轴分别交于A、B两点,点C在x轴上,且OA=OC,点P从A出发沿射线AC方向运动,速度为每秒1个单位长度,设运动时间为t(s).
(1)求点B、C的坐标;
(2)若△OCP的面积为4,求运动时间t的值;
(3)如图2,若∠POQ=90°,且OP=OQ,连接BQ,求运动过程中BQ的最小值.
【分析】(1)在y=2x+4中分别令x=0和y=0,则可求得A、B坐标,结合OA=OC可求得C点坐标;
(2)由条件可求得点O到直线AC的距离,用t可表示出PC的长,则可表示出△OCP的面积,可得到关于t的方程,可求得t的值;
(3)连接AQ,可证明△OQA≌△OPC,则可知∠OAQ=45°,可求得直线AQ的解析式,设直线AQ交x轴于点E,则当BQ⊥AE时,BQ最短,可求得BQ的长.
【解答】解:
(1)在y=2x+4中,令x=0可得y=4,令y=0可得2x+4=0,解得x=﹣2,
∴A(0,4),B(,0),
∴OC=OA=4,
∴C(,0);
(2)∵OA=OC=4,
∴AC=8,
∴点O到直线AC的距离为4,
当运动t秒时,则AP=t,则CP=|AP﹣AC|=|t﹣8|,
∴S△OCP=×4|t﹣8|=2|t﹣8|,
∵△OCP的面积为4,
∴2|t﹣8|=4,解得t=6或t=10,
即当t为6秒或10秒时,△OCP的面积为4;
(3)如图,连接AQ,
∵∠POQ=90°,∠AOC=90°,
∴∠QOA+∠AOP=∠AOP+∠POC,
∴∠AOQ=∠COP,
在△OQA和△OPC中
∴△OQA≌△OPC(SAS),
∴∠OCP=∠OAQ=45°,
设直线AQ交x轴于点E,则E(﹣4,0),
∴BE=2,
设直线AQ解析式为y=kx+b,
∴,解得,
∴直线AQ解析式为y=x+4,
∴点Q始终在直线上,
∴BQ⊥AE时,BQ最短,
此时BQ=2,即BQ的最小值为2.
【点评】本题为一次函数的综合应用,涉及函数与坐标轴的交点、三角形的面积、全等三角形的判定和性质、待定系数法、最短距离及方程思想等知识.在(2)中用t表示出△OCP的面积是解题的关键,在(3)中确定出点Q的位置是解题的关键.本题考查知识点较多,综合性较强,难度适中.
8.如图,矩形OABC放在以O为原点的平面直角坐标系中,A(3,0),C(0,2),点E是AB的中点,点F在BC边上,且CF=1.
(1)点E的坐标为 (3,1) ,点F的坐标为 (1,2) ;
(2)点E关于x轴的对称点为E′,点F关于y轴的对称点为F′,
①点E′的坐标为 (3,﹣1) ,点F′的坐标为 (﹣1,2) ;
②求直线E′F′的解析式;
(3)若M为x轴上的动点,N为y轴上的动点,当四边形MNFE的周长最小时,求出点M,N的坐标,并求出周长的最小值.
【分析】(1)先求出OA,OC,再根据矩形的性质得出BA=2,即可得出结论;
(2)①利用对称的性质即可得出结论;
②利用待定系数法即可求出直线E'F'解析式;
(3)先判断出点M,N是直线E'F'和x,y轴的交点,再利用两点间的距离公式即可得出结论.
【解答】解:(1)∵A(3,0),B(0,2),
∴OA=3,OC=2,
∵四边形OABC是矩形,
∴BC∥OA,OC∥AB,BC=OA=3,AB=OC=2,
∴C(3,2),
∵点E是AB的中点,
∴AE=AB=1,
∴E(3,1),
∵点F在BC上,且CF=1,
∴F(1,2),
故答案为:(3,1),(1,2),
(2)①由(1)知,E(3,1),F(1,2),
∵点E关于x轴的对称点为E′,点F关于y轴的对称点为F′,
∴E'(3,﹣1),F'(﹣1,2),
故答案为:(3,﹣1),F'(﹣1,2);
②设直线E'F'的解析式为y=kx+b,
∴,
∴,
∴直线E'F'的解析式为y=﹣x+;
(3)如图,∵E(3,1),F(1,2),
∴EF=,
∵点E关于x轴的对称点为E′,点F关于y轴的对称点为F′,
∴连接E'F'和x轴交于M,和y轴交于N,此时四边形MNFE的周长最小,
∴NF=NF',ME=ME',
∵E'(3,﹣1),F'(﹣1,2),
∴E'F==5,
∴四边形MNFE的周长的最小值为NF+MN+ME+EF
=NF'+MN+ME'+EF=E'F'+EF=5+.
【点评】此题是四边形综合题,主要考查了矩形的性质,对称的性质,待定系数法,两点间的距离公式,解(2)的关键是求出点E',F'的坐标,解(3)的关键是判断出点M,N的位置,是一道常规题.
9.如图,在平面直角坐标系中,过点B(6,0)的直线AB与直线OA相交于点A(4,2),动点M沿路线O→A→C运动.
(1)求直线AB的解析式.
(2)求△OAC的面积.
(3)当△OMC的面积是△OAC的面积的时,求出这时点M的坐标.
【分析】(1)利用待定系数法即可求得函数的解析式;
(2)求得C的坐标,即OC的长,利用三角形的面积公式即可求解;
(3)当△OMC的面积是△OAC的面积的时,根据面积公式即可求得M的横坐标,然后代入解析式即可求得M的坐标.
【解答】解:(1)设直线AB的解析式是y=kx+b,
根据题意得:,
解得:,
则直线的解析式是:y=﹣x+6;
(2)在y=﹣x+6中,令x=0,解得:y=6,
S△OAC=×6×4=12;
(3)设OA的解析式是y=mx,则4m=2,
解得:m=,
则直线的解析式是:y=x,
∵当△OMC的面积是△OAC的面积的时,
∴M的横坐标是×4=1,
在y=x中,当x=1时,y=,则M的坐标是(1,);
在y=﹣x+6中,x=1则y=5,则M的坐标是(1,5).
则M的坐标是:M1(1,)或M2(1,5).
【点评】本题主要考查了用待定系数法求函数的解析式.先根据条件列出关于字母系数的方程,解方程求解即可得到函数解析式.当已知函数解析式时,求函数中字母的值就是求关于字母系数的方程的解.
10.如图1,已知直线y=2x+2与y轴、x轴分别交于A、B两点,以B为直角顶点在第二象限作等腰Rt△ABC.
(1)求点C的坐标,并求出直线AC的关系式.
(2)如图2,直线CB交y轴于E,在直线CB上取一点D,连接AD,若AD=AC,求证:BE=DE.
(3)如图3,在(1)的条件下,直线AC交x轴于M,P(,k)是线段BC上一点,在线段BM上是否存在一点N,使直线PN平分△BCM的面积?若存在,请求出点N的坐标;若不存在,请说明理由.
【分析】(1)如图1,作CQ⊥x轴,垂足为Q,利用等腰直角三角形的性质证明△ABO≌△BCQ,根据全等三角形的性质求OQ,CQ的长,确定C点坐标;
(2)同(1)的方法证明△BCH≌△BDF,再根据线段的相等关系证明△BOE≌△DGE,得出结论;
(3)依题意确定P点坐标,可知△BPN中BN边上的高,再由S△PBN=S△BCM,求BN,进而得出ON.
【解答】解:(1)如图1,作CQ⊥x轴,垂足为Q,
∵∠OBA+∠OAB=90°,∠OBA+∠QBC=90°,
∴∠OAB=∠QBC,
又∵AB=BC,∠AOB=∠CQB=90°,
∴△ABO≌△BCQ,
∴BQ=AO=2,OQ=BQ+BO=3,CQ=OB=1,
∴C(﹣3,1),
由A(0,2),C(﹣3,1)可知,直线AC:y=x+2;
(2)如图2,作CH⊥x轴于H,DF⊥x轴于F,DG⊥y轴于G,
∵AC=AD,AB⊥CB,
∴BC=BD,
∴△BCH≌△BDF,
∴BF=BH=2,
∴OF=OB=1,
∴DG=OB,
∴△BOE≌△DGE,
∴BE=DE;
(3)如图3,直线BC:y=﹣x﹣,P(,k)是线段BC上一点,
∴P(﹣,),
由y=x+2知M(﹣6,0),
∴BM=5,则S△BCM=.
假设存在点N使直线PN平分△BCM的面积,
则BN?=×,
∴BN=,ON=,
∵BN<BM,
∴点N在线段BM上,
∴N(﹣,0).
【点评】本题考查了一次函数的综合运用.关键是根据等腰直角三角形的特殊性证明全等三角形,利用全等三角形的性质求解.
11.【背景知识】研究平面直角坐标系,我们可以发现一条重要的规律:若平面直角坐标系上有两个不同的点A(xA,yA)、B(xB,yB),则线段AB的中点坐标可以表示为(,).
【简单应用】如图1,直线AB与y轴交于点A(0,3),与x轴交于点B(4,0),过原点O的直线L将△ABO分成面积相等的两部分,请求出直线L的解析式;
【探究升级】小明发现“若四边形一条对角线平分四边形的面积,则这条对角线必经过另一条对角线的中点”
如图2,在四边形ABCD中,对角线AC、BD相交于点O,S△ABD=S△BCD.试说明AO=CO;
【综合运用】如图3,在平面直角坐标系中A(1,4),B(3,﹣2),C(2m,﹣m+5),若OC恰好平分四边形OACB的面积,求点C的坐标.
【分析】【简单应用】先判断出直线L过线段AB的中点,再求出线段AB的中点,最后用待定系数法即可得出结论;
【探究升级】先判断出AF=CG,进而判断出△AOF≌△COG,即可得出结论;
【综合运用】借助【探究升级】的结论判断出直线OC过线段AB的中点,进而求出直线OC的解析式,最后将点C坐标代入即可得出结论.
【解答】解:【简单应用】:∵直线L将△ABO分成面积相等的两部分,
∴直线L必过相等AB的中点,
设线段AB的中点为E,
∵A(0,3),B(4,0),
∴E(,),
∴E(2,),
∵直线L过原点,
∴设直线L的解析式为y=kx,
∴2k=,
∴k=,
∴直线L的解析式为y=x;
【探究升级】:如图2,
过点A作AF⊥BD于F,过点C作CG⊥BD于G,
∴S△ABD=BD?AF,S△CBD=BD?CG,
∵S△ABD=S△BCD,
∴BD?AF=BD?CG,
∴AF=CG,
在△AOF和△COG中,,
∴△AOF≌△COG(AAS),
∴OA=OC;
【综合运用】:如图3,
由【探究升级】知,若四边形一条对角线平分四边形的面积,则这条对角线必经过另一条对角线的中点,
∵OC恰好平分四边形OACB的面积,
∴OC过四边形OACB的对角线OA的中点,
连接AB,设线段AB的中点为H,
∵A(1,4),B(3,﹣2),
∴H(2,1),设直线OC的解析式为y=k'x,
∴2k'=1,
∴k'=,
∴直线OC的解析式为y=x,
∵点C(2m,﹣m+5)在直线OC上,
∴﹣m+5=×2m,
∴m=,
∴C(5,).
【点评】此题是一次函数综合题,主要考查了待定系数法,三角形的中线的性质,全等三角形的判定和性质,构造出全等三角形是解本题的关键.
12.如图,四边形ABCD是正方形,E是边AB上一点,连接DE,将直线DE绕点D逆时针旋转90°,交BC的延长线于点F
(1)如图1,求证:DE=DF;
(2)如图2,连接EF,若D关于直线EF的对称点为H,连接CH,过点H作PH⊥CH交AB于点P,求证:E是AP的中点;
(3)如图3,在(2)的条件下,连接AC交EF于点G,连接BG、BH,若BG=2,AB=6,求线段PH的长.
【分析】(1)由正方形的性质可得AB=AD=CD,∠A=∠ADC=90°=∠BCD,由“SAS”可证△ADE≌△CDF,可得DE=DF;
(2)如图2,连接EH,FH,由轴对称性质可得EH=DE=FH=DF,由余角的性质和三角形内角和定理可得∠EPH=∠HCF,∠EHP=∠CHF,由“ASA”可证△EHP≌△FHC,可得PE=CF,即可得结论;
(3)如图3,连接PC,EH,FH,过点E作EK∥BC,交AC于K,由正方形的性质和平行线的性质可得∠AKE=∠ACB=45°=∠EAK,∠AEK=∠ABC=90°,∠EKG=∠GCF,由“AAS”可证△EKG≌△FCG,可得EG=FG,由直角三角形的性质可得EG=GF=BG=2,由勾股定理可求BP的长,PC的长,由等腰直角三角形的性质可求PH的长.
【解答】证明:(1)∵四边形ABCD是正方形,
∴AB=AD=CD,∠A=∠ADC=90°=∠BCD,
∵将直线DE绕点D逆时针旋转90°,
∴∠EDF=90°,
∴∠ADC=∠EDF,
∴∠ADE=∠CDF,且AD=CD,∠A=∠DCF=90°,
∴△ADE≌△CDF(SAS),
∴DE=DF,
(2)如图2,连接EH,FH,
∵点D关于直线EF的对称点为H,
∴EH=DE,FH=DF,且DE=DF,
∴EH=DE=FH=DF,
∵DE=EH,DF=HF,EF=EF,
∴△DEF≌△HEF(SSS)
∴∠EHF=∠EDF=90°,且PH⊥CH,
∴∠PHE=∠FHC,
∵∠B=∠PHC=90°,∠BGP=∠CGH,
∴∠BPG=∠HCG,
∴∠EPH=∠HCF,且EH=HF,∠EHP=∠CHF,
∴△EHP≌△FHC(AAS)
∴EP=CF,
∵△ADE≌△CDF,
∴AE=CF,
∴AE=EP,
∴点E是AP中点,
(3)如图3,连接PC,EH,FH,过点E作EK∥BC,交AC于K,
∵EK∥BC,
∴∠AKE=∠ACB=45°=∠EAK,∠AEK=∠ABC=90°,∠EKG=∠GCF,
∴AE=EK,
∵AE=CF,
∴EK=CF,且∠EKG=∠GCF,∠EGK=∠CGF,
∴△EKG≌△FCG(AAS)
∴EG=FG,
∵BG=2,
∴EG=FG=BG=2,
∴EF=4,
∵EF2=BE2+BF2,
∴80=(6﹣AE)2+(6+AE)2,
∴AE=2
∴BP=AB﹣AE﹣EP=2
∴PC===2
由(2)可知△EHP≌△FHC,
∴PH=CH,且PH⊥CH
∴PC=PH
∴PH=2
【点评】本题是四边形综合题,考查了正方形的性质,全等三角形的判定和性质,直角三角形的性质,勾股定理等知识,添加恰当辅助线构造全等三角形是本题的关键.
13.如图,四边形ABCD是正方形,E是边AB上一点,连接DE,直线DE绕着点D逆时针旋转90°,交BC的延长线于点F.
(1)如图1,求证:DE=DF;
(2)如图2,连接EF,若D关于直线EF的对称点为H,连接CH,过点H作PH⊥CH交AB于点P,求证:E为AP中点;
(3)如图3,在(2)的条件下,连接AC交EF于点G,连接BG,BH,若BG=,AB=3,求线段PH的长.
【分析】(1)全等三角形是证明两条线段相等的重要方法之一.只要证明△ADE≌△CDF,即可得到DE=DF;
(2)连接HE,HF,由点H与点D关于直线EF对称,所以EH=ED,FH=FD.因为DE=DF,所以EH=FH=ED=FD.即四边形DEHF是菱形.由∠EDF=90°,得到四边形DEHF是正方形,利用正方形的性质证明△HPE≌△HCF,得到PE=CF,所以AE=PE,得到点E是AP的中点;
(3)过点E作EK∥BF,只要证明△EGK≌△CFG,可得EG=GF,推出EF=2BG=2,设AE=CF=a
则BE=3﹣a,BF=3+a,可得(3﹣a)2+(3+a)2=(2
)2,再证明△PCH是等腰直角三角形,求出PC即可解决问题;
【解答】证明:(1)∵直线DE绕着点D逆时针旋转90°,
∴∠EDF=90°,
∵四边形ABCD是正方形,
∴∠ADC=∠A=∠DCB=90°,AD=DC
∴∠ADC=∠EDF=∠DCF=∠A=90°,
∴∠ADC﹣∠EDC=∠EDF﹣∠EDC,
即∠ADE=∠CDF,
在△ADE与△CDF中,
,
∴△ADE≌△CDF(ASA),
∴DE=DF;
(2)连接EH,FH,如图2
∵D、H关于EF对称,
∴EF垂直平分DH,
∴HE=DE,DF=HF,
又∵EF=EF,
∴△EDF≌△EHF,
∴∠EHF=∠EDF=90°,
又∵∠B=∠EHF=90°,
∴∠BPH=∠BCH,
∴∠EPH=∠FCH,
又∵DE=DF,
∴EH=HF,
又∵PH⊥CH,
∴∠PHC=∠EHF=90°,
∴∠PHE=∠CHF,
∴△PEH≌△CFH,
∴CF=PE,
又∵△ADE≌△CDF
∴AE=CF,
∴AE=PE,
∴E为AP中点;
(3)过点E作EK∥BF,如图3:
∵EK∥BF,
∴∠EKA=∠BCA=45°,∠EKG=∠FCG,
∴∠EAK=∠EKA=45°,
∴EA=EK=CF,
又∵∠EGK=∠CGF,
∴△EGK≌△CFG,
∴EG=GF,
∴在Rt△EBF中,EF=2BG=2
,
∴设AE=CF=a
则BE=3﹣a,BF=3+a,
∴(3﹣a)2+(3+a)2=(2
)2
∴a=1(a=﹣1舍),
∴AE=PE=1,
∴BP=1,
连接PC,
∴PC==,
由(2)可知△PEH≌△CFH,
∴HP=HC,∠PHE=∠CHF,
∴∠PHC=∠EHF=90°,
∴△PCH是等腰直角三角形,
∴PH=HC=×=.
【点评】本题考查了正方形的性质,全等三角形的判定定理和性质定理,勾股定理的应用,对称的性质,等腰直角三角形的性质等知识,解决本题的关键是利用正方形的性质得到相等的边和相等的角,证明三角形全等,作出辅助线也是解决本题的关键.
14.如图1,在△ABC中,∠ACB为锐角,点D为射线BC上一点,联结AD,以AD为一边且在AD的右侧作正方形ADEF.
(1)如果AB=AC,∠BAC=90°,
①当点D在线段BC上时(与点B不重合),如图2,将△ABD绕A点逆时针旋转90°,所得到的三角形为 △ACF ,线段CF、BD所在直线的位置关系为 互相垂直 ,线段CF、BD的数量关系为 相等 ;
②当点D在线段BC的延长线上时,如图3,①中的结论是否仍然成立,并说明理由;
(2)如果AB≠AC,∠BAC是锐角,点D在线段BC上,当∠ACB满足什么条件时,CF⊥BC(点C、F不重合),并说明理由.
【分析】(1)①当点D在线段BC上时,根据等腰直角三角形的性质以及旋转的性质,即可得出CF=BD,BD⊥CF;②当点D在BC的延长线上时,①的结论仍成立.由正方形ADEF的性质可推出△DAB≌△FAC,所以CF=BD,∠ACF=∠ABD,结合∠BAC=90°,AB=AC,得到∠BCF=∠ACB+∠ACF=90°,即CF⊥BD;
(2)当∠ACB=45°时,过点A作AG⊥AC交CB的延长线于点G,则∠GAC=90°,可推出∠ACB=∠AGC,所以AC=AG,由(1)①中的方法可得CF⊥BD.
【解答】解:(1)①如图2所示,将△ABD绕A点逆时针旋转90°,所得到△ACF,则
由旋转的性质可得:∠ACF=∠B,CF=BD,
∵AB=AC,∠BAC=90°,
∴∠B=∠ACB=45°=∠ACF,
∴∠BCF=90°,即BD⊥CF;
故答案为:△ACF,垂直,相等;
②如图3所示,当点D在BC的延长线上时,①中的结论仍成立.
证明:由正方形ADEF得,AD=AF,∠DAF=90°.
∵∠BAC=90°
∴∠DAF=∠BAC,
∴∠DAB=∠FAC,
又∵AB=AC,
∴△DAB≌△FAC(SAS),
∴CF=BD,∠ACF=∠ABD.
∵∠BAC=90°,AB=AC,
∴∠ABC=45°,
∴∠ACF=45°,
∴∠BCF=∠ACB+∠ACF=90°,即
CF⊥BD;
(2)如图4所示,当∠ACB=45°时,CF⊥BD.
理由:过点A作AG⊥AC交CB或CB的延长线于点G,则∠GAC=90°,
∵∠ACB=45°,∠AGC=90°﹣∠ACB=45°,
∴∠ACB=∠AGC,
∴AC=AG,
又∵∠DAG=∠FAC(同角的余角相等),AD=AF,
∴△GAD≌△CAF(SAS),
∴∠ACF=∠AGC=45°,
∴∠BCF=∠ACB+∠ACF=45°+45°=90°,即CF⊥BC.
【点评】本题主要考查正方形的性质,余角的性质,三角形全等的判定和直角三角形的判定,判定两个三角形全等,先根据已知条件或求证的结论确定三角形,然后再根据三角形全等的判定方法,看缺什么条件,再去证什么条件.解题的关键是过点A作AG⊥AC交CB的延长线于点G,构造全等三角形.
15.如图,正方形ABCD中,AC是对角线,今有较大的直角三角板,一边始终经过点B,直角顶点P在射线AC上移动,另一边交DC于Q.
(1)如图1,当点Q在DC边上时,猜想并写出PB与PQ所满足的数量关系;并加以证明;
(2)如图2,当点Q落在DC的延长线上时,猜想并写出PB与PQ满足的数量关系,请证明你的猜想.
【分析】(1)过P作PE⊥BC,PF⊥CD,证明Rt△PQF≌Rt△PBE,即可;
(2)证明思路同(1)
【解答】(1)PB=PQ,
证明:过P作PE⊥BC,PF⊥CD,
∵P,C为正方形对角线AC上的点,
∴PC平分∠DCB,∠DCB=90°,
∴PF=PE,
∴四边形PECF为正方形,
∵∠BPE+∠QPE=90°,∠QPE+∠QPF=90°,
∴∠BPE=∠QPF,
∴Rt△PQF≌Rt△PBE,
∴PB=PQ;
(2)PB=PQ,
证明:过P作PE⊥BC,PF⊥CD,
∵P,C为正方形对角线AC上的点,
∴PC平分∠DCB,∠DCB=90°,
∴PF=PE,
∴四边形PECF为正方形,
∵∠BPF+∠QPF=90°,∠BPF+∠BPE=90°,
∴∠BPE=∠QPF,
∴Rt△PQF≌Rt△PBE,
∴PB=PQ.
【点评】此题考查了正方形,角平分线的性质,以及全等三角形判定与性质.此题综合性较强,注意数形结合思想.
八年级下册4-5章专题培优
一次函数中的特殊四边形
1.已知,如图,在平面直角坐标系xOy中,直线l1:y=x+3分别交x轴、y轴于点A、B两点,直线l2:y=﹣3x过原点且与直线l1相交于C,点P为y轴上一动点.
(1)求点C的坐标;
(2)求出△BCO的面积;
(3)当PA+PC的值最小时,求此时点P的坐标.
2.已知,如图,在平面直角坐标系xoy中,直线l1:y=x+3分别交x轴、y轴于点A、B两点,直线l2:y=﹣3x过原点且与直线l1相交于C,点P为y轴上一动点.
(1)求点C的坐标;
(2)在平面坐标系中是否存在点M,使以A、O、C、M为顶点的四边形为平行四边形.若存在,求出点M的坐标;若不存在,请说明理由;
(3)当PA+PC的值最小时,求此时点P的坐标,并求PA+PC的最小值.
3.问题情境:
平面直角坐标系中,矩形纸片OBCD按如图的方式放置.已知OB=10,BC=6,将这张纸片沿过点B的直线折叠,使点O落在边CD上,记作点A,折痕与边OD交于点E.
数学探究:
(1)点C的坐标为
;
(2)求点E的坐标及直线BE的函数关系式;
(3)若点P是x轴上的一点,直线BE上是否存在点Q,能使以A,B,P,Q为顶点的四边形是平行四边形?若存在,直接写出相应的点Q的坐标;若不存在,说明理由.
4.如图,在平面直角坐标系中,直线分别与x轴、y轴交于点B、C,且与直线交于A.
(1)分别求出点A、B、C的坐标;
(2)若D是线段OA上的点,且△COD的面积为12,求直线CD的函数表达式;
(3)在(2)的条件下,设P是射线CD上的点,在平面内是否存在点Q,使以O、C、P、Q为顶点的四边形是菱形?若存在,直接写出点Q的坐标;若不存在,请说明理由.
5.如图,在直角坐标系中,OA=3,OC=4,点B是y轴上一动点,以AC为对角线作平行四边形ABCD.
(1)求直线AC的函数解析式;
(2)设点B(0,m),记平行四边形ABCD的面积为S,请写出S与m的函数关系式,并求当BD取得最小值时的S的值;
(3)当点B在y轴上运动,在使得平行四边形ABCD是菱形的同时,在x轴取一点P,使得△PAB是等腰三角形,请直接写出点P的坐标.
6.已知:如图,已知直线AB的函数解析式为y=﹣2x+8,与x轴交于点A,与y轴交于点B.
(1)求A、B两点的坐标;
(2)若点P(m,n)为线段AB上的一个动点(与A、B不重合),作PE⊥x轴于点E,PF⊥y轴于点F,连接EF,问:
①若△PAO的面积为S,求S关于m的函数关系式,并写出m的取值范围;
②是否存在点P,使EF的值最小?若存在,求出EF的最小值;若不存在,请说明理由.
7.如图,在平面直角坐标系中,直线y=2x+4与坐标轴分别交于A、B两点,点C在x轴上,且OA=OC,点P从A出发沿射线AC方向运动,速度为每秒1个单位长度,设运动时间为t(s).
(1)求点B、C的坐标;
(2)若△OCP的面积为4,求运动时间t的值;
(3)如图2,若∠POQ=90°,且OP=OQ,连接BQ,求运动过程中BQ的最小值.
8.如图,矩形OABC放在以O为原点的平面直角坐标系中,A(3,0),C(0,2),点E是AB的中点,点F在BC边上,且CF=1.
(1)点E的坐标为
,点F的坐标为
;
(2)点E关于x轴的对称点为E′,点F关于y轴的对称点为F′,
①点E′的坐标为
,点F′的坐标为
;
②求直线E′F′的解析式;
(3)若M为x轴上的动点,N为y轴上的动点,当四边形MNFE的周长最小时,求出点M,N的坐标,并求出周长的最小值.
9.如图,在平面直角坐标系中,过点B(6,0)的直线AB与直线OA相交于点A(4,2),动点M沿路线O→A→C运动.
(1)求直线AB的解析式.
(2)求△OAC的面积.
(3)当△OMC的面积是△OAC的面积的时,求出这时点M的坐标.
10.如图1,已知直线y=2x+2与y轴、x轴分别交于A、B两点,以B为直角顶点在第二象限作等腰Rt△ABC.
(1)求点C的坐标,并求出直线AC的关系式.
(2)如图2,直线CB交y轴于E,在直线CB上取一点D,连接AD,若AD=AC,求证:BE=DE.
(3)如图3,在(1)的条件下,直线AC交x轴于M,P(—,k)是线段BC上一点,在线段BM上是否存在一点N,使直线PN平分△BCM的面积?若存在,请求出点N的坐标;若不存在,请说明理由.
11.【背景知识】研究平面直角坐标系,我们可以发现一条重要的规律:若平面直角坐标系上有两个不同的点A(xA,yA)、B(xB,yB),则线段AB的中点坐标可以表示为(,).
【简单应用】如图1,直线AB与y轴交于点A(0,3),与x轴交于点B(4,0),过原点O的直线L将△ABO分成面积相等的两部分,请求出直线L的解析式;
【探究升级】小明发现“若四边形一条对角线平分四边形的面积,则这条对角线必经过另一条对角线的中点”
如图2,在四边形ABCD中,对角线AC、BD相交于点O,S△ABD=S△BCD.试说明AO=CO;
【综合运用】如图3,在平面直角坐标系中A(1,4),B(3,﹣2),C(2m,﹣m+5),若OC恰好平分四边形OACB的面积,求点C的坐标.
12.如图,四边形ABCD是正方形,E是边AB上一点,连接DE,将直线DE绕点D逆时针旋转90°,交BC的延长线于点F
(1)如图1,求证:DE=DF;
(2)如图2,连接EF,若D关于直线EF的对称点为H,连接CH,过点H作PH⊥CH交AB于点P,求证:E是AP的中点;
(3)如图3,在(2)的条件下,连接AC交EF于点G,连接BG、BH,若BG=2,AB=6,求线段PH的长.
13.如图,四边形ABCD是正方形,E是边AB上一点,连接DE,直线DE绕着点D逆时针旋转90°,交BC的延长线于点F.
(1)如图1,求证:DE=DF;
(2)如图2,连接EF,若D关于直线EF的对称点为H,连接CH,过点H作PH⊥CH交AB于点P,求证:E为AP中点;
(3)如图3,在(2)的条件下,连接AC交EF于点G,连接BG,BH,若BG=,AB=3,求线段PH的长.
14.如图1,在△ABC中,∠ACB为锐角,点D为射线BC上一点,联结AD,以AD为一边且在AD的右侧作正方形ADEF.
(1)如果AB=AC,∠BAC=90°,
①当点D在线段BC上时(与点B不重合),如图2,将△ABD绕A点逆时针旋转90°,所得到的三角形为
,线段CF、BD所在直线的位置关系为
,线段CF、BD的数量关系为
;
②当点D在线段BC的延长线上时,如图3,①中的结论是否仍然成立,并说明理由;
(2)如果AB≠AC,∠BAC是锐角,点D在线段BC上,当∠ACB满足什么条件时,CF⊥BC(点C、F不重合),并说明理由.
15.如图,正方形ABCD中,AC是对角线,今有较大的直角三角板,一边始终经过点B,直角顶点P在射线AC上移动,另一边交DC于Q.
(1)如图1,当点Q在DC边上时,猜想并写出PB与PQ所满足的数量关系;并加以证明;
(2)如图2,当点Q落在DC的延长线上时,猜想并写出PB与PQ满足的数量关系,请证明你的猜想.
浙教版数学
八年级下册4-5章专题培优
一次函数中的特殊四边形
参考答案与试题解析
一.解答题(共15小题)
1.已知,如图,在平面直角坐标系xOy中,直线l1:y=x+3分别交x轴、y轴于点A、B两点,直线l2:y=﹣3x过原点且与直线l1相交于C,点P为y轴上一动点.
(1)求点C的坐标;
(2)求出△BCO的面积;
(3)当PA+PC的值最小时,求此时点P的坐标.
【分析】(1)联立两直线解析式组成方程组,解得即可得出结论;
(2)把x=0代入y=x+3得B(0,3),结合C点坐标即可求面积;
(3)先确定出点A关于y轴的对称点A',即可求出PA+PC的最小值,再用待定系数法求出直线A'C的解析式即可得出点P坐标.
【解答】解:(1)∵直线l1:y=x+3①与直线l2:y=﹣3x②相交于C,
∴联立①②解得,x=﹣,y=,
∴C(﹣,);
(2)把x=0代入y=x+3得y=3,
∴B(0,3)
∴OB=3
∵C(﹣,)
∴△BCO的面积=OB×|﹣|═×3×=;
(3)在y=x+3中,当y=0时,x=﹣3
∴A(﹣3,0)
作点A(﹣3,0)关于y轴的对称点A′(3,0),连接CA′交y轴于点P,此时PC+PA最小,如图:
设直线CA′的解析式为y=kx+b
把C(﹣,),A′(3,0)代入上式得:
,
解得:
∴直线CA′的解析式为y=﹣x+
令x=0时y=
∴点P(0,).
【点评】此题是一次函数综合题,主要考查了函数图象的交点坐标的求法,待定系数法,用轴对称解决最短路径问题是解本题的关键.
2.已知,如图,在平面直角坐标系xoy中,直线l1:y=x+3分别交x轴、y轴于点A、B两点,直线l2:y=﹣3x过原点且与直线l1相交于C,点P为y轴上一动点.
(1)求点C的坐标;
(2)在平面坐标系中是否存在点M,使以A、O、C、M为顶点的四边形为平行四边形.若存在,求出点M的坐标;若不存在,请说明理由;
(3)当PA+PC的值最小时,求此时点P的坐标,并求PA+PC的最小值.
【分析】(1)联立两直线解析式组成方程组,解得即可得出结论;
(2)利用平行四边形的对角线互相平分和中点坐标公式即可得出结论;
(3)先确定出点A关于y轴的对称点A',即可求出PA+PC的最小值,再用待定系数法求出直线A'C的解析式即可得出点P坐标.
【解答】解:(1)∵直线l1:y=x+3①与直线l2:y=﹣3x②相交于C,
联立①②解得,x=﹣,y=,
∴C(﹣,);
(2)∵直线y=x+3交x轴于点A,
∴A(﹣3,0),
由(1)知,C(﹣,),
∵以A、O、C、M为顶点的四边形为平行四边形,
设M(m,n)如图1,
∴①当AC是对角线时,(﹣3﹣)=m,(0+)=n,
∴m=﹣,n=,
∴M(﹣,),
②当OC是对角线时,(0﹣)=(﹣3+m),(0+)=(0+n),
∴m=,n=,
M1(,),
③当OA为对角线时,(0﹣3)=(m﹣),(0+0)=(m+),
∴m=﹣,n=﹣.
M2(﹣,),
(3)如图2,作点A(﹣3,0)关于y轴的对称点A'(3,0),
连接CA'交y轴于点P,此时,PC+PA最小,最小值为CA'==,
由(1)知,C(﹣,),
∵A'(3,0),
∴直线A'C的解析式为y=﹣x+,
∴P(0,).
【点评】此题是一次函数综合题,主要考查了函数图象的交点坐标的求法,平行四边形的性质,待定系数法,极值的确定,用分类讨论的思想和方程(组)解决问题是解本题的关键.
3.问题情境:
平面直角坐标系中,矩形纸片OBCD按如图的方式放置.已知OB=10,BC=6,将这张纸片沿过点B的直线折叠,使点O落在边CD上,记作点A,折痕与边OD交于点E.
数学探究:
(1)点C的坐标为 (10,6) ;
(2)求点E的坐标及直线BE的函数关系式;
(3)若点P是x轴上的一点,直线BE上是否存在点Q,能使以A,B,P,Q为顶点的四边形是平行四边形?若存在,直接写出相应的点Q的坐标;若不存在,说明理由.
【分析】(1)利用矩形的性质的出货∠OBC=90°,即可得出结论;
(2)先利用勾股定理求出AC=8,进而利用勾股定理求出OE,得出点E坐标,最后用待定系数法即可得出结论;
(3)先求出点A坐标,再分两种情况,利用平行四边形的性质建立方程求解即可得出结论.
【解答】解:(1)∵四边形OBCD是矩形,
∴∠OBC=90°,
∵OB=10,BC=6,
∴C(10,6),
故答案为:(10,6);
(2)∵四边形OBCD是矩形,
∴OB=CD=10,AD=BC=6,∠C=∠ODC=90°,
设OE=m,
∴DE=OD﹣OE=6﹣m,
由折叠知,AB=OB=10,AE=OE=m,
在Rt△ABC中,根据勾股定理得,AC==8,
∴AD=CD﹣AC=10﹣8=2,
在Rt△ADE中,根据勾股定理得,AD2+DE2=AE2,
∴22+(6﹣m)2=m2,
∴m=,
∴E(0,),
设直线BE的函数关系式为y=kx+,
∵B(10,0),
∴10k+=0,
∴k=﹣,
∴直线BE的函数关系式为y=﹣x+;
(3)存在,理由:由(2)知,AD=2,
∴A(2,6),
∵能使以A,B,P,Q为顶点的四边形是平行四边形,
∴PQ∥AB,
①当BQ为的对角线时,
∴AQ∥BP,
∵点B,P在x轴,
∴Q的纵坐标等于点A的纵坐标6,
∵点Q在直线BE:y=﹣x+上,
∴﹣x+=6,
∴x=﹣8,
∴Q(﹣8,6),
②当BQ为边时,
∴AQ与BP互相平分,
设Q(n,﹣n+),
∴[6+(﹣n+)]=0,
∴n=28,
∴Q(28,﹣6),
即:直线BE上是存在点Q,能使以A,B,P,Q为顶点的四边形是平行四边形,点Q(﹣8,6)或(28,﹣6).
【点评】此题是一次函数综合题,主要考查了待定系数法,平行四边形的性质,矩形的性质,用方程的思想解决问题是解本题的关键.
4.如图,在平面直角坐标系中,直线分别与x轴、y轴交于点B、C,且与直线交于点A.
(1)分别求出点A、B、C的坐标;
(2)若D是线段OA上的点,且△COD的面积为12,求直线CD的函数表达式;
(3)在(2)的条件下,设P是射线CD上的点,在平面内是否存在点Q,使以O、C、P、Q为顶点的四边形是菱形?若存在,直接写出点Q的坐标;若不存在,请说明理由.
【分析】(1)把x=0,y=0分别代入直线L1,即可求出y和x的值,即得到B、C的坐标,解由直线BC和直线OA的方程组即可求出A的坐标;
(2)设D(x,x),代入面积公式即可求出x,即得到D的坐标,设直线CD的函数表达式是y=kx+b,把C(0,6),D(4,2)代入即可求出直线CD的函数表达式;
(3)存在点Q,使以O、C、P、Q为顶点的四边形是菱形,根据菱形的性质能写出Q的坐标.
【解答】解:(1)直线,
当x=0时,y=6,
当y=0时,x=12,
∴B(12,0),C(0,6),
解方程组:得:,
∴A(6,3),
答:A(6,3),B(12,0),C(0,6).
(2)解:设D(x,x),
∵△COD的面积为12,
∴×6×x=12,
解得:x=4,
∴D(4,2),
设直线CD的函数表达式是y=kx+b,把C(0,6),D(4,2)代入得:
,
解得:,
∴y=﹣x+6,
答:直线CD的函数表达式是y=﹣x+6.
(3)答:存在点Q,如图,
使以O、C、P、Q为顶点的四边形是菱形,点Q的坐标是(6,6)或(﹣3,3)或.
【点评】本题主要考查了一次函数图象上点的坐标特征,用待定系数法求一次函数的解析式,解二元一次方程组,菱形的性质,三角形的面积等知识点,解此题的关键是熟练地运用知识进行计算.此题是一个综合性很强的题目.
5.如图,在直角坐标系中,OA=3,OC=4,点B是y轴上一动点,以AC为对角线作平行四边形ABCD.
(1)求直线AC的函数解析式;
(2)设点B(0,m),记平行四边形ABCD的面积为S,请写出S与m的函数关系式,并求当BD取得最小值时的S的值;
(3)当点B在y轴上运动,在使得平行四边形ABCD是菱形的同时,在x轴取一点P,使得△PAB是等腰三角形,请直接写出点P的坐标.
【分析】(1)根据OA、OC的长度结合图形可得出点A、C的坐标,再利用待定系数法即可求出直线AC的解析式;
(2)根据点B的坐标可得出BC的长度,结合平行四边形的面积公式即可得出S关于m的函数关系式,再根据AD∥y轴即可找出当BD最短时m的值,将其代入S关于m的函数关系式中即可得出结论;
(3)根据菱形的性质找出m的值,从而找出点B的坐标,设点P的坐标为(n,0),根据两点间的距离公式找出AP、BP、AB的长度,分AP=BP、AP=AB、BP=AB三种情况求出n值,再将其代入点P的坐标中即可得出结论.
【解答】解:(1)∵OA=3,OC=4,
∴A(﹣3,0)、C(0,4).
设直线AC的函数解析式为y=kx+b,
将点A(﹣3,0)、C(0,4)代入y=kx+b中,
得:,解得:,
∴直线AC的函数解析式为y=x+4.
(2)∵点B(0,m),四边形ABCD为以AC为对角线的平行四边形,
∴BC=|4﹣m|,
∴S=BC?OA=|﹣3m+12|(m≠4).
∵四边形ABCD为平行四边形,
∴AD∥BC,
∴当BD⊥y轴时,BD最小(如图1).
∵AD∥OB,AO⊥OB,DA⊥OB,
∴四边形AOBD为矩形,
∴AD=OB=BC,
∴点B为OC的中点,即m==2,
此时S=|﹣3×2+12|=6.
∴S与m的函数关系式为S=|﹣3m+12|(m≠4),当BD取得最小值时的S的值为6.
(3)∵平行四边形ABCD是菱形,
∴AB=BC.
∵AB==,BC=4﹣m,
∴=4﹣m,
解得:m=,
∴B(0,).
设点P的坐标为(n,0),
∵A(﹣3,0),B(0,),
∴PA=|n+3|,PB=,AB=4﹣=.
△PAB是等腰三角形分三种情况:
①当PA=PB时,有|n+3|=,
解得:n=﹣,
此时点P的坐标为(﹣,0);
②当PA=AB时,有|n+3|=,
解得:n1=,n2=﹣,
此时点P的坐标为(﹣,0)或(,0);
③当PB=AB时,有=,
解得:n3=﹣3(舍去),n4=3,
此时点P的坐标为(3,0).
综上可知:点P的坐标为(﹣,0)、(﹣,0)、(,0)或(3,0).
【点评】本题考查了待定系数法求函数解析式、平行四边形的性质、菱形的性质以及等腰三角形的性质,解题的关键是:(1)利用待定系数法求出函数解析式;(2)根据平行四边形的面积公式找出S关于m的函数关系式;(3)分三种情况讨论.本题属于中档题,难度不大,解决该题型题目时,熟练掌握多边形的性质是关键.
6.已知:如图,已知直线AB的函数解析式为y=﹣2x+8,与x轴交于点A,与y轴交于点B.
(1)求A、B两点的坐标;
(2)若点P(m,n)为线段AB上的一个动点(与A、B不重合),作PE⊥x轴于点E,PF⊥y轴于点F,连接EF,问:
①若△PAO的面积为S,求S关于m的函数关系式,并写出m的取值范围;
②是否存在点P,使EF的值最小?若存在,求出EF的最小值;若不存在,请说明理由.
【分析】(1)利用待定系数法即可解决问题;
(2)①连接OP,根据三角形的面积公式S△PAO=×OA×PE计算即可;
②存在,首先证明四边形OEPF是矩形,可得EF=OP,根据垂线段最短可知:当OP⊥AB时,此时EF最小;
【解答】解:(1)令x=0,则y=8,
∴B(0,8),
令y=0,则﹣2x+8=0,
∴x=4,
∴A(4,0),
(2)①连接OP.
∵点P(m,n)为线段AB上的一个动点,
∴﹣2m+8=n,∵A(4,0),
∴OA=4,
∴0<m<4
∴S△PAO=×OA×PE=×4×n=2(﹣2m+8)=﹣4m+16,(0<m<4);
②存在,
理由:∵PE⊥x轴于点E,PF⊥y轴于点F,OA⊥OB,
∴四边形OEPF是矩形,
∴EF=OP,
当OP⊥AB时,此时EF最小,
∵A(4,0),B(0,8),
∴AB=4
∵S△AOB=×OA×OB=×AB×OP,
∴OP===,
∴EF的最小值=OP=.
【点评】本题考查一次函数的性质、矩形的性质、三角形的面积等知识,解题的关键是学会用转化的思想思考问题,属于中考常考题型.
7.如图,在平面直角坐标系中,直线y=2x+4与坐标轴分别交于A、B两点,点C在x轴上,且OA=OC,点P从A出发沿射线AC方向运动,速度为每秒1个单位长度,设运动时间为t(s).
(1)求点B、C的坐标;
(2)若△OCP的面积为4,求运动时间t的值;
(3)如图2,若∠POQ=90°,且OP=OQ,连接BQ,求运动过程中BQ的最小值.
【分析】(1)在y=2x+4中分别令x=0和y=0,则可求得A、B坐标,结合OA=OC可求得C点坐标;
(2)由条件可求得点O到直线AC的距离,用t可表示出PC的长,则可表示出△OCP的面积,可得到关于t的方程,可求得t的值;
(3)连接AQ,可证明△OQA≌△OPC,则可知∠OAQ=45°,可求得直线AQ的解析式,设直线AQ交x轴于点E,则当BQ⊥AE时,BQ最短,可求得BQ的长.
【解答】解:
(1)在y=2x+4中,令x=0可得y=4,令y=0可得2x+4=0,解得x=﹣2,
∴A(0,4),B(,0),
∴OC=OA=4,
∴C(,0);
(2)∵OA=OC=4,
∴AC=8,
∴点O到直线AC的距离为4,
当运动t秒时,则AP=t,则CP=|AP﹣AC|=|t﹣8|,
∴S△OCP=×4|t﹣8|=2|t﹣8|,
∵△OCP的面积为4,
∴2|t﹣8|=4,解得t=6或t=10,
即当t为6秒或10秒时,△OCP的面积为4;
(3)如图,连接AQ,
∵∠POQ=90°,∠AOC=90°,
∴∠QOA+∠AOP=∠AOP+∠POC,
∴∠AOQ=∠COP,
在△OQA和△OPC中
∴△OQA≌△OPC(SAS),
∴∠OCP=∠OAQ=45°,
设直线AQ交x轴于点E,则E(﹣4,0),
∴BE=2,
设直线AQ解析式为y=kx+b,
∴,解得,
∴直线AQ解析式为y=x+4,
∴点Q始终在直线上,
∴BQ⊥AE时,BQ最短,
此时BQ=2,即BQ的最小值为2.
【点评】本题为一次函数的综合应用,涉及函数与坐标轴的交点、三角形的面积、全等三角形的判定和性质、待定系数法、最短距离及方程思想等知识.在(2)中用t表示出△OCP的面积是解题的关键,在(3)中确定出点Q的位置是解题的关键.本题考查知识点较多,综合性较强,难度适中.
8.如图,矩形OABC放在以O为原点的平面直角坐标系中,A(3,0),C(0,2),点E是AB的中点,点F在BC边上,且CF=1.
(1)点E的坐标为 (3,1) ,点F的坐标为 (1,2) ;
(2)点E关于x轴的对称点为E′,点F关于y轴的对称点为F′,
①点E′的坐标为 (3,﹣1) ,点F′的坐标为 (﹣1,2) ;
②求直线E′F′的解析式;
(3)若M为x轴上的动点,N为y轴上的动点,当四边形MNFE的周长最小时,求出点M,N的坐标,并求出周长的最小值.
【分析】(1)先求出OA,OC,再根据矩形的性质得出BA=2,即可得出结论;
(2)①利用对称的性质即可得出结论;
②利用待定系数法即可求出直线E'F'解析式;
(3)先判断出点M,N是直线E'F'和x,y轴的交点,再利用两点间的距离公式即可得出结论.
【解答】解:(1)∵A(3,0),B(0,2),
∴OA=3,OC=2,
∵四边形OABC是矩形,
∴BC∥OA,OC∥AB,BC=OA=3,AB=OC=2,
∴C(3,2),
∵点E是AB的中点,
∴AE=AB=1,
∴E(3,1),
∵点F在BC上,且CF=1,
∴F(1,2),
故答案为:(3,1),(1,2),
(2)①由(1)知,E(3,1),F(1,2),
∵点E关于x轴的对称点为E′,点F关于y轴的对称点为F′,
∴E'(3,﹣1),F'(﹣1,2),
故答案为:(3,﹣1),F'(﹣1,2);
②设直线E'F'的解析式为y=kx+b,
∴,
∴,
∴直线E'F'的解析式为y=﹣x+;
(3)如图,∵E(3,1),F(1,2),
∴EF=,
∵点E关于x轴的对称点为E′,点F关于y轴的对称点为F′,
∴连接E'F'和x轴交于M,和y轴交于N,此时四边形MNFE的周长最小,
∴NF=NF',ME=ME',
∵E'(3,﹣1),F'(﹣1,2),
∴E'F==5,
∴四边形MNFE的周长的最小值为NF+MN+ME+EF
=NF'+MN+ME'+EF=E'F'+EF=5+.
【点评】此题是四边形综合题,主要考查了矩形的性质,对称的性质,待定系数法,两点间的距离公式,解(2)的关键是求出点E',F'的坐标,解(3)的关键是判断出点M,N的位置,是一道常规题.
9.如图,在平面直角坐标系中,过点B(6,0)的直线AB与直线OA相交于点A(4,2),动点M沿路线O→A→C运动.
(1)求直线AB的解析式.
(2)求△OAC的面积.
(3)当△OMC的面积是△OAC的面积的时,求出这时点M的坐标.
【分析】(1)利用待定系数法即可求得函数的解析式;
(2)求得C的坐标,即OC的长,利用三角形的面积公式即可求解;
(3)当△OMC的面积是△OAC的面积的时,根据面积公式即可求得M的横坐标,然后代入解析式即可求得M的坐标.
【解答】解:(1)设直线AB的解析式是y=kx+b,
根据题意得:,
解得:,
则直线的解析式是:y=﹣x+6;
(2)在y=﹣x+6中,令x=0,解得:y=6,
S△OAC=×6×4=12;
(3)设OA的解析式是y=mx,则4m=2,
解得:m=,
则直线的解析式是:y=x,
∵当△OMC的面积是△OAC的面积的时,
∴M的横坐标是×4=1,
在y=x中,当x=1时,y=,则M的坐标是(1,);
在y=﹣x+6中,x=1则y=5,则M的坐标是(1,5).
则M的坐标是:M1(1,)或M2(1,5).
【点评】本题主要考查了用待定系数法求函数的解析式.先根据条件列出关于字母系数的方程,解方程求解即可得到函数解析式.当已知函数解析式时,求函数中字母的值就是求关于字母系数的方程的解.
10.如图1,已知直线y=2x+2与y轴、x轴分别交于A、B两点,以B为直角顶点在第二象限作等腰Rt△ABC.
(1)求点C的坐标,并求出直线AC的关系式.
(2)如图2,直线CB交y轴于E,在直线CB上取一点D,连接AD,若AD=AC,求证:BE=DE.
(3)如图3,在(1)的条件下,直线AC交x轴于M,P(,k)是线段BC上一点,在线段BM上是否存在一点N,使直线PN平分△BCM的面积?若存在,请求出点N的坐标;若不存在,请说明理由.
【分析】(1)如图1,作CQ⊥x轴,垂足为Q,利用等腰直角三角形的性质证明△ABO≌△BCQ,根据全等三角形的性质求OQ,CQ的长,确定C点坐标;
(2)同(1)的方法证明△BCH≌△BDF,再根据线段的相等关系证明△BOE≌△DGE,得出结论;
(3)依题意确定P点坐标,可知△BPN中BN边上的高,再由S△PBN=S△BCM,求BN,进而得出ON.
【解答】解:(1)如图1,作CQ⊥x轴,垂足为Q,
∵∠OBA+∠OAB=90°,∠OBA+∠QBC=90°,
∴∠OAB=∠QBC,
又∵AB=BC,∠AOB=∠CQB=90°,
∴△ABO≌△BCQ,
∴BQ=AO=2,OQ=BQ+BO=3,CQ=OB=1,
∴C(﹣3,1),
由A(0,2),C(﹣3,1)可知,直线AC:y=x+2;
(2)如图2,作CH⊥x轴于H,DF⊥x轴于F,DG⊥y轴于G,
∵AC=AD,AB⊥CB,
∴BC=BD,
∴△BCH≌△BDF,
∴BF=BH=2,
∴OF=OB=1,
∴DG=OB,
∴△BOE≌△DGE,
∴BE=DE;
(3)如图3,直线BC:y=﹣x﹣,P(,k)是线段BC上一点,
∴P(﹣,),
由y=x+2知M(﹣6,0),
∴BM=5,则S△BCM=.
假设存在点N使直线PN平分△BCM的面积,
则BN?=×,
∴BN=,ON=,
∵BN<BM,
∴点N在线段BM上,
∴N(﹣,0).
【点评】本题考查了一次函数的综合运用.关键是根据等腰直角三角形的特殊性证明全等三角形,利用全等三角形的性质求解.
11.【背景知识】研究平面直角坐标系,我们可以发现一条重要的规律:若平面直角坐标系上有两个不同的点A(xA,yA)、B(xB,yB),则线段AB的中点坐标可以表示为(,).
【简单应用】如图1,直线AB与y轴交于点A(0,3),与x轴交于点B(4,0),过原点O的直线L将△ABO分成面积相等的两部分,请求出直线L的解析式;
【探究升级】小明发现“若四边形一条对角线平分四边形的面积,则这条对角线必经过另一条对角线的中点”
如图2,在四边形ABCD中,对角线AC、BD相交于点O,S△ABD=S△BCD.试说明AO=CO;
【综合运用】如图3,在平面直角坐标系中A(1,4),B(3,﹣2),C(2m,﹣m+5),若OC恰好平分四边形OACB的面积,求点C的坐标.
【分析】【简单应用】先判断出直线L过线段AB的中点,再求出线段AB的中点,最后用待定系数法即可得出结论;
【探究升级】先判断出AF=CG,进而判断出△AOF≌△COG,即可得出结论;
【综合运用】借助【探究升级】的结论判断出直线OC过线段AB的中点,进而求出直线OC的解析式,最后将点C坐标代入即可得出结论.
【解答】解:【简单应用】:∵直线L将△ABO分成面积相等的两部分,
∴直线L必过相等AB的中点,
设线段AB的中点为E,
∵A(0,3),B(4,0),
∴E(,),
∴E(2,),
∵直线L过原点,
∴设直线L的解析式为y=kx,
∴2k=,
∴k=,
∴直线L的解析式为y=x;
【探究升级】:如图2,
过点A作AF⊥BD于F,过点C作CG⊥BD于G,
∴S△ABD=BD?AF,S△CBD=BD?CG,
∵S△ABD=S△BCD,
∴BD?AF=BD?CG,
∴AF=CG,
在△AOF和△COG中,,
∴△AOF≌△COG(AAS),
∴OA=OC;
【综合运用】:如图3,
由【探究升级】知,若四边形一条对角线平分四边形的面积,则这条对角线必经过另一条对角线的中点,
∵OC恰好平分四边形OACB的面积,
∴OC过四边形OACB的对角线OA的中点,
连接AB,设线段AB的中点为H,
∵A(1,4),B(3,﹣2),
∴H(2,1),设直线OC的解析式为y=k'x,
∴2k'=1,
∴k'=,
∴直线OC的解析式为y=x,
∵点C(2m,﹣m+5)在直线OC上,
∴﹣m+5=×2m,
∴m=,
∴C(5,).
【点评】此题是一次函数综合题,主要考查了待定系数法,三角形的中线的性质,全等三角形的判定和性质,构造出全等三角形是解本题的关键.
12.如图,四边形ABCD是正方形,E是边AB上一点,连接DE,将直线DE绕点D逆时针旋转90°,交BC的延长线于点F
(1)如图1,求证:DE=DF;
(2)如图2,连接EF,若D关于直线EF的对称点为H,连接CH,过点H作PH⊥CH交AB于点P,求证:E是AP的中点;
(3)如图3,在(2)的条件下,连接AC交EF于点G,连接BG、BH,若BG=2,AB=6,求线段PH的长.
【分析】(1)由正方形的性质可得AB=AD=CD,∠A=∠ADC=90°=∠BCD,由“SAS”可证△ADE≌△CDF,可得DE=DF;
(2)如图2,连接EH,FH,由轴对称性质可得EH=DE=FH=DF,由余角的性质和三角形内角和定理可得∠EPH=∠HCF,∠EHP=∠CHF,由“ASA”可证△EHP≌△FHC,可得PE=CF,即可得结论;
(3)如图3,连接PC,EH,FH,过点E作EK∥BC,交AC于K,由正方形的性质和平行线的性质可得∠AKE=∠ACB=45°=∠EAK,∠AEK=∠ABC=90°,∠EKG=∠GCF,由“AAS”可证△EKG≌△FCG,可得EG=FG,由直角三角形的性质可得EG=GF=BG=2,由勾股定理可求BP的长,PC的长,由等腰直角三角形的性质可求PH的长.
【解答】证明:(1)∵四边形ABCD是正方形,
∴AB=AD=CD,∠A=∠ADC=90°=∠BCD,
∵将直线DE绕点D逆时针旋转90°,
∴∠EDF=90°,
∴∠ADC=∠EDF,
∴∠ADE=∠CDF,且AD=CD,∠A=∠DCF=90°,
∴△ADE≌△CDF(SAS),
∴DE=DF,
(2)如图2,连接EH,FH,
∵点D关于直线EF的对称点为H,
∴EH=DE,FH=DF,且DE=DF,
∴EH=DE=FH=DF,
∵DE=EH,DF=HF,EF=EF,
∴△DEF≌△HEF(SSS)
∴∠EHF=∠EDF=90°,且PH⊥CH,
∴∠PHE=∠FHC,
∵∠B=∠PHC=90°,∠BGP=∠CGH,
∴∠BPG=∠HCG,
∴∠EPH=∠HCF,且EH=HF,∠EHP=∠CHF,
∴△EHP≌△FHC(AAS)
∴EP=CF,
∵△ADE≌△CDF,
∴AE=CF,
∴AE=EP,
∴点E是AP中点,
(3)如图3,连接PC,EH,FH,过点E作EK∥BC,交AC于K,
∵EK∥BC,
∴∠AKE=∠ACB=45°=∠EAK,∠AEK=∠ABC=90°,∠EKG=∠GCF,
∴AE=EK,
∵AE=CF,
∴EK=CF,且∠EKG=∠GCF,∠EGK=∠CGF,
∴△EKG≌△FCG(AAS)
∴EG=FG,
∵BG=2,
∴EG=FG=BG=2,
∴EF=4,
∵EF2=BE2+BF2,
∴80=(6﹣AE)2+(6+AE)2,
∴AE=2
∴BP=AB﹣AE﹣EP=2
∴PC===2
由(2)可知△EHP≌△FHC,
∴PH=CH,且PH⊥CH
∴PC=PH
∴PH=2
【点评】本题是四边形综合题,考查了正方形的性质,全等三角形的判定和性质,直角三角形的性质,勾股定理等知识,添加恰当辅助线构造全等三角形是本题的关键.
13.如图,四边形ABCD是正方形,E是边AB上一点,连接DE,直线DE绕着点D逆时针旋转90°,交BC的延长线于点F.
(1)如图1,求证:DE=DF;
(2)如图2,连接EF,若D关于直线EF的对称点为H,连接CH,过点H作PH⊥CH交AB于点P,求证:E为AP中点;
(3)如图3,在(2)的条件下,连接AC交EF于点G,连接BG,BH,若BG=,AB=3,求线段PH的长.
【分析】(1)全等三角形是证明两条线段相等的重要方法之一.只要证明△ADE≌△CDF,即可得到DE=DF;
(2)连接HE,HF,由点H与点D关于直线EF对称,所以EH=ED,FH=FD.因为DE=DF,所以EH=FH=ED=FD.即四边形DEHF是菱形.由∠EDF=90°,得到四边形DEHF是正方形,利用正方形的性质证明△HPE≌△HCF,得到PE=CF,所以AE=PE,得到点E是AP的中点;
(3)过点E作EK∥BF,只要证明△EGK≌△CFG,可得EG=GF,推出EF=2BG=2,设AE=CF=a
则BE=3﹣a,BF=3+a,可得(3﹣a)2+(3+a)2=(2
)2,再证明△PCH是等腰直角三角形,求出PC即可解决问题;
【解答】证明:(1)∵直线DE绕着点D逆时针旋转90°,
∴∠EDF=90°,
∵四边形ABCD是正方形,
∴∠ADC=∠A=∠DCB=90°,AD=DC
∴∠ADC=∠EDF=∠DCF=∠A=90°,
∴∠ADC﹣∠EDC=∠EDF﹣∠EDC,
即∠ADE=∠CDF,
在△ADE与△CDF中,
,
∴△ADE≌△CDF(ASA),
∴DE=DF;
(2)连接EH,FH,如图2
∵D、H关于EF对称,
∴EF垂直平分DH,
∴HE=DE,DF=HF,
又∵EF=EF,
∴△EDF≌△EHF,
∴∠EHF=∠EDF=90°,
又∵∠B=∠EHF=90°,
∴∠BPH=∠BCH,
∴∠EPH=∠FCH,
又∵DE=DF,
∴EH=HF,
又∵PH⊥CH,
∴∠PHC=∠EHF=90°,
∴∠PHE=∠CHF,
∴△PEH≌△CFH,
∴CF=PE,
又∵△ADE≌△CDF
∴AE=CF,
∴AE=PE,
∴E为AP中点;
(3)过点E作EK∥BF,如图3:
∵EK∥BF,
∴∠EKA=∠BCA=45°,∠EKG=∠FCG,
∴∠EAK=∠EKA=45°,
∴EA=EK=CF,
又∵∠EGK=∠CGF,
∴△EGK≌△CFG,
∴EG=GF,
∴在Rt△EBF中,EF=2BG=2
,
∴设AE=CF=a
则BE=3﹣a,BF=3+a,
∴(3﹣a)2+(3+a)2=(2
)2
∴a=1(a=﹣1舍),
∴AE=PE=1,
∴BP=1,
连接PC,
∴PC==,
由(2)可知△PEH≌△CFH,
∴HP=HC,∠PHE=∠CHF,
∴∠PHC=∠EHF=90°,
∴△PCH是等腰直角三角形,
∴PH=HC=×=.
【点评】本题考查了正方形的性质,全等三角形的判定定理和性质定理,勾股定理的应用,对称的性质,等腰直角三角形的性质等知识,解决本题的关键是利用正方形的性质得到相等的边和相等的角,证明三角形全等,作出辅助线也是解决本题的关键.
14.如图1,在△ABC中,∠ACB为锐角,点D为射线BC上一点,联结AD,以AD为一边且在AD的右侧作正方形ADEF.
(1)如果AB=AC,∠BAC=90°,
①当点D在线段BC上时(与点B不重合),如图2,将△ABD绕A点逆时针旋转90°,所得到的三角形为 △ACF ,线段CF、BD所在直线的位置关系为 互相垂直 ,线段CF、BD的数量关系为 相等 ;
②当点D在线段BC的延长线上时,如图3,①中的结论是否仍然成立,并说明理由;
(2)如果AB≠AC,∠BAC是锐角,点D在线段BC上,当∠ACB满足什么条件时,CF⊥BC(点C、F不重合),并说明理由.
【分析】(1)①当点D在线段BC上时,根据等腰直角三角形的性质以及旋转的性质,即可得出CF=BD,BD⊥CF;②当点D在BC的延长线上时,①的结论仍成立.由正方形ADEF的性质可推出△DAB≌△FAC,所以CF=BD,∠ACF=∠ABD,结合∠BAC=90°,AB=AC,得到∠BCF=∠ACB+∠ACF=90°,即CF⊥BD;
(2)当∠ACB=45°时,过点A作AG⊥AC交CB的延长线于点G,则∠GAC=90°,可推出∠ACB=∠AGC,所以AC=AG,由(1)①中的方法可得CF⊥BD.
【解答】解:(1)①如图2所示,将△ABD绕A点逆时针旋转90°,所得到△ACF,则
由旋转的性质可得:∠ACF=∠B,CF=BD,
∵AB=AC,∠BAC=90°,
∴∠B=∠ACB=45°=∠ACF,
∴∠BCF=90°,即BD⊥CF;
故答案为:△ACF,垂直,相等;
②如图3所示,当点D在BC的延长线上时,①中的结论仍成立.
证明:由正方形ADEF得,AD=AF,∠DAF=90°.
∵∠BAC=90°
∴∠DAF=∠BAC,
∴∠DAB=∠FAC,
又∵AB=AC,
∴△DAB≌△FAC(SAS),
∴CF=BD,∠ACF=∠ABD.
∵∠BAC=90°,AB=AC,
∴∠ABC=45°,
∴∠ACF=45°,
∴∠BCF=∠ACB+∠ACF=90°,即
CF⊥BD;
(2)如图4所示,当∠ACB=45°时,CF⊥BD.
理由:过点A作AG⊥AC交CB或CB的延长线于点G,则∠GAC=90°,
∵∠ACB=45°,∠AGC=90°﹣∠ACB=45°,
∴∠ACB=∠AGC,
∴AC=AG,
又∵∠DAG=∠FAC(同角的余角相等),AD=AF,
∴△GAD≌△CAF(SAS),
∴∠ACF=∠AGC=45°,
∴∠BCF=∠ACB+∠ACF=45°+45°=90°,即CF⊥BC.
【点评】本题主要考查正方形的性质,余角的性质,三角形全等的判定和直角三角形的判定,判定两个三角形全等,先根据已知条件或求证的结论确定三角形,然后再根据三角形全等的判定方法,看缺什么条件,再去证什么条件.解题的关键是过点A作AG⊥AC交CB的延长线于点G,构造全等三角形.
15.如图,正方形ABCD中,AC是对角线,今有较大的直角三角板,一边始终经过点B,直角顶点P在射线AC上移动,另一边交DC于Q.
(1)如图1,当点Q在DC边上时,猜想并写出PB与PQ所满足的数量关系;并加以证明;
(2)如图2,当点Q落在DC的延长线上时,猜想并写出PB与PQ满足的数量关系,请证明你的猜想.
【分析】(1)过P作PE⊥BC,PF⊥CD,证明Rt△PQF≌Rt△PBE,即可;
(2)证明思路同(1)
【解答】(1)PB=PQ,
证明:过P作PE⊥BC,PF⊥CD,
∵P,C为正方形对角线AC上的点,
∴PC平分∠DCB,∠DCB=90°,
∴PF=PE,
∴四边形PECF为正方形,
∵∠BPE+∠QPE=90°,∠QPE+∠QPF=90°,
∴∠BPE=∠QPF,
∴Rt△PQF≌Rt△PBE,
∴PB=PQ;
(2)PB=PQ,
证明:过P作PE⊥BC,PF⊥CD,
∵P,C为正方形对角线AC上的点,
∴PC平分∠DCB,∠DCB=90°,
∴PF=PE,
∴四边形PECF为正方形,
∵∠BPF+∠QPF=90°,∠BPF+∠BPE=90°,
∴∠BPE=∠QPF,
∴Rt△PQF≌Rt△PBE,
∴PB=PQ.
【点评】此题考查了正方形,角平分线的性质,以及全等三角形判定与性质.此题综合性较强,注意数形结合思想.
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
