浙教八下数学同步检测卷:特殊平行四边形(含答案)
文档属性
| 名称 | 浙教八下数学同步检测卷:特殊平行四边形(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-26 13:33:22 | ||
图片预览




文档简介
浙教八下数学单元检测题
特殊四边形(含答案)
单选题(每小题3分,共30分)
1.正方形的边长与对角线之比是(
)
A.1∶2
B.∶2
C.2∶3
D.2∶1
2.下列命题中,真命题是( )
A.对角线互相平分且相等的四边形是矩形B.对角线互相垂直且相等的四边形是矩形
C.对角线互相平分且相等的四边形是菱形D.对角线互相垂直且相等的四边形是菱形
3.矩形具有而菱形不具有的性质是(
)
A.对边平行且相等
B.对角线垂直
C.对角线互相平分
D.对角线相等
4.如图,在正方形
中,
是
上的一点,且
,则
的度数是(
)
A.
B.
C.
D.
5.如图,点P是菱形ABCD对角线BD上一点,PE⊥AB于点E,且PE=2.连接PC,若菱形的周长为24.则△BCP的面积为(
)
A.4
B.6
C.8
D.12
6.已知四边形ABCD是平行四边形,对角线AC与BD相交于点O,下列结论中不正确的是( )
A.当AD=DC时,四边形ABCD是菱形
B.当AB2=OA2+OB2时,四边形ABCD是菱形
C.当OA=OB时,四边形ABCD是矩形
D.当∠ABD=∠CBD时,四边形ABCD是矩形
7.如图,每个小正方形的边长为l,在△ABC中,点D为AB的中点,则线段CD的长为(
)
A.
B.
C.
D.
8.如图,在?ABCD中,E为BC边上一点,以AE为边作正方形AEFG,若∠BAE=45°,∠CEF=15°,则∠D的度数是( )
A.55°
B.60°
C.65°
D.70°
9.如图,矩形中,,.点、点分别在边、上,点、在对角线
上.若四边形是菱形,则的长为(
).
A.
B.
C.
D.
10.如图,在平面直角坐标系xOy中,菱形ABCD的顶点A的坐标为(2,0),点B的坐标为(0,1),点C在第一象限,对角线BD与x轴平行.直线y=x+3与x轴、y轴分别交于点E、F,将菱形ABCD沿x轴向左平移m个单位,当点D落在△EOF的内部时(不包括三角形的边),m的取值范围是( )
A.4<m<6
B.4≤m≤6
C.4<m<5
D.4≤m<5
二、填空题(每小题3分,共18分)
11.已知正方形的边长为,其周长为________.
12.如图,在菱形ABCD中,过点C作CEBC交对角线BD
于点
E
,若ECD20
,则ADB____________.
13.如图所示,在四边形ABCD中,对角线AC与BD相交于点O,AD∥BC,∠BAD=∠DCB,若不增加任何字母和辅助线,要使得四边形ABCD是矩形,则还需要增加一个条件____
14.如图,G是△ABC的重心,直线l过A点与BC平行.若直线CG分别与AB,直线l交于点D,E两点,直线BG与AC交于F点,则△AED的面积∶四边形ADGF的面积=_________________.
15.如图,顺次连结四边形ABCD四边的中点E、F、G、H,则四边形EFGH的形状一定是____.
16.如图矩形中,AB=8cm,BC=4cm,是的中点,,则四边形的面积为________cm2.
17.如图,正方形ABCD的边长为8,E为AD上一点.
若BE=10,则CE=__________.
18.点P是菱形ABCD的对角线AC上的一个动点,已知AB=1,∠ADC=120°,
点M,N分别是AB,BC边上的中点,则△MPN的周长最小值是______.
三、解答题(共52分)
19.如图,在矩形ABCD,AD=AE,DF⊥AE于点F.求证:AB=DF.
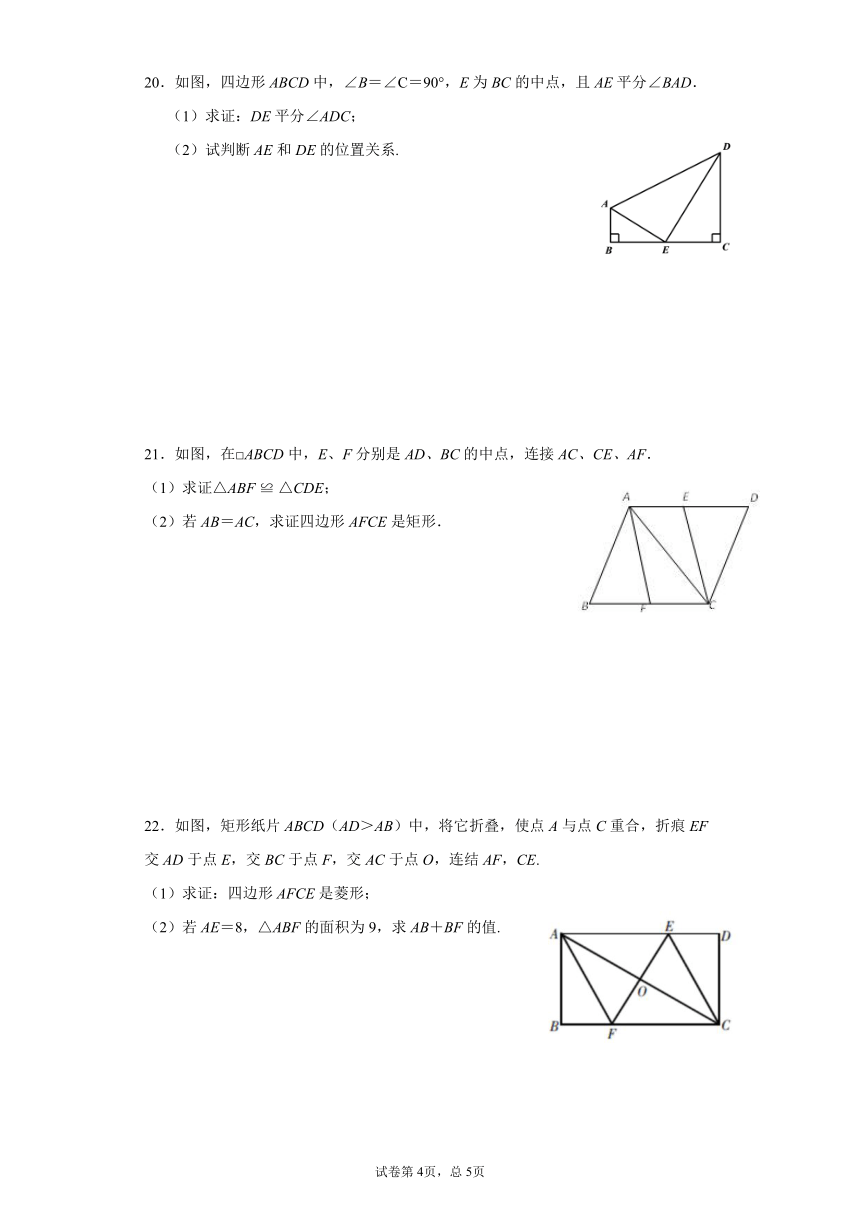
20.如图,四边形ABCD中,∠B=∠C=90°,E为BC的中点,且AE平分∠BAD.
(1)求证:DE平分∠ADC;
(2)试判断AE和DE的位置关系.
21.如图,在□ABCD中,E、F分别是AD、BC的中点,连接AC、CE、AF.
(1)求证△ABF
≌
△CDE;
(2)若AB=AC,求证四边形AFCE是矩形.
22.如图,矩形纸片ABCD(AD>AB)中,将它折叠,使点A与点C重合,折痕EF交AD于点E,交BC于点F,交AC于点O,连结AF,CE.
(1)求证:四边形AFCE是菱形;
(2)若AE=8,△ABF的面积为9,求AB+BF的值.
23.如图,平面直角坐标中,把矩形OABC沿对角线OB所在的直线折叠,点A落在点D处,OD与BC交于点E.OA、OC的长是关于x的一元二次方程x2﹣9x+18=0的两个根(OA>OC).
(1)求A、C的坐标.
(2)直接写出点E的坐标,并求出过点A、E的直线函数关系式.
(3)点F是x轴上一点,在坐标平面内是否存在点P,使以点O、B、P、F为顶点的四边形为菱形?若存在请直接写出P点坐标;若不存在,请说明理由.
24.如图,现有一张边长为4的正方形纸片ABCD,点P为AD边上的一点,将正方形纸片折叠,使点B落在点P处,点C落在点G处,PG交DC于点H,折痕为EF,连接BP,BH.
(1)求证:∠APB=∠BPH;
(2)当点P在边AD上移动(不与点A、点D重合)时,⊿PDH的周长是否发生变化?请证明你的结论.
参考答案
1.B
2.A
3.D
4.B
5.B
6.D
7.A
8.B
9.D
10.A
11.
12.35°
13.AC=BD或∠BAD=90°(答案不唯一)
14.3:2
15.平行四边形
16.10
17.2
18..
19.∵四边形ABCD是矩形,∴AD∥BC,∠B=90°,∴∠AEB=∠DAE.
∵DF⊥AE,∴∠AFD=∠B=90°.在△ABE和△DFA中,
∵
∴△ABE≌△DFA,∴AB=DF.
点睛:本题考查了全等三角形的判定与性质、矩形的性质的知识,属于基础题,难度不是很大,熟练掌握全等三角形的判定与性质是关键.
20..如图作EF∥AB∥CD,
∵AE平分∠BAD,
∴∠BAE=∠FAE=∠AEF,
∴AF=FE.
又∵点E为BC中点,
∴F为AD中点,
∴AF=FE=FD,
∴∠FDE=∠FED=∠EDC,
∴DE平分∠ADC.
(2)由(1)易知AE与DE垂直.
21.(1)∵
四边形ABCD是平行四边形,∴
AB=CD,AD=BC,∠B=∠D.
∵
E、F分别是AD、BC的中点,
∴
DE=AE=
AD,
BF=CF=
BC.∴
BF=DE,CF=AE.
∴
△ABF≌△CDE(SAS).
(2)∵△ABF≌△CDE(SAS),
∴
AF=CE.
又∵CF=AE,
∴四边形AFCE是平行四边形.
∵AB=AC,
F分别是BC的中点,
∴AF⊥BC.
即∠AFC=90°.
∴四边形AFCE是矩形.
22.
(1)证明:当顶点A与C重合时,折痕EF垂直平分AC,
∴OA=OC,∠AOE=∠COF=90°,
∵在矩形ABCD中,AD∥BC,
∴∠EAO=∠FCO,
∴△AOE≌△COF(ASA),
∴OE=OF,
∴四边形AFCE是平行四边形,
又∵EA=EC
∴平行四边形AFCE是菱形.
(2)∵四边形AFCE是菱形,
∴AF=AE=8,在Rt△ABF中,AB2+BF2=AF2,
∴AB2+BF2=64,∴(AB+BF)2-2AB·BF=64①,
∵△ABF的面积为9,
∴AB·BF=9,
∴AB·BF=18②,
由①、②得:(AB+BF)2=100,
∵AB+BF>0,
∴AB+BF=10.
23.(1)A(6,0),C(0,3);(2)E(,3),y=﹣x+;(3)满足条件的点P坐标为(6﹣3,3)或(6+3,3)或(,3)或(6,﹣3).
(1)由x2﹣9x+18=0可得x=3或6,
∵OA、OC的长是关于x的一元二次方程x2﹣9x+18=0的两个根(OA>OC),
∴OA=6,OC=3,
∴A(6,0),C(0,3).
(2)如图1中,
∵OA∥BC,
∴∠EBC=∠AOB,
根据翻折不变性可知:∠EOB=∠AOB,
∴∠EOB=∠EBO,
∴EO=EB,设EO=EB=x,
在Rt△ECO中,∵EO2=OC2+CE2,
∴x2=32+(6﹣x)2,
解得x=,
∴CE=BC﹣EB=6﹣=,
∴E(,3),
设直线AE的解析式为y=kx+b,则有,
解得,
∴直线AE的函数解析式为y=﹣x+.
(3)如图,OB==3.
①当OB为菱形的边时,OF1=OB=BP1=3=,故P1(6﹣3,3),
OF3=P3F3=BP3=3,故P3(6+3,3).
②当OB为菱形的对角线时,∵直线OB的解析式为y=x,
∴线段OB的垂直平分线的解析式为y=﹣2x+,
可得P2(,3),
③当OF4问问对角线时,可得P4(6,﹣3)
综上所述,满足条件的点P坐标为(6﹣3,3)或(6+3,3)或(,3)或(6,﹣3).
24.
(1)由折叠的性质,得,,
∴,
∴,
即.
∵,
∴,
∴.
(2)的周长不变.证明如下:
过点作,垂足为.
由(1)知.
在和中,
∴,
∴,.
∵,
∴.
在和中,
∴,
∴.
∴的周长为.
故的周长不发生变化.
【点睛】
考查了翻折变换的性质以及全等三角形的判定与性质和勾股定理、二次函数的最值问题等知识,熟练利用全等三角形的判定得出对应相等关系是解题关键.
第4题图
第5题图
第7题图
第8题图
第9题图
第10题图
第12题图
第13题图
第14题图
第15题图
第16题图
第17题图
第18题图
试卷第1页,总3页
试卷第1页,总3页
特殊四边形(含答案)
单选题(每小题3分,共30分)
1.正方形的边长与对角线之比是(
)
A.1∶2
B.∶2
C.2∶3
D.2∶1
2.下列命题中,真命题是( )
A.对角线互相平分且相等的四边形是矩形B.对角线互相垂直且相等的四边形是矩形
C.对角线互相平分且相等的四边形是菱形D.对角线互相垂直且相等的四边形是菱形
3.矩形具有而菱形不具有的性质是(
)
A.对边平行且相等
B.对角线垂直
C.对角线互相平分
D.对角线相等
4.如图,在正方形
中,
是
上的一点,且
,则
的度数是(
)
A.
B.
C.
D.
5.如图,点P是菱形ABCD对角线BD上一点,PE⊥AB于点E,且PE=2.连接PC,若菱形的周长为24.则△BCP的面积为(
)
A.4
B.6
C.8
D.12
6.已知四边形ABCD是平行四边形,对角线AC与BD相交于点O,下列结论中不正确的是( )
A.当AD=DC时,四边形ABCD是菱形
B.当AB2=OA2+OB2时,四边形ABCD是菱形
C.当OA=OB时,四边形ABCD是矩形
D.当∠ABD=∠CBD时,四边形ABCD是矩形
7.如图,每个小正方形的边长为l,在△ABC中,点D为AB的中点,则线段CD的长为(
)
A.
B.
C.
D.
8.如图,在?ABCD中,E为BC边上一点,以AE为边作正方形AEFG,若∠BAE=45°,∠CEF=15°,则∠D的度数是( )
A.55°
B.60°
C.65°
D.70°
9.如图,矩形中,,.点、点分别在边、上,点、在对角线
上.若四边形是菱形,则的长为(
).
A.
B.
C.
D.
10.如图,在平面直角坐标系xOy中,菱形ABCD的顶点A的坐标为(2,0),点B的坐标为(0,1),点C在第一象限,对角线BD与x轴平行.直线y=x+3与x轴、y轴分别交于点E、F,将菱形ABCD沿x轴向左平移m个单位,当点D落在△EOF的内部时(不包括三角形的边),m的取值范围是( )
A.4<m<6
B.4≤m≤6
C.4<m<5
D.4≤m<5
二、填空题(每小题3分,共18分)
11.已知正方形的边长为,其周长为________.
12.如图,在菱形ABCD中,过点C作CEBC交对角线BD
于点
E
,若ECD20
,则ADB____________.
13.如图所示,在四边形ABCD中,对角线AC与BD相交于点O,AD∥BC,∠BAD=∠DCB,若不增加任何字母和辅助线,要使得四边形ABCD是矩形,则还需要增加一个条件____
14.如图,G是△ABC的重心,直线l过A点与BC平行.若直线CG分别与AB,直线l交于点D,E两点,直线BG与AC交于F点,则△AED的面积∶四边形ADGF的面积=_________________.
15.如图,顺次连结四边形ABCD四边的中点E、F、G、H,则四边形EFGH的形状一定是____.
16.如图矩形中,AB=8cm,BC=4cm,是的中点,,则四边形的面积为________cm2.
17.如图,正方形ABCD的边长为8,E为AD上一点.
若BE=10,则CE=__________.
18.点P是菱形ABCD的对角线AC上的一个动点,已知AB=1,∠ADC=120°,
点M,N分别是AB,BC边上的中点,则△MPN的周长最小值是______.
三、解答题(共52分)
19.如图,在矩形ABCD,AD=AE,DF⊥AE于点F.求证:AB=DF.
20.如图,四边形ABCD中,∠B=∠C=90°,E为BC的中点,且AE平分∠BAD.
(1)求证:DE平分∠ADC;
(2)试判断AE和DE的位置关系.
21.如图,在□ABCD中,E、F分别是AD、BC的中点,连接AC、CE、AF.
(1)求证△ABF
≌
△CDE;
(2)若AB=AC,求证四边形AFCE是矩形.
22.如图,矩形纸片ABCD(AD>AB)中,将它折叠,使点A与点C重合,折痕EF交AD于点E,交BC于点F,交AC于点O,连结AF,CE.
(1)求证:四边形AFCE是菱形;
(2)若AE=8,△ABF的面积为9,求AB+BF的值.
23.如图,平面直角坐标中,把矩形OABC沿对角线OB所在的直线折叠,点A落在点D处,OD与BC交于点E.OA、OC的长是关于x的一元二次方程x2﹣9x+18=0的两个根(OA>OC).
(1)求A、C的坐标.
(2)直接写出点E的坐标,并求出过点A、E的直线函数关系式.
(3)点F是x轴上一点,在坐标平面内是否存在点P,使以点O、B、P、F为顶点的四边形为菱形?若存在请直接写出P点坐标;若不存在,请说明理由.
24.如图,现有一张边长为4的正方形纸片ABCD,点P为AD边上的一点,将正方形纸片折叠,使点B落在点P处,点C落在点G处,PG交DC于点H,折痕为EF,连接BP,BH.
(1)求证:∠APB=∠BPH;
(2)当点P在边AD上移动(不与点A、点D重合)时,⊿PDH的周长是否发生变化?请证明你的结论.
参考答案
1.B
2.A
3.D
4.B
5.B
6.D
7.A
8.B
9.D
10.A
11.
12.35°
13.AC=BD或∠BAD=90°(答案不唯一)
14.3:2
15.平行四边形
16.10
17.2
18..
19.∵四边形ABCD是矩形,∴AD∥BC,∠B=90°,∴∠AEB=∠DAE.
∵DF⊥AE,∴∠AFD=∠B=90°.在△ABE和△DFA中,
∵
∴△ABE≌△DFA,∴AB=DF.
点睛:本题考查了全等三角形的判定与性质、矩形的性质的知识,属于基础题,难度不是很大,熟练掌握全等三角形的判定与性质是关键.
20..如图作EF∥AB∥CD,
∵AE平分∠BAD,
∴∠BAE=∠FAE=∠AEF,
∴AF=FE.
又∵点E为BC中点,
∴F为AD中点,
∴AF=FE=FD,
∴∠FDE=∠FED=∠EDC,
∴DE平分∠ADC.
(2)由(1)易知AE与DE垂直.
21.(1)∵
四边形ABCD是平行四边形,∴
AB=CD,AD=BC,∠B=∠D.
∵
E、F分别是AD、BC的中点,
∴
DE=AE=
AD,
BF=CF=
BC.∴
BF=DE,CF=AE.
∴
△ABF≌△CDE(SAS).
(2)∵△ABF≌△CDE(SAS),
∴
AF=CE.
又∵CF=AE,
∴四边形AFCE是平行四边形.
∵AB=AC,
F分别是BC的中点,
∴AF⊥BC.
即∠AFC=90°.
∴四边形AFCE是矩形.
22.
(1)证明:当顶点A与C重合时,折痕EF垂直平分AC,
∴OA=OC,∠AOE=∠COF=90°,
∵在矩形ABCD中,AD∥BC,
∴∠EAO=∠FCO,
∴△AOE≌△COF(ASA),
∴OE=OF,
∴四边形AFCE是平行四边形,
又∵EA=EC
∴平行四边形AFCE是菱形.
(2)∵四边形AFCE是菱形,
∴AF=AE=8,在Rt△ABF中,AB2+BF2=AF2,
∴AB2+BF2=64,∴(AB+BF)2-2AB·BF=64①,
∵△ABF的面积为9,
∴AB·BF=9,
∴AB·BF=18②,
由①、②得:(AB+BF)2=100,
∵AB+BF>0,
∴AB+BF=10.
23.(1)A(6,0),C(0,3);(2)E(,3),y=﹣x+;(3)满足条件的点P坐标为(6﹣3,3)或(6+3,3)或(,3)或(6,﹣3).
(1)由x2﹣9x+18=0可得x=3或6,
∵OA、OC的长是关于x的一元二次方程x2﹣9x+18=0的两个根(OA>OC),
∴OA=6,OC=3,
∴A(6,0),C(0,3).
(2)如图1中,
∵OA∥BC,
∴∠EBC=∠AOB,
根据翻折不变性可知:∠EOB=∠AOB,
∴∠EOB=∠EBO,
∴EO=EB,设EO=EB=x,
在Rt△ECO中,∵EO2=OC2+CE2,
∴x2=32+(6﹣x)2,
解得x=,
∴CE=BC﹣EB=6﹣=,
∴E(,3),
设直线AE的解析式为y=kx+b,则有,
解得,
∴直线AE的函数解析式为y=﹣x+.
(3)如图,OB==3.
①当OB为菱形的边时,OF1=OB=BP1=3=,故P1(6﹣3,3),
OF3=P3F3=BP3=3,故P3(6+3,3).
②当OB为菱形的对角线时,∵直线OB的解析式为y=x,
∴线段OB的垂直平分线的解析式为y=﹣2x+,
可得P2(,3),
③当OF4问问对角线时,可得P4(6,﹣3)
综上所述,满足条件的点P坐标为(6﹣3,3)或(6+3,3)或(,3)或(6,﹣3).
24.
(1)由折叠的性质,得,,
∴,
∴,
即.
∵,
∴,
∴.
(2)的周长不变.证明如下:
过点作,垂足为.
由(1)知.
在和中,
∴,
∴,.
∵,
∴.
在和中,
∴,
∴.
∴的周长为.
故的周长不发生变化.
【点睛】
考查了翻折变换的性质以及全等三角形的判定与性质和勾股定理、二次函数的最值问题等知识,熟练利用全等三角形的判定得出对应相等关系是解题关键.
第4题图
第5题图
第7题图
第8题图
第9题图
第10题图
第12题图
第13题图
第14题图
第15题图
第16题图
第17题图
第18题图
试卷第1页,总3页
试卷第1页,总3页
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
