3.3圆心角(2)

(共8张PPT)
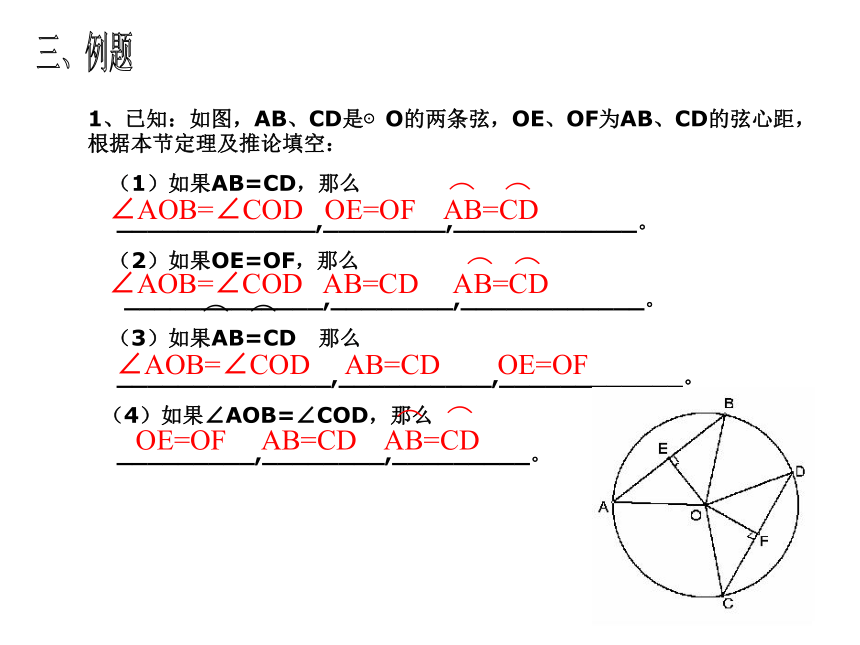
1、已知：如图，AB、CD是⊙O的两条弦，OE、OF为AB、CD的弦心距，根据本节定理及推论填空：
（1）如果AB=CD，那么
_____________,________,____________。
（2）如果OE=OF，那么
_____________,________,____________。
（3）如果AB=CD 那么
______________,__________,____________。
（4）如果∠AOB=∠COD，那么
_________,________,_________。
⌒
⌒
∠AOB=∠COD OE=OF AB=CD
⌒
⌒
∠AOB=∠COD AB=CD AB=CD
⌒
⌒
∠AOB=∠COD AB=CD OE=OF
OE=OF AB=CD AB=CD
⌒
⌒
根据在一个圆中等弧对等弦,小明同学认为:如图
若AB=2CD,则AB=2CD你同意他的说法吗 请说明理
解:取AB中点E,
AB=2CD
AE
EB=CD
AE=BE=CD
E
又∵AE+BE>AB
2CD2AB
明同学的说法不正确
B
E
A
验证逆命题
(3)请结合右图判断以下三个命题是否为真命题
几何语言:
B
如图,∠AOB=∠COD
C
AB=CD
分>OE=OF
AB
CD
(2)请把题设中“圆心角相等”与三个结论中任意一个
的交换写出新命题
条件
结论
在同圆或等圆中
弦心距所对的弧相等
那么弦心距所对的弦相等
如果弦心距相等
弦心距所对的圆心角相等
命题
命题二
命题三
想一想
你能设计出一种方法,使锯出的木材的正方形截面
积大于上述所得的面积吗 小于呢
答:不能.以直径为对角线
的正方形是圆内接四边形中
最大的,小于上述所得的面
积有很多
已知等边三角形ABC的边长为23cm,求它的外接
园半径
解:如图所示,连结OA,OB
OC,并延长AO交BC于点D
AB=BC=AC
∴∠AOB=∠COB=∠AOC=120°,
∠BOD=∠COD=60°
OB=OC
D
OD⊥BC,
∠BAD=30°,BD=√3cm
设OB=r,则OD=r
7)+
r=2cm
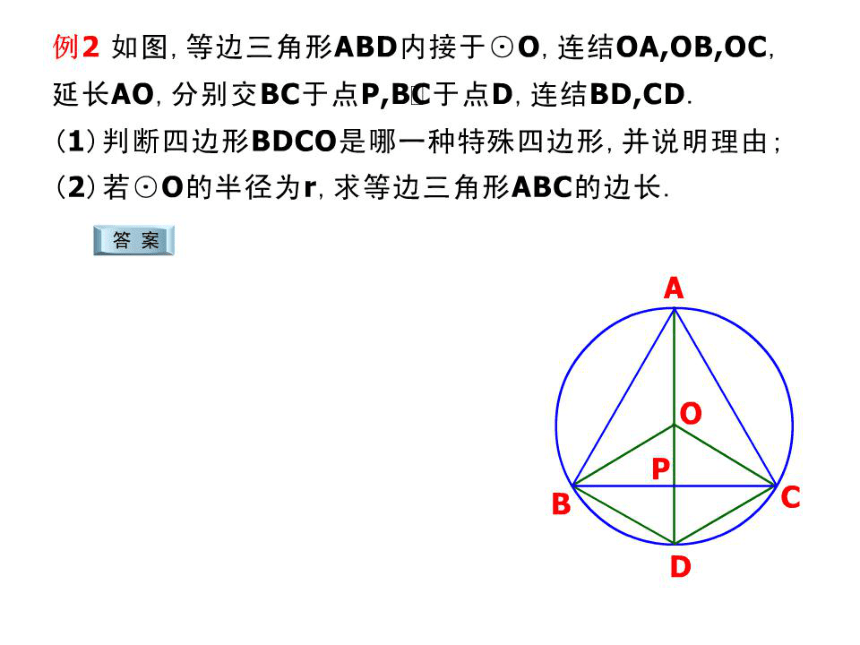
判断四边形BDco是哪一种特殊四边形,并说明理
为r,求等边三角形ABc的边长
(3)若等边△ABC的边长为
求她的外接圆半径(课内练习