基于三角形面积背景下的直线解析式问题

(共12张PPT)
金华四中教育集团 童桂恒
基于三角形面积背景下的直线解析式问题
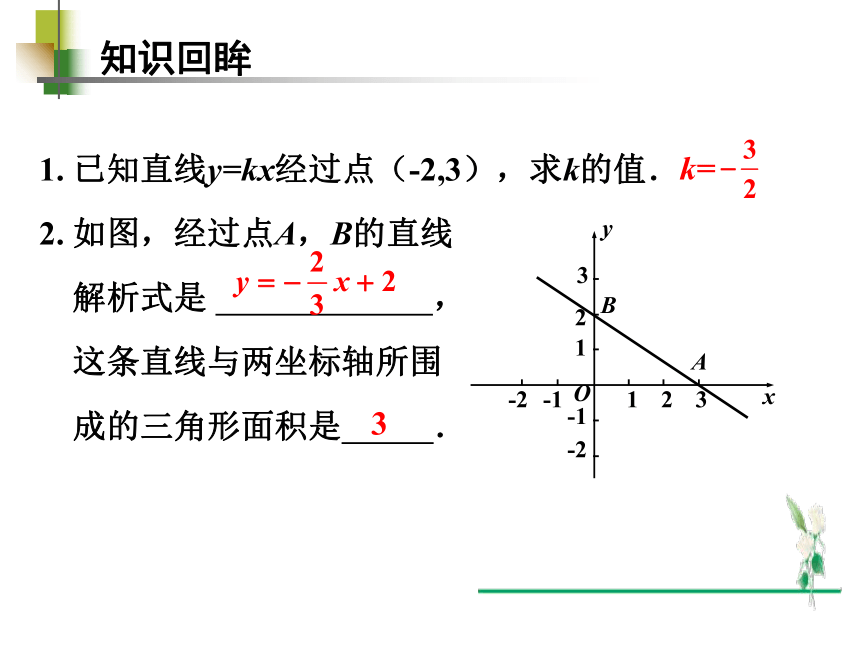
1. 已知直线y=kx经过点（-2,3），求k的值．
2. 如图，经过点A，B的直线
解析式是 ，
这条直线与两坐标轴所围
成的三角形面积是 ．
知识回眸
A
B
O
x
y
1
2
3
-1
-2
3
1
2
-1
-2
k=
3
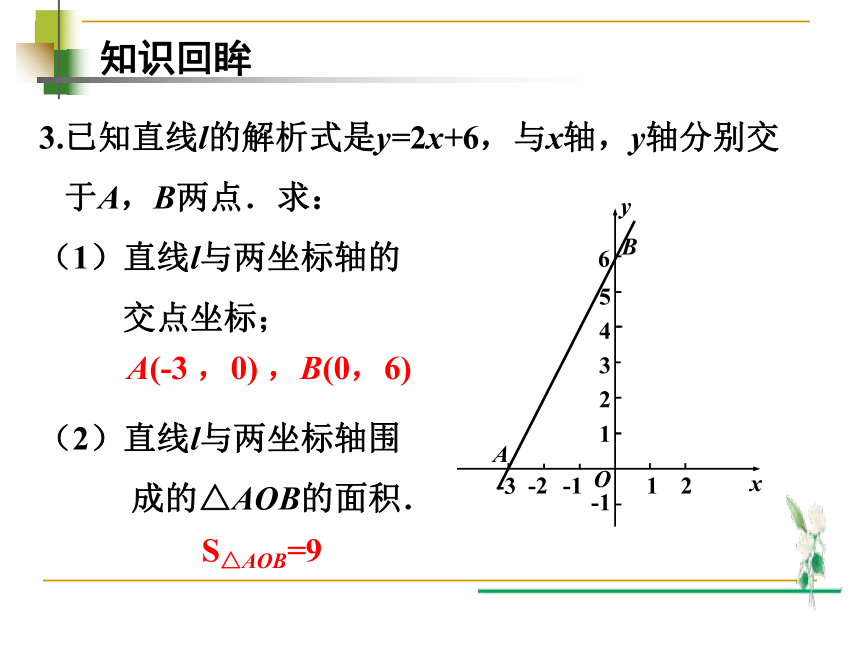
3.已知直线l的解析式是y=2x+6，与x轴，y轴分别交
于A，B两点．求：
（1）直线l与两坐标轴的
交点坐标；
（2）直线l与两坐标轴围
成的△AOB的面积．
知识回眸
B
A
O
x
y
1
2
4
-1
-2
3
1
2
-1
-3
6
5
A(-3 ，0) ，B(0，6)
S△AOB=9
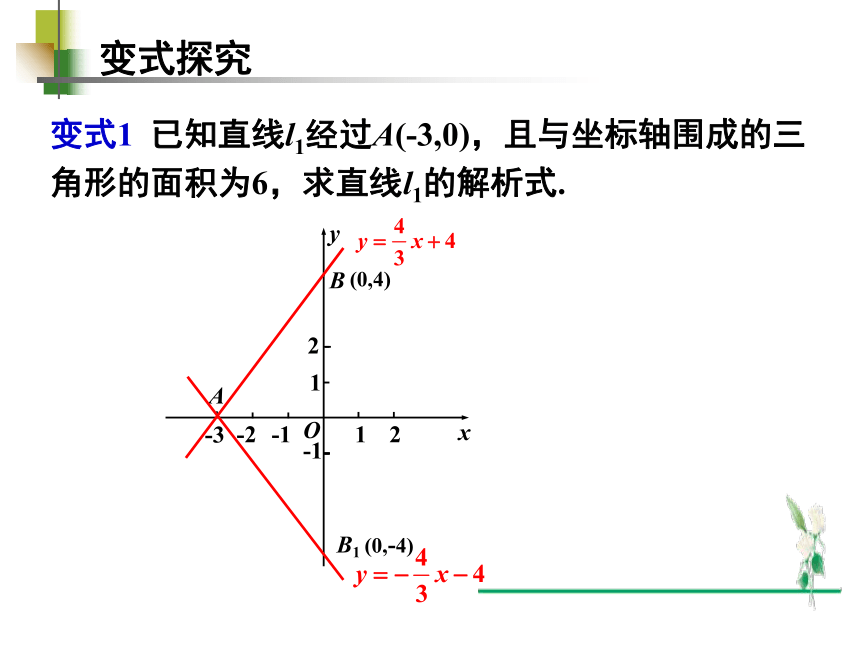
变式1 已知直线l1经过A(-3,0)，且与坐标轴围成的三角形的面积为6，求直线l1的解析式.
变式探究
A
O
x
y
1
2
-1
-2
1
2
-1
-3
B
B1
(0,-4)
(0,4)
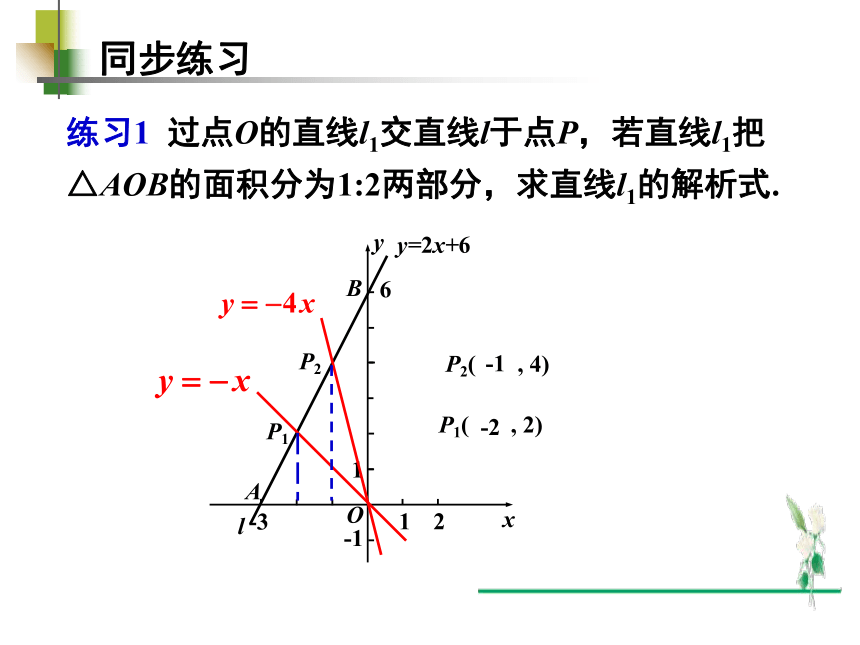
练习1 过点O的直线l1交直线l于点P，若直线l1把
△AOB的面积分为1:2两部分，求直线l1的解析式.
同步练习
B
A
O
x
y
1
2
1
-1
-3
6
l
P1
P2
y=2x+6
P1( , 2)
P2( , 4)
-2
-1
变式2 过点O的直线l2交直线l于点Q，若直线l2，直线l与坐标轴所围成的三角形面积为△AOB的面积的一半，求直线l2的解析式.
变式探究
B
A
O
x
y
1
2
4
-1
-2
3
1
2
-1
-3
6
5
Q1
Q2
Q3
Q3( 1.5 , 9)
Q2 (-1.5 , 3)
( ,-3)
y=2x+6
-4.5
l
同步练习
B
A
O
x
y
1
2
4
-1
-2
3
1
2
-1
-3
6
5
练习2 过点O的直线l2交直线l于点R，若直线l2，直
线l与坐标轴所围成的三角形面积为△AOB的面积的
三分之一，求直线l2的解析式.
R1
R1 (-4,-2)
R3
R4
R2
y=2x+6
R2 (-2, 2)
R3 (-1, 4)
R4 ( 1, 8)
l
1.解决这类问题需要用到哪些数学思想方法？
交流提升
2. 你还有哪些问题需要提出来的？
拓展延伸
变式3 如图，以AO、OB为相邻两边补成一个长方形AOBC，若直线l3过△AOB的顶点，且把长方形AOBC的面积分为1:2两部分，求直线l3的解析式.
当直线l3过点O时:
当直线l3过点B时:
当直线l3过点A时:
D2
D1
D1 (-3,4)
D2 (-2, 6)
E1 (-2,0)
E2 (-3, 2)
E2
E1
F1 (-1,6)
F2 (0, 3)
F2
F1
B
A
O
x
y
1
2
4
-1
-2
3
1
2
-1
-3
6
5
C
顶点
练习3 如图，以AO、AB为邻边补成一个平行四边形AOCB，若直线l3过△AOB的顶点，且把平行四边形AOCB的面积分为1:2两部分，求直线l3的解析式.
同步练习
C
B
A
O
x
y
1
2
4
-1
-2
3
1
2
-1
-3
6
5
当直线l3过点O时:
当直线l3过点B时:
当直线l3过点A时:
D2
D1
D1 (1,6)
D2 (-1, 4)
E1 (1,2)
E2 (-1, 0)
E2
E1
F1 (2,6)
F2 (2, 4)
F2
F1
y=2x+6
链接中考
已知：直线 与x轴，y轴分别交于
点A，B，把线段AB绕点A顺时针方向旋转90°得
线段AC，连接BC．若动点P（a， ）使△ABP面
积与△ABC面积相等，求a的值.
x
y
O
A
B
C