4.2证明（2）

　　4.2证明（2）
班级 _________姓名_________学号_________
学习目标：
１．进一步体会证明的含义；
　２．探索并理解三角形内角和定理的几何证明；
课前预习：
1．三角形的一个外角等于_________的两个内角的和．
2．在△ABC中，若∠A：∠B：∠C=1：2：3，则∠C=________．
3．在△ABC中，∠B=45°，∠C=72°，那么与∠A相邻的一个外角等于_______．
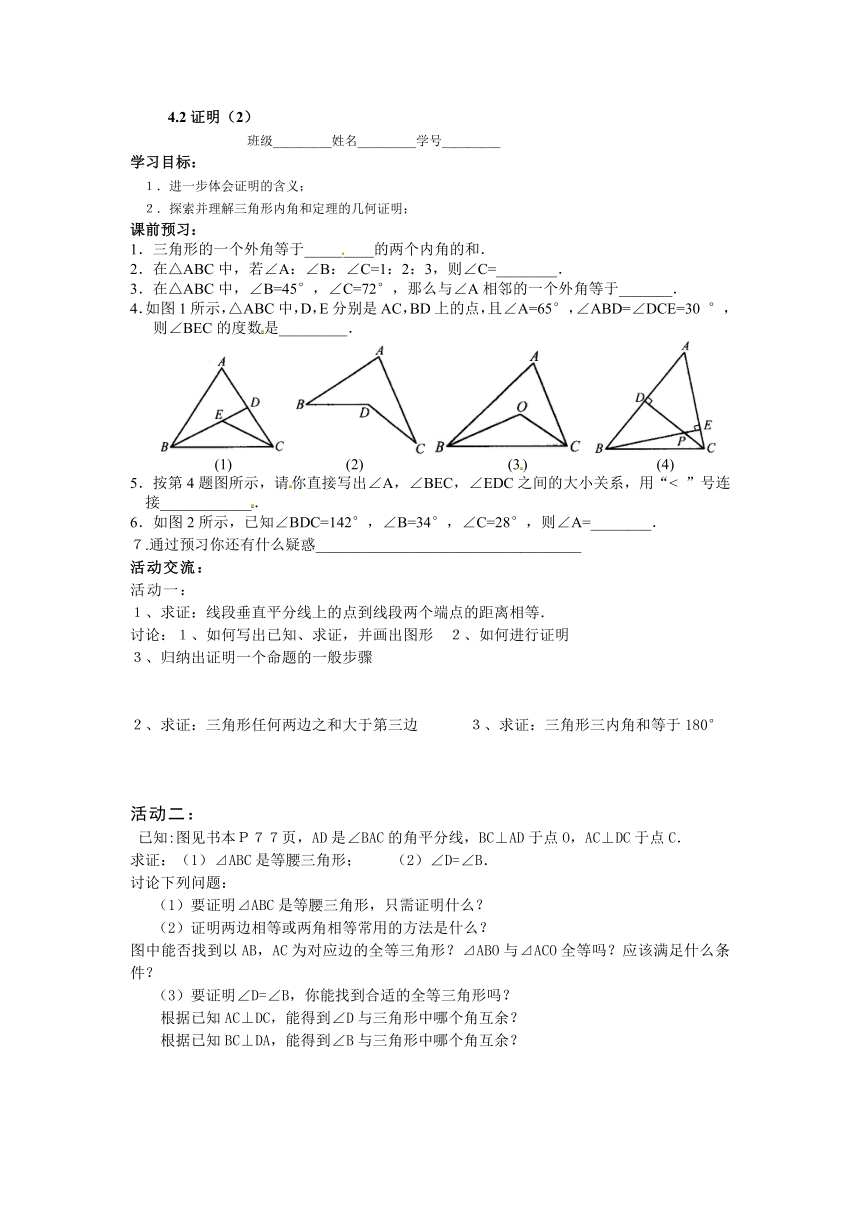
4．如图1所示，△ABC中，D，E分别是AC，BD上的点，且∠A=65°，∠ABD=∠DCE=30°，则∠BEC的度数是_________．
(1) (2) (3) (4)
5．按第4题图所示，请你直接写出∠A，∠BEC，∠EDC之间的大小关系，用“<”号连接____________．
6．如图2所示，已知∠BDC=142°，∠B=34°，∠C=28°，则∠A=________．
７.通过预习你还有什么疑惑___________________________________
活动交流：
活动一：
１、求证：线段垂直平分线上的点到线段两个端点的距离相等．
讨论：１、如何写出已知、求证，并画出图形 ２、如何进行证明
３、归纳出证明一个命题的一般步骤
２、求证：三角形任何两边之和大于第三边 ３、求证：三角形三内角和等于180°
活动二：
已知:图见书本Ｐ７７页，AD是∠BAC的角平分线，BC⊥AD于点O，AC⊥DC于点C．
求证：（1）⊿ABC是等腰三角形；　　（2）∠D=∠B．
讨论下列问题：
（1）要证明⊿ABC是等腰三角形，只需证明什么？
（2）证明两边相等或两角相等常用的方法是什么？
图中能否找到以AB，AC为对应边的全等三角形？⊿ABO与⊿ACO全等吗？应该满足什么条件？
（3）要证明∠D=∠B，你能找到合适的全等三角形吗？
根据已知AC⊥DC，能得到∠D与三角形中哪个角互余？
根据已知BC⊥DA，能得到∠B与三角形中哪个角互余？
当堂检测：
书本Ｐ７８页作业题
课后作业：
１．如果三角形的一个外角小于和它相邻的内角，则这个三角形是（ ）
A．锐角三角形; B．直角三角形; C．钝角三角形; D．都有可能
２．若等腰三角形的一个外角为110°，则它的底角为（ ）
A．55° B．70° C>55°或70° D．以上答案都不对
３．若三角形的三个外角的度数之比为2：3：4，则与之对应的三个内角的度数之比为（ ）
A．4：3：2 B．3：2：4 C．5：3：1 D．3：1：5
４．满足下列条件的△ABC中，不是直角三角形的是（ ）
A．∠B+∠A=∠C B．∠A：∠B：∠C=2：3：5
C．∠A=2∠B=3∠C D．一个外角等于和它相邻的一个内角
５．如图3所示，在△ABC中，∠ABC与∠BAC的平分线相交于点O，若∠BOC=120°，则∠A为（ ）
A．30° B．60° C．80° D．100°
６．如图所示，在锐角△ABC中，CD和BE分别是AB和AC边上的高，且CD和BE交于点P，若∠A=50°，则∠BPC的度数是（ ）
A．150° B．130° C．120° D．100°
７．如图4所示，点B，D，E，C在同一条直线上，且∠1=∠2，BD=EC，
求证：△ABE≌△ACD．
８．如图所示，BC⊥ED，垂足为O，∠A=27°，∠D=20°，求∠ACB与∠B的度数．
15．（提高）如图所示，已知等腰直角三角形ABC中，∠ACB=90°，直线L经过点C，AD⊥L，BE⊥L，垂足分别为D，E．
（1）证明：△ACD≌△CBE；
（2）求证：DE=AD+BE；
（3）当直线L经过△ABC内部时，其他条件不变；（2）中的结论还成立吗？如果成立，请给出证明；如果不成立，这时DE，AD，BE有什么关系？证明你的猜想．
课后反思：