一元二次方程复习课

(共21张PPT)
把我们的家建设的更美丽
一元二次方程小结
每年3月5日， 我校开展学雷锋献爱心活动，全校师生踊跃捐款,据统计三（1）班在2010年捐款1000元，且每年捐款额的增长率相同，到今年已累计达4750元， 你知道三(1)班的同学们在今年3月5日捐了多少吗？
解：
设增长率为x，2010年捐了1000元，
则2011年捐了1000（x+1）元，2012年捐了1000 （x+1）2元
根据题意得：
1000+1000（x+1）+ 1000（x+1）2 = 4750
这个问题可以用我们学过的什么知识来解决？
观察方程
③等号两边都是整式
①只含有一个未知数
②未知数的最高次数是2次
这样的方程叫
一元二次方程
特征如下：
有何特征？
(1) 2x = y 2 - 1
(3) x 2- - 3 = 0
2
x
(4) 3z2+1 = z (2z2 - 1)
(5) x 2 = 0
结论：以上方程中(2)、(5)、(6)是一元二次方程
(6) ( x + 2) 2 = 4
请判断下列方程是否为一元二次方程：
1000+1000（x+1）+ 1000（x+1）2 = 4750
整理得：
X2+3X-1.75 = 0
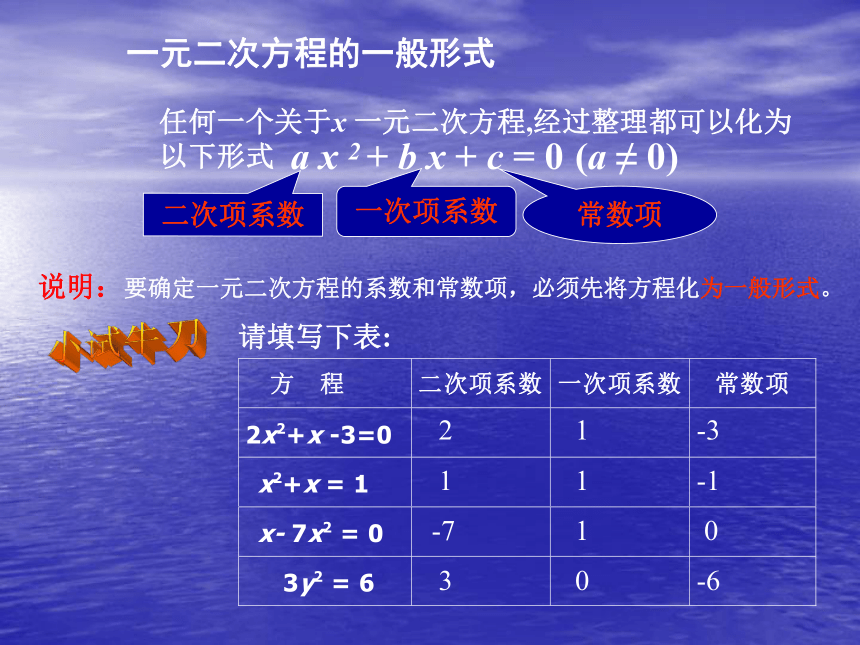
一元二次方程的一般形式
任何一个关于x 一元二次方程,经过整理都可以化为以下形式
a x 2 + b x + c = 0
(a ≠ 0)
二次项系数
一次项系数
常数项
2
1
-3
1
1
-1
-7
1
0
3
0
-6
说明：要确定一元二次方程的系数和常数项，必须先将方程化为一般形式。
请填写下表:
一元二次方程的解法
1.因式分解法。
2.开平方法。
3.配方法。
4.公式法
1.把二次项,一次项移到等号左边,常数项移到等号右边。
2.两边同加上一次项系数一半的平方。
你会解这个方程吗？X2+3X-1.75 = 0
用适当的方法解下列方程
（1）
（2）
（3）
（4）
（配方法）
解：
设增长率为x，2010年捐了1000元，
则2011年捐了1000（x+1）元，2012年捐了1000 （x+1）2元
根据题意得：
1000+1000（x+1）+ 1000（x+1）2 = 4750
X2+3X-1.75 = 0
解得x=0.5 x=-3.5(不符合题意,舍去)
所以该班今年捐款1000(1+0.5)2=2250元
每年3月5日， 我校开展学雷锋献爱心活动，全校师生踊跃捐款,据统计三（1）班在2010年捐款1000元，且每年捐款额的增长率相同，到今年已累计达4750元， 你知道三(1)班的同学们在今年3月5日捐了多少吗？
学校决定在实验楼后一块长32米,宽20米的长方形空地上,计划修筑若干条笔直等宽道路，余下部分作花坛，请你在这块空地上设计一个方案, 要求花坛面积为540m2，并求出方案中道路的宽为多少米？
20
32
某希望小学准备用部分资金买一批课外阅读书给学生们阅读，原价每本30元，书店老板给他们提供了优惠方案：买300本全部打8折，若多买100本，则每本又可降价1元，但最低不得低于16元，那么用相同的资金可买
分析：利用“图形经过平移”，它的面积大小不会改变的道理，把纵横两条路平移一下
答：道路宽为2米。
32
20
解：设道路的宽为 米，根据题意得，
化简，得
解得 1＝2， 2＝50
要求花坛面积为540平方米，并求出方案中道路的宽为多少米？
经检验， 不符合题意，舍去。
32
20
答：道路宽为1米。
解：设道路宽为x 米,则花坛的长为
解得
X
X
X
X
(32-2x)米，宽为（20-2x) 米，根据题意得：
要求花坛面积为540平方米，并求出方案中道路的宽为多少米？
经检验， 不符合题意，舍去。
学校决定在花坛中种植玫瑰，经调查发现，如果商家每株玫瑰要盈利10元，平均每天可售出40株.为扩大销售，若每株降价1元，则平均每天可多售出8株. 如果商家每天要盈利432元，同时也让顾客获得最大 的实惠.那么每株玫瑰应降价多少元？
盈利
… … …
每束利润 × 束数 = 利润
每株利润
株数
10
40
利润
10×40
降价1元
10﹣1
40﹢8×1
降价2元
10﹣2
40﹢8×2
降价X元
10﹣X
40﹢8X
432
解：设每株玫瑰应降价X元，则每株获利
（10-X）元，平均每天可售出（40+8X）株，
（10-X）（40+8X）= 432
整理得：
X2-5X+4=0
解得：
X1=1 X2=4
经检验：X2=4 符合题意
数量关系
（ ）×（ ）
每株利润
株数
利润
=
由题意得：
10-X
40+8X
432
商家每天要盈利432元，
那么每株玫瑰应降价4元。
答:
问题: 从2010年初到现在,木材的价格提高了44% ,若每一年比前一年提高的这个百分比相同,求这个百分数
解：设这个百分数为X，根据题意得：
解得：
学校要建一个长方形的实验基地，基地的一边靠墙,墙长２0米，另三边用长40米的木栏围成。到木材店买木材,老板说只要我们能帮他解决一个问题,他就给我们打个折。
答：这个百分比为20%
经检验， 不符合题意，舍去。
长方形的实验基地，基地的一边靠墙，墙长２0米，另三边用长度为40米的木栏围成。
（1）要使基地的面积达到150平方米，则这个长方形基地的两边长分别为多少？
X
X
40-2X
解：设长方形的一边为X米，则另一边为（40-2X）米，根据题意得：
解得：
答：长方形基地的两边分别为15米，10米。
经检验X1=5舍去　　　X2=15符合题意
∴40-2X=30或１０
长方形的实验基地，基地的一边靠墙，墙长２0米，另三边用长度为40m的木栏围成。
（2）基地的面积能达到250平方米吗？为什么？（通过计算说明）
X
X
40-2X
解：设长方形的一边为X米，则另一边为（40-2X）米，根据题意得：
化简得：
所以方程无实数根,即长方形基地的面积不能达到250。
长方形的实验基地，基地的一边靠墙，墙长２0米，另三边用长为40m的木栏围成。
（3）基地的面积最大能达到多少平方米？
X
X
40-2X
解：设长方形的一边为X米，则另一边为（40-2X）米，根据题意得：
原式=
所以当X=10米时，长方形的最大面积为200平方米。
？
小结：
这节课你有哪些收获？
作业：作业本（一）复习题
1.关于y的一元二次方程2y(y-3)= -4的一般形式是_________ ,它的二次项系数是_____,一次项是_____,
2.已知方程 的一个根是- 1，则k= , 另一根为______
2y2-6y+4=0
2
-6y
4
x=-3