2020-2021学年浙江省八年级下学期期末复习数学专题训练——专题2一元二次方程(word解析版)
文档属性
| 名称 | 2020-2021学年浙江省八年级下学期期末复习数学专题训练——专题2一元二次方程(word解析版) |  | |
| 格式 | docx | ||
| 文件大小 | 77.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-02 14:04:04 | ||
图片预览




文档简介
2021年浙江八年级数学期末考试专题训练——专题2一元二次方程
一.选择题(共10小题)
1.(2021春?余姚市校级期中)关于x的一元二次方程(a﹣1)x2﹣2x﹣1=0有两个实数根,则实数a的取值范围是( )
A.a≥0
B.a≥0且a≠1
C.a>0
D.a>0且a≠1
2.(2021春?鹿城区校级期中)用配方法解一元二次方程x2﹣6x+3=0化成(x+a)2=b的形式,则a、b的值分别是( )
A.3,12
B.﹣3,12
C.3,6
D.﹣3,6
3.(2021春?余杭区期中)把方程x2﹣4x﹣1=0转化成(x+m)2=n的形式,则m,n的值是( )
A.2,3
B.2,5
C.﹣2,3
D.﹣2,5
4.(2021春?下城区期中)对于一元二次方程ax2+bx+c=0(a≠0),下列说法:
①若a+b+c=0,则b2﹣4ac≥0;
②若方程ax2+c=0有两个不相等的实根,则方程ax2+bx+c=0必有两个不相等的实根;
③若c是方程ax2+bx+c=0的一个很,则一定有ac+b+1=0成立;
④若x0是一元二次方程ax2+bx+c=0的根,则b2﹣4ac=(2ax0+b)2.
其中正确的( )
A.①②④
B.①②③
C.①③④
D.②③④
5.(2021春?长兴县月考)关于x的一元二次方程nx2x+2=0有两个不相等的实数根,则n的取值范围是( )
A.n且n≠0
B.n
C.n且n≠0
D.n且n≠0
6.(2021春?上城区校级期中)用配方法解一元二次方程x2+2x﹣3=0,配方后得到的方程是( )
A.(x﹣1)2=4
B.(x+1)2=4
C.(x+2)2=1
D.(x﹣2)2=1
7.(2020?播州区校级模拟)已知一元二次方程ax2+bx+c=0(a≠0)中,下列说法:
①若a+b+c=0,则b2﹣4ac>0;
②若方程两根为﹣1和2,则2a+c=0;
③若方程ax2+c=0有两个不相等的实根,则方程ax2+bx+c=0必有两个不相等的实根;
④若b=2a+c,则方程有两个不相等的实根.其中正确的有( )
A.①②③
B.①②④
C.②③④
D.①②③④
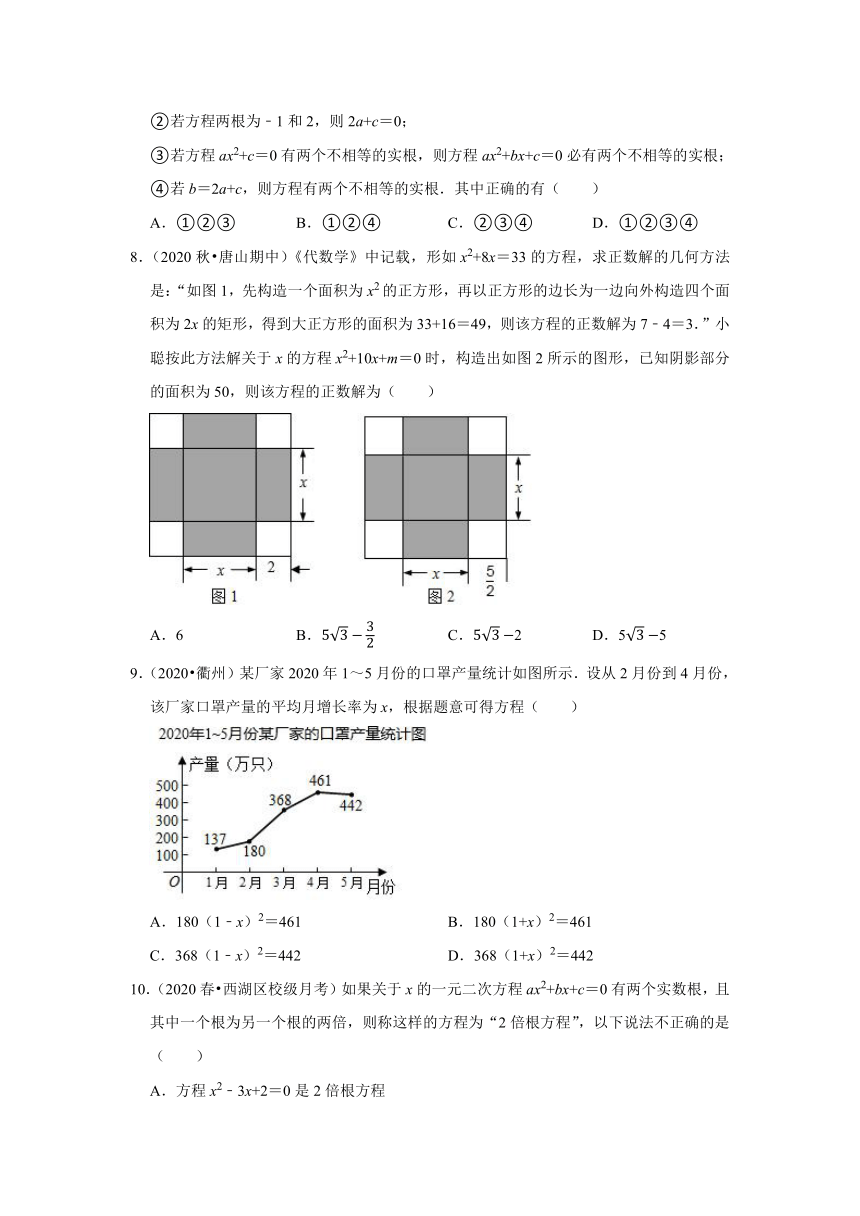
8.(2020秋?唐山期中)《代数学》中记载,形如x2+8x=33的方程,求正数解的几何方法是:“如图1,先构造一个面积为x2的正方形,再以正方形的边长为一边向外构造四个面积为2x的矩形,得到大正方形的面积为33+16=49,则该方程的正数解为7﹣4=3.”小聪按此方法解关于x的方程x2+10x+m=0时,构造出如图2所示的图形,已知阴影部分的面积为50,则该方程的正数解为( )
A.6
B.
C.2
D.55
9.(2020?衢州)某厂家2020年1~5月份的口罩产量统计如图所示.设从2月份到4月份,该厂家口罩产量的平均月增长率为x,根据题意可得方程( )
A.180(1﹣x)2=461
B.180(1+x)2=461
C.368(1﹣x)2=442
D.368(1+x)2=442
10.(2020春?西湖区校级月考)如果关于x的一元二次方程ax2+bx+c=0有两个实数根,且其中一个根为另一个根的两倍,则称这样的方程为“2倍根方程”,以下说法不正确的是( )
A.方程x2﹣3x+2=0是2倍根方程
B.若关于x的方程(x﹣2)(mx+n)=0是2倍根方程,则m+n=0
C.若m+n=0且m≠0,则关于x的方程(x﹣2)(mx+n)=0是2倍根方程
D.若2m+n=0且m≠0,则关于x的方程x2+(m﹣n)x﹣mn=0
是2倍根方程
二.填空题(共4小题)
11.(2021春?下城区期中)将x2﹣2x﹣2=0配方成(x+m)2=n的形式,则n=
.
12.(2021?海淀区校级模拟)如图,某小区规划在一个长30m、宽20m的长方形ABCD土地上修建三条同样宽的通道,使其中两条与AB平行,另一条与AD平行,其余部分种花草.要使每一块花草的面积都为78m2,那么通道的宽应设计成多少m?设通道的宽为xm,由题意列得方程
.
13.(2021春?余杭区期中)已知三角形两边的长分别是4和3,第三边的长是一元二次方程x2﹣8x+15=0的一个实数根,则该三角形的面积是
.
14.(2020?山西模拟)准备在一块长为30米,宽为24米的长方形花圃内修建四条宽度相等,且与各边垂直的小路,(如图所示)四条小路围成的中间部分恰好是一个正方形,且边长是小路宽度的4倍,若四条小路所占面积为80平方米,则小路的宽度为
米.
三.解答题(共16小题)
15.(2021春?余姚市校级期中)解方程:
(1)x2﹣6x=0;
(2)x2﹣2x=2x+1.
16.(2021春?拱墅区校级期中)解下列方程:
(1)x2﹣4x﹣1=0;
(2)3x2=8x.
17.(2021春?下城区期中)已知关于x的一元二次方程:x2﹣(2k+1)x+4(k)=0.
(1)求证:这个方程总有两个实数根;
(2)若等腰△ABC的一边长a=4,另两边长b、c,恰好是这个方程的两个实数根,求△ABC的周长.
(3)若方程的两个实数根之差等于3,求k的值.
18.(2021春?鹿城区校级期中)(1)计算:;
(2)解方程:x2﹣4x=5.
19.(2021春?余杭区期中)端年节吃粽子是中国古老的传统习俗,某粽子批发店卖出每个粽子的利润为2元,根据员工情况,每天最多能做1100个,由市场调查得知,若每个粽子的单价降低x元,则粽子每天的销售量y(个)关于x(元)的函数关系式为y=800x+400.
(1)若每个粽子降价0.2元,则该店每天的销售量为
个,每天的总利润为
元.
(2)当每个粽子的单价降低多少元时,该店每天的总利润刚好是1200元?
20.(2021春?拱墅区校级期中)解方程:
(1)7x(5x+2)=6(5x+2);
(2)x2﹣1.
21.(2021春?上城区校级期中)如图,利用一面墙(墙长25米),用总长度49米的栅栏(图中实线部分)围成一个矩形围栏ABCD,且中间共留两个1米的小门,设栅栏BC长为x米.
(1)AB=
米(用含x的代数式表示);
(2)若矩形围栏ABCD面积为210平方米,求栅栏BC的长;
(3)矩形围栏ABCD面积是否有可能达到240平方米?若有可能,求出相应x的值;若不可能,则说明理由.
22.(2021春?柯桥区月考)解方程:
(1)x2﹣6x﹣9=0;
(2)9(2x+3)2=16(1﹣3x)2.
23.(2020秋?鄄城县期末)用适当的方法求解下列方程:
(1)x2﹣2x﹣1=0;
(2)(x+4)2=5(x+4).
24.(2019秋?江北区校级期末)象山红美人柑橘是我省农科院研制的优质品种,宁波市某种植基地2017年种植“象山红美人”100亩,到2019年“象山红美人”的种植面积达到196亩.
(1)求该基地这两年“象山红美人”种植面积的平均增长率.
(2)市场调查发现,当“象山红美人”的售价为45元/千克时,每天能售出200千克,售价每降价1元,每天可多售出50千克,为了推广宣传,基地决定降价促销,同时减少库存,已知该基地“象山红美人”的平均成本价为33元/千克,若使销售“象山红美人”每天获利3150元,则售价应降低多少元?
25.(2020春?温州期末)疫情期间,某公司向厂家订购A,B两款洗手液共50箱.已知购买A款洗手液1箱进价为200元,在此基础上,所购买的A款洗手液数量每增加1箱,每箱进价降低2元.厂家为保障盈利,每次最多可订购30箱A款洗手液.B款洗手液的进价为每箱100元,设该公司购买A款洗手液x箱.
(1)根据信息填表:
型号
数量(箱)
进价(元/箱)
A
x
B
100
(2)若订购这批洗手液的总进价为6240元,则该公司订购了多少箱A款洗手液?
26.(2020春?湖州月考)若m是方程x2﹣2x﹣15=0的一个根,求代数式的值.
27.(2020春?越城区校级月考)如图,在△ABC中,∠B=90°,AB=12cm,BC=16cm.点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动,如果P、Q分别从A、B同时出发,当一个点到达终点时,另一个点也随之停止运动.设运动的时间为t秒.
(1)当t为何值时,△PBQ的面积等于35cm2?
(2)当t为何值时,PQ的长度等于8cm?
(3)若点P,Q的速度保持不变,点P在到达点B后返回点A,点Q在到达点C后返回点B,一个点停止,另一个点也随之停止.问:当t为何值时,△PBQ的面积等于32cm2?
28.(2020春?越城区校级期中)国商大厦某专柜销售一批名牌衬衫,平均每天可销售20件,每件盈利44元为了扩大销售,增加盈利,尽快减少库存,该专柜决定采取适当降价措施.经调查发现,如果每件衬衫每降价1元,专柜平均每天可多售出5件.求该专柜平均每天盈利1600元,且让顾客得到实惠,每件衬衫应降价多少元?
29.(2020秋?鹿城区校级月考)如图是小芳家2019年全年月用电量的条形统计图.据图中提供的信息,解答下列问题:
(1)2019年四个季度中小芳家用电量最大的是第
季度.
(2)求2019年5月至6月用电量的月增长率.
(3)今年(2020年)小芳家添置了新电器.已知今年5月份的用电量是120千瓦时,根据2019年5月至7月用电量的增长趋势,预计今年7月份的用电量将达到240千瓦时,假设今年5月至6月用电量月增长率是6月至7月用电量月增长率的1.5倍,据以上信息可求得小芳家今年6月份的用电量是
千瓦时(直接给出答案).
30.(2020春?上虞区期末)解答下列各题:
(1)用配方法解方程:x2﹣8x﹣4=0.
(2)已知一元二次方程2x2﹣mx﹣m=0的一个根是,求m的值和方程的另一个根.
2021年浙江八年级数学期末考试专题训练——专题2一元二次方程
参考答案与试题解析
一.选择题(共10小题)
1.【解答】解:∵关于x的一元二次方程(a﹣1)x2﹣2x﹣1=0有两个实数根,
∴△=(﹣2)2﹣4×(a﹣1)×(﹣1)=4a≥0,
解得a≥0,
又∵a﹣1≠0,
∴a≥0且a≠1,
故选:B.
2.【解答】解:∵x2﹣6x+3=0,
∴x2﹣6x=﹣3,
则x2﹣6x+9=﹣3+9,即(x﹣3)2=6,
∴x=﹣3,b=6,
故选:D.
3.【解答】解:∵x2﹣4x﹣1=0,
∴x2﹣4x=1,
则x2﹣4x+4=1+4,即(x﹣2)2=5,
∴m=﹣2,n=5,
故选:D.
4.【解答】解:①若a+b+c=0,则x=1是方程ax2+bx+c=0的解,
由一元二次方程的实数根与判别式的关系可知:△=b2﹣4a≥0,故①正确;
②方程ax2+c=0有两个不相等的实根,
∴△=0﹣4ac>0,
∴﹣4ac>0
则方程ax2+bx+c=0的判别式△=b2﹣4a>0,
∴方程ax2+bx+c=0必有两个不相等的实根,故②正确;
③∵c是方程ax2+bx+c=0的一个根,
则ac2+bc+c=0,
∴c(ac+b+1)=0,
若c=0,等式仍然成立,
但ac+b+1=0不一定成立,故③不正确;
④若x0是一元二次方程ax2+bx+c=0的根,
则由求根公式可得:x0,
∴2ax0+b,
∴b2﹣4ac=(2ax0+b)2,故④正确.
故正确的有①②④,
故选:A.
5.【解答】解:∵关于x的一元二次方程nx2x+2=0有两个不相等的实数根,
∴△=()2﹣4n×2>0且n≠0,4n+3≥0,
解得n且n≠0,
故选:C.
6.【解答】解:∵x2+2x﹣3=0,
∴x2+2x=3,
则x2+2x+1=3+1,即(x+1)2=4,
故选:B.
7.【解答】解:①若a+b+c=0,那么x=1为一个实数根.
如果原方程另一个实数根也是1,那么b2﹣4ac=0,
因此①错误;
②把x=﹣1代入方程得到:a﹣b+c=0
(1)
把x=2代入方程得到:4a+2b+c=0
(2)
把(2)式加(1)式×2得到:6a+3c=0,
即:2a+c=0,故正确;
③方程ax2+c=0有两个不相等的实数根,
则它的△=﹣4ac>0,
∴b2﹣4ac>0而方程ax2+bx+c=0的△=b2﹣4ac>0,
∴必有两个不相等的实数根.故正确;
④若b=2a+c则△=b2﹣4ac=(2a+c)2﹣4ac=4a2+c2,
∵a≠0,
∴4a2+c2>0故正确.
②③④都正确,
故选:C.
8.【解答】解:如图2,先构造一个面积为x2的正方形,再以正方形的边长为一边向外构造四个面积为x的矩形,得到大正方形的面积为:
504=50+25=75,
∴该方程的正数解为2=55.
故选:D.
9.【解答】解:从2月份到4月份,该厂家口罩产量的平均月增长率为x,根据题意可得方程:180(1+x)2=461,
故选:B.
10.【解答】解:A、解方程x2﹣3x+2=0得x1=1,x2=2,所以A选项的说法正确,不符合题意;
B、解方程得x1=2,x2,当2×2,则4m+n=0;当2,则m+n=0,所以B选项的说法错误,符合题意;
C、解方程得x1=2,x2,而m+n=0,则x2=1,所以C选项的说法正确,不符合题意;
D、解方程得x1=﹣m,x2=n,而2m+n=0,即n=﹣2m,所以x2=2x1,所以D选项的说法正确,不符合题意.
故选:B.
二.填空题(共4小题)
11.【解答】解:x2﹣2x=2,
x2﹣2x+1=3,
(x﹣1)2=3.
∴n=3.
故答案为:3.
12.【解答】解:由题意可得,
(30﹣2x)(20﹣x)=78×6,
化简,得
x2﹣35x+66=0,
故答案为:x2﹣35x+66=0.
13.【解答】解:解方程x2﹣8x+15=0,得x1=3,x2=5.
当x1=3时,与另两边组成等腰三角形,可求得底边4上的高为,所以该三角形的面积是42=2;
当x2=5时,与另两边组成直角三角形,该三角形的面积=3×4÷2=6.
14.【解答】解:设小路的宽度为x米,则小正方形的边长为4x米,
依题意得:(30+4x+24+4x)x=80
整理得:4x2+27x﹣40=0
解得x1=﹣8(舍去),x2.
故答案为:.
三.解答题(共16小题)
15.【解答】解:(1)x2﹣6x=0,
x(x﹣6)=0,
x=0或x﹣6=0,
解得:x1=0,x2=6;
(2)x2﹣2x=2x+1,
x2﹣4x﹣1=0,
∵b2﹣4ac=(﹣4)2﹣4×1×(﹣1)=16+4=20>0,
∴x,
解得:x1=2,x2=2.
16.【解答】解:(1)x2﹣4x﹣1=0,
∵b2﹣4ac=(﹣4)2﹣4×1×(﹣1)=16+4=20>0,
∴x,
解得:x1=2,x2=2;
(2)3x2=8x,
3x2﹣8x=0,
x(3x﹣8)=0,
x=0或3x﹣8=0,
解得:x1=0,x2;
17.【解答】解:(1)△=(2k+1)2﹣4×1×4(k)
=4k2﹣12k+9
=(2k﹣3)2,
∵无论k取何值,(2k﹣3)2≥0,
故这个方程总有两个实数根;
(2)由求根公式得x,
∴x1=2k﹣1,x2=2.
∵另两边长b、c,恰好是这个方程的两个实数根,
设b=2k﹣1,c=2,
当a,b为腰时,则a=b=4,即2k﹣1=4,计算得出k,
此时三角形周长为4+4+2=10;
当b,c为腰时,b=c=2,此时b+c=a,构不成三角形,
故此种情况不存在.
综上所述,△ABC周长为10.
(3)∵方程的两个实数根之差等于3,
∴,
解得:k=0或3.
18.【解答】解:(1)原式=22;
(2)∵x2﹣4x=5,
∴x2﹣4x﹣5=0,
则(x﹣5)(x+1)=0,
∴x﹣5=0或x+1=0,
解得x1=5,x2=﹣1.
19.【解答】解:(1)由题意可得:若每个粽子降价0.2元,则该店每天的销售量为800×0.2+400=560(个),
每天的总利润为:560×(2﹣0.2)=1008(元).
故答案是:560;1008;
(2)由题意,得(2﹣x)(800x+400)=1200,
解得:x=0.5或x=1.
当x=1时,y=800+400=1200>1100,超过每天可以制作的最大量,故不符合题意.
所以,当每个粽子的单价降低0.5元时,该店每天的总利润刚好是1200元.
20.【解答】解:(1)∵7x(5x+2)=6(5x+2),
∴(5x+2)(7x﹣6)=0,
则5x+2=0或7x﹣6=0,
解得x1,x2;
(2)∵(x﹣1)=(x+1)(x﹣1),
∴(x﹣1)(x﹣1)=0,
则x﹣1=0或x﹣1=0,
解得x1=1,x2.
21.【解答】解:(1)设篱笆BC长为x米,
∵篱笆的全长为49米,且中间共留两个1米的小门,
∴AB=49+2﹣3x=51﹣3x(米),
故答案为:(51﹣3x);
(2)依题意,得:(51﹣3x)x=210,
整理,得:x2﹣17x+70=0,
解得:x1=7,x2=10.
当x=7时,AB=51﹣3x=30>25,不合题意,舍去,
当x=10时,AB=51﹣3x=21,符合题意,
答:篱笆BC的长为10米;
(3)不可能,理由如下:
依题意,得:(51﹣3x)x=240,
整理得:x2﹣17x+80=0,
∵△=(﹣17)2﹣4×1×80=﹣31<0,
∴方程没有实数根,
∴矩形鸡舍ABCD面积不可能达到240平方米.
22.【解答】解:(1)∵x2﹣6x﹣9=0,
∴x2﹣6x=9,
则x2﹣6x+9=9+9,即(x﹣3)2=18,
∴x﹣3,
∴x1=3+3,x2=3﹣3;
(2)∵9(2x+3)2=16(1﹣3x)2,
∴3(2x+3)=4(1﹣3x)或3(2x+3)=﹣4(1﹣3x),
解得x1,x2.
23.【解答】解:(1)∵x2﹣2x﹣1=0,
∴x2﹣2x=1,
则x2﹣2x+1=1+1,即(x﹣1)2=2,
∴x﹣1=±,
∴,;
(2)∵(x+4)2=5(x+4),
∴(x+4)2﹣5(x+4)=0,
则(x+4)(x﹣1)=0,
∴x+4=0或x﹣1=0,
解得x1=﹣4,x2=1.
24.【解答】(1)设该基地这两年种植面积的平均增长率为x,
根据题意可得100(1+x)2=196,
解得x=0.4或﹣2.4(舍去),
答:平均增长率为40%.
(2)设售价应降低m元,
则每天的销量为(200+50m)千克.
根据题意可得(45﹣m﹣33)(200+50m)=3150
解得m=3或5.
答:售价应降低3元或5元.
25.【解答】解:(1)根据题意知,购买B款洗手液的数量是(50﹣x)箱,购买A款洗手液的进价为200﹣2(x﹣1)=(202﹣2x)元.
故答案是:50﹣x;202﹣2x;
(2)设该公司购买A款洗手液x箱,
根据题意知,(202﹣2x)x+100(50﹣x)=6240,
解得x1=31,x2=20.
∵最多可订购30箱A款洗手液,
∴x=20符合题意.
答:该公司购买A款洗手液20箱.
26.【解答】解:∵x2﹣2x﹣15=0,
∴(x﹣5)(x+3)=0.
∴x=5或x=﹣3.
由于m是方程的一个根,所以m=5或﹣3.
∵
2
2
=﹣2(3+m)﹣2
=﹣6﹣2m﹣2.
当m=5时,原代数式无意义;
当m=﹣3时,原式=﹣6﹣2×(﹣3)﹣2
=0﹣2
=﹣2.
27.【解答】解:根据题意知BP=AB﹣AP=12﹣t,BQ=2t.
(1)根据三角形的面积公式,得
PB?BQ=35,
t(12﹣t)=35,
t2﹣12t+35=0,
解得t1=5,t2=7.
故当t为5或7时,△PBQ的面积等于35cm2.
(2)设t秒后,PQ的长度等于8cm,根据勾股定理,得
PQ2=BP2+BQ2=(12﹣t)2+(2t)2=128,
5t2﹣24t+16=0,
解得t1,t2=4.
故当t为或4时,PQ的长度等于8cm.
(3)当0<t≤8时,
PB?BQ=32,即2t×(12﹣t)=32,
则t2﹣12t+32=0,
解得t1=4,t2=8.
当8<t≤12时,
则CQ=2t﹣16,BQ=BC﹣CQ=16﹣(2t﹣16)=32﹣2t,PB=12﹣t,
则△PBQ的面积PB?BQ(12﹣t)×(32﹣2t)=32,
解得:t=20或8(均舍去);
当12<t≤16时,
PB?BQ=32,
(16﹣t)(t﹣12)=32,
t2﹣28t+224=0,
△=282﹣4×1×224=﹣112<0,
故方程无实数根.
综上所述,当t为4或8时,△PBQ的面积等于32cm2.
28.【解答】解:设每件衬衫应降价x元,
根据题意,得
(44﹣x)(20+5x)=1600,
解得:x1=36,x2=4,
∵要尽快减少库存,
∴x=36,
答:每件衬衫应降价36元.
29.【解答】解:(1)①由小芳家2019年全年月用电量的条形统计图得:2019年四个季度中小芳家用电量最大的是第三季度.
故答案为:三;
(2)100%=65%,
答:2019年5月至6月用电量的月增长率为65%;
(3)设今年5月至6月用电量月增长率为1.5x,则6月至7月用电量月增长率的x,
根据题意列方程得:120(1+x)(1+1.5x)=240,
化简得3x2+5x﹣2=0,解得x1,x2=﹣2(不合题意舍去),
∴120×(1+1.5x)=120×(1+1.5)=180(千瓦时),
答:预计小芳家今年6月份的用电量是180千瓦时.
故答案为:180.
30.【解答】解:(1)x2﹣8x﹣4=0,
x2﹣8x=4,
x2﹣8x+16=4+16,
(x﹣4)2=20,
x﹣4,
x1=4+2,x2=4﹣2;
(2)设方程的另一个根是a,
∵一元二次方程2x2﹣mx﹣m=0的一个根是,
∴根据根与系数的关系得:a+(),a,
解得:m=1,a=1,
即m=1,方程的另一个根是1.
一.选择题(共10小题)
1.(2021春?余姚市校级期中)关于x的一元二次方程(a﹣1)x2﹣2x﹣1=0有两个实数根,则实数a的取值范围是( )
A.a≥0
B.a≥0且a≠1
C.a>0
D.a>0且a≠1
2.(2021春?鹿城区校级期中)用配方法解一元二次方程x2﹣6x+3=0化成(x+a)2=b的形式,则a、b的值分别是( )
A.3,12
B.﹣3,12
C.3,6
D.﹣3,6
3.(2021春?余杭区期中)把方程x2﹣4x﹣1=0转化成(x+m)2=n的形式,则m,n的值是( )
A.2,3
B.2,5
C.﹣2,3
D.﹣2,5
4.(2021春?下城区期中)对于一元二次方程ax2+bx+c=0(a≠0),下列说法:
①若a+b+c=0,则b2﹣4ac≥0;
②若方程ax2+c=0有两个不相等的实根,则方程ax2+bx+c=0必有两个不相等的实根;
③若c是方程ax2+bx+c=0的一个很,则一定有ac+b+1=0成立;
④若x0是一元二次方程ax2+bx+c=0的根,则b2﹣4ac=(2ax0+b)2.
其中正确的( )
A.①②④
B.①②③
C.①③④
D.②③④
5.(2021春?长兴县月考)关于x的一元二次方程nx2x+2=0有两个不相等的实数根,则n的取值范围是( )
A.n且n≠0
B.n
C.n且n≠0
D.n且n≠0
6.(2021春?上城区校级期中)用配方法解一元二次方程x2+2x﹣3=0,配方后得到的方程是( )
A.(x﹣1)2=4
B.(x+1)2=4
C.(x+2)2=1
D.(x﹣2)2=1
7.(2020?播州区校级模拟)已知一元二次方程ax2+bx+c=0(a≠0)中,下列说法:
①若a+b+c=0,则b2﹣4ac>0;
②若方程两根为﹣1和2,则2a+c=0;
③若方程ax2+c=0有两个不相等的实根,则方程ax2+bx+c=0必有两个不相等的实根;
④若b=2a+c,则方程有两个不相等的实根.其中正确的有( )
A.①②③
B.①②④
C.②③④
D.①②③④
8.(2020秋?唐山期中)《代数学》中记载,形如x2+8x=33的方程,求正数解的几何方法是:“如图1,先构造一个面积为x2的正方形,再以正方形的边长为一边向外构造四个面积为2x的矩形,得到大正方形的面积为33+16=49,则该方程的正数解为7﹣4=3.”小聪按此方法解关于x的方程x2+10x+m=0时,构造出如图2所示的图形,已知阴影部分的面积为50,则该方程的正数解为( )
A.6
B.
C.2
D.55
9.(2020?衢州)某厂家2020年1~5月份的口罩产量统计如图所示.设从2月份到4月份,该厂家口罩产量的平均月增长率为x,根据题意可得方程( )
A.180(1﹣x)2=461
B.180(1+x)2=461
C.368(1﹣x)2=442
D.368(1+x)2=442
10.(2020春?西湖区校级月考)如果关于x的一元二次方程ax2+bx+c=0有两个实数根,且其中一个根为另一个根的两倍,则称这样的方程为“2倍根方程”,以下说法不正确的是( )
A.方程x2﹣3x+2=0是2倍根方程
B.若关于x的方程(x﹣2)(mx+n)=0是2倍根方程,则m+n=0
C.若m+n=0且m≠0,则关于x的方程(x﹣2)(mx+n)=0是2倍根方程
D.若2m+n=0且m≠0,则关于x的方程x2+(m﹣n)x﹣mn=0
是2倍根方程
二.填空题(共4小题)
11.(2021春?下城区期中)将x2﹣2x﹣2=0配方成(x+m)2=n的形式,则n=
.
12.(2021?海淀区校级模拟)如图,某小区规划在一个长30m、宽20m的长方形ABCD土地上修建三条同样宽的通道,使其中两条与AB平行,另一条与AD平行,其余部分种花草.要使每一块花草的面积都为78m2,那么通道的宽应设计成多少m?设通道的宽为xm,由题意列得方程
.
13.(2021春?余杭区期中)已知三角形两边的长分别是4和3,第三边的长是一元二次方程x2﹣8x+15=0的一个实数根,则该三角形的面积是
.
14.(2020?山西模拟)准备在一块长为30米,宽为24米的长方形花圃内修建四条宽度相等,且与各边垂直的小路,(如图所示)四条小路围成的中间部分恰好是一个正方形,且边长是小路宽度的4倍,若四条小路所占面积为80平方米,则小路的宽度为
米.
三.解答题(共16小题)
15.(2021春?余姚市校级期中)解方程:
(1)x2﹣6x=0;
(2)x2﹣2x=2x+1.
16.(2021春?拱墅区校级期中)解下列方程:
(1)x2﹣4x﹣1=0;
(2)3x2=8x.
17.(2021春?下城区期中)已知关于x的一元二次方程:x2﹣(2k+1)x+4(k)=0.
(1)求证:这个方程总有两个实数根;
(2)若等腰△ABC的一边长a=4,另两边长b、c,恰好是这个方程的两个实数根,求△ABC的周长.
(3)若方程的两个实数根之差等于3,求k的值.
18.(2021春?鹿城区校级期中)(1)计算:;
(2)解方程:x2﹣4x=5.
19.(2021春?余杭区期中)端年节吃粽子是中国古老的传统习俗,某粽子批发店卖出每个粽子的利润为2元,根据员工情况,每天最多能做1100个,由市场调查得知,若每个粽子的单价降低x元,则粽子每天的销售量y(个)关于x(元)的函数关系式为y=800x+400.
(1)若每个粽子降价0.2元,则该店每天的销售量为
个,每天的总利润为
元.
(2)当每个粽子的单价降低多少元时,该店每天的总利润刚好是1200元?
20.(2021春?拱墅区校级期中)解方程:
(1)7x(5x+2)=6(5x+2);
(2)x2﹣1.
21.(2021春?上城区校级期中)如图,利用一面墙(墙长25米),用总长度49米的栅栏(图中实线部分)围成一个矩形围栏ABCD,且中间共留两个1米的小门,设栅栏BC长为x米.
(1)AB=
米(用含x的代数式表示);
(2)若矩形围栏ABCD面积为210平方米,求栅栏BC的长;
(3)矩形围栏ABCD面积是否有可能达到240平方米?若有可能,求出相应x的值;若不可能,则说明理由.
22.(2021春?柯桥区月考)解方程:
(1)x2﹣6x﹣9=0;
(2)9(2x+3)2=16(1﹣3x)2.
23.(2020秋?鄄城县期末)用适当的方法求解下列方程:
(1)x2﹣2x﹣1=0;
(2)(x+4)2=5(x+4).
24.(2019秋?江北区校级期末)象山红美人柑橘是我省农科院研制的优质品种,宁波市某种植基地2017年种植“象山红美人”100亩,到2019年“象山红美人”的种植面积达到196亩.
(1)求该基地这两年“象山红美人”种植面积的平均增长率.
(2)市场调查发现,当“象山红美人”的售价为45元/千克时,每天能售出200千克,售价每降价1元,每天可多售出50千克,为了推广宣传,基地决定降价促销,同时减少库存,已知该基地“象山红美人”的平均成本价为33元/千克,若使销售“象山红美人”每天获利3150元,则售价应降低多少元?
25.(2020春?温州期末)疫情期间,某公司向厂家订购A,B两款洗手液共50箱.已知购买A款洗手液1箱进价为200元,在此基础上,所购买的A款洗手液数量每增加1箱,每箱进价降低2元.厂家为保障盈利,每次最多可订购30箱A款洗手液.B款洗手液的进价为每箱100元,设该公司购买A款洗手液x箱.
(1)根据信息填表:
型号
数量(箱)
进价(元/箱)
A
x
B
100
(2)若订购这批洗手液的总进价为6240元,则该公司订购了多少箱A款洗手液?
26.(2020春?湖州月考)若m是方程x2﹣2x﹣15=0的一个根,求代数式的值.
27.(2020春?越城区校级月考)如图,在△ABC中,∠B=90°,AB=12cm,BC=16cm.点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动,如果P、Q分别从A、B同时出发,当一个点到达终点时,另一个点也随之停止运动.设运动的时间为t秒.
(1)当t为何值时,△PBQ的面积等于35cm2?
(2)当t为何值时,PQ的长度等于8cm?
(3)若点P,Q的速度保持不变,点P在到达点B后返回点A,点Q在到达点C后返回点B,一个点停止,另一个点也随之停止.问:当t为何值时,△PBQ的面积等于32cm2?
28.(2020春?越城区校级期中)国商大厦某专柜销售一批名牌衬衫,平均每天可销售20件,每件盈利44元为了扩大销售,增加盈利,尽快减少库存,该专柜决定采取适当降价措施.经调查发现,如果每件衬衫每降价1元,专柜平均每天可多售出5件.求该专柜平均每天盈利1600元,且让顾客得到实惠,每件衬衫应降价多少元?
29.(2020秋?鹿城区校级月考)如图是小芳家2019年全年月用电量的条形统计图.据图中提供的信息,解答下列问题:
(1)2019年四个季度中小芳家用电量最大的是第
季度.
(2)求2019年5月至6月用电量的月增长率.
(3)今年(2020年)小芳家添置了新电器.已知今年5月份的用电量是120千瓦时,根据2019年5月至7月用电量的增长趋势,预计今年7月份的用电量将达到240千瓦时,假设今年5月至6月用电量月增长率是6月至7月用电量月增长率的1.5倍,据以上信息可求得小芳家今年6月份的用电量是
千瓦时(直接给出答案).
30.(2020春?上虞区期末)解答下列各题:
(1)用配方法解方程:x2﹣8x﹣4=0.
(2)已知一元二次方程2x2﹣mx﹣m=0的一个根是,求m的值和方程的另一个根.
2021年浙江八年级数学期末考试专题训练——专题2一元二次方程
参考答案与试题解析
一.选择题(共10小题)
1.【解答】解:∵关于x的一元二次方程(a﹣1)x2﹣2x﹣1=0有两个实数根,
∴△=(﹣2)2﹣4×(a﹣1)×(﹣1)=4a≥0,
解得a≥0,
又∵a﹣1≠0,
∴a≥0且a≠1,
故选:B.
2.【解答】解:∵x2﹣6x+3=0,
∴x2﹣6x=﹣3,
则x2﹣6x+9=﹣3+9,即(x﹣3)2=6,
∴x=﹣3,b=6,
故选:D.
3.【解答】解:∵x2﹣4x﹣1=0,
∴x2﹣4x=1,
则x2﹣4x+4=1+4,即(x﹣2)2=5,
∴m=﹣2,n=5,
故选:D.
4.【解答】解:①若a+b+c=0,则x=1是方程ax2+bx+c=0的解,
由一元二次方程的实数根与判别式的关系可知:△=b2﹣4a≥0,故①正确;
②方程ax2+c=0有两个不相等的实根,
∴△=0﹣4ac>0,
∴﹣4ac>0
则方程ax2+bx+c=0的判别式△=b2﹣4a>0,
∴方程ax2+bx+c=0必有两个不相等的实根,故②正确;
③∵c是方程ax2+bx+c=0的一个根,
则ac2+bc+c=0,
∴c(ac+b+1)=0,
若c=0,等式仍然成立,
但ac+b+1=0不一定成立,故③不正确;
④若x0是一元二次方程ax2+bx+c=0的根,
则由求根公式可得:x0,
∴2ax0+b,
∴b2﹣4ac=(2ax0+b)2,故④正确.
故正确的有①②④,
故选:A.
5.【解答】解:∵关于x的一元二次方程nx2x+2=0有两个不相等的实数根,
∴△=()2﹣4n×2>0且n≠0,4n+3≥0,
解得n且n≠0,
故选:C.
6.【解答】解:∵x2+2x﹣3=0,
∴x2+2x=3,
则x2+2x+1=3+1,即(x+1)2=4,
故选:B.
7.【解答】解:①若a+b+c=0,那么x=1为一个实数根.
如果原方程另一个实数根也是1,那么b2﹣4ac=0,
因此①错误;
②把x=﹣1代入方程得到:a﹣b+c=0
(1)
把x=2代入方程得到:4a+2b+c=0
(2)
把(2)式加(1)式×2得到:6a+3c=0,
即:2a+c=0,故正确;
③方程ax2+c=0有两个不相等的实数根,
则它的△=﹣4ac>0,
∴b2﹣4ac>0而方程ax2+bx+c=0的△=b2﹣4ac>0,
∴必有两个不相等的实数根.故正确;
④若b=2a+c则△=b2﹣4ac=(2a+c)2﹣4ac=4a2+c2,
∵a≠0,
∴4a2+c2>0故正确.
②③④都正确,
故选:C.
8.【解答】解:如图2,先构造一个面积为x2的正方形,再以正方形的边长为一边向外构造四个面积为x的矩形,得到大正方形的面积为:
504=50+25=75,
∴该方程的正数解为2=55.
故选:D.
9.【解答】解:从2月份到4月份,该厂家口罩产量的平均月增长率为x,根据题意可得方程:180(1+x)2=461,
故选:B.
10.【解答】解:A、解方程x2﹣3x+2=0得x1=1,x2=2,所以A选项的说法正确,不符合题意;
B、解方程得x1=2,x2,当2×2,则4m+n=0;当2,则m+n=0,所以B选项的说法错误,符合题意;
C、解方程得x1=2,x2,而m+n=0,则x2=1,所以C选项的说法正确,不符合题意;
D、解方程得x1=﹣m,x2=n,而2m+n=0,即n=﹣2m,所以x2=2x1,所以D选项的说法正确,不符合题意.
故选:B.
二.填空题(共4小题)
11.【解答】解:x2﹣2x=2,
x2﹣2x+1=3,
(x﹣1)2=3.
∴n=3.
故答案为:3.
12.【解答】解:由题意可得,
(30﹣2x)(20﹣x)=78×6,
化简,得
x2﹣35x+66=0,
故答案为:x2﹣35x+66=0.
13.【解答】解:解方程x2﹣8x+15=0,得x1=3,x2=5.
当x1=3时,与另两边组成等腰三角形,可求得底边4上的高为,所以该三角形的面积是42=2;
当x2=5时,与另两边组成直角三角形,该三角形的面积=3×4÷2=6.
14.【解答】解:设小路的宽度为x米,则小正方形的边长为4x米,
依题意得:(30+4x+24+4x)x=80
整理得:4x2+27x﹣40=0
解得x1=﹣8(舍去),x2.
故答案为:.
三.解答题(共16小题)
15.【解答】解:(1)x2﹣6x=0,
x(x﹣6)=0,
x=0或x﹣6=0,
解得:x1=0,x2=6;
(2)x2﹣2x=2x+1,
x2﹣4x﹣1=0,
∵b2﹣4ac=(﹣4)2﹣4×1×(﹣1)=16+4=20>0,
∴x,
解得:x1=2,x2=2.
16.【解答】解:(1)x2﹣4x﹣1=0,
∵b2﹣4ac=(﹣4)2﹣4×1×(﹣1)=16+4=20>0,
∴x,
解得:x1=2,x2=2;
(2)3x2=8x,
3x2﹣8x=0,
x(3x﹣8)=0,
x=0或3x﹣8=0,
解得:x1=0,x2;
17.【解答】解:(1)△=(2k+1)2﹣4×1×4(k)
=4k2﹣12k+9
=(2k﹣3)2,
∵无论k取何值,(2k﹣3)2≥0,
故这个方程总有两个实数根;
(2)由求根公式得x,
∴x1=2k﹣1,x2=2.
∵另两边长b、c,恰好是这个方程的两个实数根,
设b=2k﹣1,c=2,
当a,b为腰时,则a=b=4,即2k﹣1=4,计算得出k,
此时三角形周长为4+4+2=10;
当b,c为腰时,b=c=2,此时b+c=a,构不成三角形,
故此种情况不存在.
综上所述,△ABC周长为10.
(3)∵方程的两个实数根之差等于3,
∴,
解得:k=0或3.
18.【解答】解:(1)原式=22;
(2)∵x2﹣4x=5,
∴x2﹣4x﹣5=0,
则(x﹣5)(x+1)=0,
∴x﹣5=0或x+1=0,
解得x1=5,x2=﹣1.
19.【解答】解:(1)由题意可得:若每个粽子降价0.2元,则该店每天的销售量为800×0.2+400=560(个),
每天的总利润为:560×(2﹣0.2)=1008(元).
故答案是:560;1008;
(2)由题意,得(2﹣x)(800x+400)=1200,
解得:x=0.5或x=1.
当x=1时,y=800+400=1200>1100,超过每天可以制作的最大量,故不符合题意.
所以,当每个粽子的单价降低0.5元时,该店每天的总利润刚好是1200元.
20.【解答】解:(1)∵7x(5x+2)=6(5x+2),
∴(5x+2)(7x﹣6)=0,
则5x+2=0或7x﹣6=0,
解得x1,x2;
(2)∵(x﹣1)=(x+1)(x﹣1),
∴(x﹣1)(x﹣1)=0,
则x﹣1=0或x﹣1=0,
解得x1=1,x2.
21.【解答】解:(1)设篱笆BC长为x米,
∵篱笆的全长为49米,且中间共留两个1米的小门,
∴AB=49+2﹣3x=51﹣3x(米),
故答案为:(51﹣3x);
(2)依题意,得:(51﹣3x)x=210,
整理,得:x2﹣17x+70=0,
解得:x1=7,x2=10.
当x=7时,AB=51﹣3x=30>25,不合题意,舍去,
当x=10时,AB=51﹣3x=21,符合题意,
答:篱笆BC的长为10米;
(3)不可能,理由如下:
依题意,得:(51﹣3x)x=240,
整理得:x2﹣17x+80=0,
∵△=(﹣17)2﹣4×1×80=﹣31<0,
∴方程没有实数根,
∴矩形鸡舍ABCD面积不可能达到240平方米.
22.【解答】解:(1)∵x2﹣6x﹣9=0,
∴x2﹣6x=9,
则x2﹣6x+9=9+9,即(x﹣3)2=18,
∴x﹣3,
∴x1=3+3,x2=3﹣3;
(2)∵9(2x+3)2=16(1﹣3x)2,
∴3(2x+3)=4(1﹣3x)或3(2x+3)=﹣4(1﹣3x),
解得x1,x2.
23.【解答】解:(1)∵x2﹣2x﹣1=0,
∴x2﹣2x=1,
则x2﹣2x+1=1+1,即(x﹣1)2=2,
∴x﹣1=±,
∴,;
(2)∵(x+4)2=5(x+4),
∴(x+4)2﹣5(x+4)=0,
则(x+4)(x﹣1)=0,
∴x+4=0或x﹣1=0,
解得x1=﹣4,x2=1.
24.【解答】(1)设该基地这两年种植面积的平均增长率为x,
根据题意可得100(1+x)2=196,
解得x=0.4或﹣2.4(舍去),
答:平均增长率为40%.
(2)设售价应降低m元,
则每天的销量为(200+50m)千克.
根据题意可得(45﹣m﹣33)(200+50m)=3150
解得m=3或5.
答:售价应降低3元或5元.
25.【解答】解:(1)根据题意知,购买B款洗手液的数量是(50﹣x)箱,购买A款洗手液的进价为200﹣2(x﹣1)=(202﹣2x)元.
故答案是:50﹣x;202﹣2x;
(2)设该公司购买A款洗手液x箱,
根据题意知,(202﹣2x)x+100(50﹣x)=6240,
解得x1=31,x2=20.
∵最多可订购30箱A款洗手液,
∴x=20符合题意.
答:该公司购买A款洗手液20箱.
26.【解答】解:∵x2﹣2x﹣15=0,
∴(x﹣5)(x+3)=0.
∴x=5或x=﹣3.
由于m是方程的一个根,所以m=5或﹣3.
∵
2
2
=﹣2(3+m)﹣2
=﹣6﹣2m﹣2.
当m=5时,原代数式无意义;
当m=﹣3时,原式=﹣6﹣2×(﹣3)﹣2
=0﹣2
=﹣2.
27.【解答】解:根据题意知BP=AB﹣AP=12﹣t,BQ=2t.
(1)根据三角形的面积公式,得
PB?BQ=35,
t(12﹣t)=35,
t2﹣12t+35=0,
解得t1=5,t2=7.
故当t为5或7时,△PBQ的面积等于35cm2.
(2)设t秒后,PQ的长度等于8cm,根据勾股定理,得
PQ2=BP2+BQ2=(12﹣t)2+(2t)2=128,
5t2﹣24t+16=0,
解得t1,t2=4.
故当t为或4时,PQ的长度等于8cm.
(3)当0<t≤8时,
PB?BQ=32,即2t×(12﹣t)=32,
则t2﹣12t+32=0,
解得t1=4,t2=8.
当8<t≤12时,
则CQ=2t﹣16,BQ=BC﹣CQ=16﹣(2t﹣16)=32﹣2t,PB=12﹣t,
则△PBQ的面积PB?BQ(12﹣t)×(32﹣2t)=32,
解得:t=20或8(均舍去);
当12<t≤16时,
PB?BQ=32,
(16﹣t)(t﹣12)=32,
t2﹣28t+224=0,
△=282﹣4×1×224=﹣112<0,
故方程无实数根.
综上所述,当t为4或8时,△PBQ的面积等于32cm2.
28.【解答】解:设每件衬衫应降价x元,
根据题意,得
(44﹣x)(20+5x)=1600,
解得:x1=36,x2=4,
∵要尽快减少库存,
∴x=36,
答:每件衬衫应降价36元.
29.【解答】解:(1)①由小芳家2019年全年月用电量的条形统计图得:2019年四个季度中小芳家用电量最大的是第三季度.
故答案为:三;
(2)100%=65%,
答:2019年5月至6月用电量的月增长率为65%;
(3)设今年5月至6月用电量月增长率为1.5x,则6月至7月用电量月增长率的x,
根据题意列方程得:120(1+x)(1+1.5x)=240,
化简得3x2+5x﹣2=0,解得x1,x2=﹣2(不合题意舍去),
∴120×(1+1.5x)=120×(1+1.5)=180(千瓦时),
答:预计小芳家今年6月份的用电量是180千瓦时.
故答案为:180.
30.【解答】解:(1)x2﹣8x﹣4=0,
x2﹣8x=4,
x2﹣8x+16=4+16,
(x﹣4)2=20,
x﹣4,
x1=4+2,x2=4﹣2;
(2)设方程的另一个根是a,
∵一元二次方程2x2﹣mx﹣m=0的一个根是,
∴根据根与系数的关系得:a+(),a,
解得:m=1,a=1,
即m=1,方程的另一个根是1.
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
