第5章特殊的平行四边形 单元综合提升训练-2020-2021学年浙教版八年级数学下册(Word版 含解析)
文档属性
| 名称 | 第5章特殊的平行四边形 单元综合提升训练-2020-2021学年浙教版八年级数学下册(Word版 含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 373.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-04 00:00:00 | ||
图片预览



文档简介
2021年度浙教版八年级数学下册《第5章特殊的平行四边形》单元综合提升训练(附答案)
1.下列说法中,不正确的是( )
A.对角线互相垂直平分的四边形是菱形
B.对角线互相垂直的矩形是正方形
C.对角线互相平分的四边形是平行四边形
D.对角线相等的四边形是矩形
2.已知矩形的对角线长为10,两邻边之比为3:4,则矩形的面积为( )
A.50 B.48 C.24 D.12
3.在菱形ABCD中,若添加一个条件后,使它是正方形,则添加的条件可以是( )
A.AB=AD B.AB⊥BC C.AC⊥BD D.AC平分∠BAD
4.如图,在正方形ABCD中,E为对角线BD上一点,且BE=BC,则∠ACE=( )
A.20.5° B.30.5° C.21.5° D.22.5°
5.如图,?ABCD中的对角线AC,BD相交于点O,点E.F在BD上,且BE═DF,连接AE,EC,CF,FA,下列条件能判定四边形AECF为矩形的是( )
A.BE=EO B.EO=AC C.AC⊥BE D.AE=AF
6.如图,在矩形ABCD中,AC、BD相交于点O,AE平分∠BAD交BC于点E,若∠CAE=15°,则∠BOE的度数为( )
A.60° B.75° C.72° D.90°
7.如图,点P是正方形ABCD内位于对角线AC下方的一点,∠1=∠2,则∠BPC的度数为 °.
8.已知四边形ABCD是矩形,点E是矩形ABCD的边上的点,且EA=EC.若AB=6,AC=2,则DE的长是 .
9.如图,在菱形ABCD中,AB=4,∠ABC=45°,菱形ABCD的对角线交于点O,则△ABO的面积为 .
10.如图,矩形ABCD中,对角线AC、BD交于点O,AE⊥BD于点E,若AB=6,OD=5,则AE= .
11.如图,O是矩形ABCD的对角线AC的中点,M是AD的中点,若OM=1,BC=4,则OB的长为 .
12.如图,正方形ABCD中,AE=2cm,CG=5cm.长方形EFGD的面积是11,四边形NGDH和MEDQ都是正方形,PQDH是长方形,则图中阴影部分的面积是 cm2.
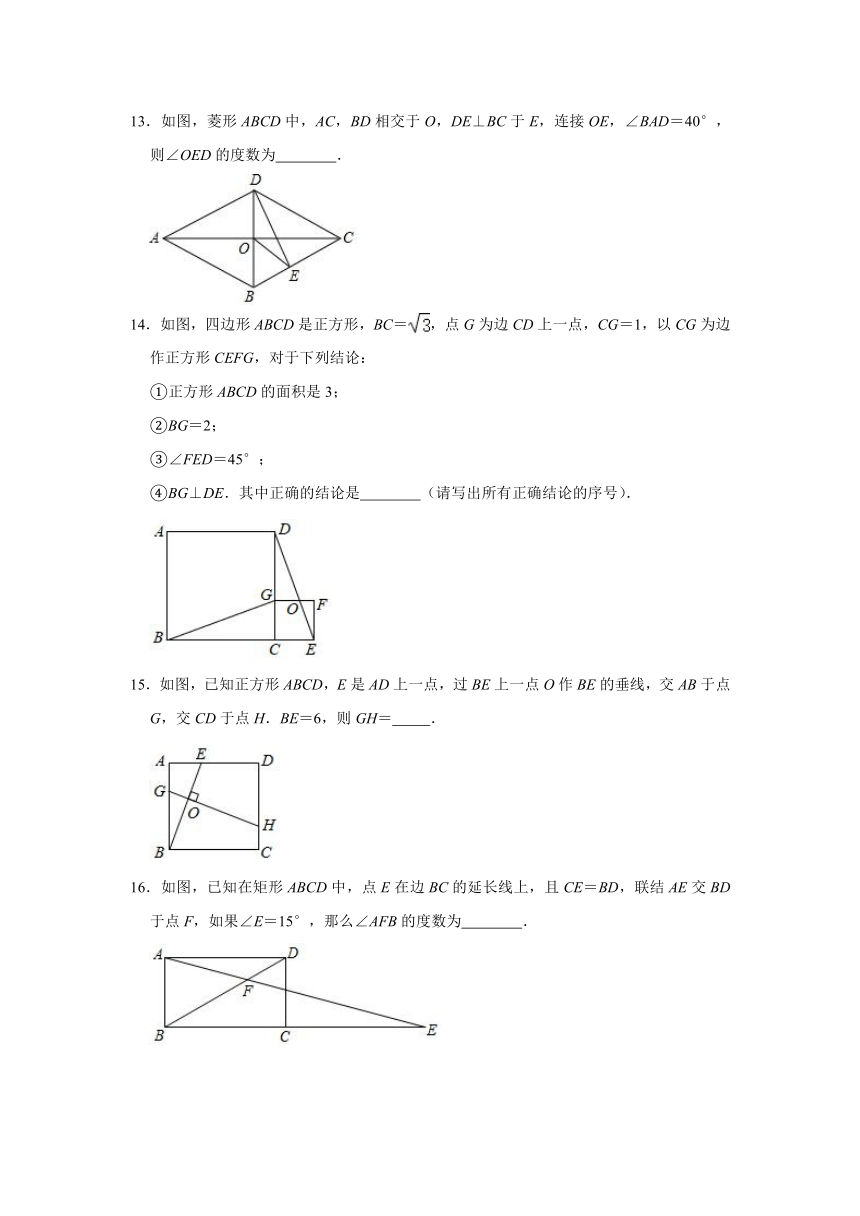
13.如图,菱形ABCD中,AC,BD相交于O,DE⊥BC于E,连接OE,∠BAD=40°,则∠OED的度数为 .
14.如图,四边形ABCD是正方形,BC=,点G为边CD上一点,CG=1,以CG为边作正方形CEFG,对于下列结论:
①正方形ABCD的面积是3;
②BG=2;
③∠FED=45°;
④BG⊥DE.其中正确的结论是 (请写出所有正确结论的序号).
15.如图,已知正方形ABCD,E是AD上一点,过BE上一点O作BE的垂线,交AB于点G,交CD于点H.BE=6,则GH= .
16.如图,已知在矩形ABCD中,点E在边BC的延长线上,且CE=BD,联结AE交BD于点F,如果∠E=15°,那么∠AFB的度数为 .
17.如图,正方形ABCD中,点E在BC上,EF⊥AC,EG⊥BD,垂足分别为F、G,若AC=4,则EF+EG= .
18.矩形ABCD中,对角线AC,BD相交于点O,AE⊥BD于点E,若OE=OD,则∠AOB的度数为 .
19.如图,在Rt△ABC中,∠A=90°,AB=6,BC=10,P是BC边上的一点,作PE垂直AB,PF垂直AC,垂足分别为E、F,求EF的最小值是 .
20.已知:如图,在四边形ABCD中,AC为对角线,AD∥BC,BC=2AD,∠BAC=90°,过点A作AE∥DC交BC于点E.
(1)求证:四边形AECD为菱形;
(2)若AB=AE=2,求四边形AECD的面积.
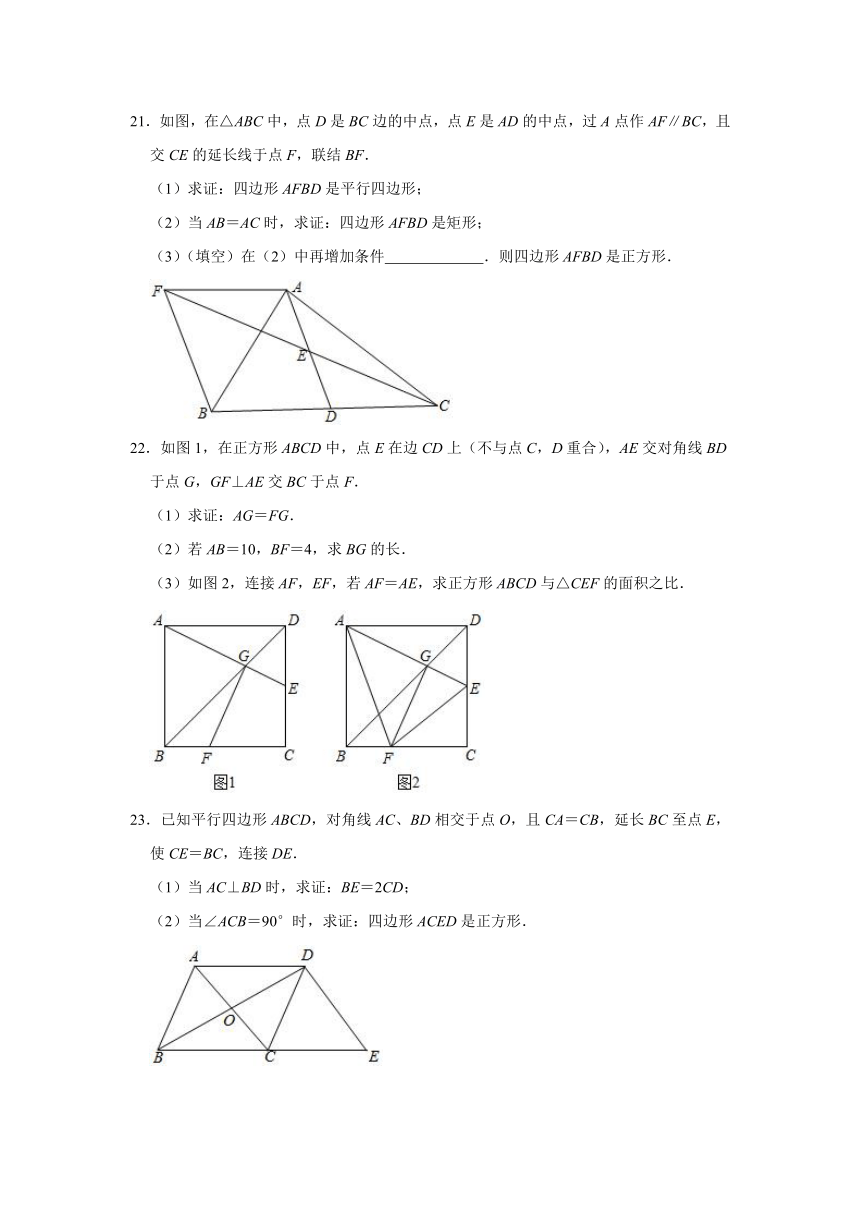
21.如图,在△ABC中,点D是BC边的中点,点E是AD的中点,过A点作AF∥BC,且交CE的延长线于点F,联结BF.
(1)求证:四边形AFBD是平行四边形;
(2)当AB=AC时,求证:四边形AFBD是矩形;
(3)(填空)在(2)中再增加条件 .则四边形AFBD是正方形.
22.如图1,在正方形ABCD中,点E在边CD上(不与点C,D重合),AE交对角线BD于点G,GF⊥AE交BC于点F.
(1)求证:AG=FG.
(2)若AB=10,BF=4,求BG的长.
(3)如图2,连接AF,EF,若AF=AE,求正方形ABCD与△CEF的面积之比.
23.已知平行四边形ABCD,对角线AC、BD相交于点O,且CA=CB,延长BC至点E,使CE=BC,连接DE.
(1)当AC⊥BD时,求证:BE=2CD;
(2)当∠ACB=90°时,求证:四边形ACED是正方形.
24.如图,在?ABCD中,对角线AC、BD相交于点O,AC⊥AB,∠AOB=60°.点E、点F分别是OB、OD的中点,连接AE、EC、CF、FA.
(1)求证:四边形AECF为矩形;
(2)若AB=3,求矩形AECF的面积.
25.如图,在正方形ABCD中,E、F分别是BC、CD边上的点,∠EAF=45°.
(1)如图(1),试判断EF,BE,DF间的数量关系,并说明理由;
(2)如图(2),若AH⊥EF于点H,试判断线段AH与AB的数量关系,并说明理由.
26.如图,在正方形ABCD中,点G在对角线BD上(不与点B,D重合),GE⊥DC于点E,GF⊥BC于点F,连接AG.若正方形ABCD的边长为2,∠AGF=105°.
(1)求∠BAG的度数;
(2)线段EF的长.
27.如图,在正方形ABCD中,点E是对角线BD上的一点(DE<BE),连接AE,过点E分别作EF⊥AE交BC于点F,EG⊥BD交BC的延长线于点G.
(1)若AD=2,DE=1,求EG的长度;
(2)求证:FG=AB.
28.如图,四边形ABCD中,已知AB⊥BC,CD⊥BC,且AB=CD.
(1)求证:四边形ABCD为矩形;
(2)对角线AC,BD相交于O,AE⊥BD,垂足为E,已知AB=3,AD=4,求△AEO的面积.
参考答案
1.解:A、对角线互相垂直平分的四边形是菱形,选项说法正确;
B、对角线互相垂直的矩形是正方形,选项说法正确;
C、对角线互相平分的四边形是平行四边形,选项说法正确;
D、对角线互相平分且相等的四边形是矩形,选项说法错误;
故选:D.
2.解:∵矩形的两邻边之比为3:4,
∴设矩形的两邻边长分别为:3x,4x,
∵对角线长为10,
∴(3x)2+(4x)2=102,
解得:x=2,
∴矩形的两邻边长分别为:6,8;
∴矩形的面积为:6×8=48.
故选:B.
3.解:根据对角线相等的菱形是正方形,可添加:AC=BD;
根据有一个角是直角的菱形是正方形,可添加的:∠ABC=90°,即AB⊥BC;
故添加的条件为:AC=BD或∠ABC=90°或AB⊥BC.
故选:B.
4.解:设AC与BD交于点O,
在四边形ABCD中,∠EOC=90°,∠1=∠2=45°.
∵BE=BC,
∴∠3=∠ECB=67.5°.
∴∠ACE=OCE=90°﹣∠3=90°﹣67.5°=22.5°.
故选:D.
5.解:∵四边形ABCD是平行四边形,
∴OA=OC=AC,OB=OD,
∵BE=DF,
∴OB﹣BE=OD﹣DF,即OE=OF,
∴四边形AECF是平行四边形,
A、BE=EO时,不能判定四边形AECF为矩形;故选项A不符合题意;
B、EO=AC时,EF=AC,
∴四边形AECF为矩形;故选项B符合题意;
C、AC⊥BE时,四边形AECF为菱形;故选项C不符合题意;
D、AE=AF时,四边形AECF为菱形;故选项D不符合题意;
故选:B.
6.解:∵在矩形ABCD中,AE平分∠BAD,
∴∠BAE=∠EAD=45°,AD∥BC,OA=OB,
∴∠AEB=∠EAD=45°,
∴BE=BA.
∵∠CAE=15°,∠BAE=45°,
∴∠BAC=60°,
又∵OA=OB,
∴△OAB为等边三角形,
∴BO=BA,
∴BO=BE,
∴∠BOE=∠BEO,
∵△OAB为等边三角形,
∴∠ABO=60°,
∴∠OBE=90°﹣60°=30°,
∴∠BOE=(180°﹣30°)÷2=75°.
故选:B.
7.解:∵四边形ABCD是正方形,
∴∠ACB=∠BAC=45°,
∴∠2+∠BCP=45°,
∵∠1=∠2,
∴∠1+∠BCP=45°,
∵∠BPC=180°﹣∠1﹣∠BCP,
∴∠BPC=135°,
故答案为:135.
8.解:如图,
∵四边形ABCD是矩形,
∴CD=AB=6,AD=BC,∠ABC=∠ADC=90°,
∴BC===2,
∴AD=2,
当点E在CD上时,
∵AE2=DE2+AD2=EC2,
∴(6﹣DE)2=DE2+4,
∴DE=;
当点E'在AB上时,
∵CE'2=BE'2+BC2=E'A2,
∴AE'2=(6﹣AE')2+4,
∴AE'=,
∴DE'===,
综上所述:DE=或,
故答案为:或.
9.解:如图,过点A作AE⊥BC于E,
∵∠ABC=45°,AE⊥BC,
∴∠ABC=∠BAE=45°,
∴AE=BE,
∵AE2+BE2=AB2=16,
∴AE=BE=2,
∵四边形ABCD是菱形,
∴AB=BC=4,S△ABO=S菱形ABCD,
∵菱形ABCD的面积=BC×AE=4×2=8,
∴S△ABO=S菱形ABCD=2,
故答案为:2.
10.解:∵四边形ABCD是矩形,
∴OB=OD=5,∠BAD=90°,
∴BD=10,
∴AD===8,
∵S△ABD=×AB×AD=×BD×AE,
∴AE==,
故答案为:;
11.解:∵O是矩形ABCD的对角线AC的中点,
∴OA=OC,AD=BC=4,∠ABC=90°,
又∵点M是AD的中点,
∴CD=2OM=2,
∴AC===2,
∵∠ABC=90°,AO=CO,
∴BO=AC=,
故答案为:.
12.解:设正方形ABCD的边长为xcm,
由题意DE=x﹣2(cm),DG=x﹣5(cm),则(x﹣2)(x﹣5)=11,
∴x2﹣7x=1
∵四边形NGDH和MEDQ都是正方形,
∴DE=ME=x﹣2(cm),DG=DH=x﹣5(cm),
∴MF=x﹣2+x﹣5=2x﹣7(cm),
∴图中阴影部分的面积=(2x﹣7)2=4x2﹣28x+49=4(x2﹣7x)+49=4+49=53(cm2),
故答案为:53.
13.解:∵四边形ABCD是菱形,∠BAD=40°,
∴∠DAO=BAD=20°,AC⊥BD,DO=BO,AD∥BC,
∴∠DOA=90°,
∴∠ADO=90°﹣∠DAO=70°,
∵AD∥BC,DE⊥BC,
∴DE⊥AD,
∴∠ADE=90°,
∴∠ODE=∠AD∠E﹣∠ADO=20°,
∵DE⊥BC,
∴∠DEB=90°,
∵DO=BO,
∴OE=BD=OD,
∴∠OED=∠ODE=20°,
故答案为:20°.
14.解:∵四边形ABCD是正方形,BC=,
∴BC=CD,∠BCD=90°,正方形ABCD的面积=BC2=3,故①正确;
∵BC=,CG=1,
∴BG===2,故②正确,
如图,连接GE,延长BG交DE于H,
∵四边形CEFG是正方形,
∴CG=CE,∠GCE=∠BCG=90°,∠GEF=45°,
∵∠FED<∠GEF,
∴∠FED<45°,故③错误,
∵CG=CE,∠GCE=∠BCG=90°,BC=CD,
∴△BCG≌△DCE(SAS),
∴∠GBC=∠CDE,
∵∠CDE+∠DEC=90°,
∴∠GBC+∠DEC=90°,
∴∠BHE=90°,
∴BH⊥DE,故④正确,
故答案为:①②④.
15.解:过点A作GH的平行线,交DC于点H′,交BE于点O',如图所示:
∵ABCD是正方形,
∴AG∥H′H,BA=AD,∠BAE=∠D=90°,
∴∠H′AD+∠AH′D=90°,
∵GH⊥BE,AH′∥GH,
∴AH′⊥BE,
∴∠H′AD+∠BEA=90°,
∴∠BEA=∠AH′D,
在△BAE和△ADH′中,,
∴△BAE≌△ADH′(AAS),
∴BE=AH′,
∵AG∥H′H,AH′∥GH,
∴四边形AH′HG是平行四边形,
∴GH=AH′,
∴GH=BE=6,
故答案为:6.
16.解:连接AC交BD于点O,如图所示:
∵四边形ABCD是矩形,
∴OA=OC=AC,OB=OD=BD,AC=BD,
∴OB=OC,
∴∠OBC=∠OCB,
∵CE=BD,
∴AC=CE,
∴∠CAE=∠E=15°,
∴∠OBC=∠OCB=∠CAE+∠E=30°,
∴∠AFB=∠OBC+∠E=30°+15°=45°;
故答案为:45°.
17.解:∵正方形ABCD,AC=4,
∴∠ACB=45°,BD⊥AC,OC==2,
∵EF⊥AC,EG⊥OB,
∴∠OFE=∠OGE=∠BOC=90°,
∴四边形GEFO为矩形,△CEF为等腰直角三角形,
∴EF=CF,EG=OF,
∴EF+EG=CF+OF=OC=2.
故答案为:2.
18.解:∵矩形ABCD,
∴OB=OD,
∵AE⊥BD于点E,OE=OD,
∴OE=OB,
∴△OAB是等腰三角形,
∴AB=OA=OB,
∴△OAB是等边三角形,
∴∠AOB=60°,
180°﹣60°=120°,
故答案为:60°或120°.
19.解:连接AP,
∵∠BAC=90°,PE⊥AB,PF⊥AC,
∴∠BAC=∠AEP=∠AFP=90°,
∴四边形AFPE是矩形,
∴EF=AP,
要使EF最小,只要AP最小即可,
当AP⊥BC时,AP最小,
在Rt△BAC中,∠BAC=90°,AB=6,BC=10,
由勾股定理得:AC===8,
由三角形面积公式得:△ABC的面积=×AB×AC=×BC×AP,
∴AP===4.8,
即EF=4.8,
故答案为:4.8.
20.解:(1)∵AD∥BC,AE∥DC,
∴四边形AECD为平行四边形,
∴AD=EC,
∵BC=2AD,
∴BC=2EC.
∴E为BC的中点
∵∠BAC=90°,
∴BC=2AE
∴AE=EC,
∵四边形AECD为平行四边形,
∴四边形AECD为菱形;
(2)解:连接DE,
∵AB=AE=2,AE=BE,
∴AB=AE=BE=2,
∴△ABE是等边三角形.
∴∠B=60°.
∵AD=BE,AD∥BC,
∴四边形ABED为平行四边形.
∴DE=AB=2,
∵∠B=60°,∠BAC=90°,AB=2,
∴BC=4.
∴.
∴SAECD==2.
21.(1)证明:∵点D是BC边的中点,点E是AD的中点,
∴DE是△BCF的中位线,
∴DE∥BF,
∴AD∥BF,
∵AF∥BC,
∴四边形AFBD是平行四边形;
(2)证明:(2)∵AB=AC,BD=DC,
∴AD⊥BC.
∴∠ADB=90°.
∵四边形AFBD是平行四边形,
∴四边形AFBD是矩形;
(3)当△ABC为等腰直角三角形,且∠BAC=90°时,四边形AFBD是正方形,理由如下:
∵四边形AFBD为平行四边形,
又∵等腰直角三角形ABC,且D为BC的中点,
∴AD=BD,∠ABD=90°,
∴四边形AFBD为正方形.
故答案为:∠BAC=90°.
22.证明:(1)连接GC,
∵四边形ABCD是正方形,
∴AB=BC,∠ABC=90°,∠ABD=∠CBD=45°,
又∵BG=BG,
∴△ABG≌△CBG(SAS),
∴AG=CG,∠BAG=∠BCG,
∵∠ABC+∠BAG+∠AGF+∠BFG=360°,且∠ABC=∠AGF=90°,
∴∠BAG+∠BFG=180°,
∴∠BCG+∠BFG=180°,
∵∠BFG+∠GFC=180°,
∴∠BCG=∠GFC,
∴GC=GF,
∴AG=FG;
(2)如图2,过点G作GH⊥BC于H,
∵AB=10,BF=4,
∴AF2=AB2+BF2=AG2+GF2,
∴GF2=58,
∵∠DBC=45°,GH⊥BC,
∴BH=GH,BG=GH,
∵GF2=GH2+FH2,
∴58=GH2+(GH﹣4)2,
∴GH=7,(负值舍去),
∴BG=7;
(3)如图,在AB上截取BF=BN,连接NF,
∵AG=GF,AG⊥GF,
∴∠EAF=45°,
∵AE=AF,AB=AD,
∴Rt△ABF≌Rt△ADE(HL),
∴∠BAF=∠DAE=22.5°,BF=DE,
∴CF=CE,
∵BF=BN,∠ABC=90°,
∴NF=BF,∠BNF=∠BFN=45°,
∴∠BAF=∠AFN=22.5°,
∴AN=NF=BF,
∵AB=BC,
∴BN+AN=BF+FC,
∴FC=BF,
∴BC=(+1)BF,
∴正方形ABCD与△CEF的面积之比=BC2:FC2=3+2:1.
23.(1)证明:∵四边形ABCD是平行四边形,
又∵AC⊥BD,
∴四边形ABCD是菱形.
∴BC=CD.
又∵CE=BC,
∴BE=2BC,
∴BE=2CD;
(2)证明:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BE,
又∵CE=BC,
∴AD=CE,AD∥CE,
∴四边形ACED是平行四边形.
∵∠ACB=90°,
∴平行四边形ACED是矩形,
又∵CA=CB,
∴CA=CE,
∴矩形ACED是正方形.
24.(1)证明:∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵点E、点F分别是OB、OD的中点,
∴OE=OB,OF=OD,
∴OE=OF,
∴四边形AECF是平行四边形,
∵AC⊥AB,∠AOB=60°,
∴∠ABO=30°,
∴OA=OB=OE,
∴AC=EF,
∴四边形AECF为矩形;
(2)解:由(1)得:OA=OE=OC=OF,∠AOB=60°,∠ABO=30°,
∴△OAE是等边三角形,∠OFA=∠OAF=30°=∠ABO,
∴AE=OA,AF=AB=3,
∵AC⊥AB,
∴∠OAB=90°,
∴AE=OA=AB=,
∴矩形AECF的面积=AF×AE=3.
25.(1)解:BE+DF=EF;理由如下:
如图1,延长FD到G,使DG=BE,连接AG,
∵在△GDA和△EBA中,
,
∴△GDA≌△EBA(SAS),
∴AG=AE,∠GAD=∠EAB,
故∠GAF=45°,
在△GAF和△EAF中,
∵,
∴△GAF≌△EAF(SAS),
∴GF=EF,
即GD+DF=BE+DF=EF;
(2)AH=AB,理由如下:
∵四边形ABCD为正方形,
∴AB=AD,∠BAD=90°,
∴把△ADF绕点A顺时针旋转90°得到△ABQ,如图2,
∴AQ=AF,∠FAQ=90°,∠ABQ=∠D=90°,
而∠ABC=90°,
∴点Q在CB的延长线上,
∵∠EAF=45°,
∴∠QAE=90°﹣∠EAF=45°,
∴∠EAF=∠QAE,
在△AEQ和△AEF中,
,
∴△AEQ≌△AEF(SAS),
∴EQ=EF,
∵AB⊥EQ,AH⊥FE,
∴AB=AH.
26.解:(1)∵四边形ABCD是正方形,
∴∠DBC=∠ABG=45°,AB=BC=CD=2,
∵GF⊥BC,
∴∠GBF=45°=∠BGF,
∵∠AGF=105°,
∴∠AGB=60°,
∵∠AGB+∠BAG+∠ABG=180°,
∴∠BAG=180°﹣45°﹣60°=75°;
(2)如图,连接CG,过点A作AH⊥BD于点H,
∵四边形ABCD是正方形,
∴A、C关于对角线BD对称,
∵点G在BD上,
∴GA=GC,
∵GE⊥DC于点E,GF⊥BC于点F,
∴∠GEC=∠ECF=∠CFG=90°,
∴四边形EGFC是矩形,
∴EF=GC,
∴AG=EF,
∵AB=2,∠ABH=45°,AH⊥BG,
∴BH=AH=,
∵∠AGB=60°,AH⊥BG,AH=,
∴,AG=2HG=,
∴EF=.
27.解:(1)∵四边形ABCD是正方形,
∴AD=AB=2,BD=AD=2,∠ABD=∠CBD=45°,
∴BE=BD﹣DE=2﹣1,
∵EG⊥BD,∠DBG=45°,
∴∠DBG=∠EGB=45°,
∴EB=EG=2﹣1;
(2)∵AE⊥EF,
∴∠AEF=∠BEG=90°,
∴∠AEB=∠GEF,
又∵BE=EG,∠ABD=∠FGE=45°,
∴△ABE≌△FGE(AAS),
∴FG=AB.
28.(1)证明:∵AB⊥BC,CD⊥BC,
∴AB∥CD,
∵AB=CD,
∴四边形ABCD是平行四边形,
∵AB⊥BC,
∴∠ABC=90°,
∴四边形ABCD为矩形;
(2)解:∵四边形ABCD为矩形,
∴∠BAC=90°,
∵AB=3,AD=4,
∴BD=5,
∵S△ABD=AB?AD=BD?AE,
∴3×4=5AE,
∴AE=,
∵AC=BD=5,
∴AO=AC=,
∵AE⊥BD,
∴OE===,
∴△AEO的面积==.
1.下列说法中,不正确的是( )
A.对角线互相垂直平分的四边形是菱形
B.对角线互相垂直的矩形是正方形
C.对角线互相平分的四边形是平行四边形
D.对角线相等的四边形是矩形
2.已知矩形的对角线长为10,两邻边之比为3:4,则矩形的面积为( )
A.50 B.48 C.24 D.12
3.在菱形ABCD中,若添加一个条件后,使它是正方形,则添加的条件可以是( )
A.AB=AD B.AB⊥BC C.AC⊥BD D.AC平分∠BAD
4.如图,在正方形ABCD中,E为对角线BD上一点,且BE=BC,则∠ACE=( )
A.20.5° B.30.5° C.21.5° D.22.5°
5.如图,?ABCD中的对角线AC,BD相交于点O,点E.F在BD上,且BE═DF,连接AE,EC,CF,FA,下列条件能判定四边形AECF为矩形的是( )
A.BE=EO B.EO=AC C.AC⊥BE D.AE=AF
6.如图,在矩形ABCD中,AC、BD相交于点O,AE平分∠BAD交BC于点E,若∠CAE=15°,则∠BOE的度数为( )
A.60° B.75° C.72° D.90°
7.如图,点P是正方形ABCD内位于对角线AC下方的一点,∠1=∠2,则∠BPC的度数为 °.
8.已知四边形ABCD是矩形,点E是矩形ABCD的边上的点,且EA=EC.若AB=6,AC=2,则DE的长是 .
9.如图,在菱形ABCD中,AB=4,∠ABC=45°,菱形ABCD的对角线交于点O,则△ABO的面积为 .
10.如图,矩形ABCD中,对角线AC、BD交于点O,AE⊥BD于点E,若AB=6,OD=5,则AE= .
11.如图,O是矩形ABCD的对角线AC的中点,M是AD的中点,若OM=1,BC=4,则OB的长为 .
12.如图,正方形ABCD中,AE=2cm,CG=5cm.长方形EFGD的面积是11,四边形NGDH和MEDQ都是正方形,PQDH是长方形,则图中阴影部分的面积是 cm2.
13.如图,菱形ABCD中,AC,BD相交于O,DE⊥BC于E,连接OE,∠BAD=40°,则∠OED的度数为 .
14.如图,四边形ABCD是正方形,BC=,点G为边CD上一点,CG=1,以CG为边作正方形CEFG,对于下列结论:
①正方形ABCD的面积是3;
②BG=2;
③∠FED=45°;
④BG⊥DE.其中正确的结论是 (请写出所有正确结论的序号).
15.如图,已知正方形ABCD,E是AD上一点,过BE上一点O作BE的垂线,交AB于点G,交CD于点H.BE=6,则GH= .
16.如图,已知在矩形ABCD中,点E在边BC的延长线上,且CE=BD,联结AE交BD于点F,如果∠E=15°,那么∠AFB的度数为 .
17.如图,正方形ABCD中,点E在BC上,EF⊥AC,EG⊥BD,垂足分别为F、G,若AC=4,则EF+EG= .
18.矩形ABCD中,对角线AC,BD相交于点O,AE⊥BD于点E,若OE=OD,则∠AOB的度数为 .
19.如图,在Rt△ABC中,∠A=90°,AB=6,BC=10,P是BC边上的一点,作PE垂直AB,PF垂直AC,垂足分别为E、F,求EF的最小值是 .
20.已知:如图,在四边形ABCD中,AC为对角线,AD∥BC,BC=2AD,∠BAC=90°,过点A作AE∥DC交BC于点E.
(1)求证:四边形AECD为菱形;
(2)若AB=AE=2,求四边形AECD的面积.
21.如图,在△ABC中,点D是BC边的中点,点E是AD的中点,过A点作AF∥BC,且交CE的延长线于点F,联结BF.
(1)求证:四边形AFBD是平行四边形;
(2)当AB=AC时,求证:四边形AFBD是矩形;
(3)(填空)在(2)中再增加条件 .则四边形AFBD是正方形.
22.如图1,在正方形ABCD中,点E在边CD上(不与点C,D重合),AE交对角线BD于点G,GF⊥AE交BC于点F.
(1)求证:AG=FG.
(2)若AB=10,BF=4,求BG的长.
(3)如图2,连接AF,EF,若AF=AE,求正方形ABCD与△CEF的面积之比.
23.已知平行四边形ABCD,对角线AC、BD相交于点O,且CA=CB,延长BC至点E,使CE=BC,连接DE.
(1)当AC⊥BD时,求证:BE=2CD;
(2)当∠ACB=90°时,求证:四边形ACED是正方形.
24.如图,在?ABCD中,对角线AC、BD相交于点O,AC⊥AB,∠AOB=60°.点E、点F分别是OB、OD的中点,连接AE、EC、CF、FA.
(1)求证:四边形AECF为矩形;
(2)若AB=3,求矩形AECF的面积.
25.如图,在正方形ABCD中,E、F分别是BC、CD边上的点,∠EAF=45°.
(1)如图(1),试判断EF,BE,DF间的数量关系,并说明理由;
(2)如图(2),若AH⊥EF于点H,试判断线段AH与AB的数量关系,并说明理由.
26.如图,在正方形ABCD中,点G在对角线BD上(不与点B,D重合),GE⊥DC于点E,GF⊥BC于点F,连接AG.若正方形ABCD的边长为2,∠AGF=105°.
(1)求∠BAG的度数;
(2)线段EF的长.
27.如图,在正方形ABCD中,点E是对角线BD上的一点(DE<BE),连接AE,过点E分别作EF⊥AE交BC于点F,EG⊥BD交BC的延长线于点G.
(1)若AD=2,DE=1,求EG的长度;
(2)求证:FG=AB.
28.如图,四边形ABCD中,已知AB⊥BC,CD⊥BC,且AB=CD.
(1)求证:四边形ABCD为矩形;
(2)对角线AC,BD相交于O,AE⊥BD,垂足为E,已知AB=3,AD=4,求△AEO的面积.
参考答案
1.解:A、对角线互相垂直平分的四边形是菱形,选项说法正确;
B、对角线互相垂直的矩形是正方形,选项说法正确;
C、对角线互相平分的四边形是平行四边形,选项说法正确;
D、对角线互相平分且相等的四边形是矩形,选项说法错误;
故选:D.
2.解:∵矩形的两邻边之比为3:4,
∴设矩形的两邻边长分别为:3x,4x,
∵对角线长为10,
∴(3x)2+(4x)2=102,
解得:x=2,
∴矩形的两邻边长分别为:6,8;
∴矩形的面积为:6×8=48.
故选:B.
3.解:根据对角线相等的菱形是正方形,可添加:AC=BD;
根据有一个角是直角的菱形是正方形,可添加的:∠ABC=90°,即AB⊥BC;
故添加的条件为:AC=BD或∠ABC=90°或AB⊥BC.
故选:B.
4.解:设AC与BD交于点O,
在四边形ABCD中,∠EOC=90°,∠1=∠2=45°.
∵BE=BC,
∴∠3=∠ECB=67.5°.
∴∠ACE=OCE=90°﹣∠3=90°﹣67.5°=22.5°.
故选:D.
5.解:∵四边形ABCD是平行四边形,
∴OA=OC=AC,OB=OD,
∵BE=DF,
∴OB﹣BE=OD﹣DF,即OE=OF,
∴四边形AECF是平行四边形,
A、BE=EO时,不能判定四边形AECF为矩形;故选项A不符合题意;
B、EO=AC时,EF=AC,
∴四边形AECF为矩形;故选项B符合题意;
C、AC⊥BE时,四边形AECF为菱形;故选项C不符合题意;
D、AE=AF时,四边形AECF为菱形;故选项D不符合题意;
故选:B.
6.解:∵在矩形ABCD中,AE平分∠BAD,
∴∠BAE=∠EAD=45°,AD∥BC,OA=OB,
∴∠AEB=∠EAD=45°,
∴BE=BA.
∵∠CAE=15°,∠BAE=45°,
∴∠BAC=60°,
又∵OA=OB,
∴△OAB为等边三角形,
∴BO=BA,
∴BO=BE,
∴∠BOE=∠BEO,
∵△OAB为等边三角形,
∴∠ABO=60°,
∴∠OBE=90°﹣60°=30°,
∴∠BOE=(180°﹣30°)÷2=75°.
故选:B.
7.解:∵四边形ABCD是正方形,
∴∠ACB=∠BAC=45°,
∴∠2+∠BCP=45°,
∵∠1=∠2,
∴∠1+∠BCP=45°,
∵∠BPC=180°﹣∠1﹣∠BCP,
∴∠BPC=135°,
故答案为:135.
8.解:如图,
∵四边形ABCD是矩形,
∴CD=AB=6,AD=BC,∠ABC=∠ADC=90°,
∴BC===2,
∴AD=2,
当点E在CD上时,
∵AE2=DE2+AD2=EC2,
∴(6﹣DE)2=DE2+4,
∴DE=;
当点E'在AB上时,
∵CE'2=BE'2+BC2=E'A2,
∴AE'2=(6﹣AE')2+4,
∴AE'=,
∴DE'===,
综上所述:DE=或,
故答案为:或.
9.解:如图,过点A作AE⊥BC于E,
∵∠ABC=45°,AE⊥BC,
∴∠ABC=∠BAE=45°,
∴AE=BE,
∵AE2+BE2=AB2=16,
∴AE=BE=2,
∵四边形ABCD是菱形,
∴AB=BC=4,S△ABO=S菱形ABCD,
∵菱形ABCD的面积=BC×AE=4×2=8,
∴S△ABO=S菱形ABCD=2,
故答案为:2.
10.解:∵四边形ABCD是矩形,
∴OB=OD=5,∠BAD=90°,
∴BD=10,
∴AD===8,
∵S△ABD=×AB×AD=×BD×AE,
∴AE==,
故答案为:;
11.解:∵O是矩形ABCD的对角线AC的中点,
∴OA=OC,AD=BC=4,∠ABC=90°,
又∵点M是AD的中点,
∴CD=2OM=2,
∴AC===2,
∵∠ABC=90°,AO=CO,
∴BO=AC=,
故答案为:.
12.解:设正方形ABCD的边长为xcm,
由题意DE=x﹣2(cm),DG=x﹣5(cm),则(x﹣2)(x﹣5)=11,
∴x2﹣7x=1
∵四边形NGDH和MEDQ都是正方形,
∴DE=ME=x﹣2(cm),DG=DH=x﹣5(cm),
∴MF=x﹣2+x﹣5=2x﹣7(cm),
∴图中阴影部分的面积=(2x﹣7)2=4x2﹣28x+49=4(x2﹣7x)+49=4+49=53(cm2),
故答案为:53.
13.解:∵四边形ABCD是菱形,∠BAD=40°,
∴∠DAO=BAD=20°,AC⊥BD,DO=BO,AD∥BC,
∴∠DOA=90°,
∴∠ADO=90°﹣∠DAO=70°,
∵AD∥BC,DE⊥BC,
∴DE⊥AD,
∴∠ADE=90°,
∴∠ODE=∠AD∠E﹣∠ADO=20°,
∵DE⊥BC,
∴∠DEB=90°,
∵DO=BO,
∴OE=BD=OD,
∴∠OED=∠ODE=20°,
故答案为:20°.
14.解:∵四边形ABCD是正方形,BC=,
∴BC=CD,∠BCD=90°,正方形ABCD的面积=BC2=3,故①正确;
∵BC=,CG=1,
∴BG===2,故②正确,
如图,连接GE,延长BG交DE于H,
∵四边形CEFG是正方形,
∴CG=CE,∠GCE=∠BCG=90°,∠GEF=45°,
∵∠FED<∠GEF,
∴∠FED<45°,故③错误,
∵CG=CE,∠GCE=∠BCG=90°,BC=CD,
∴△BCG≌△DCE(SAS),
∴∠GBC=∠CDE,
∵∠CDE+∠DEC=90°,
∴∠GBC+∠DEC=90°,
∴∠BHE=90°,
∴BH⊥DE,故④正确,
故答案为:①②④.
15.解:过点A作GH的平行线,交DC于点H′,交BE于点O',如图所示:
∵ABCD是正方形,
∴AG∥H′H,BA=AD,∠BAE=∠D=90°,
∴∠H′AD+∠AH′D=90°,
∵GH⊥BE,AH′∥GH,
∴AH′⊥BE,
∴∠H′AD+∠BEA=90°,
∴∠BEA=∠AH′D,
在△BAE和△ADH′中,,
∴△BAE≌△ADH′(AAS),
∴BE=AH′,
∵AG∥H′H,AH′∥GH,
∴四边形AH′HG是平行四边形,
∴GH=AH′,
∴GH=BE=6,
故答案为:6.
16.解:连接AC交BD于点O,如图所示:
∵四边形ABCD是矩形,
∴OA=OC=AC,OB=OD=BD,AC=BD,
∴OB=OC,
∴∠OBC=∠OCB,
∵CE=BD,
∴AC=CE,
∴∠CAE=∠E=15°,
∴∠OBC=∠OCB=∠CAE+∠E=30°,
∴∠AFB=∠OBC+∠E=30°+15°=45°;
故答案为:45°.
17.解:∵正方形ABCD,AC=4,
∴∠ACB=45°,BD⊥AC,OC==2,
∵EF⊥AC,EG⊥OB,
∴∠OFE=∠OGE=∠BOC=90°,
∴四边形GEFO为矩形,△CEF为等腰直角三角形,
∴EF=CF,EG=OF,
∴EF+EG=CF+OF=OC=2.
故答案为:2.
18.解:∵矩形ABCD,
∴OB=OD,
∵AE⊥BD于点E,OE=OD,
∴OE=OB,
∴△OAB是等腰三角形,
∴AB=OA=OB,
∴△OAB是等边三角形,
∴∠AOB=60°,
180°﹣60°=120°,
故答案为:60°或120°.
19.解:连接AP,
∵∠BAC=90°,PE⊥AB,PF⊥AC,
∴∠BAC=∠AEP=∠AFP=90°,
∴四边形AFPE是矩形,
∴EF=AP,
要使EF最小,只要AP最小即可,
当AP⊥BC时,AP最小,
在Rt△BAC中,∠BAC=90°,AB=6,BC=10,
由勾股定理得:AC===8,
由三角形面积公式得:△ABC的面积=×AB×AC=×BC×AP,
∴AP===4.8,
即EF=4.8,
故答案为:4.8.
20.解:(1)∵AD∥BC,AE∥DC,
∴四边形AECD为平行四边形,
∴AD=EC,
∵BC=2AD,
∴BC=2EC.
∴E为BC的中点
∵∠BAC=90°,
∴BC=2AE
∴AE=EC,
∵四边形AECD为平行四边形,
∴四边形AECD为菱形;
(2)解:连接DE,
∵AB=AE=2,AE=BE,
∴AB=AE=BE=2,
∴△ABE是等边三角形.
∴∠B=60°.
∵AD=BE,AD∥BC,
∴四边形ABED为平行四边形.
∴DE=AB=2,
∵∠B=60°,∠BAC=90°,AB=2,
∴BC=4.
∴.
∴SAECD==2.
21.(1)证明:∵点D是BC边的中点,点E是AD的中点,
∴DE是△BCF的中位线,
∴DE∥BF,
∴AD∥BF,
∵AF∥BC,
∴四边形AFBD是平行四边形;
(2)证明:(2)∵AB=AC,BD=DC,
∴AD⊥BC.
∴∠ADB=90°.
∵四边形AFBD是平行四边形,
∴四边形AFBD是矩形;
(3)当△ABC为等腰直角三角形,且∠BAC=90°时,四边形AFBD是正方形,理由如下:
∵四边形AFBD为平行四边形,
又∵等腰直角三角形ABC,且D为BC的中点,
∴AD=BD,∠ABD=90°,
∴四边形AFBD为正方形.
故答案为:∠BAC=90°.
22.证明:(1)连接GC,
∵四边形ABCD是正方形,
∴AB=BC,∠ABC=90°,∠ABD=∠CBD=45°,
又∵BG=BG,
∴△ABG≌△CBG(SAS),
∴AG=CG,∠BAG=∠BCG,
∵∠ABC+∠BAG+∠AGF+∠BFG=360°,且∠ABC=∠AGF=90°,
∴∠BAG+∠BFG=180°,
∴∠BCG+∠BFG=180°,
∵∠BFG+∠GFC=180°,
∴∠BCG=∠GFC,
∴GC=GF,
∴AG=FG;
(2)如图2,过点G作GH⊥BC于H,
∵AB=10,BF=4,
∴AF2=AB2+BF2=AG2+GF2,
∴GF2=58,
∵∠DBC=45°,GH⊥BC,
∴BH=GH,BG=GH,
∵GF2=GH2+FH2,
∴58=GH2+(GH﹣4)2,
∴GH=7,(负值舍去),
∴BG=7;
(3)如图,在AB上截取BF=BN,连接NF,
∵AG=GF,AG⊥GF,
∴∠EAF=45°,
∵AE=AF,AB=AD,
∴Rt△ABF≌Rt△ADE(HL),
∴∠BAF=∠DAE=22.5°,BF=DE,
∴CF=CE,
∵BF=BN,∠ABC=90°,
∴NF=BF,∠BNF=∠BFN=45°,
∴∠BAF=∠AFN=22.5°,
∴AN=NF=BF,
∵AB=BC,
∴BN+AN=BF+FC,
∴FC=BF,
∴BC=(+1)BF,
∴正方形ABCD与△CEF的面积之比=BC2:FC2=3+2:1.
23.(1)证明:∵四边形ABCD是平行四边形,
又∵AC⊥BD,
∴四边形ABCD是菱形.
∴BC=CD.
又∵CE=BC,
∴BE=2BC,
∴BE=2CD;
(2)证明:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BE,
又∵CE=BC,
∴AD=CE,AD∥CE,
∴四边形ACED是平行四边形.
∵∠ACB=90°,
∴平行四边形ACED是矩形,
又∵CA=CB,
∴CA=CE,
∴矩形ACED是正方形.
24.(1)证明:∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵点E、点F分别是OB、OD的中点,
∴OE=OB,OF=OD,
∴OE=OF,
∴四边形AECF是平行四边形,
∵AC⊥AB,∠AOB=60°,
∴∠ABO=30°,
∴OA=OB=OE,
∴AC=EF,
∴四边形AECF为矩形;
(2)解:由(1)得:OA=OE=OC=OF,∠AOB=60°,∠ABO=30°,
∴△OAE是等边三角形,∠OFA=∠OAF=30°=∠ABO,
∴AE=OA,AF=AB=3,
∵AC⊥AB,
∴∠OAB=90°,
∴AE=OA=AB=,
∴矩形AECF的面积=AF×AE=3.
25.(1)解:BE+DF=EF;理由如下:
如图1,延长FD到G,使DG=BE,连接AG,
∵在△GDA和△EBA中,
,
∴△GDA≌△EBA(SAS),
∴AG=AE,∠GAD=∠EAB,
故∠GAF=45°,
在△GAF和△EAF中,
∵,
∴△GAF≌△EAF(SAS),
∴GF=EF,
即GD+DF=BE+DF=EF;
(2)AH=AB,理由如下:
∵四边形ABCD为正方形,
∴AB=AD,∠BAD=90°,
∴把△ADF绕点A顺时针旋转90°得到△ABQ,如图2,
∴AQ=AF,∠FAQ=90°,∠ABQ=∠D=90°,
而∠ABC=90°,
∴点Q在CB的延长线上,
∵∠EAF=45°,
∴∠QAE=90°﹣∠EAF=45°,
∴∠EAF=∠QAE,
在△AEQ和△AEF中,
,
∴△AEQ≌△AEF(SAS),
∴EQ=EF,
∵AB⊥EQ,AH⊥FE,
∴AB=AH.
26.解:(1)∵四边形ABCD是正方形,
∴∠DBC=∠ABG=45°,AB=BC=CD=2,
∵GF⊥BC,
∴∠GBF=45°=∠BGF,
∵∠AGF=105°,
∴∠AGB=60°,
∵∠AGB+∠BAG+∠ABG=180°,
∴∠BAG=180°﹣45°﹣60°=75°;
(2)如图,连接CG,过点A作AH⊥BD于点H,
∵四边形ABCD是正方形,
∴A、C关于对角线BD对称,
∵点G在BD上,
∴GA=GC,
∵GE⊥DC于点E,GF⊥BC于点F,
∴∠GEC=∠ECF=∠CFG=90°,
∴四边形EGFC是矩形,
∴EF=GC,
∴AG=EF,
∵AB=2,∠ABH=45°,AH⊥BG,
∴BH=AH=,
∵∠AGB=60°,AH⊥BG,AH=,
∴,AG=2HG=,
∴EF=.
27.解:(1)∵四边形ABCD是正方形,
∴AD=AB=2,BD=AD=2,∠ABD=∠CBD=45°,
∴BE=BD﹣DE=2﹣1,
∵EG⊥BD,∠DBG=45°,
∴∠DBG=∠EGB=45°,
∴EB=EG=2﹣1;
(2)∵AE⊥EF,
∴∠AEF=∠BEG=90°,
∴∠AEB=∠GEF,
又∵BE=EG,∠ABD=∠FGE=45°,
∴△ABE≌△FGE(AAS),
∴FG=AB.
28.(1)证明:∵AB⊥BC,CD⊥BC,
∴AB∥CD,
∵AB=CD,
∴四边形ABCD是平行四边形,
∵AB⊥BC,
∴∠ABC=90°,
∴四边形ABCD为矩形;
(2)解:∵四边形ABCD为矩形,
∴∠BAC=90°,
∵AB=3,AD=4,
∴BD=5,
∵S△ABD=AB?AD=BD?AE,
∴3×4=5AE,
∴AE=,
∵AC=BD=5,
∴AO=AC=,
∵AE⊥BD,
∴OE===,
∴△AEO的面积==.
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
