5.1矩形-2020-2021学年浙教版八年级数学下册同步提升训练(Word版 含解析)
文档属性
| 名称 | 5.1矩形-2020-2021学年浙教版八年级数学下册同步提升训练(Word版 含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 396.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-04 10:03:06 | ||
图片预览

文档简介
2020-2021年度浙教版八年级数学下册《5.1矩形》同步提升训练(附答案)
1.在四边形ABCD中,AD∥BC,下列选项中,不能判定四边形ABCD为矩形的是( )
A.AD=BC且AC=BD B.AD=BC且∠A=∠B
C.AB=CD且∠A=∠C D.AB=CD且∠A=∠B
2.如图,矩形ABCD中,对角线AC,BD相交于点O,若∠OAD=40°,则∠COD=( )
A.20° B.40° C.80° D.100°
3.已知矩形ABCD,一条直线将该矩形分割成两个多边形,则所得任一多边形的内角和度数不可能是( )
A.180° B.360° C.540° D.720°
4.如图,矩形ABCD中,点E在BC上,且AE平分∠BAC,AE=CE,BE=2,则矩形ABCD的面积为( )
A.24 B.24 C.12 D.12
5.如图,长方形ABCD中,AD=BC=6,AB=CD=10.点E为射线DC上的一个动点,△ADE与△AD′E关于直线AE对称,当△AD′B为直角三角形时,DE的长为( )
A.2或8 B.或18 C.或2 D.2或18
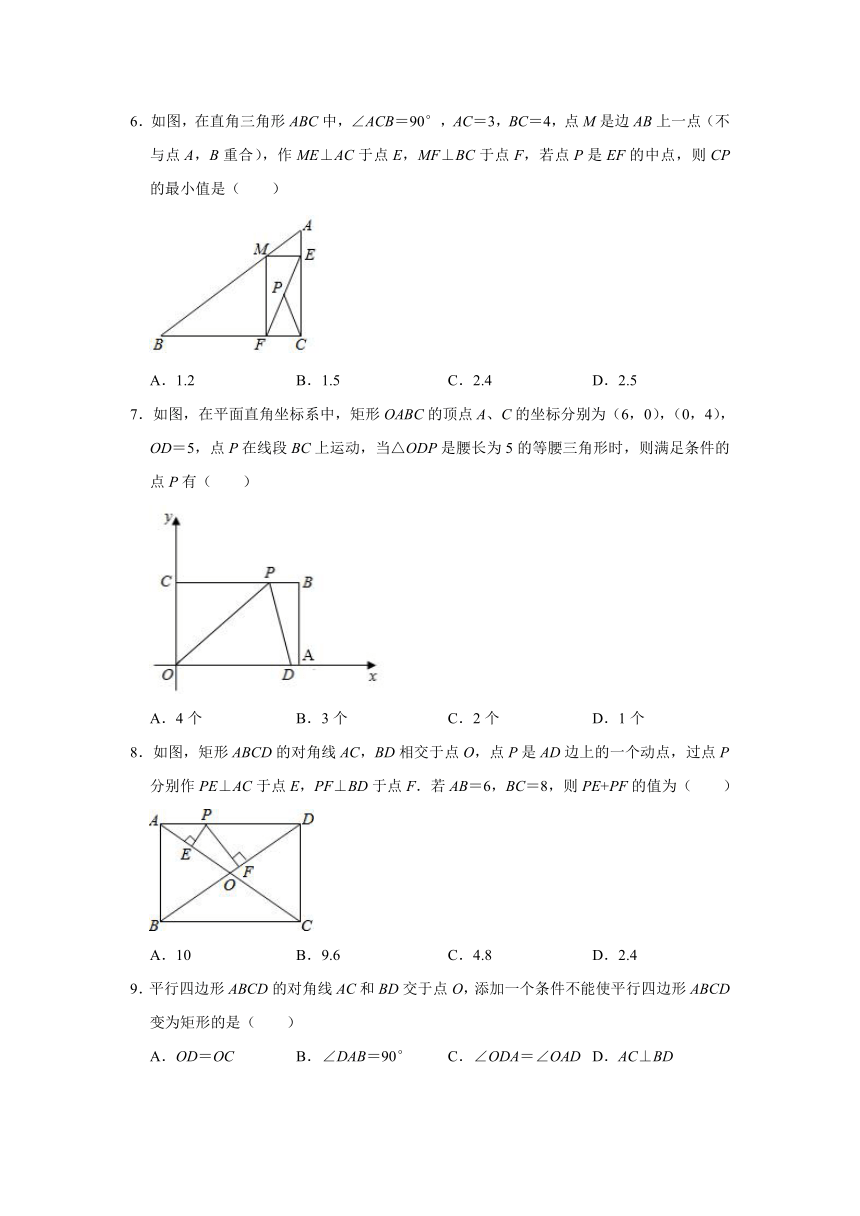
6.如图,在直角三角形ABC中,∠ACB=90°,AC=3,BC=4,点M是边AB上一点(不与点A,B重合),作ME⊥AC于点E,MF⊥BC于点F,若点P是EF的中点,则CP的最小值是( )
A.1.2 B.1.5 C.2.4 D.2.5
7.如图,在平面直角坐标系中,矩形OABC的顶点A、C的坐标分别为(6,0),(0,4),OD=5,点P在线段BC上运动,当△ODP是腰长为5的等腰三角形时,则满足条件的点P有( )
A.4个 B.3个 C.2个 D.1个
8.如图,矩形ABCD的对角线AC,BD相交于点O,点P是AD边上的一个动点,过点P分别作PE⊥AC于点E,PF⊥BD于点F.若AB=6,BC=8,则PE+PF的值为( )
A.10 B.9.6 C.4.8 D.2.4
9.平行四边形ABCD的对角线AC和BD交于点O,添加一个条件不能使平行四边形ABCD变为矩形的是( )
A.OD=OC B.∠DAB=90° C.∠ODA=∠OAD D.AC⊥BD
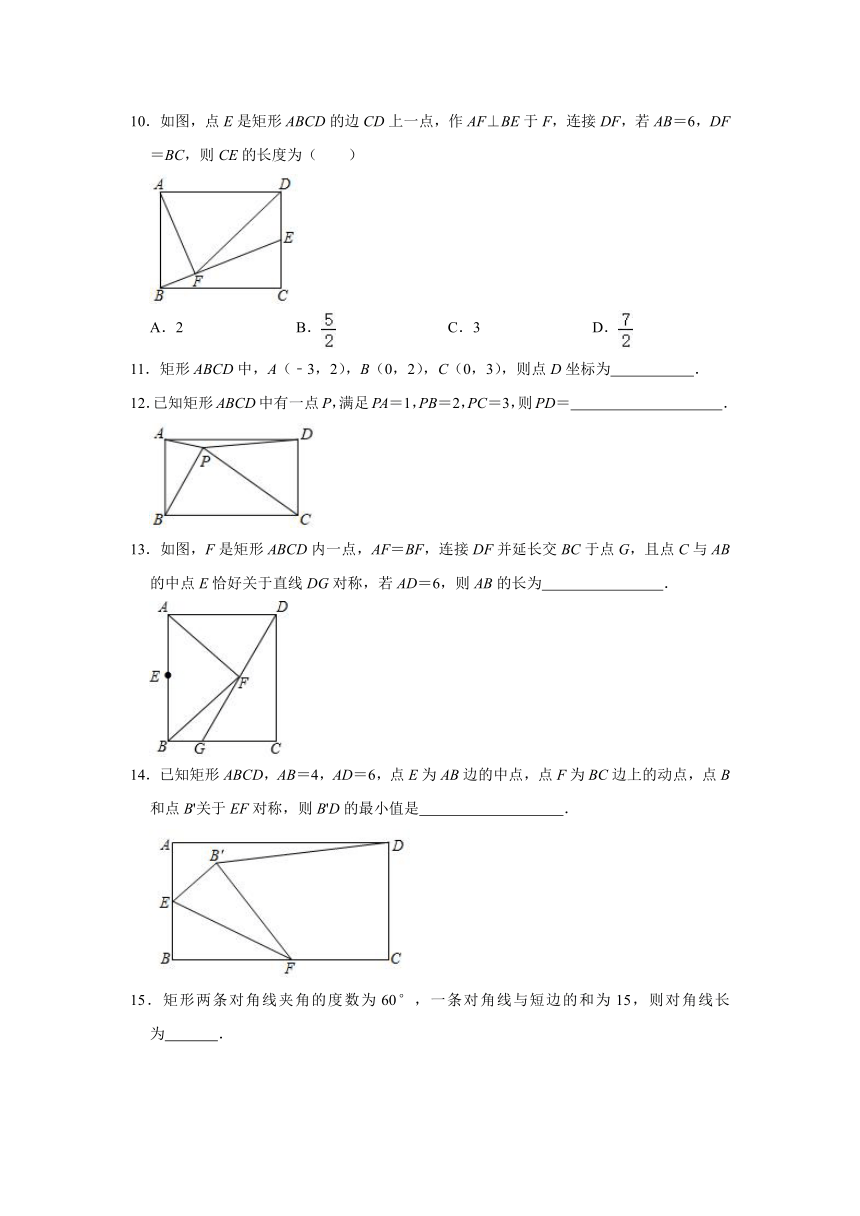
10.如图,点E是矩形ABCD的边CD上一点,作AF⊥BE于F,连接DF,若AB=6,DF=BC,则CE的长度为( )
A.2 B. C.3 D.
11.矩形ABCD中,A(﹣3,2),B(0,2),C(0,3),则点D坐标为 .
12.已知矩形ABCD中有一点P,满足PA=1,PB=2,PC=3,则PD= .
13.如图,F是矩形ABCD内一点,AF=BF,连接DF并延长交BC于点G,且点C与AB的中点E恰好关于直线DG对称,若AD=6,则AB的长为 .
14.已知矩形ABCD,AB=4,AD=6,点E为AB边的中点,点F为BC边上的动点,点B和点B'关于EF对称,则B'D的最小值是 .
15.矩形两条对角线夹角的度数为60°,一条对角线与短边的和为15,则对角线长为 .
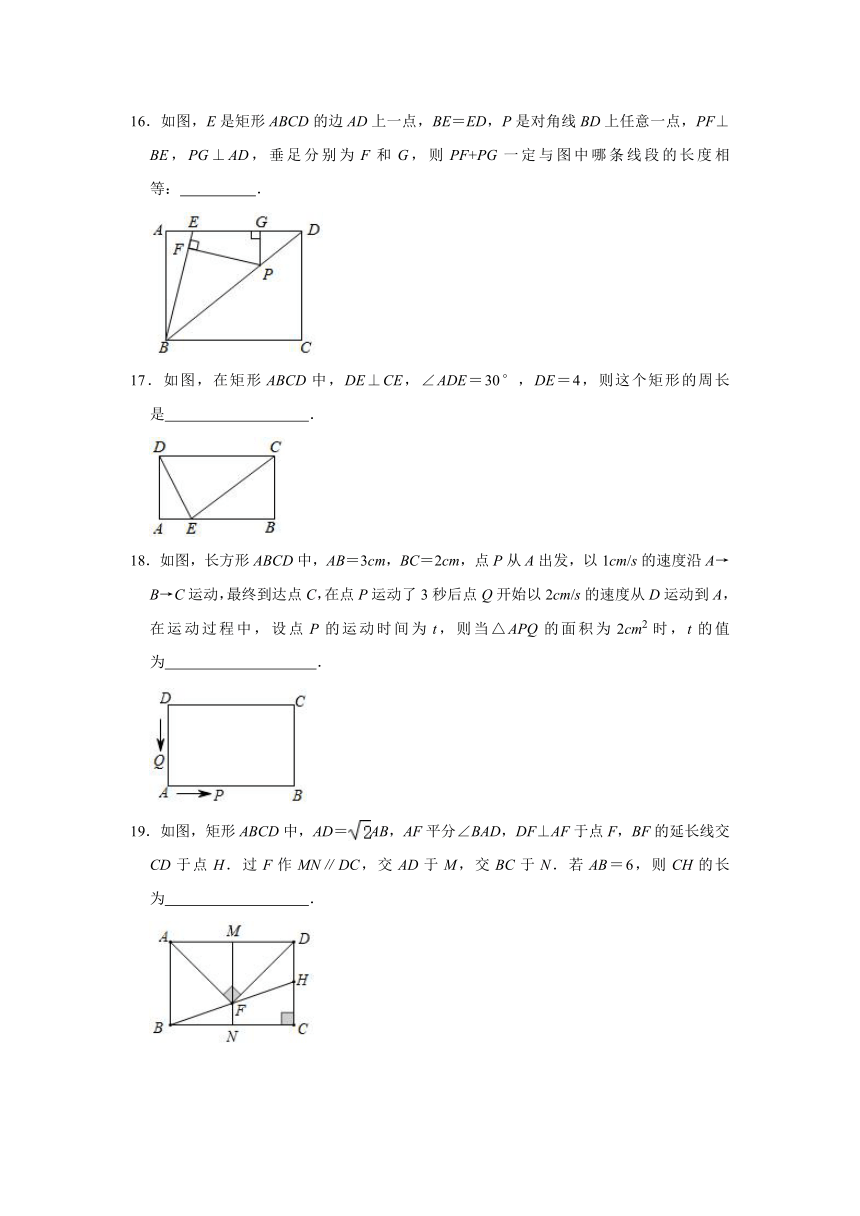
16.如图,E是矩形ABCD的边AD上一点,BE=ED,P是对角线BD上任意一点,PF⊥BE,PG⊥AD,垂足分别为F和G,则PF+PG一定与图中哪条线段的长度相等: .
17.如图,在矩形ABCD中,DE⊥CE,∠ADE=30°,DE=4,则这个矩形的周长是 .
18.如图,长方形ABCD中,AB=3cm,BC=2cm,点P从A出发,以1cm/s的速度沿A→B→C运动,最终到达点C,在点P运动了3秒后点Q开始以2cm/s的速度从D运动到A,在运动过程中,设点P的运动时间为t,则当△APQ的面积为2cm2时,t的值为 .
19.如图,矩形ABCD中,AD=AB,AF平分∠BAD,DF⊥AF于点F,BF的延长线交CD于点H.过F作MN∥DC,交AD于M,交BC于N.若AB=6,则CH的长为 .
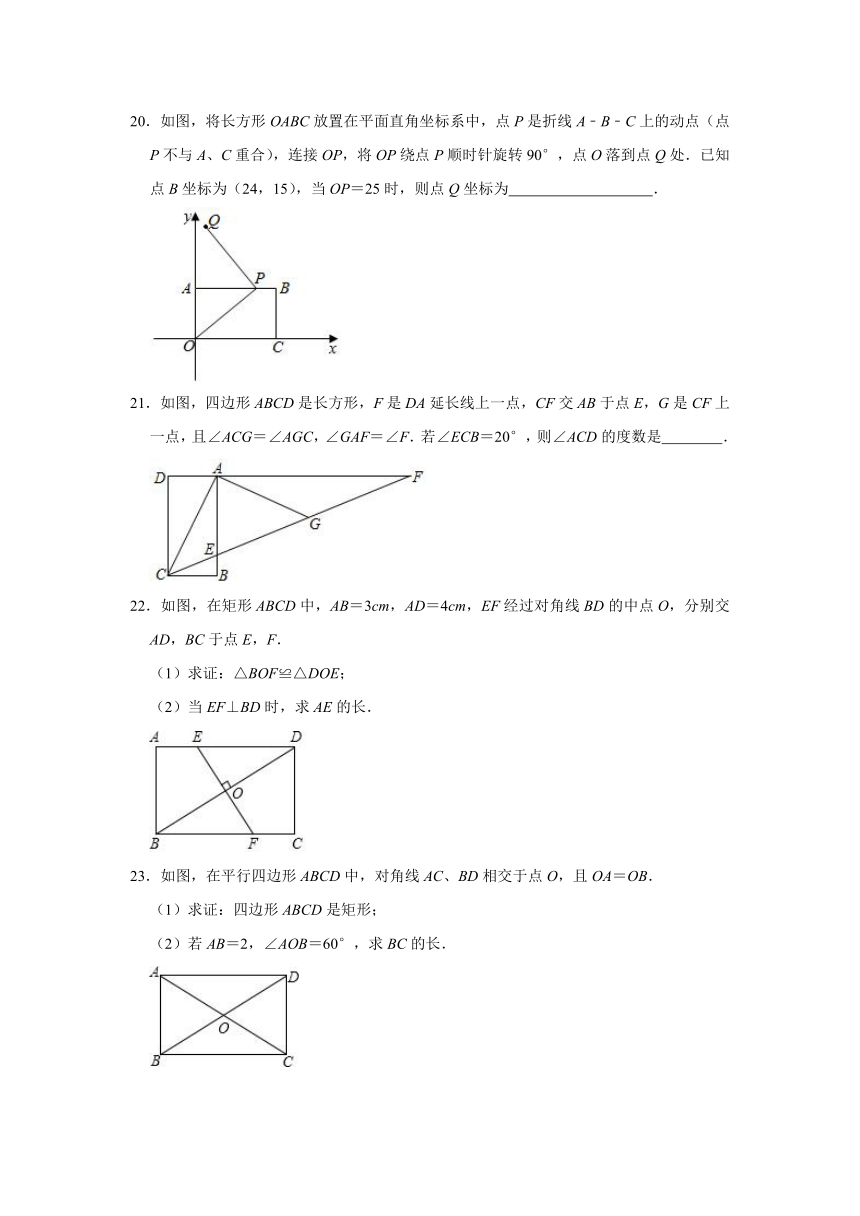
20.如图,将长方形OABC放置在平面直角坐标系中,点P是折线A﹣B﹣C上的动点(点P不与A、C重合),连接OP,将OP绕点P顺时针旋转90°,点O落到点Q处.已知点B坐标为(24,15),当OP=25时,则点Q坐标为 .
21.如图,四边形ABCD是长方形,F是DA延长线上一点,CF交AB于点E,G是CF上一点,且∠ACG=∠AGC,∠GAF=∠F.若∠ECB=20°,则∠ACD的度数是 .
22.如图,在矩形ABCD中,AB=3cm,AD=4cm,EF经过对角线BD的中点O,分别交AD,BC于点E,F.
(1)求证:△BOF≌△DOE;
(2)当EF⊥BD时,求AE的长.
23.如图,在平行四边形ABCD中,对角线AC、BD相交于点O,且OA=OB.
(1)求证:四边形ABCD是矩形;
(2)若AB=2,∠AOB=60°,求BC的长.
24.如图,矩形ABCD的对角线AC,BD交于点O,以OC,OD为邻边作平行四边形OCED,连接OE.
(1)求证:四边形OBCE是平行四边形;
(2)连接BE交AC于点F.若AB=2,∠AOB=60°,求BF的长.
25.如图,在四边形ABCD中,AD∥BC,AD≠BC,AB∥DE,AF∥DC,E、F两点在BC边上,且BC=3AD.
(1)求证:四边形AEFD是平行四边形.
(2)当AB=DC时,求证:平行四边形AEFD是矩形.
26.如图,在矩形ABCD中,对角线AC、BD交于点O,BE平分∠ABC交AC于点F,交AD于点E,且∠DBF=15°,
求证:(1)AO=AE;
(2)∠FEO的度数.
27.如图,矩形ABCD的对角线AC,BD相交于点O,过点B作AC的平行线交DC的延长线于点E.
(1)求证:BD=BE;
(2)连接OE,若AB=4,BC=6,求OE的长.
参考答案
1.解:A、∵AD∥BC,AD=BC,
∴四边形ABCD是平行四边形,
∵AC=BD,
∴平行四边形ABCD是矩形,故选项A不符合题意;
B、∵AD∥BC,AD=BC,
∴四边形ABCD是平行四边形,∠A+∠B=180°,
∵∠A=∠B,
∴∠A=∠B=90°,
∴平行四边形ABCD是矩形,故选项B不符合题意;
C、∵AD∥BC,
∴∠A+∠B=∠C+∠D=180°,
∵∠A=∠C,
∴∠B=∠D,
∴四边形ABCD是平行四边形,AB=CD,故选项C不符合题意;
D、∵AD∥BC,
∴∠A+∠B=180°,
∵∠A=∠B,
∴∠A=∠B=90°,
∴AB⊥AD,AB⊥BC,AB的长为AD、BC间的距离,
又∵AB=CD,
∴CD⊥AD,
∴∠ADC=90°,
∴四边形ABCD是矩形,
∴选项D不符合题意;
故选:C.
2.解:∵矩形ABCD中,对角线AC,BD相交于点O,
∴OD=OB=OA=OC,
∵∠OAD=40°,
∴∠ODA=∠OAD=40°,
∴∠COD=∠ODA+∠OAD=40°﹣40°=80°,
故选:C.
3.解:不同的划分方法有4种,见图:
所得任一多边形内角和度数可能是360°或540°或180°.
故选:D.
4.解:∵四边形ABCD是矩形,
∴∠B=90°,
∴∠BAC+∠BCA=90°,
∵AE平分∠BAC,AE=CE,
∴∠BAE=∠EAC=∠ECA,
∴∠BAE+∠EAC+∠ECA=90°,
∴∠BAE=∠EAC=∠ECA=30°,
∴AE=CE=2BE=4,AB=2,
∴BC=BE+CE=6,
∴矩形ABCD面积=AB×BC=2×6=12;
故选:C.
5.解:分两种情况讨论:
①当E点在线段DC上时,
∵△AD'E≌△ADE,
∴∠AD'E=∠D=90°,
∵∠AD'B=90°,
∴∠AD'B+∠AD'E=180°,
∴B、D'、E三点共线,
∵,AD'=AD,
∴BE=AB=10,
∵,
∴DE=D'E=10﹣8=2;
②当E点在线段DC的延长线上时,如下图,
∵∠ABD″+∠CBE=∠ABD″+∠BAD″=90°,
∴∠CBE=∠BAD″,
在△ABD″和△BEC中,
∵,
∴△ABD″≌△BEC(ASA),
∴BE=AB=10,
∵,
∴DE=D″E=BD''+BE=8+10=18.
综上所知,DE=2或18.
故选:D.
6.解:连接CM,如图所示:
∵∠ACB=90°,AC=3,BC=4,
∴AB===5,
∵ME⊥AC,MF⊥BC,∠ACB=90°,
∴四边形CEMF是矩形,
∴EF=CM,
∵点P是EF的中点,
∴CP=EF,
当CM⊥AB时,CM最短,
此时EF也最小,则CP最小,
∵△ABC的面积=AB×CM=AC×BC,
∴CM===2.4,
∴CP=EF=CM=1.2,
故选:A.
7.解:由题意,当△ODP是腰长为5的等腰三角形时,有三种情况:
(1)如答图①所示,PD=OD=5,点P在点D的左侧.
过点P作PE⊥x轴于点E,则PE=4.
在Rt△PDE中,由勾股定理得:DE===3,
∴OE=OD﹣DE=5﹣3=2,
∴此时点P坐标为(2,4);
(2)如答图②所示,OP=OD=5.
过点P作PE⊥x轴于点E,则PE=4.
在Rt△POE中,由勾股定理得:OE===3,
∴此时点P坐标为(3,4);
(3)如答图③所示,PD=OD=5,点P在点D的右侧.
过点P作PE⊥x轴于点E,则PE=4.
在Rt△PDE中,由勾股定理得:DE===3,
∴OE=OD+DE=5+3=8,
∴此时点P坐标为(8,4)(舍弃).
综上所述,点P的坐标为:(2,4)或(3,4);
故选:C.
8.解:连接OP,
∵矩形ABCD的两边AB=6,BC=8,
∴S矩形ABCD=AB?BC=48,OA=OC,OB=OD,AC=BD,AC==10,
∴S△AOD=S矩形ABCD=12,OA=OD=5,
∴S△AOD=S△AOP+S△DOP=OA?PE+OD?PF=OA(PE+PF)=×5×(PE+PF)=12,
∴PE+PF==4.8.
故选:C.
9.解:∵四边形ABCD是平行四边形,
∴OA=OC=AC,OB=OD=BD,
A、OD=OC时,AC=BD,
∴平行四边形ABCD是矩形,故选项A不符合题意;
B、四边形ABCD是平行四边形,∠DAB=90°,
∴平行四边形ABCD是矩形,故选项B不符合题意;
C、∵∠ODA=∠OAD,
∴OA=OD,
∴AC=BD,
∴平行四边形ABCD是矩形,故选项C不符合题意;
D、四边形ABCD是平行四边形,AC⊥BD,
∴平行四边形ABCD是菱形,故选项D符合题意;
故选:D.
10.解:过D作DH⊥AF于点H,延长DH与AB相交于点G,
∵四边形ABCD为矩形,
∴AD=BC,
∵DF=BC,
∴DA=DF,
∴AH=FH,
∵AF⊥BE,
∴DG∥BE,
∴AG=BG=,
∵矩形ABCD中,AB=DC=6,AB∥DC,
∴四边形BEDG为平行四边形,
∴DE=BG=3,
∴CE=CD﹣DE=6﹣3=3.
故选:C.
11.解:在矩形ABCD中A(﹣3,2),C(0,4),B(0,2).
∴点D的横坐标为﹣3,纵坐标为4.
∴点D的坐标为(﹣3,4).
故答案为:(﹣3,4).
12.解:过点P作GH∥BC交AB、CD于点G、H,
过P作EF∥AB交AD、BC于点E、F,
设AE=BF=c,AG=DH=a,
GB=HC=b,ED=FC=d,
∴AP2=a2+c2,
CP2=b2+d2,
BP2=b2+c2,
DP2=d2+a2,
∵AP=1,BP=2,CP=3,
∴AP2+CP2=BP2+DP2,
1+9=4+DP2,
DP2=6,
DP=.
故答案为:.
13.解:连接EF、EG、EC,如图所示:
∵四边形ABCD是矩形,
∴BC=AD=6,AD∥BC,∠BAD=∠ABC=90°,
∴AB⊥AD,
∵AF=BF,点E是AB的中点,
∴EF⊥AB,
∴EF∥AD∥BC,
∴EF是梯形ABGD的中位线,∠EFG=∠CGF,
∴EF=(AD+BG),
设BG=x,则CG=6﹣x,EF=(6+x),
∵点C与AB的中点E关于直线DG对称,
∴EG=CG,∠CGF=∠EGF,
∴∠EFG=∠EGF,
∴EG=EF,
∴EF=CG,
∴(6+x)=6﹣x,
解得:x=2,
∴BG=2,EG=CG=4,
∴BE===2.
∴AB=2BE=4;
故答案为:4.
14.解:∵四边形ABCD是矩形,AB=4,AD=6,点E为AB边的中点,点B和点B'关于EF对称,
∴AE=BE=B'E=2,∠A=90°,
∴DE==2,
∴当点B'在线段DE上时,B'D取得最小值,此时B'D=2﹣2,
故答案为:2﹣2.
15.解:∵四边形ABCD是矩形,
∴OA=OC,OB=OD,AC=BD,
∴OA=OB,
∵∠AOB=60°,
∴△OAB是等边三角形,
∴AB=OB=OA=×15=5,
∴AC=BD=2×5=10.
故答案为:10.
16.证明:连接PE,如图
∵BE=ED,PF⊥BE,PG⊥AD,
∴S△BDE=S△BEP+S△DEP==,
又∵四边形ABCD是矩形,
∴BA⊥AD,AB=CD,
∴S△BED=,
∴,
∴PF+PG=AB=CD.
故答案为:AB或CD.
17.解:∵四边形ABCD是矩形,
∴∠A=∠B=90°,AD=BC.
在Rt△ADE中,
∵∠A=90°,∠ADE=30°,DE=4,
∴AE=DE=2,AD=AE=2.
∵DE⊥CE,∠A=90°,
∴∠BEC=∠ADE=90°﹣∠AED=30°.
在Rt△BEC中,
∵∠B=90°,∠BEC=30°,BC=AD=2,
∴BE=BC=6,
∴AB=AE+BE=2+6=8,
∴矩形ABCD的周长=2(AB+AD)=2(8+2)=16+4.
故答案为:16+4.
18.解:∵四边形ABCD是矩形,
∴∠BAD=90°,AD=BC=2cm,
分两种情况:
①点P在AB上时,点Q在D处,如图1所示:
∵△APQ的面积为2cm2,
∴×t×2=2,
解得:t=2;
②点P在BC上时,如图2所示:
∵△APQ的面积为2cm2,
∴×AQ×3=2,
解得:AQ=,
∴DQ=AD﹣AQ=2﹣==2(t﹣3),
解得:t=;
综上所述,当△APQ的面积为2cm2时,t的值为2或;
故答案为:2或.
19.解:根据题意可知:
MN=CD,
∵四边形ABCD是矩形,
∴∠BAD=90°,DC⊥AD,CD=AB=6,
∴MF⊥AD,MN=6,
∵AF平分∠BAD,
∴∠BAF=∠DAF=45°,
∵AB=6,
∴AD=AB=6,
∵DF⊥AF,
∴△ADF是等腰直角三角形,
∴AF=DF,
∴点M是AD的中点,
∴FM=AD=3,FN为△BCH的中位线,
∴FN=MN﹣FM=6﹣3,FN=CH,
∴CH=2FN=12﹣6.
故答案为:12﹣6.
20.解:如图1,当点P在AB上,过点Q作QE⊥AB于E,
∵点B坐标为(24,15),
∴AB=OC=24,AO=BC=15,
∴AP===20,
∵将OP绕点P顺时针旋转90°,
∴OP=PQ,∠OPQ=90°,
∴∠QPE+∠OPA=90°=∠APO+∠AOP,
∴∠QPE=∠AOP,
在△EPQ和△AOP中,
,
∴△EPQ≌△AOP(AAS),
∴EP=AO=15,QE=AP=20,
∴AE=AP﹣EP=5,
∴点Q(5,35);
当点P在BC上时,过点Q作QF⊥BC,交CB的延长线于F,
∴CP===7,
∵将OP绕点P顺时针旋转90°,
∴OP=PQ,∠OPQ=90°,
∴∠QPF+∠OPC=90°,∠OPC+∠POC=90°,
∴∠POC=∠QPF,
在△OPC和△PQF中,
,
∴△OPC≌△PQF(AAS),
∴QF=CP=7,PF=OC=24,
∴CF=31,
∴点Q(17,31),
综上所述:点Q坐标为:(5,35)或(17,31),
故答案为:(5,35)或(17,31).
21.解:∵四边形ABCD是矩形,
∴AD∥BC,∠DCB=90°,
∴∠F=∠ECB=20°,
∴∠GAF=∠F=20°,
∴∠ACG=∠AGC=∠GAF+∠F=2∠F=40°,
∴∠ACB=∠ACG+∠ECB=60°,
∴∠ACD=90°﹣60°=30°,
故答案为:30°.
22.(1)证明:∵四边形ABCD是矩形,
∴AD∥BC,
∴∠BFO=∠DEO,∠FBO=∠EDO,
又∵O是BD中点,
∴OB=OD,
∴△BOF≌△DOE(ASA).
(2)连接BE.
∵EF⊥BD,O为BD中点,
∴EB=ED,
设AE=xcm,由EB=ED=AD﹣AE=(4﹣x)cm,
在Rt△ABE中,AB=3cm,
根据勾股定理得:AB2+AE=BE2,即9+x2=(4﹣x)2,
解得:x=,
∴AE的长是 cm.
23.解:(1)证明:∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD
又∵OA=OB
∴OA=OB=OC=OD
∴AC=BD
∴四边形ABCD是矩形
证法二:
∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD
又∵OA=OB
∴△ABD是以∠BAD为直角的直角三角形,
∴∠BAD=90°
根据矩形的定义知,四边形ABCD是矩形.
(2)∵OA=OB,∠AOB=60°
∴△AOB是等边三角形,
∴OA=OB=AB=2
∴AC=2OA=4
∴在Rt△ABC中,根据勾股定理,有AB2+BC2=AC2
∴BC2=AC2﹣AB2=42﹣22=16﹣4=12
∴BC=
24.(1)证明:∵四边形ABCD是矩形,
∴OA=OB=OC=OD,
∵四边形OCED是平行四边形,
∴四边形OCED为菱形,
∴CE∥OB,CE=OB,
∴四边形OBCE为平行四边形;
(2)解:过F作FM⊥BC于M,过O作ON⊥BC于N,
∵FM⊥BC,ON⊥BC,
∴ON∥FM,
∵AO=OC,
∴ON=AB=1,
∵OF=FC,
∴FM=ON=,
∵∠AOB=60°,OA=OB,
∴∠OAB=60°,∠ACB=30°,
在 Rt△ABC中:
∵AB=2,∠ACB=30°,
∴BC=2,
∵∠ACB=30°,FM=,
∴CM=,
∴BM=BC﹣CM=,
∴BF==.
25.(1)证明:∵AD∥BC,AB∥DE,AF∥DC,
∴四边形ABED和四边形AFCD都是平行四边形.
∵AD=BE,AD=FC,
∵BC=BE+EF+FC=3AD,
∴AD=EF,
∴四边形AEFD是平行四边形;
(2)证明:∵四边形ABED和四边形AFCD都是平行四边形,
∴DE=AB,AF=DC.
∵AB=DC,
∴DE=AF.
又∵四边形AEFD是平行四边形,
∴四边形AEFD是矩形.
26.证明:(1)∵四边形ABCD是矩形,
∴∠BAD=∠ABC=90°,AC=BD,AO=OC,BO=OD,
∴OA=OB,
∵BE平分∠ABC,
∴∠ABE=45°,△ABE为等腰直角三角形,
∴AB=AE.
又∵∠DBF=15°,
∴∠ABO=60°,
∵OA=OB,
∴△AOB是等边三角形,
∴AO=AB,
又∵AB=AE.
∴AO=AE.
(2)由(1)知:△AOB是等边三角形,
∴∠BAO=60°,
∴∠OAE=30°,
又∵AO=AE
∴∠AEO=∠AOE=75°,
∵∠BAE=90°,∠AEB=45°,
∴∠FEO=30°.
27.(1)证明:∵四边形ABCD是矩形,
∴AC=BD,AB∥CD,
又∵BE∥AC,
∴四边形ABEC是平行四边形,
∴AC=BE,
∴BD=BE;
(2)如图,过点O作OF⊥CD于点F,
∵四边形ABCD是矩形,
∴点O是BD的中点,即OB=OD,
∴OF为△BCD的中位线,
∴OF=BC=3,
又∵四边形ABEC是平行四边形,
∴∠BCD=90°,AB=CE=DC=4.
∴CF=DF=CD=2,
∴EF=6.
在直角△OEF中,由勾股定理可得:OE===3.
1.在四边形ABCD中,AD∥BC,下列选项中,不能判定四边形ABCD为矩形的是( )
A.AD=BC且AC=BD B.AD=BC且∠A=∠B
C.AB=CD且∠A=∠C D.AB=CD且∠A=∠B
2.如图,矩形ABCD中,对角线AC,BD相交于点O,若∠OAD=40°,则∠COD=( )
A.20° B.40° C.80° D.100°
3.已知矩形ABCD,一条直线将该矩形分割成两个多边形,则所得任一多边形的内角和度数不可能是( )
A.180° B.360° C.540° D.720°
4.如图,矩形ABCD中,点E在BC上,且AE平分∠BAC,AE=CE,BE=2,则矩形ABCD的面积为( )
A.24 B.24 C.12 D.12
5.如图,长方形ABCD中,AD=BC=6,AB=CD=10.点E为射线DC上的一个动点,△ADE与△AD′E关于直线AE对称,当△AD′B为直角三角形时,DE的长为( )
A.2或8 B.或18 C.或2 D.2或18
6.如图,在直角三角形ABC中,∠ACB=90°,AC=3,BC=4,点M是边AB上一点(不与点A,B重合),作ME⊥AC于点E,MF⊥BC于点F,若点P是EF的中点,则CP的最小值是( )
A.1.2 B.1.5 C.2.4 D.2.5
7.如图,在平面直角坐标系中,矩形OABC的顶点A、C的坐标分别为(6,0),(0,4),OD=5,点P在线段BC上运动,当△ODP是腰长为5的等腰三角形时,则满足条件的点P有( )
A.4个 B.3个 C.2个 D.1个
8.如图,矩形ABCD的对角线AC,BD相交于点O,点P是AD边上的一个动点,过点P分别作PE⊥AC于点E,PF⊥BD于点F.若AB=6,BC=8,则PE+PF的值为( )
A.10 B.9.6 C.4.8 D.2.4
9.平行四边形ABCD的对角线AC和BD交于点O,添加一个条件不能使平行四边形ABCD变为矩形的是( )
A.OD=OC B.∠DAB=90° C.∠ODA=∠OAD D.AC⊥BD
10.如图,点E是矩形ABCD的边CD上一点,作AF⊥BE于F,连接DF,若AB=6,DF=BC,则CE的长度为( )
A.2 B. C.3 D.
11.矩形ABCD中,A(﹣3,2),B(0,2),C(0,3),则点D坐标为 .
12.已知矩形ABCD中有一点P,满足PA=1,PB=2,PC=3,则PD= .
13.如图,F是矩形ABCD内一点,AF=BF,连接DF并延长交BC于点G,且点C与AB的中点E恰好关于直线DG对称,若AD=6,则AB的长为 .
14.已知矩形ABCD,AB=4,AD=6,点E为AB边的中点,点F为BC边上的动点,点B和点B'关于EF对称,则B'D的最小值是 .
15.矩形两条对角线夹角的度数为60°,一条对角线与短边的和为15,则对角线长为 .
16.如图,E是矩形ABCD的边AD上一点,BE=ED,P是对角线BD上任意一点,PF⊥BE,PG⊥AD,垂足分别为F和G,则PF+PG一定与图中哪条线段的长度相等: .
17.如图,在矩形ABCD中,DE⊥CE,∠ADE=30°,DE=4,则这个矩形的周长是 .
18.如图,长方形ABCD中,AB=3cm,BC=2cm,点P从A出发,以1cm/s的速度沿A→B→C运动,最终到达点C,在点P运动了3秒后点Q开始以2cm/s的速度从D运动到A,在运动过程中,设点P的运动时间为t,则当△APQ的面积为2cm2时,t的值为 .
19.如图,矩形ABCD中,AD=AB,AF平分∠BAD,DF⊥AF于点F,BF的延长线交CD于点H.过F作MN∥DC,交AD于M,交BC于N.若AB=6,则CH的长为 .
20.如图,将长方形OABC放置在平面直角坐标系中,点P是折线A﹣B﹣C上的动点(点P不与A、C重合),连接OP,将OP绕点P顺时针旋转90°,点O落到点Q处.已知点B坐标为(24,15),当OP=25时,则点Q坐标为 .
21.如图,四边形ABCD是长方形,F是DA延长线上一点,CF交AB于点E,G是CF上一点,且∠ACG=∠AGC,∠GAF=∠F.若∠ECB=20°,则∠ACD的度数是 .
22.如图,在矩形ABCD中,AB=3cm,AD=4cm,EF经过对角线BD的中点O,分别交AD,BC于点E,F.
(1)求证:△BOF≌△DOE;
(2)当EF⊥BD时,求AE的长.
23.如图,在平行四边形ABCD中,对角线AC、BD相交于点O,且OA=OB.
(1)求证:四边形ABCD是矩形;
(2)若AB=2,∠AOB=60°,求BC的长.
24.如图,矩形ABCD的对角线AC,BD交于点O,以OC,OD为邻边作平行四边形OCED,连接OE.
(1)求证:四边形OBCE是平行四边形;
(2)连接BE交AC于点F.若AB=2,∠AOB=60°,求BF的长.
25.如图,在四边形ABCD中,AD∥BC,AD≠BC,AB∥DE,AF∥DC,E、F两点在BC边上,且BC=3AD.
(1)求证:四边形AEFD是平行四边形.
(2)当AB=DC时,求证:平行四边形AEFD是矩形.
26.如图,在矩形ABCD中,对角线AC、BD交于点O,BE平分∠ABC交AC于点F,交AD于点E,且∠DBF=15°,
求证:(1)AO=AE;
(2)∠FEO的度数.
27.如图,矩形ABCD的对角线AC,BD相交于点O,过点B作AC的平行线交DC的延长线于点E.
(1)求证:BD=BE;
(2)连接OE,若AB=4,BC=6,求OE的长.
参考答案
1.解:A、∵AD∥BC,AD=BC,
∴四边形ABCD是平行四边形,
∵AC=BD,
∴平行四边形ABCD是矩形,故选项A不符合题意;
B、∵AD∥BC,AD=BC,
∴四边形ABCD是平行四边形,∠A+∠B=180°,
∵∠A=∠B,
∴∠A=∠B=90°,
∴平行四边形ABCD是矩形,故选项B不符合题意;
C、∵AD∥BC,
∴∠A+∠B=∠C+∠D=180°,
∵∠A=∠C,
∴∠B=∠D,
∴四边形ABCD是平行四边形,AB=CD,故选项C不符合题意;
D、∵AD∥BC,
∴∠A+∠B=180°,
∵∠A=∠B,
∴∠A=∠B=90°,
∴AB⊥AD,AB⊥BC,AB的长为AD、BC间的距离,
又∵AB=CD,
∴CD⊥AD,
∴∠ADC=90°,
∴四边形ABCD是矩形,
∴选项D不符合题意;
故选:C.
2.解:∵矩形ABCD中,对角线AC,BD相交于点O,
∴OD=OB=OA=OC,
∵∠OAD=40°,
∴∠ODA=∠OAD=40°,
∴∠COD=∠ODA+∠OAD=40°﹣40°=80°,
故选:C.
3.解:不同的划分方法有4种,见图:
所得任一多边形内角和度数可能是360°或540°或180°.
故选:D.
4.解:∵四边形ABCD是矩形,
∴∠B=90°,
∴∠BAC+∠BCA=90°,
∵AE平分∠BAC,AE=CE,
∴∠BAE=∠EAC=∠ECA,
∴∠BAE+∠EAC+∠ECA=90°,
∴∠BAE=∠EAC=∠ECA=30°,
∴AE=CE=2BE=4,AB=2,
∴BC=BE+CE=6,
∴矩形ABCD面积=AB×BC=2×6=12;
故选:C.
5.解:分两种情况讨论:
①当E点在线段DC上时,
∵△AD'E≌△ADE,
∴∠AD'E=∠D=90°,
∵∠AD'B=90°,
∴∠AD'B+∠AD'E=180°,
∴B、D'、E三点共线,
∵,AD'=AD,
∴BE=AB=10,
∵,
∴DE=D'E=10﹣8=2;
②当E点在线段DC的延长线上时,如下图,
∵∠ABD″+∠CBE=∠ABD″+∠BAD″=90°,
∴∠CBE=∠BAD″,
在△ABD″和△BEC中,
∵,
∴△ABD″≌△BEC(ASA),
∴BE=AB=10,
∵,
∴DE=D″E=BD''+BE=8+10=18.
综上所知,DE=2或18.
故选:D.
6.解:连接CM,如图所示:
∵∠ACB=90°,AC=3,BC=4,
∴AB===5,
∵ME⊥AC,MF⊥BC,∠ACB=90°,
∴四边形CEMF是矩形,
∴EF=CM,
∵点P是EF的中点,
∴CP=EF,
当CM⊥AB时,CM最短,
此时EF也最小,则CP最小,
∵△ABC的面积=AB×CM=AC×BC,
∴CM===2.4,
∴CP=EF=CM=1.2,
故选:A.
7.解:由题意,当△ODP是腰长为5的等腰三角形时,有三种情况:
(1)如答图①所示,PD=OD=5,点P在点D的左侧.
过点P作PE⊥x轴于点E,则PE=4.
在Rt△PDE中,由勾股定理得:DE===3,
∴OE=OD﹣DE=5﹣3=2,
∴此时点P坐标为(2,4);
(2)如答图②所示,OP=OD=5.
过点P作PE⊥x轴于点E,则PE=4.
在Rt△POE中,由勾股定理得:OE===3,
∴此时点P坐标为(3,4);
(3)如答图③所示,PD=OD=5,点P在点D的右侧.
过点P作PE⊥x轴于点E,则PE=4.
在Rt△PDE中,由勾股定理得:DE===3,
∴OE=OD+DE=5+3=8,
∴此时点P坐标为(8,4)(舍弃).
综上所述,点P的坐标为:(2,4)或(3,4);
故选:C.
8.解:连接OP,
∵矩形ABCD的两边AB=6,BC=8,
∴S矩形ABCD=AB?BC=48,OA=OC,OB=OD,AC=BD,AC==10,
∴S△AOD=S矩形ABCD=12,OA=OD=5,
∴S△AOD=S△AOP+S△DOP=OA?PE+OD?PF=OA(PE+PF)=×5×(PE+PF)=12,
∴PE+PF==4.8.
故选:C.
9.解:∵四边形ABCD是平行四边形,
∴OA=OC=AC,OB=OD=BD,
A、OD=OC时,AC=BD,
∴平行四边形ABCD是矩形,故选项A不符合题意;
B、四边形ABCD是平行四边形,∠DAB=90°,
∴平行四边形ABCD是矩形,故选项B不符合题意;
C、∵∠ODA=∠OAD,
∴OA=OD,
∴AC=BD,
∴平行四边形ABCD是矩形,故选项C不符合题意;
D、四边形ABCD是平行四边形,AC⊥BD,
∴平行四边形ABCD是菱形,故选项D符合题意;
故选:D.
10.解:过D作DH⊥AF于点H,延长DH与AB相交于点G,
∵四边形ABCD为矩形,
∴AD=BC,
∵DF=BC,
∴DA=DF,
∴AH=FH,
∵AF⊥BE,
∴DG∥BE,
∴AG=BG=,
∵矩形ABCD中,AB=DC=6,AB∥DC,
∴四边形BEDG为平行四边形,
∴DE=BG=3,
∴CE=CD﹣DE=6﹣3=3.
故选:C.
11.解:在矩形ABCD中A(﹣3,2),C(0,4),B(0,2).
∴点D的横坐标为﹣3,纵坐标为4.
∴点D的坐标为(﹣3,4).
故答案为:(﹣3,4).
12.解:过点P作GH∥BC交AB、CD于点G、H,
过P作EF∥AB交AD、BC于点E、F,
设AE=BF=c,AG=DH=a,
GB=HC=b,ED=FC=d,
∴AP2=a2+c2,
CP2=b2+d2,
BP2=b2+c2,
DP2=d2+a2,
∵AP=1,BP=2,CP=3,
∴AP2+CP2=BP2+DP2,
1+9=4+DP2,
DP2=6,
DP=.
故答案为:.
13.解:连接EF、EG、EC,如图所示:
∵四边形ABCD是矩形,
∴BC=AD=6,AD∥BC,∠BAD=∠ABC=90°,
∴AB⊥AD,
∵AF=BF,点E是AB的中点,
∴EF⊥AB,
∴EF∥AD∥BC,
∴EF是梯形ABGD的中位线,∠EFG=∠CGF,
∴EF=(AD+BG),
设BG=x,则CG=6﹣x,EF=(6+x),
∵点C与AB的中点E关于直线DG对称,
∴EG=CG,∠CGF=∠EGF,
∴∠EFG=∠EGF,
∴EG=EF,
∴EF=CG,
∴(6+x)=6﹣x,
解得:x=2,
∴BG=2,EG=CG=4,
∴BE===2.
∴AB=2BE=4;
故答案为:4.
14.解:∵四边形ABCD是矩形,AB=4,AD=6,点E为AB边的中点,点B和点B'关于EF对称,
∴AE=BE=B'E=2,∠A=90°,
∴DE==2,
∴当点B'在线段DE上时,B'D取得最小值,此时B'D=2﹣2,
故答案为:2﹣2.
15.解:∵四边形ABCD是矩形,
∴OA=OC,OB=OD,AC=BD,
∴OA=OB,
∵∠AOB=60°,
∴△OAB是等边三角形,
∴AB=OB=OA=×15=5,
∴AC=BD=2×5=10.
故答案为:10.
16.证明:连接PE,如图
∵BE=ED,PF⊥BE,PG⊥AD,
∴S△BDE=S△BEP+S△DEP==,
又∵四边形ABCD是矩形,
∴BA⊥AD,AB=CD,
∴S△BED=,
∴,
∴PF+PG=AB=CD.
故答案为:AB或CD.
17.解:∵四边形ABCD是矩形,
∴∠A=∠B=90°,AD=BC.
在Rt△ADE中,
∵∠A=90°,∠ADE=30°,DE=4,
∴AE=DE=2,AD=AE=2.
∵DE⊥CE,∠A=90°,
∴∠BEC=∠ADE=90°﹣∠AED=30°.
在Rt△BEC中,
∵∠B=90°,∠BEC=30°,BC=AD=2,
∴BE=BC=6,
∴AB=AE+BE=2+6=8,
∴矩形ABCD的周长=2(AB+AD)=2(8+2)=16+4.
故答案为:16+4.
18.解:∵四边形ABCD是矩形,
∴∠BAD=90°,AD=BC=2cm,
分两种情况:
①点P在AB上时,点Q在D处,如图1所示:
∵△APQ的面积为2cm2,
∴×t×2=2,
解得:t=2;
②点P在BC上时,如图2所示:
∵△APQ的面积为2cm2,
∴×AQ×3=2,
解得:AQ=,
∴DQ=AD﹣AQ=2﹣==2(t﹣3),
解得:t=;
综上所述,当△APQ的面积为2cm2时,t的值为2或;
故答案为:2或.
19.解:根据题意可知:
MN=CD,
∵四边形ABCD是矩形,
∴∠BAD=90°,DC⊥AD,CD=AB=6,
∴MF⊥AD,MN=6,
∵AF平分∠BAD,
∴∠BAF=∠DAF=45°,
∵AB=6,
∴AD=AB=6,
∵DF⊥AF,
∴△ADF是等腰直角三角形,
∴AF=DF,
∴点M是AD的中点,
∴FM=AD=3,FN为△BCH的中位线,
∴FN=MN﹣FM=6﹣3,FN=CH,
∴CH=2FN=12﹣6.
故答案为:12﹣6.
20.解:如图1,当点P在AB上,过点Q作QE⊥AB于E,
∵点B坐标为(24,15),
∴AB=OC=24,AO=BC=15,
∴AP===20,
∵将OP绕点P顺时针旋转90°,
∴OP=PQ,∠OPQ=90°,
∴∠QPE+∠OPA=90°=∠APO+∠AOP,
∴∠QPE=∠AOP,
在△EPQ和△AOP中,
,
∴△EPQ≌△AOP(AAS),
∴EP=AO=15,QE=AP=20,
∴AE=AP﹣EP=5,
∴点Q(5,35);
当点P在BC上时,过点Q作QF⊥BC,交CB的延长线于F,
∴CP===7,
∵将OP绕点P顺时针旋转90°,
∴OP=PQ,∠OPQ=90°,
∴∠QPF+∠OPC=90°,∠OPC+∠POC=90°,
∴∠POC=∠QPF,
在△OPC和△PQF中,
,
∴△OPC≌△PQF(AAS),
∴QF=CP=7,PF=OC=24,
∴CF=31,
∴点Q(17,31),
综上所述:点Q坐标为:(5,35)或(17,31),
故答案为:(5,35)或(17,31).
21.解:∵四边形ABCD是矩形,
∴AD∥BC,∠DCB=90°,
∴∠F=∠ECB=20°,
∴∠GAF=∠F=20°,
∴∠ACG=∠AGC=∠GAF+∠F=2∠F=40°,
∴∠ACB=∠ACG+∠ECB=60°,
∴∠ACD=90°﹣60°=30°,
故答案为:30°.
22.(1)证明:∵四边形ABCD是矩形,
∴AD∥BC,
∴∠BFO=∠DEO,∠FBO=∠EDO,
又∵O是BD中点,
∴OB=OD,
∴△BOF≌△DOE(ASA).
(2)连接BE.
∵EF⊥BD,O为BD中点,
∴EB=ED,
设AE=xcm,由EB=ED=AD﹣AE=(4﹣x)cm,
在Rt△ABE中,AB=3cm,
根据勾股定理得:AB2+AE=BE2,即9+x2=(4﹣x)2,
解得:x=,
∴AE的长是 cm.
23.解:(1)证明:∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD
又∵OA=OB
∴OA=OB=OC=OD
∴AC=BD
∴四边形ABCD是矩形
证法二:
∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD
又∵OA=OB
∴△ABD是以∠BAD为直角的直角三角形,
∴∠BAD=90°
根据矩形的定义知,四边形ABCD是矩形.
(2)∵OA=OB,∠AOB=60°
∴△AOB是等边三角形,
∴OA=OB=AB=2
∴AC=2OA=4
∴在Rt△ABC中,根据勾股定理,有AB2+BC2=AC2
∴BC2=AC2﹣AB2=42﹣22=16﹣4=12
∴BC=
24.(1)证明:∵四边形ABCD是矩形,
∴OA=OB=OC=OD,
∵四边形OCED是平行四边形,
∴四边形OCED为菱形,
∴CE∥OB,CE=OB,
∴四边形OBCE为平行四边形;
(2)解:过F作FM⊥BC于M,过O作ON⊥BC于N,
∵FM⊥BC,ON⊥BC,
∴ON∥FM,
∵AO=OC,
∴ON=AB=1,
∵OF=FC,
∴FM=ON=,
∵∠AOB=60°,OA=OB,
∴∠OAB=60°,∠ACB=30°,
在 Rt△ABC中:
∵AB=2,∠ACB=30°,
∴BC=2,
∵∠ACB=30°,FM=,
∴CM=,
∴BM=BC﹣CM=,
∴BF==.
25.(1)证明:∵AD∥BC,AB∥DE,AF∥DC,
∴四边形ABED和四边形AFCD都是平行四边形.
∵AD=BE,AD=FC,
∵BC=BE+EF+FC=3AD,
∴AD=EF,
∴四边形AEFD是平行四边形;
(2)证明:∵四边形ABED和四边形AFCD都是平行四边形,
∴DE=AB,AF=DC.
∵AB=DC,
∴DE=AF.
又∵四边形AEFD是平行四边形,
∴四边形AEFD是矩形.
26.证明:(1)∵四边形ABCD是矩形,
∴∠BAD=∠ABC=90°,AC=BD,AO=OC,BO=OD,
∴OA=OB,
∵BE平分∠ABC,
∴∠ABE=45°,△ABE为等腰直角三角形,
∴AB=AE.
又∵∠DBF=15°,
∴∠ABO=60°,
∵OA=OB,
∴△AOB是等边三角形,
∴AO=AB,
又∵AB=AE.
∴AO=AE.
(2)由(1)知:△AOB是等边三角形,
∴∠BAO=60°,
∴∠OAE=30°,
又∵AO=AE
∴∠AEO=∠AOE=75°,
∵∠BAE=90°,∠AEB=45°,
∴∠FEO=30°.
27.(1)证明:∵四边形ABCD是矩形,
∴AC=BD,AB∥CD,
又∵BE∥AC,
∴四边形ABEC是平行四边形,
∴AC=BE,
∴BD=BE;
(2)如图,过点O作OF⊥CD于点F,
∵四边形ABCD是矩形,
∴点O是BD的中点,即OB=OD,
∴OF为△BCD的中位线,
∴OF=BC=3,
又∵四边形ABEC是平行四边形,
∴∠BCD=90°,AB=CE=DC=4.
∴CF=DF=CD=2,
∴EF=6.
在直角△OEF中,由勾股定理可得:OE===3.
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
