5.1(2)多边形

(共27张PPT)
猜一猜描写的是一项什么活动？
草长莺飞二月天，拂堤杨柳醉春烟。
儿童散学归来早，忙趁东风放纸鸢。
村居【清】高鼎
三角形
四边形
五边形
六边形
八边形
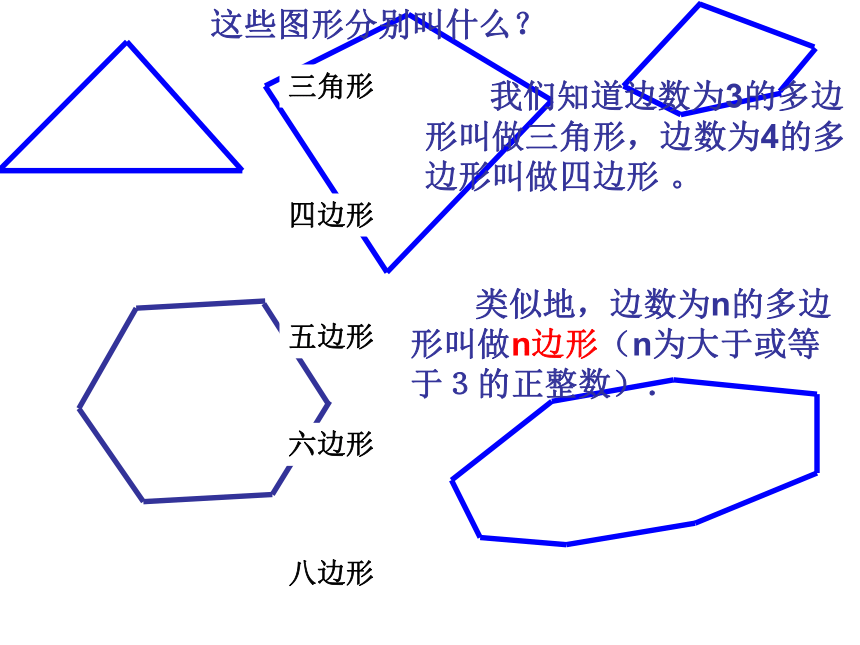
我们知道边数为3的多边形叫做三角形，边数为4的多边形叫做四边形 。
类似地，边数为n的多边形叫做n边形（n为大于或等于３的正整数）．
这些图形分别叫什么？
三角形
四边形
五边形
六边形
八边形
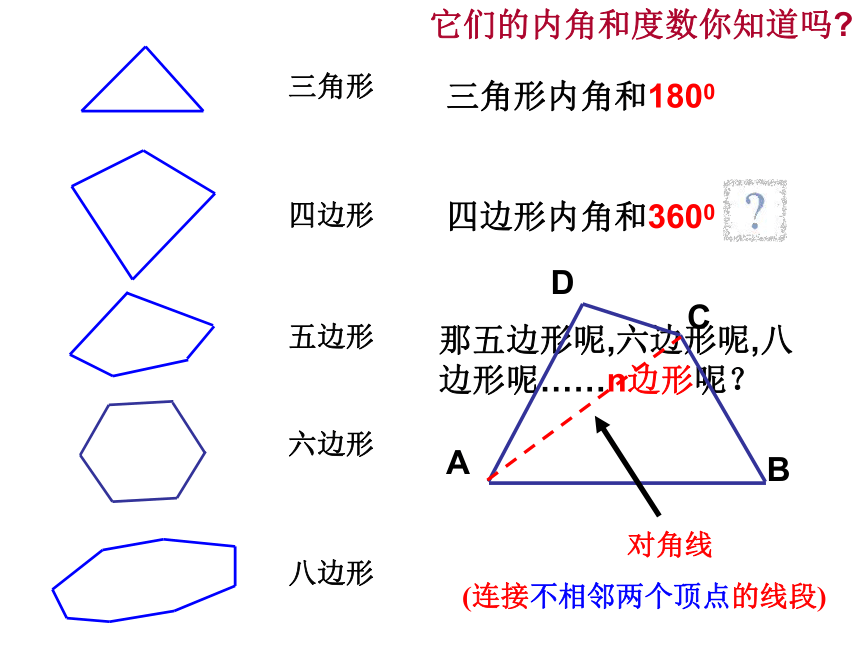
它们的内角和度数你知道吗
三角形内角和1800
四边形内角和3600
那五边形呢,六边形呢,八边形呢……n边形呢？
A
B
C
D
对角线
(连接不相邻两个顶点的线段)
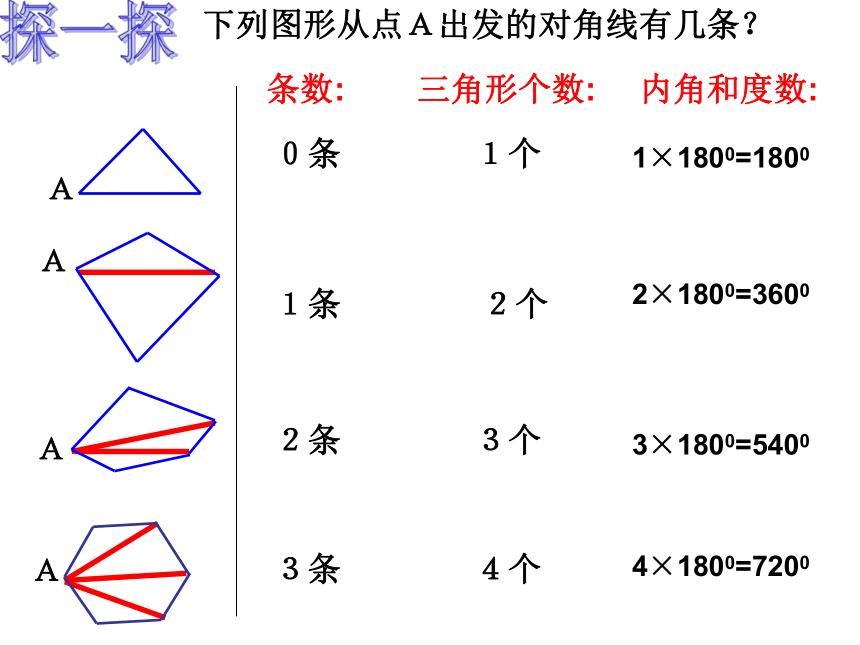
下列图形从点Ａ出发的对角线有几条？
Ａ
Ａ
Ａ
Ａ
０条
１条
２条
３条
１个
２个
３个
４个
1×1800=1800
2×1800=3600
3×1800=5400
4×1800=7200
内角和度数:
条数:
三角形个数:
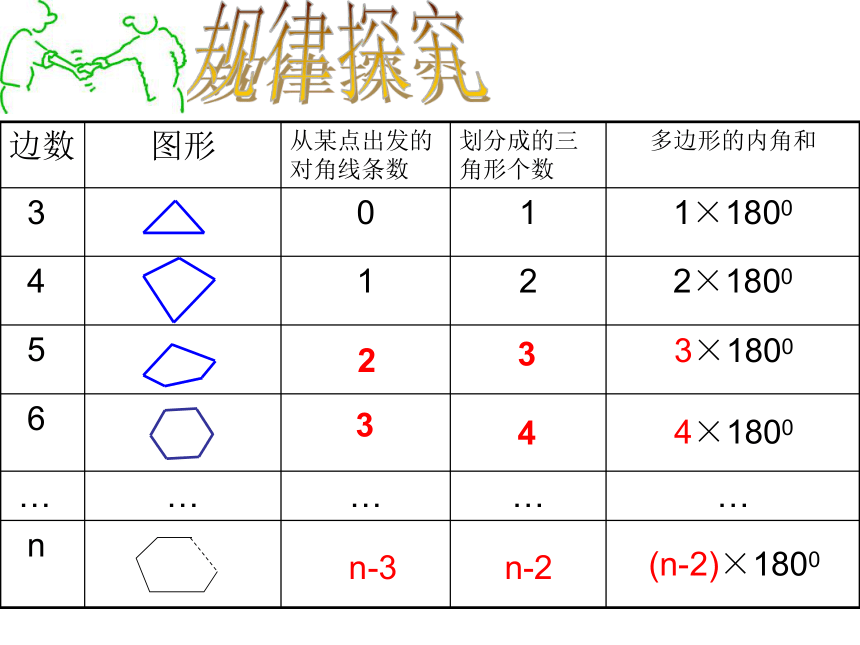
边数 图形 从某点出发的对角线条数 划分成的三角形个数 多边形的内角和
3 0 1 1×1800
4 1 2 2×1800
5
6
… … … … …
n
2
3
n-3
3
4
n-2
3×1800
4×1800
(n-2)×1800
结论：n边形的内角和为：
（n－2）×180°(n≥3).
添对角线是多边形中常用的辅助线
它们的外角和度数呢
3×180°-(3-2)×180°=3600
1
2
3
1
2
3
4
4×180°-(4-2)×180°=360°
边数 图形 多边形的外角和
3 3×180°-(3-2)×180°=360°
4 4×180°-(4-2)×180°=360°
5
6
… … …
n
推论：任何多边形的外角和为360
5×180°-(5-2)×180°=360°
6×180°-(6-2)×180°=360°
n×180°-(n-2)×180°=360°
１、一个十边形的内角和是 　　 度,外角和为 度
２、如果一个多边形的内角和是900度，那么 这是 　 边形。 　　　　 　　　　　　　　
1440
七
内角和=(10-2)×180°=1440 °
外角和=360°
∵(n-2)×180°=900°
∴n=7即为七边形
360
n边形的内角和为：（n－2）×180°(n≥3).
任何多边形的外角和为360
例： 一个六边形如图，已知AB∥DE，BC∥EF，CD∥AF，
A
B
C
D
E
F
(1)求证: ∠A = ∠D
（2）图中还有其他相等的角吗？
（3）求 ∠A+ ∠C+ ∠E的度数
你还有其他解法吗？
连
延
同
旁
（1）已知一个多边形的每一个内角都是108o，求这个多边形的边数为______
5
解法一：设这个多边形的边数为n，由题意得 n×108°= （n-2）×180°
解得:n=5
解法二：设这个多边形的边数为n，已知多边形的每一个内角都是108°，所以它的每个外角是72°，根据多边形外角和等于360°得：n×72°=360°，解得：n=5
（2）在五边形ABCDE中，若∠A=∠D=90o,且 ∠B:∠C:∠E=3:2:4,则∠C的度数为_______
80度
解：由∠B:∠C:∠E=3:2:4
设∠B=3x,∠C=2x,∠E=4x，由题意得：90°+90°+3x+2x+4x=(5-2)×180°
解得：x=40°
所以∠C=2x=2×40°=80°
D
(4)如图，小林从P点向西直走12米后，向左转，转动的角度为α，再走12米，如此重复，小林共走了108米回到点P，则α=（　　）
A、30°
B、40°
C、80°
D、不存在
B
(5)在多边形的外角中，钝角最多有（　　）
A、1个
B、2个
C、3个
D、4个
C
这节课我们学了什么？
:
必做题：
①课本 A组 ②作业本
选做题：
①课本 B组
例： 一个六边形如图，已知AB∥DE，BC∥EF，CD∥AF，
A
B
C
D
E
F
1
2
3
4
(1)求证: ∠A = ∠D
A
B
C
D
E
F
2
R
1
如图所示：可向两个方向分别延长AB，CD
例： 一个六边形如图，已知AB∥DE，BC∥EF， CD∥AF，求证: ∠A = ∠D
A
B
C
D
E
F
例： 一个六边形如图，已知AB∥DE，BC∥EF， CD∥AF，求证: ∠A = ∠D
M
如图所示：延长AB，DC交于点M
A
B
C
D
E
F
例： 一个六边形如图，已知AB∥DE，BC∥EF， CD∥AF，求证: ∠A = ∠D
M
N
如图所示：延长AB，DC交于点M
1
A
B
C
D
1
2
3
4
解：
∵∠1＋∠ABC＝180°，
　∠2＋∠BCD＝180°，
　∠3＋∠ADC＝180°，
　∠4＋∠BAD＝180°，
∴(∠1＋∠2＋∠3＋∠4)
+(∠ABC+∠BCD+∠ADC+∠BAD)
=4×180°
∴∠1＋∠2＋∠3＋∠4
= 4×180°-360°=360°
四边形外角和等于360°