3.1直线和圆的位置关系(1)

(共16张PPT)
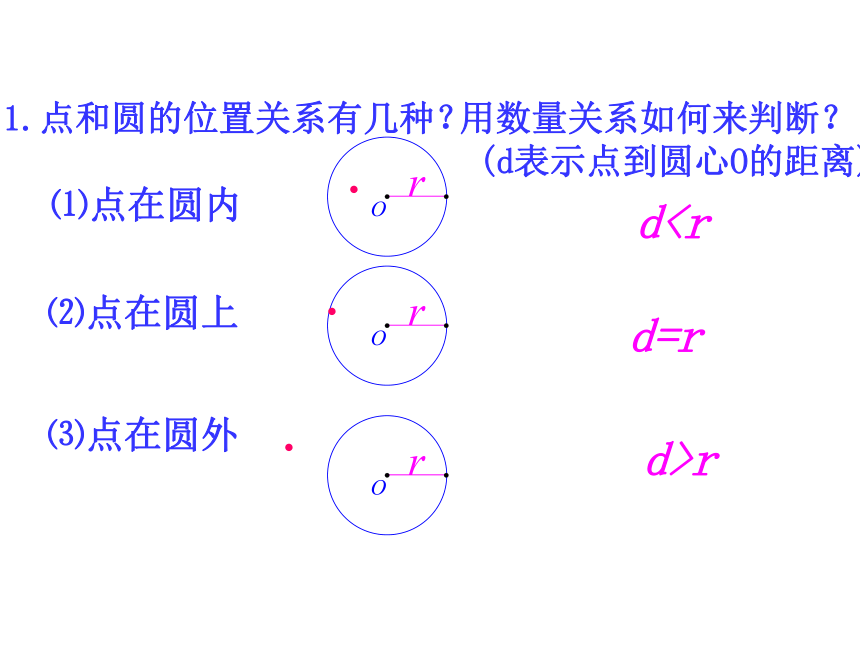
1.点和圆的位置关系有几种？
⑴点在圆内
⑵点在圆上
⑶点在圆外
dd=r
d>r
·
·
·
用数量关系如何来判断？
(d表示点到圆心O的距离)
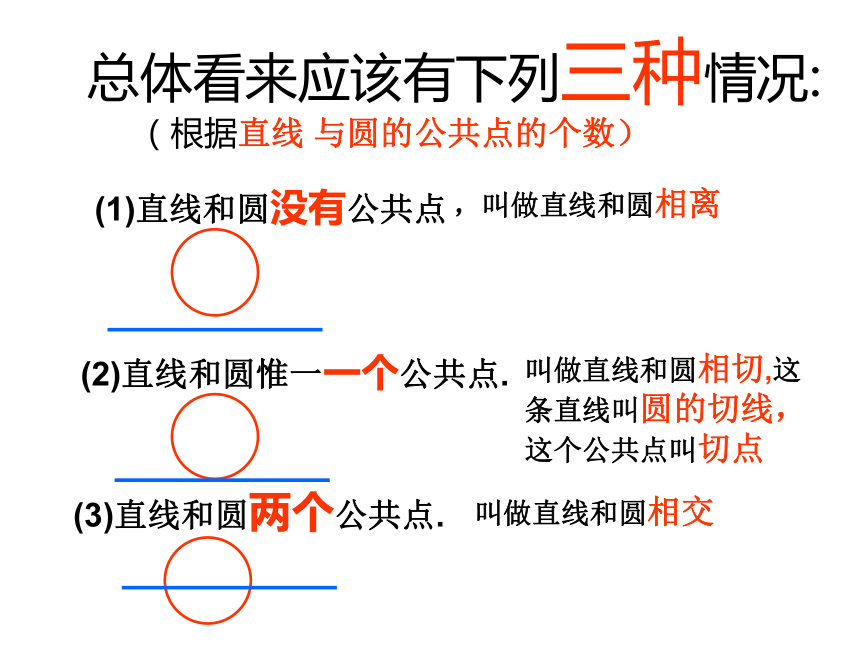
2、如果我们把太阳看成一个圆，地平线看成一条直线,那你能根据直线与圆的公共点的个数想象一下，直线和圆的位置关系有几种？
(1)直线和圆没有公共点
(2)直线和圆惟一一个公共点.
(3)直线和圆两个公共点.
总体看来应该有下列三种情况:
（根据直线 与圆的公共点的个数）
，叫做直线和圆相离
叫做直线和圆相切,这条直线叫圆的切线，这个公共点叫切点
叫做直线和圆相交
用数学的眼光看生活
用数学的眼光看生活
用数学的眼光看生活
如图.O为直线L外一点,OT⊥L,且OT=d.请以O为圆心,分别以 为半径画圆.所画的
圆与直线l有什么位置关系
L
T
O
d
根据圆心到直线的距离d与半径r的关系
d
d
d
.O
.O
.O
r
r
r
相离
相切
相交
1、直线与圆相离 => d>r
2、直线与圆相切 => d=r
3、直线与圆相交 => d<
<
<
l
2
3
.A
.B
.
C
.D
.E
.F
. N
H.
Q.
１设⊙O的半径为r,圆心O到直线L的距离为d,根据下列条件判断直线L与⊙O的位置关系:
d=4,r=3 (2)d=1,r= (3)
(4)
2 在 Rt△ABC 中，∠C = 90°，AC = 3 cm , BC = 4 cm , 以 C 为圆心，r 为半径的圆与 AB 有怎样的关系？为什么？（1）r = 2 cm ; (2) r = 2.4 cm ; (3) r = 3 cm .
解：
过 C 作 CD⊥AB 于 D，在 Rt △ABC 中,
根据三角形面积公式有
CD · AB = AC · BC
即圆心 C 到 AB 的距离 d = 2.4 cm.
(1) 当 r = 2 cm 时，
有 d > r ，因此⊙C 和 AB 相离.
(2) 当 r = 2.4 cm 时，
有 d = r ，因此⊙C 和 AB 相切.
(3) 当 r = 3 cm 时，
有 d < r ，因此⊙C 和 AB 相交.
Ｃ
Ａ
Ｂ
Ｄ
船有无触礁的危险
例：在码头Ａ的北偏东６０°方向有一个海岛，离该岛中心Ｐ点的１２海里范围内是一个暗礁区。货船从码头Ａ由西向东方向航行，行驶了１０海里到达Ｂ点，这时岛中心Ｐ在北偏东４５°方向。
若货船不改变航向，你认为货船会有触礁的危险吗
P
A
B
H
北
600
450
暗礁区
练一练：
　　在南部沿海某气象站A测得一热带风暴从A的南偏东30°的方向迎着气象站袭来，已知该风暴的速度为每小时20千米，风暴周围50千米范围内将受到影响，若该风暴不改变速度和方向，问气象站正南方60千米的沿海城市B是否会受这次风暴的影响？若不受影响，请说明理由；若受影响，请求出受影响的时间。
直线与圆的位置关系
公共点个数
公共点名称
直线名称
数量关系
d r
　无 切线 无
交点 切点 无
2
1
0
直线和圆的三种位置关系
相离
相切
相交
四、课堂小结：
挑战自我
　　在 Rt△ABC 中，∠C = 90°，AC = ６cm , BC = ８cm , 以 C 为圆心，r 为半径画圆
（1）r = ４cm时，圆Ｃ与直线ＡＢ＿＿＿＿＿＿ ;
(2) r = 2.4 cm时，圆Ｃ与直线ＡＢ＿＿＿＿＿＿ ;
(3) r = 3 cm 时，圆Ｃ与直线ＡＢ＿＿＿＿＿＿＿；
（４）若圆Ｃ与斜边ＡＢ只有一个公共点，求r 的取值范围．
布置作业：
1、作业题A
2、B选做