3.1直线与圆的位置关系(3)
图片预览





文档简介
(共15张PPT)
二中备课组
3.1直线与圆的位置关系 (3)
切线的判定方法有:
③、切线的判定定理。
②、直线到圆心的距离等于圆的半径。
①、直线与圆有一个公共点。
切线的判定定理:经过半径外端
并且垂直于这条半径的直线是圆
的切线。
100
200
300
400
500
600
700
600
500
400
300
200
100
P
A
D
B
C
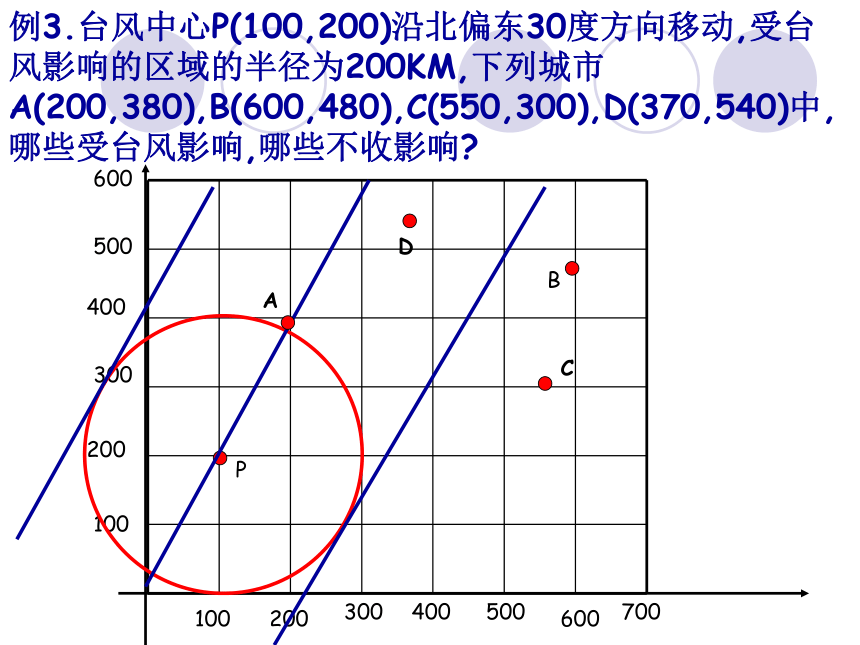
例3.台风中心P(100,200)沿北偏东30度方向移动,受台风影响的区域的半径为200KM,下列城市A(200,380),B(600,480),C(550,300),D(370,540)中,哪些受台风影响,哪些不收影响
⑴、经过半径外端的直线是圆的切线。
⑵、垂直于半径的直线是圆的切线。
⑶、过直径的外端并且垂直于这条直径的
直线是圆的切线。
⑷、和圆只有一个公共点的直线是圆的切
线。
⑸、以等腰三角形的顶点为圆心,底边上
的高为半径的圆与底边相切。
是非题:判断下列命题是否正确。
(×)
(×)
(√)
(√)
(√)
(1)过点P是否都能作这个圆的切线
请任意画一个圆,并在这个圆所在的平面内任意取一点P.
(2)点P在什么位置时,能作且只能作一条切线
(3)点P在什么位置时,能作两条切线 这两条切线有什么特性
(4)能作多于2条的切线吗
1.如图,直线AT与⊙O相切于点A,连结OA,P是AT上一点.∠OAP等于多少度 在⊙O上再任意取一些点,过这些点作⊙O的切线,连结圆心与切点.半径与切线所成的角为多少度 由此你发现了什么
2.任意画一个圆,作这个圆的一条切线.过切点作切线的垂线,你发现了什么 呢发现与你的同伴的发现相同吗
[切线的性质定理]
1.经过切点的半径垂直于圆的切线.
3.经过圆心且垂直于切线的直线必经过切点
2.经过切点且垂直于切线的直线必经过圆心
例1.木工师傅可以用角尺测量并计算出圆的半径,用角尺的较短边紧靠圆O与点A,并使较长边与圆O相切与点C,记角尺的直角顶点为B,若AB=8,BC=16,求圆O的半径.
O
A
B
C
D
1
2
3
O
B
A
C
D
例2、 如图,AB为⊙O的直径, ,AD是和⊙O相切于点A的切线, ⊙O的弦BC平行于OD.
求证:DC是⊙O的切线
4
例3.直线AB与圆O相切与点C,AO交圆O于点D,连接CD,
求证:∠ACD= 1/2∠COD
A
O
C
B
D
E
1、切线和圆只有一个公共点。
2、切线和圆心的距离等于半径。
3、切线垂直于过切点的半径。
4、经过圆心垂直于切线的直线必过切点。
5、经过切点垂直于切线的直线必过圆心。
切线的性质3、4、5可归纳为:已知直线满足a、过圆心,b、过切点,c、垂直于切线中任意两个,便得到第三个结论。
作 业
见: 作 业 本
1、知识:切线的性质:
(1)切线和圆有唯一公共点;(切线的定义)
(2)切线和圆心的距离等于圆的半径;(判定方法(2)的逆命题)
(3)切线垂直于过切点的半径;(切线的性质定理)
(4)经过圆心垂直于切线的直线必过切点;(推论1)
(5)经过切点垂直于切线的直线必过圆心.(推论2)
2、能力和方法:
凡是题目中给出切线的切点,往往“连结”
过切点的半径.从而运用切线的性质定理,
产生垂直的位置关系.
二中备课组
3.1直线与圆的位置关系 (3)
切线的判定方法有:
③、切线的判定定理。
②、直线到圆心的距离等于圆的半径。
①、直线与圆有一个公共点。
切线的判定定理:经过半径外端
并且垂直于这条半径的直线是圆
的切线。
100
200
300
400
500
600
700
600
500
400
300
200
100
P
A
D
B
C
例3.台风中心P(100,200)沿北偏东30度方向移动,受台风影响的区域的半径为200KM,下列城市A(200,380),B(600,480),C(550,300),D(370,540)中,哪些受台风影响,哪些不收影响
⑴、经过半径外端的直线是圆的切线。
⑵、垂直于半径的直线是圆的切线。
⑶、过直径的外端并且垂直于这条直径的
直线是圆的切线。
⑷、和圆只有一个公共点的直线是圆的切
线。
⑸、以等腰三角形的顶点为圆心,底边上
的高为半径的圆与底边相切。
是非题:判断下列命题是否正确。
(×)
(×)
(√)
(√)
(√)
(1)过点P是否都能作这个圆的切线
请任意画一个圆,并在这个圆所在的平面内任意取一点P.
(2)点P在什么位置时,能作且只能作一条切线
(3)点P在什么位置时,能作两条切线 这两条切线有什么特性
(4)能作多于2条的切线吗
1.如图,直线AT与⊙O相切于点A,连结OA,P是AT上一点.∠OAP等于多少度 在⊙O上再任意取一些点,过这些点作⊙O的切线,连结圆心与切点.半径与切线所成的角为多少度 由此你发现了什么
2.任意画一个圆,作这个圆的一条切线.过切点作切线的垂线,你发现了什么 呢发现与你的同伴的发现相同吗
[切线的性质定理]
1.经过切点的半径垂直于圆的切线.
3.经过圆心且垂直于切线的直线必经过切点
2.经过切点且垂直于切线的直线必经过圆心
例1.木工师傅可以用角尺测量并计算出圆的半径,用角尺的较短边紧靠圆O与点A,并使较长边与圆O相切与点C,记角尺的直角顶点为B,若AB=8,BC=16,求圆O的半径.
O
A
B
C
D
1
2
3
O
B
A
C
D
例2、 如图,AB为⊙O的直径, ,AD是和⊙O相切于点A的切线, ⊙O的弦BC平行于OD.
求证:DC是⊙O的切线
4
例3.直线AB与圆O相切与点C,AO交圆O于点D,连接CD,
求证:∠ACD= 1/2∠COD
A
O
C
B
D
E
1、切线和圆只有一个公共点。
2、切线和圆心的距离等于半径。
3、切线垂直于过切点的半径。
4、经过圆心垂直于切线的直线必过切点。
5、经过切点垂直于切线的直线必过圆心。
切线的性质3、4、5可归纳为:已知直线满足a、过圆心,b、过切点,c、垂直于切线中任意两个,便得到第三个结论。
作 业
见: 作 业 本
1、知识:切线的性质:
(1)切线和圆有唯一公共点;(切线的定义)
(2)切线和圆心的距离等于圆的半径;(判定方法(2)的逆命题)
(3)切线垂直于过切点的半径;(切线的性质定理)
(4)经过圆心垂直于切线的直线必过切点;(推论1)
(5)经过切点垂直于切线的直线必过圆心.(推论2)
2、能力和方法:
凡是题目中给出切线的切点,往往“连结”
过切点的半径.从而运用切线的性质定理,
产生垂直的位置关系.
