3.1直线与圆的位置关系(1)

(共14张PPT)
二中备课组
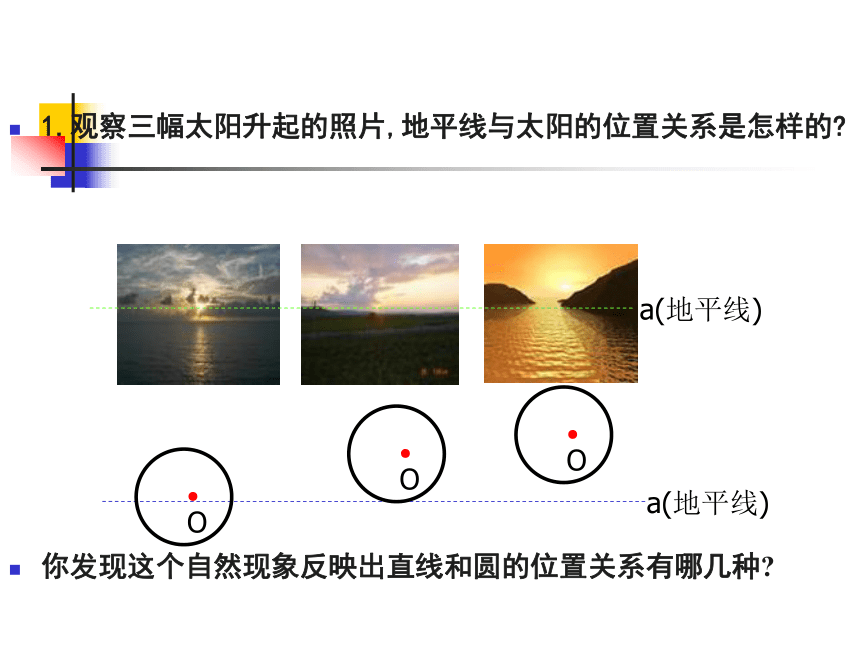
1.观察三幅太阳升起的照片,地平线与太阳的位置关系是怎样的
你发现这个自然现象反映出直线和圆的位置关系有哪几种
a(地平线)
a(地平线)
●O
●O
●O
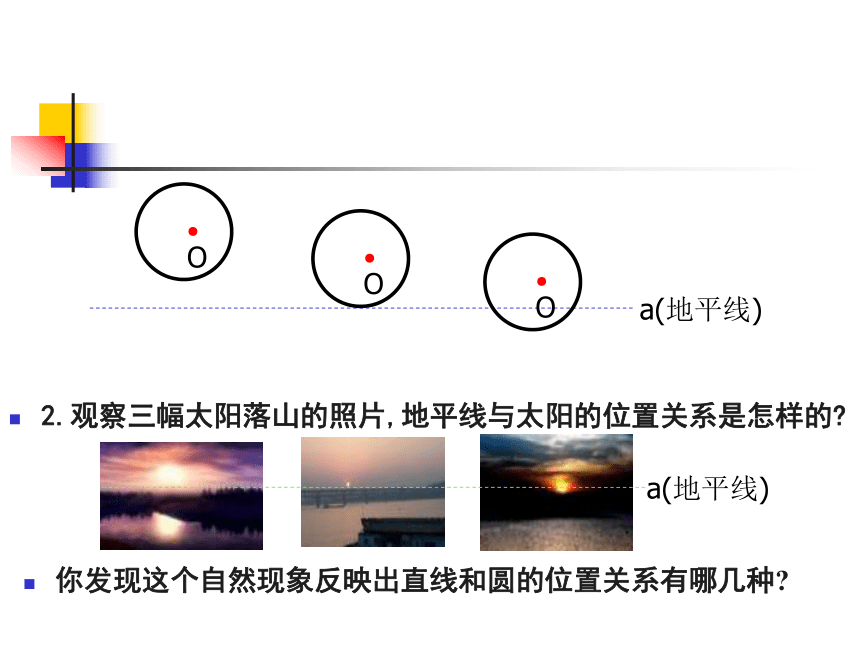
2.观察三幅太阳落山的照片,地平线与太阳的位置关系是怎样的
你发现这个自然现象反映出直线和圆的位置关系有哪几种
a(地平线)
a(地平线)
●O
●O
●O
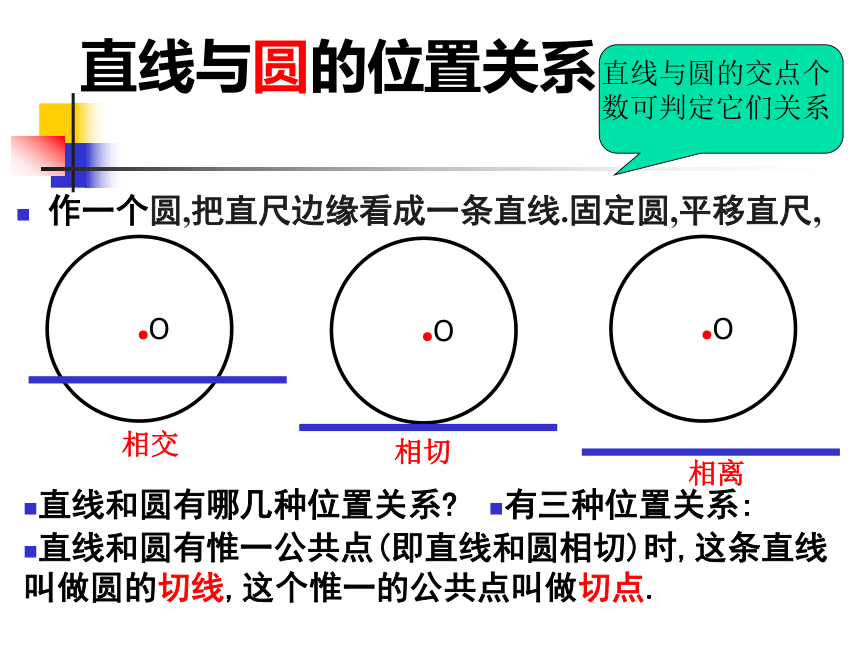
直线与圆的位置关系
作一个圆,把直尺边缘看成一条直线.固定圆,平移直尺,
直线和圆有哪几种位置关系
●O
●O
有三种位置关系:
相交
直线和圆有惟一公共点(即直线和圆相切)时,这条直线叫做圆的切线,这个惟一的公共点叫做切点.
●O
相切
相离
直线与圆的交点个数可判定它们关系
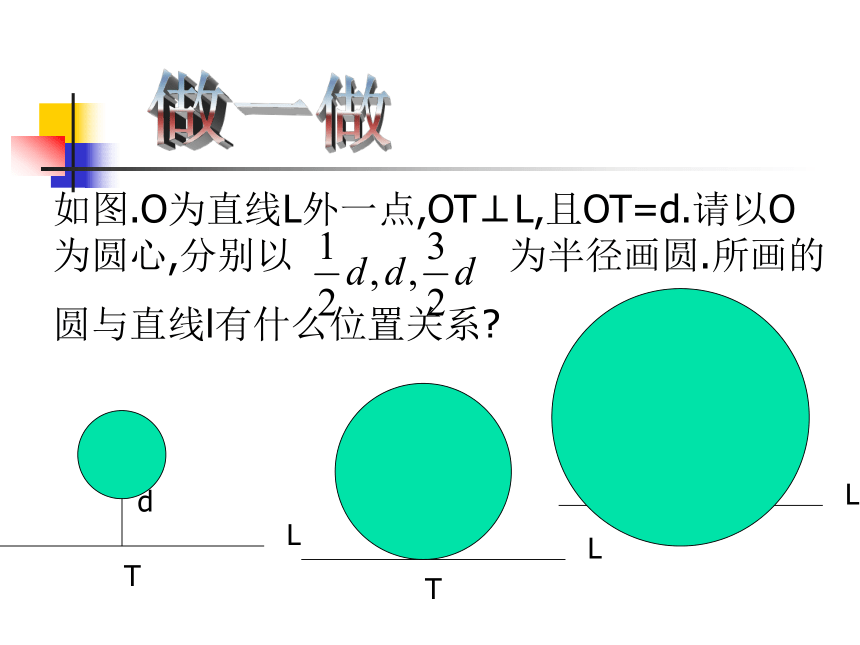
如图.O为直线L外一点,OT⊥L,且OT=d.请以O为圆心,分别以 为半径画圆.所画的
圆与直线l有什么位置关系
L
T
O
d
L
T
O
d
L
T
O
d
如图,圆心O到直线l的距离d与⊙O的半径r的大小有什么关系
你能根据d与r的大小关系确定直线与圆的位置关系吗
●O
●O
相交
●O
相切
相离
直线与圆的位置关系量化
r
r
r
┐d
d
┐
d
┐
直线和圆相交
d r;
d r;
直线和圆相切
直线和圆相离
d r;
直线与圆的位置关系量化
●O
●O
相交
●O
相切
相离
r
r
r
┐d
d
┐
d
┐
<
=
>
1.设⊙O的半径为r,圆心O到直线L的距离为d,根据下列条件判断直线L与⊙O的位置关系:
d=4,r=3 (2)d=1,r= (3)
(4)
2.在直角三角形ABC 中, ∠ACB=90°,CA=3,CB=4.设⊙C 的半径为r. 请根据r的下列值,判断AB与⊙C 的位置关系,并说明理由.
(1) r=2 (2) r=2.4 (3) r=3
1.已知Rt△ABC的斜边AB=8cm,直角边AC=4cm.
以点C为圆心作圆,当半径为多长时,AB与⊙C相切
A
C
B
┐
D
┛
例1；
1、船有无触礁的危险
如图,海中有一个小岛P,该岛四周12海里内暗礁.今有货轮四由西向东航行,开始在A点观测P在北偏东600处, 行驶10海里后到达B点观测P在北偏东450处,货轮继续向东航行.
要解决这个问题,我们可以将其数学化,如图:
请与同伴交流你是怎么想的 怎么去做
你认为货轮继续向东航行途中会有触礁的危险吗
P
A
B
H
北
例2；
600
450
你说我说大家说
下课了!
学到了什么
还有什么疑惑与不解
直线和圆的位置关系
直线和圆的位置 相交 相切 相离
图形
公共点个数
圆心到直线距离 d与半径r的关系
公共点名称
直线名称
2
1
0
dd=r
d>r
交点
切点
无
割线
切线
无
O

d
r
O
l

d
r
O

d
r