1.3解直角三角形的应用(1)
图片预览



文档简介
(共15张PPT)
1.3 解直角三角形
我们已经掌握了直角三角形边角之间的各种关系,这些都是解决与直角三角形有关的实际问题的有效工具.
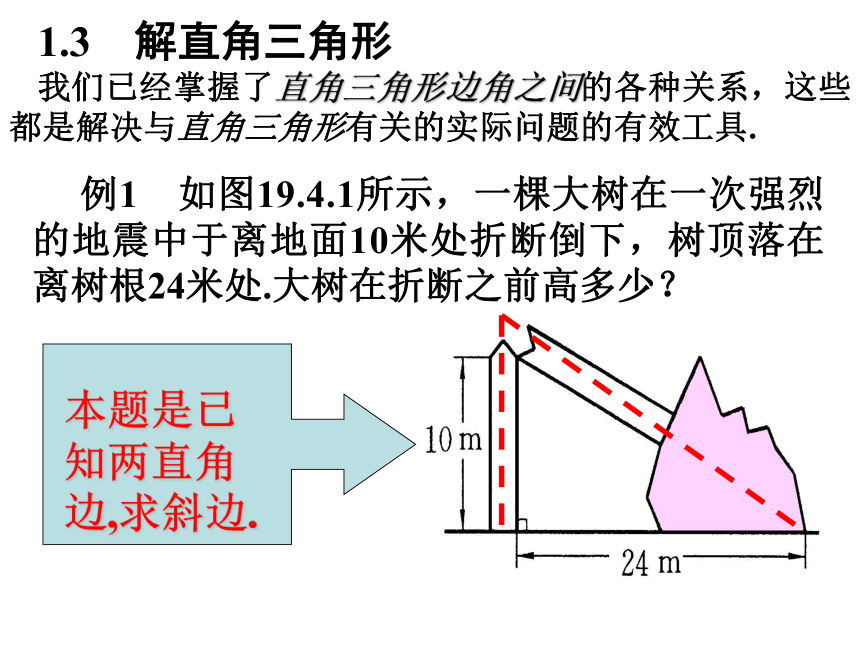
例1 如图19.4.1所示,一棵大树在一次强烈的地震中于离地面10米处折断倒下,树顶落在离树根24米处.大树在折断之前高多少?
本题是已知两直角边,求斜边.
§19.4 解直角三角形
我们已经掌握了直角三角形边角之间的各种关系,这些都是解决与直角三角形有关的实际问题的有效工具.
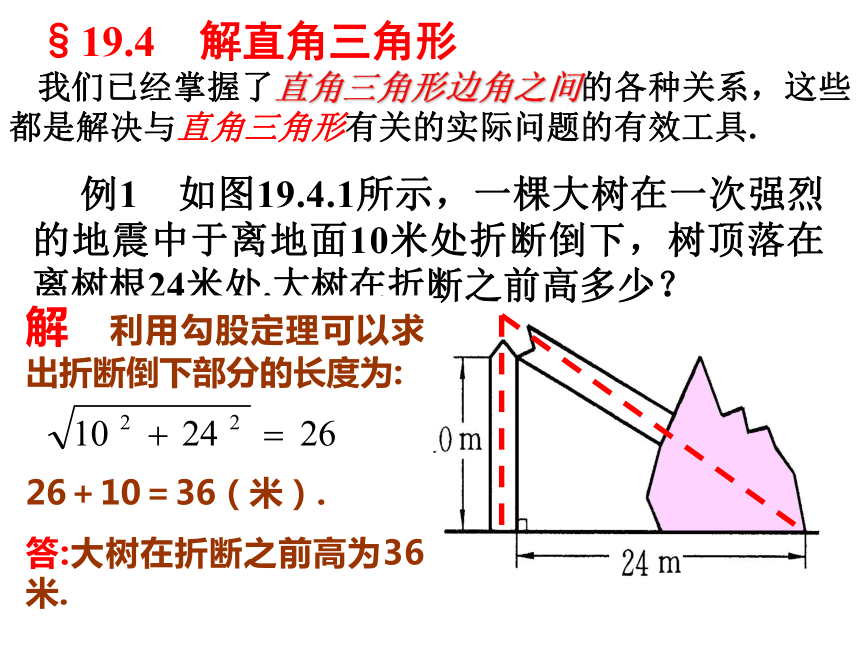
例1 如图19.4.1所示,一棵大树在一次强烈的地震中于离地面10米处折断倒下,树顶落在离树根24米处.大树在折断之前高多少?
解 利用勾股定理可以求出折断倒下部分的长度为:
26+10=36(米).
答:大树在折断之前高为36米.
在例1中,我们还可以利用直角三角形的边角之间的关系求出另外两个锐角.像这样,
********************************
在直角三角形中,由已知元素求出未知元素的过程,叫做解直角三角形.
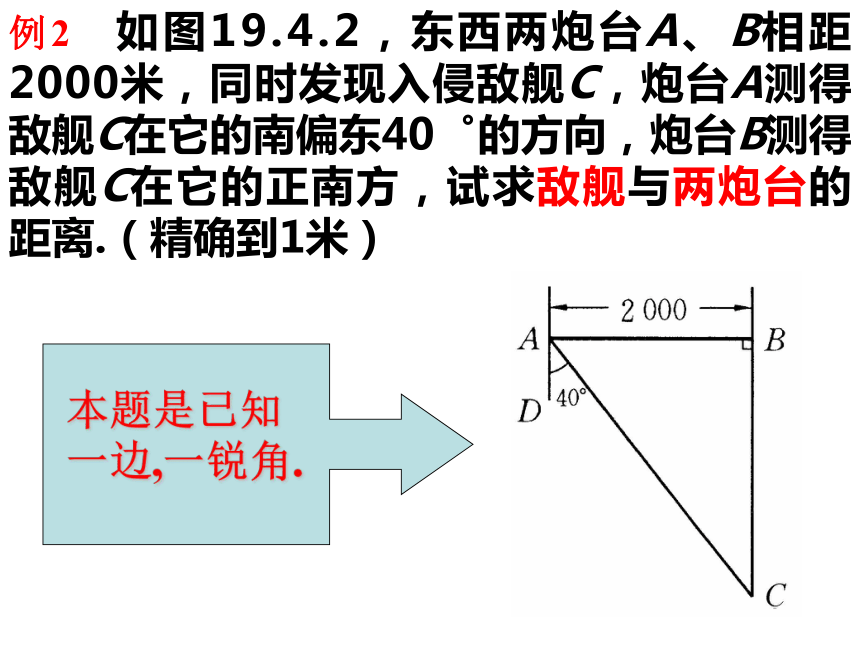
例2 如图19.4.2,东西两炮台A、B相距2000米,同时发现入侵敌舰C,炮台A测得敌舰C在它的南偏东40゜的方向,炮台B测得敌舰C在它的正南方,试求敌舰与两炮台的距离.(精确到1米)
本题是已知一边,一锐角.
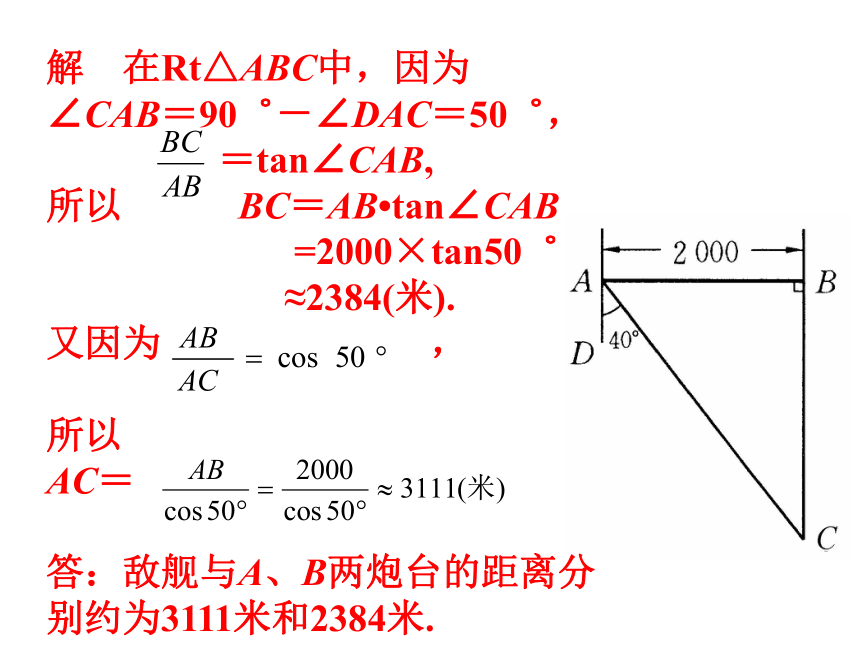
解 在Rt△ABC中,因为
∠CAB=90゜-∠DAC=50゜,
=tan∠CAB,
所以 BC=AB tan∠CAB
=2000×tan50゜
≈2384(米).
又因为 ,
所以
AC=
答:敌舰与A、B两炮台的距离分别约为3111米和2384米.
在解直角三角形的过程中,常会遇到近似计算,本书除特别说明外, 边长保留四个有效数字,角度精确到1′.
解直角三角形,只有下面两种情况:
(1)已知两条边;
(2)已知一条边和一个锐角
精确度:
边长保留四个有效数字,角度精确到1′.
两种情况:
解直角三角形,只有下面两种情况:
(1)已知两条边;
(2)已知一条边和一个锐角
1. 解直角三角形.
在直角三角形中,由已知元素求出未知元素的过程,叫做解直角三角形.
如图19.4.3, 在进行测量时,从下向上看,视线与水平线的夹角叫做仰角;从上往下看,视线与水平线的夹角叫做俯角.
19.4.3
例3
如图19.4.4,为了测量电线杆的高度AB,在离电线杆22.7米的C处,用高1.20米的测角仪CD测得电线杆顶端B的仰角a=22°,求电线杆AB的高.(精确到0.1米)
你会解吗?
例3
如图,为了测量电线杆的高度AB,在离电线杆22.7米的C处,用高1.20米的测角仪CD测得电线杆顶端B的仰角a=22°,求电线杆AB的高.(精确到0.1米)
在Rt△BDE中,
∵ BE=DE×tan a
=AC×tan a
∴AB=BE+AE = AC×tan a +CD =9.17+1.20≈10.4(米)
答: 电线杆的高度约为10.4米.
解:
如图,某飞机于空中A处探测到目标C,此时飞行高度AC=1200米,从飞机上看地面控制点B的俯角 a=16゜31′,求飞机A到控制点B的距离.(精确到1米)
如图所示,站在离旗杆BE底部10米处的D点,目测旗杆的顶部,视线AB与水平线的夹角∠BAC为34°,并已知目高AD为1米.算出旗杆的实际高度.(精确到1米)
例1、学校操场上有一根旗杆,上面有一根开旗用的绳子(绳子足够长),王同学拿了一把卷尺,并且向数学老师借了一把含300的三角板去度量旗杆的高度。
(1)若王同学将旗杆上绳子拉成仰角为600,如图用卷尺量得BC=4米,则旗杆AB的高多少?
(2)若王同学分别在点C、点D处将旗杆上绳子分别拉成仰角为600、300,如图量出CD=8米,你能求出旗杆AB的长吗?
(3)此时他的数学老师来了一看,建议王同学只准用卷尺去量,你能给王同学设计方案完成任务吗?
A
B
4m
600
A
B
D
8m
300
600
设计方案测量下面两幢楼的高度。写出需要的数据并画出示意图、给出计算方案。
1.3 解直角三角形
我们已经掌握了直角三角形边角之间的各种关系,这些都是解决与直角三角形有关的实际问题的有效工具.
例1 如图19.4.1所示,一棵大树在一次强烈的地震中于离地面10米处折断倒下,树顶落在离树根24米处.大树在折断之前高多少?
本题是已知两直角边,求斜边.
§19.4 解直角三角形
我们已经掌握了直角三角形边角之间的各种关系,这些都是解决与直角三角形有关的实际问题的有效工具.
例1 如图19.4.1所示,一棵大树在一次强烈的地震中于离地面10米处折断倒下,树顶落在离树根24米处.大树在折断之前高多少?
解 利用勾股定理可以求出折断倒下部分的长度为:
26+10=36(米).
答:大树在折断之前高为36米.
在例1中,我们还可以利用直角三角形的边角之间的关系求出另外两个锐角.像这样,
********************************
在直角三角形中,由已知元素求出未知元素的过程,叫做解直角三角形.
例2 如图19.4.2,东西两炮台A、B相距2000米,同时发现入侵敌舰C,炮台A测得敌舰C在它的南偏东40゜的方向,炮台B测得敌舰C在它的正南方,试求敌舰与两炮台的距离.(精确到1米)
本题是已知一边,一锐角.
解 在Rt△ABC中,因为
∠CAB=90゜-∠DAC=50゜,
=tan∠CAB,
所以 BC=AB tan∠CAB
=2000×tan50゜
≈2384(米).
又因为 ,
所以
AC=
答:敌舰与A、B两炮台的距离分别约为3111米和2384米.
在解直角三角形的过程中,常会遇到近似计算,本书除特别说明外, 边长保留四个有效数字,角度精确到1′.
解直角三角形,只有下面两种情况:
(1)已知两条边;
(2)已知一条边和一个锐角
精确度:
边长保留四个有效数字,角度精确到1′.
两种情况:
解直角三角形,只有下面两种情况:
(1)已知两条边;
(2)已知一条边和一个锐角
1. 解直角三角形.
在直角三角形中,由已知元素求出未知元素的过程,叫做解直角三角形.
如图19.4.3, 在进行测量时,从下向上看,视线与水平线的夹角叫做仰角;从上往下看,视线与水平线的夹角叫做俯角.
19.4.3
例3
如图19.4.4,为了测量电线杆的高度AB,在离电线杆22.7米的C处,用高1.20米的测角仪CD测得电线杆顶端B的仰角a=22°,求电线杆AB的高.(精确到0.1米)
你会解吗?
例3
如图,为了测量电线杆的高度AB,在离电线杆22.7米的C处,用高1.20米的测角仪CD测得电线杆顶端B的仰角a=22°,求电线杆AB的高.(精确到0.1米)
在Rt△BDE中,
∵ BE=DE×tan a
=AC×tan a
∴AB=BE+AE = AC×tan a +CD =9.17+1.20≈10.4(米)
答: 电线杆的高度约为10.4米.
解:
如图,某飞机于空中A处探测到目标C,此时飞行高度AC=1200米,从飞机上看地面控制点B的俯角 a=16゜31′,求飞机A到控制点B的距离.(精确到1米)
如图所示,站在离旗杆BE底部10米处的D点,目测旗杆的顶部,视线AB与水平线的夹角∠BAC为34°,并已知目高AD为1米.算出旗杆的实际高度.(精确到1米)
例1、学校操场上有一根旗杆,上面有一根开旗用的绳子(绳子足够长),王同学拿了一把卷尺,并且向数学老师借了一把含300的三角板去度量旗杆的高度。
(1)若王同学将旗杆上绳子拉成仰角为600,如图用卷尺量得BC=4米,则旗杆AB的高多少?
(2)若王同学分别在点C、点D处将旗杆上绳子分别拉成仰角为600、300,如图量出CD=8米,你能求出旗杆AB的长吗?
(3)此时他的数学老师来了一看,建议王同学只准用卷尺去量,你能给王同学设计方案完成任务吗?
A
B
4m
600
A
B
D
8m
300
600
设计方案测量下面两幢楼的高度。写出需要的数据并画出示意图、给出计算方案。
