6。1矩形(1-3)

(共34张PPT)
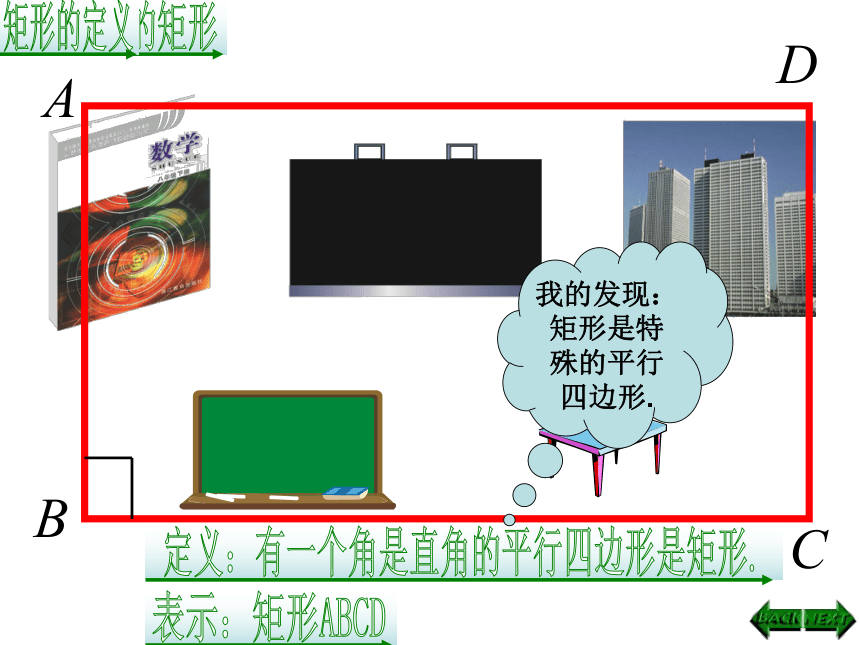
我的发现：矩形是特殊的平行四边形.
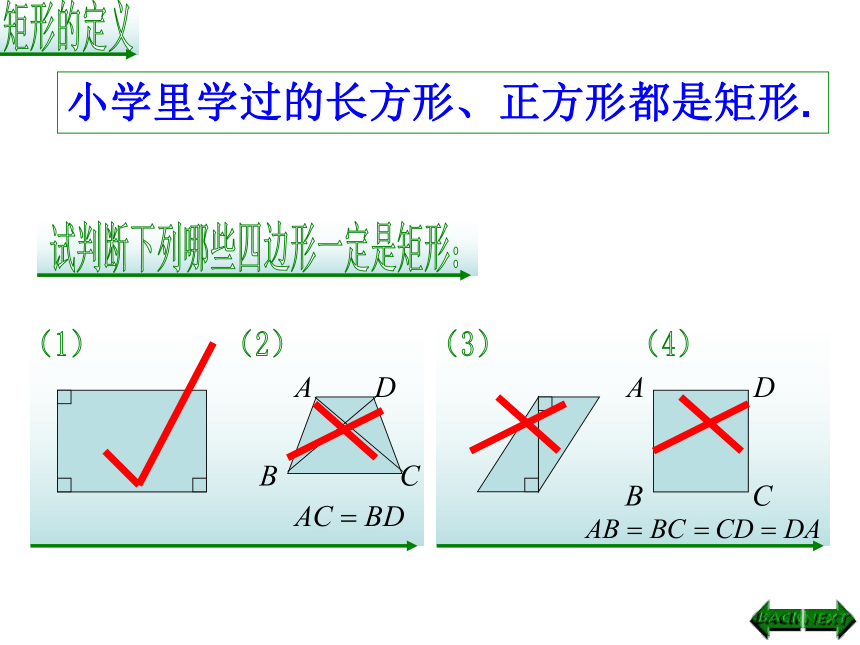
小学里学过的长方形、正方形都是矩形.
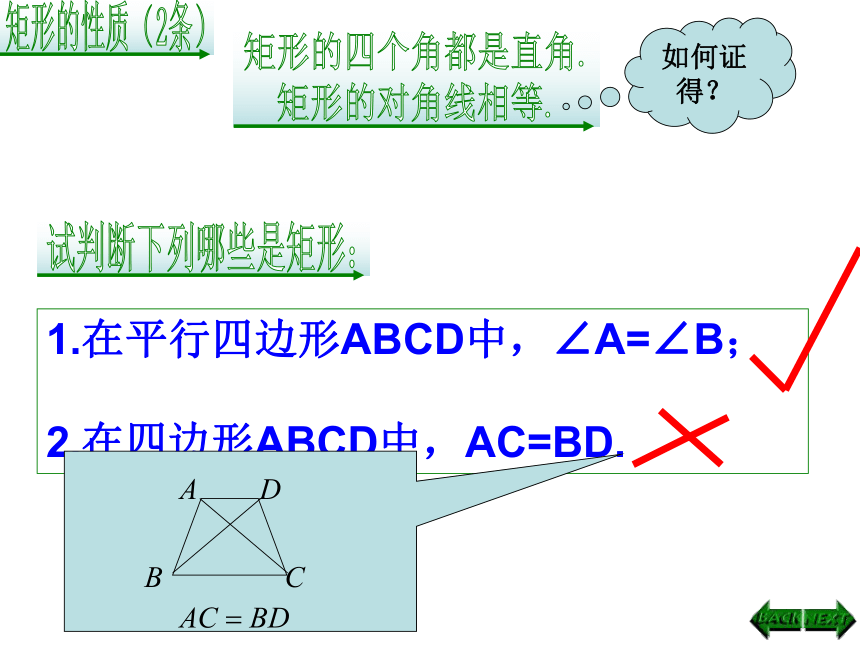
1.在平行四边形ABCD中，∠A=∠B；
2.在四边形ABCD中，AC=BD.
如何证得？
1.平行四边形具有的性质矩形也一定具有；
2.矩形具有的性质平行四边形也一定具有.
请举出反例.（从边、角、线三方面考虑.）
请注意区分平行四边形与矩形的关系与性质.
A
B
C
D
O
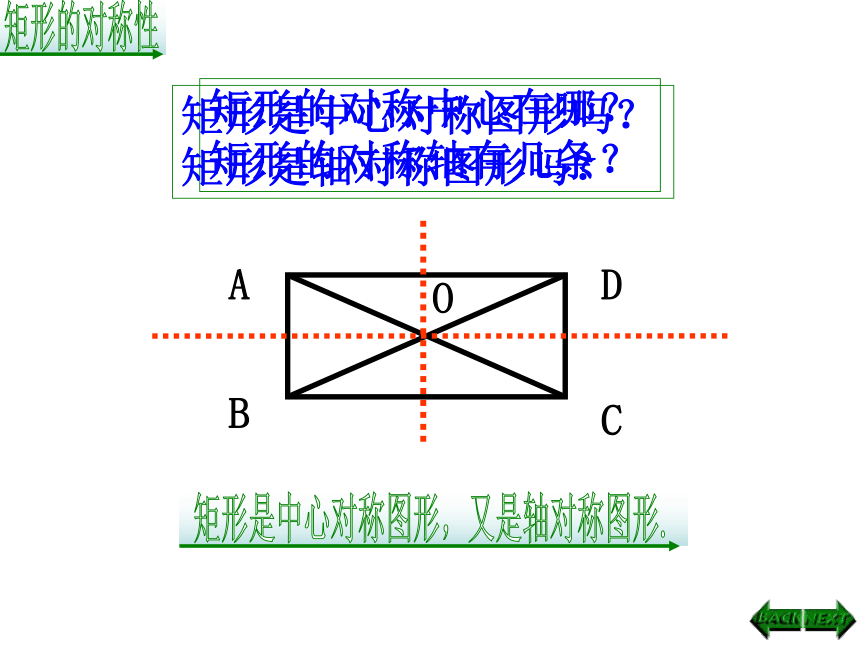
矩形的对称中心在哪？
矩形的对称轴有几条？
矩形是中心对称图形吗？
矩形是轴对称图形吗？
矩形的一对角线与一边的夹角是50°，
则这两条对角线所夹的锐角为_______.
80o
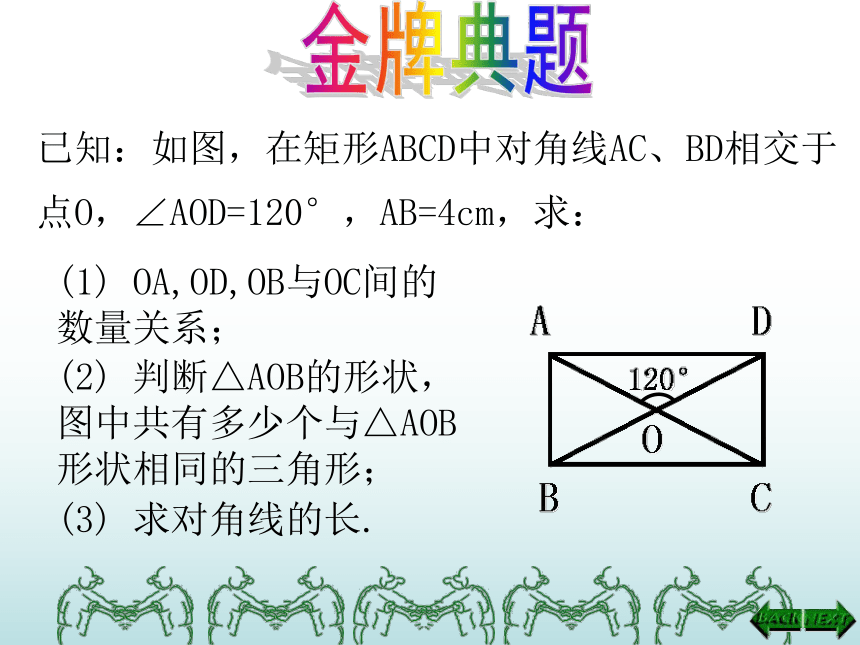
已知：如图，在矩形ABCD中对角线AC、BD相交于点O，∠AOD=120°，AB=4cm，求：
(2) 判断△AOB的形状，图中共有多少个与△AOB 形状相同的三角形；
(3) 求对角线的长.
(1) OA,OD,OB与OC间的数量关系；
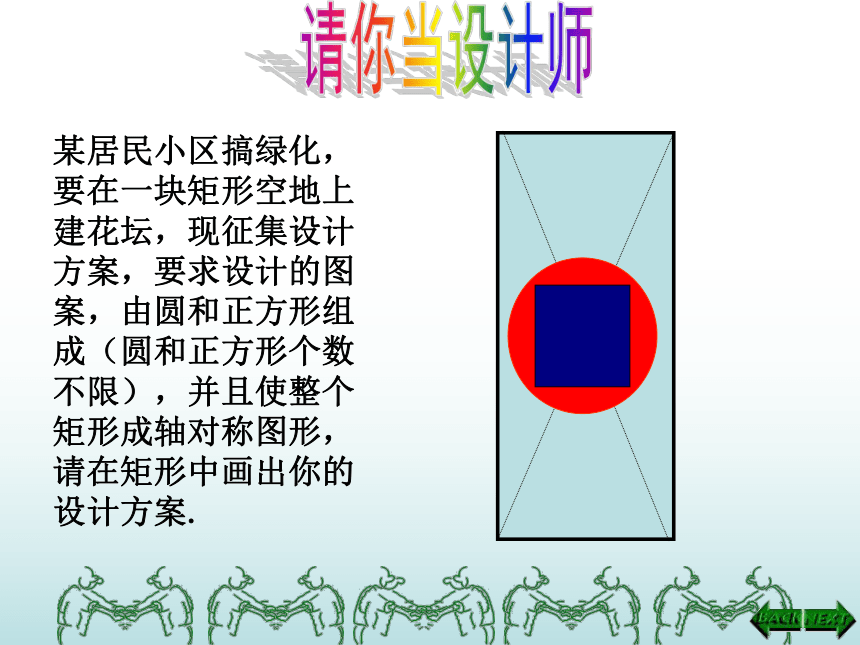
某居民小区搞绿化，要在一块矩形空地上建花坛，现征集设计方案，要求设计的图案，由圆和正方形组成（圆和正方形个数不限），并且使整个矩形成轴对称图形，请在矩形中画出你的设计方案.
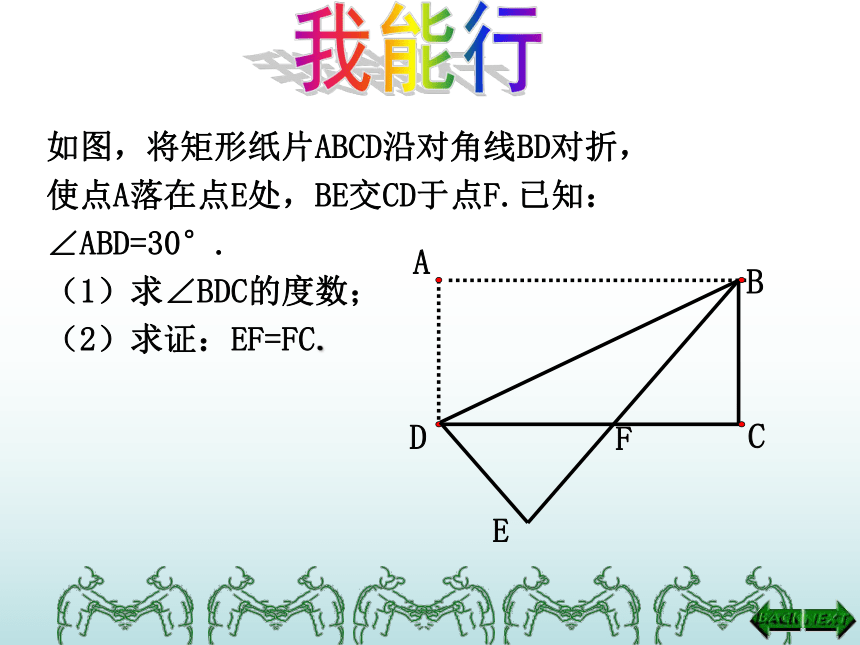
如图，将矩形纸片ABCD沿对角线BD对折，
使点A落在点E处，BE交CD于点F.已知：
∠ABD=30°.
（1）求∠BDC的度数；
（2）求证：EF=FC.
B
A
D
C
F
E
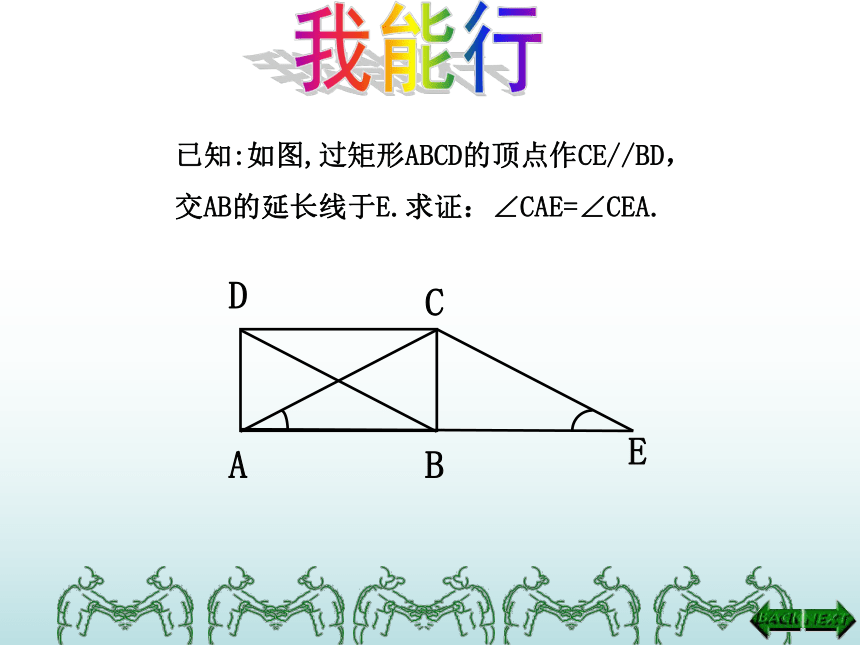
已知:如图,过矩形ABCD的顶点作CE//BD，
交AB的延长线于E.求证：∠CAE=∠CEA.
A
B
C
D
E
如图，在矩形ABCD中,AD=4cm，AB=3cm，BE垂直于
AC于点E，求BE的长.
A D
E
B C
①对边平行且相等;
②对角相等,邻角互补;
③对角线互相平分;
④它是中心对称图形.
一般情况下，我们判断某一事物，会运用该事物的定义进行判定.然而，我们也可采取其它的办法.
我们学过判定平行四边形的多种方法，其中除定义以外，还有其它方法可以判定.
请回顾平行四边行的定义.
请回顾判定平行四边行的办法.
定义.
如图，在四边形ABCD中，AB//CD，
∠D=90°，∠A=∠C，求证：
四边形ABCD是矩形.
证明：
A
B
C
D
在四边形ABCD中，
∵AB//CD，
∴∠D+∠A=180°（ ）.
两直线平行，同旁内角互补
又∵∠D=90°，∠A=∠C，
∴∠A=180°-90°=90°=∠C.
∴四边形ABCD是矩形（ ）.
有三个角是直角
的四边形是矩形
如图，四边形ABCD是矩形，点E、
F、G、H分别是AB、BC、CD、AD的
中点，连结EF、FG、GH、HE；
点W、X、Y、Z分别是HE、EF、HG、
GF的中点，连结XY、YZ、WY、XW.
求证：四边形WXYZ是矩形.
简要分析：
A E
H
B
F
C
D G
W X
Y Z
连结EG、HF，使其交
于O点，可证四边形EBCG是矩形
（EB平行且等于GC,得其为平行
四边形，再由一个角为Rt∠得
矩形），同理证得四边形BAHF
是矩形，整理可得∠EOF是直角.
利用中位线的性质，得到所需
平行线后，将∠EOF转递至四边
形WXYZ各个顶角,从而得知四边
形WXYZ是矩形.
0
你还有其它办法吗？
继续探索特殊四边形的奥秘，或许将会更简单.
已知：如图，AC与BD相交于点O，AB CD且∠1=∠2 . 求证：四边形ABCD是矩形.
如图，在 ABCD中，以AC为斜边作Rt△AMC，且
∠BMD为直角.求证： ABCD是矩形.
M
D
A
B C
0
直角三角形斜边上的中点等于斜边的一半.
判断下列定义或定理的表述是否完全正确（错误请给予改正）：
矩形有哪些性质？
①对边平行且相等;
②对角相等,邻角互补;
③对角线互相平分;
④它是中心对称图形.
矩形有哪些判定方法？
在Rt△ABC中，∠B=90°，O是AC 的中点，连结DB，AB= 3 ，BC=1，求AC的值.
A
B
C
你是用什么方法解决这个问题的？
O
A
B
C
O
我们已经知道：直角三角形斜边上的中线等于斜边的一半.
现在，我们将该性质运用于矩形的学习中.
D
（1）在Rt△ABC中，∠C=Rt∠，AC=BC=1，则AB边上的中线长为
_______.
（2）如图，一斜坡AB的中点为D，BC=1，CD=2，则：
斜坡的坡比为______________.
（3）如图，在矩形ABCD中，E是BC的中点，∠BAE=30°，AE=2，则BD=______________.
如图，在 ABCD中，以AC为斜边作Rt△AMC，且
∠BMD为直角.求证： ABCD是矩形.
M
D
A
B C
0
连结BD交AC于点O，连结MO……
（通过以上学习，请同学们独立完
成该题证明过程）
如图，在Rt△ABC中，∠ACB=90°，P为AB边的中点，过点P作PE⊥AC于点F，PF⊥PC于点F.求证：EF= AB.
A
E P
C F B
1
2
已知：如图，在四边形ABCD中，∠ABC=∠ADC=Rt∠，M是AC的中点，N是BD的中点. 试判断MN与BD的位置关系，并加以证明.
已知：如图，△ABC中，BD，CD是高，G、F分别是BC，DE的中点.试判断FG与DE的位置关系，并加以证明.
如图，在Rt△AED和Rt△ABD中，∠AED=∠DBA=90°，
请添加条件和求证内容，并试着证明.
A
B
C
D
E
如添加：
条件：AC=DC；
求证：CE=CB.
我来添加：
条件： ；
求证： ；
证明过程：
.
填一填：