比例线段的两个基本图形

(共63张PPT)
比例线段的
两个基本图形
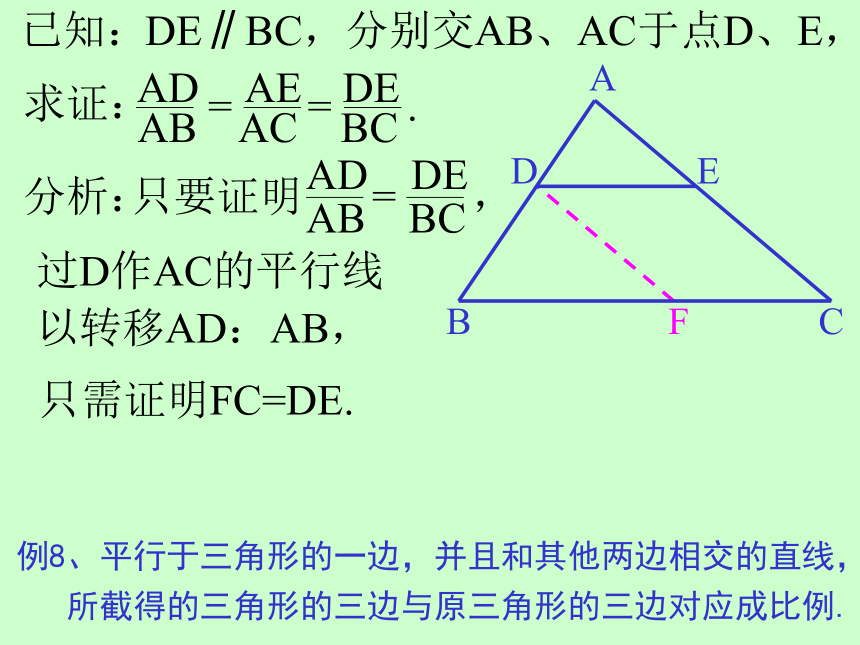
例8、平行于三角形的一边，并且和其他两
边相交的直线，所截得的三角形的三
边与原三角形的三边对应成比例.
例8、平行于三角形的一边，并且和其他两边相交的直线，
所截得的三角形的三边与原三角形的三边对应成比例.
已知：
D
A
B
C
E
F
DE∥BC，分别交AB、AC于点D、E，
求证：
AB AC BC
= = .
AD
AE
DE
分析：
只要证明
AD DE
AB BC
= ，
过D作AC的平行线
只需证明FC=DE.
以转移AD：AB，
已知：
D
A
B
C
E
F
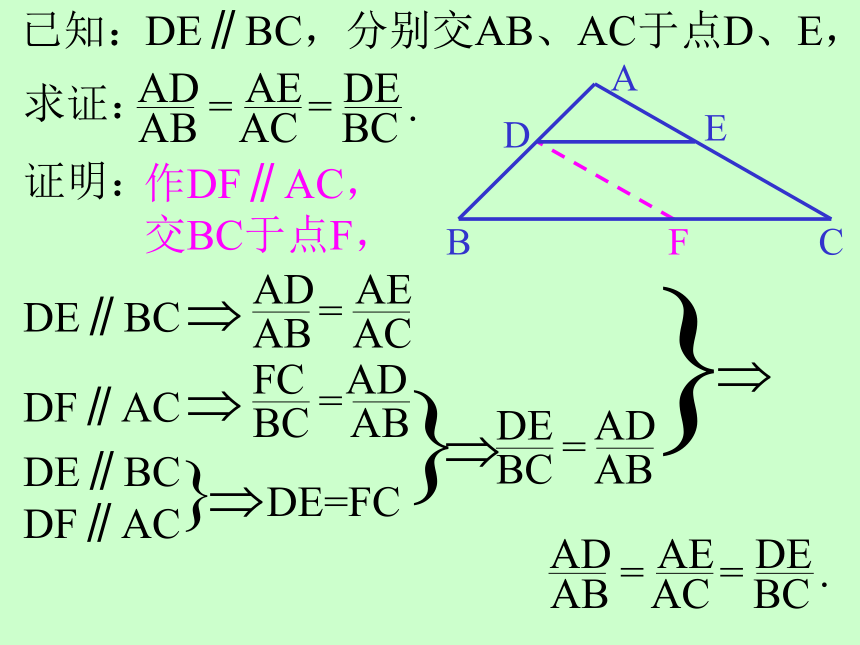
DE∥BC，分别交AB、AC于点D、E，
求证：
AD AE
AB AC
=
证明：
作DF∥AC，
交BC于点F，
DE∥BC
FC AD
BC AB
=
DF∥AC
DE AD
BC AB
=
DE∥BC
DF∥AC
}
DE=FC
}
}
AB AC BC
= = .
AD
AE
DE
AB AC BC
= = .
AD
AE
DE
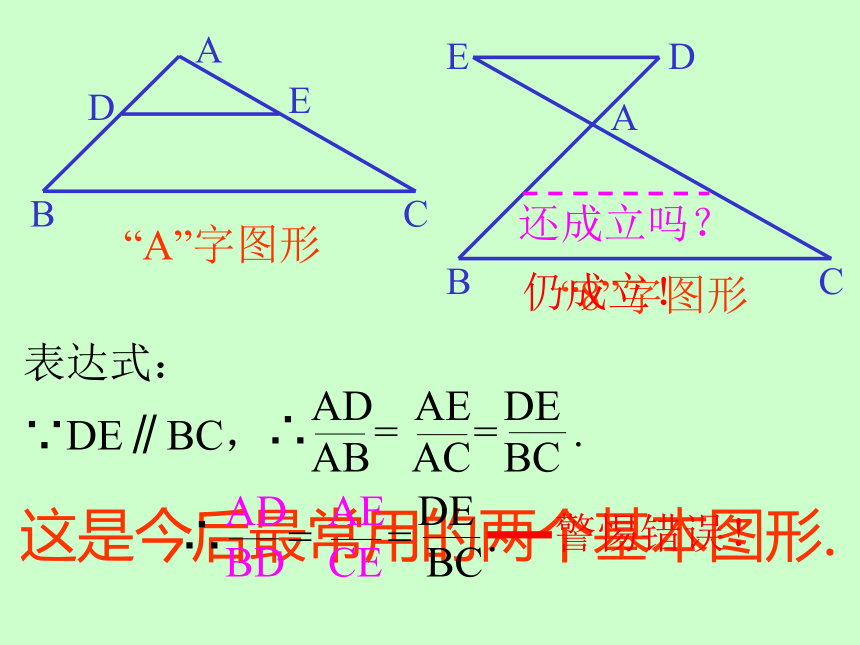
“A”字图形
“8”字图形
表达式：
∵DE∥BC，
这是今后最常用的两个基本图形.
D
A
B
C
E
D
A
B
C
E
∴ = = .
AD AE DE
AB AC BC
∴ = = .
AD AE DE
BD CE BC
警惕错误！
还成立吗？
仍成立！
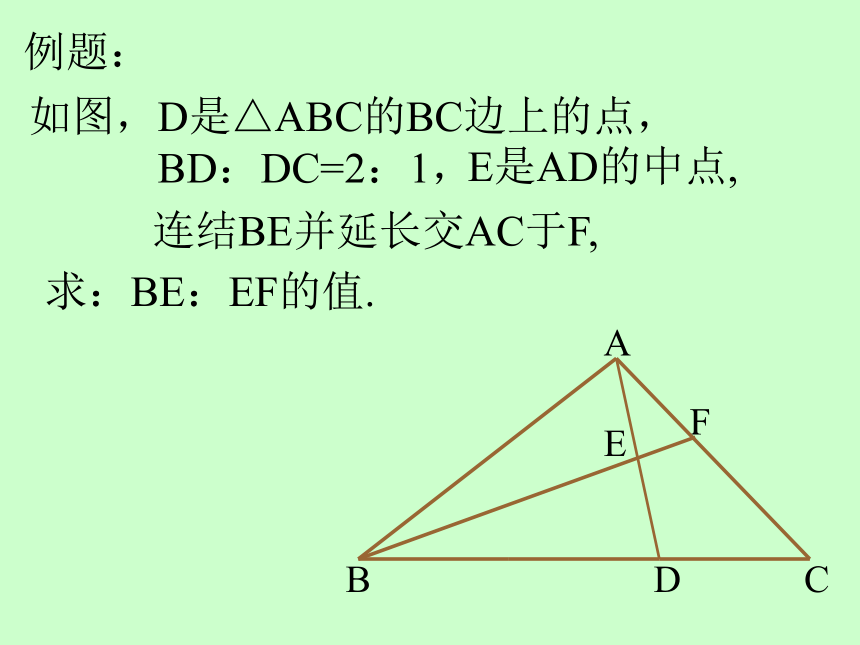
例题：
如图，D是△ABC的BC边上的点，
BD：DC=2：1，
求：BE：EF的值.
D
A
B
C
E
F
E是AD的中点,
连结BE并延长交AC于F,
D
A
B
C
E
F
G
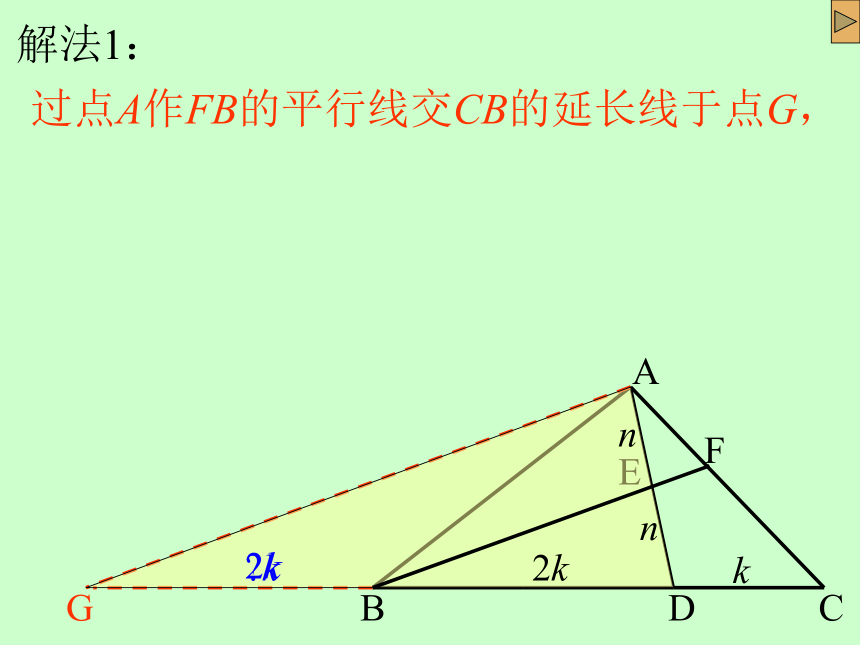
解法1：
k
k
2k
n
n
2k
过点A作FB的平行线交CB的延长线于点G，
D
A
B
C
E
F
G
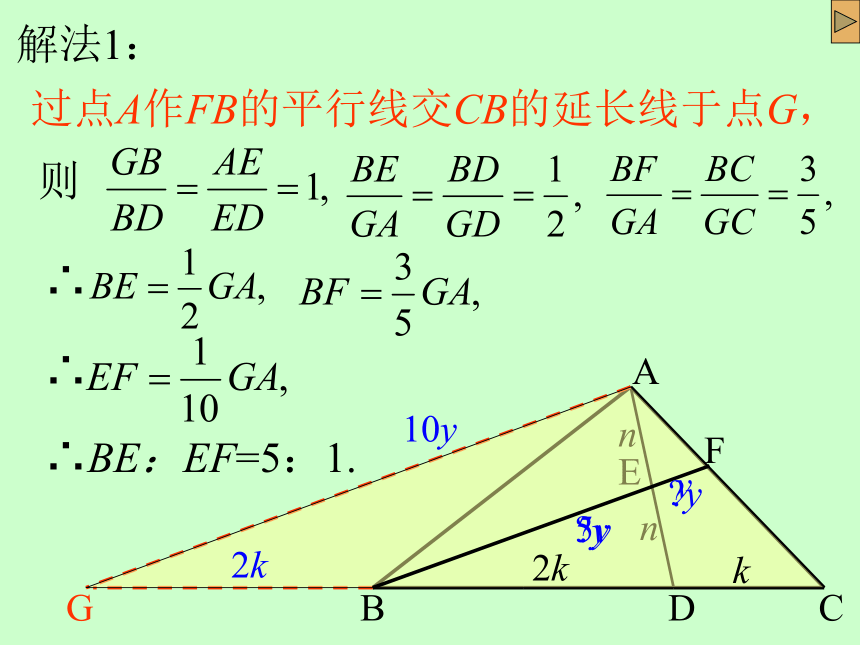
解法1：
过点A作FB的平行线交CB的延长线于点G，
n
n
10y
y
y
5y
2k
k
2k
则
∴
∴
∴BE：EF=5：1.
y
D
A
B
C
E
F
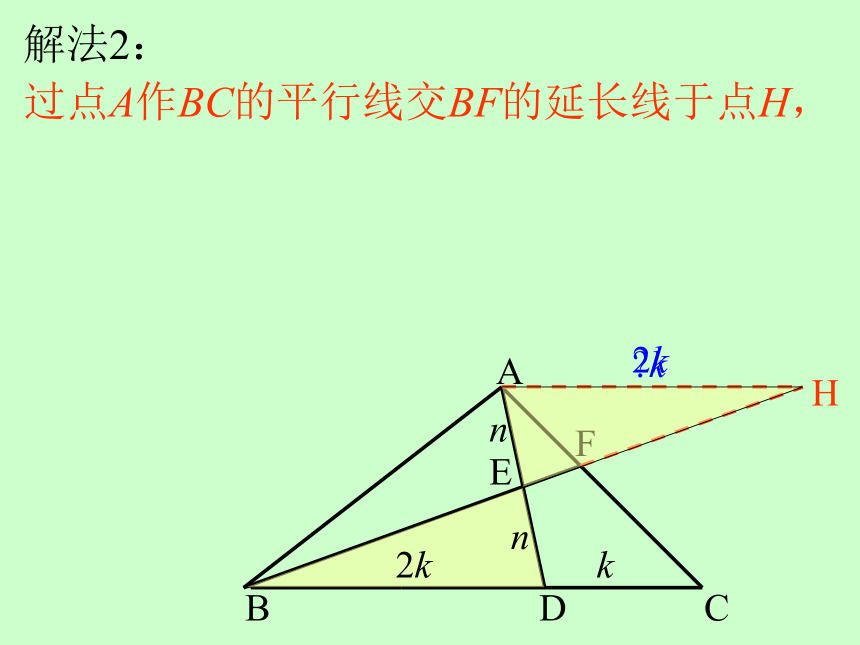
解法2：
过点A作BC的平行线交BF的延长线于点H，
H
k
n
k
2k
2k
n
D
A
B
C
E
F
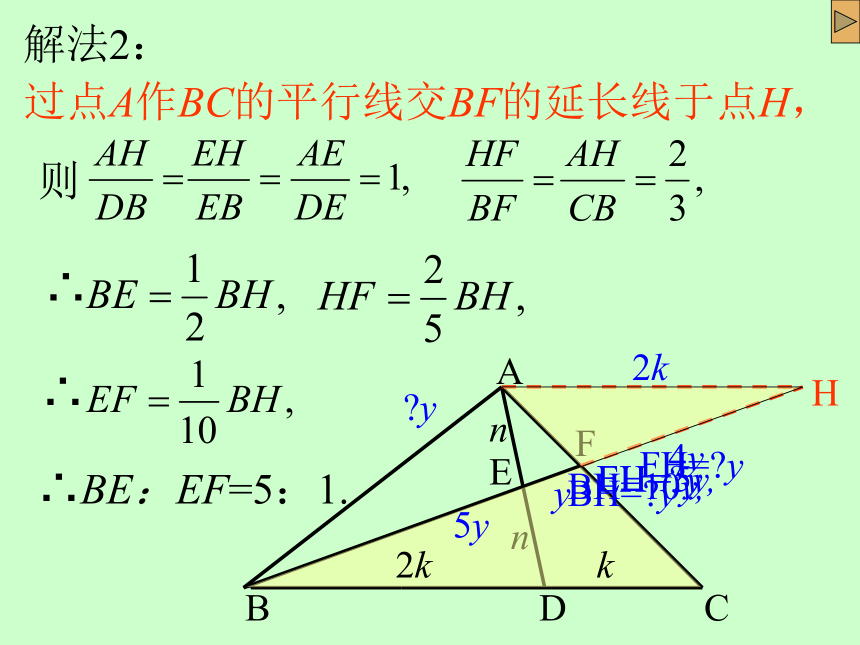
解法2：
过点A作BC的平行线交BF的延长线于点H，
H
n
2k
n
k
2k
y
4y
5y
y
∴BE：EF=5：1.
则
∴
∴
EH= y
EH=5y,
BH= y
BH=10y,
FH= y
D
A
B
C
E
F
N
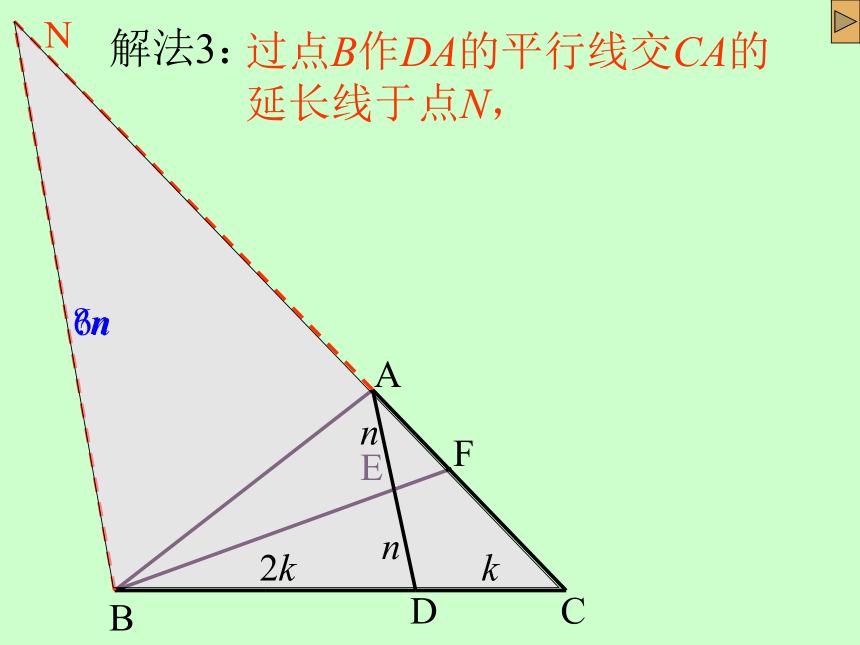
解法3：
过点B作DA的平行线交CA的延长线于点N，
n
6n
n
n
2k
k
D
A
B
C
E
F
N
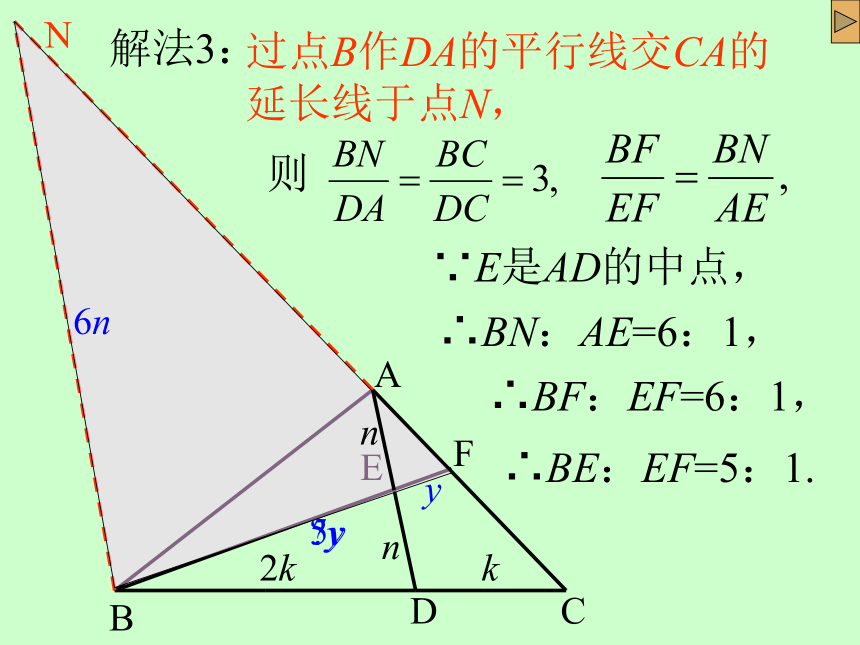
解法3：
过点B作DA的平行线交CA的延长线于点N，
n
2k
k
y
5y
y
6n
n
∴BE：EF=5：1.
则
∵E是AD的中点，
∴BF：EF=6：1，
∴BN：AE=6：1，
D
A
B
C
E
F
解法4：
M
过点B作AC的平行线交AD的延长线于点M，
n
n
2k
k
n
4n
D
A
B
C
E
F
解法4：
M
过点B作AC的平行线交AD的延长线于点M，
n
n
2k
k
4n
y
5y
y
∴BE：EF=5：1.
∴MD=2AD，
又BE：EF=ME：AE，
则
于是 ME=5AE，
D
A
B
C
E
F
解法5：
过点C作DA的平行线交BF的延长线于点I，
I
2p
p
3p
2k
k
2p
D
A
B
C
E
F
解法5：
过点C作DA的平行线交BF的延长线于点I，
I
2k
k
2p
2x
2p
3p
x
3x
D
A
B
C
E
F
解法5：
过点C作DA的平行线交BF的延长线于点I，
I
2k
k
2p
2p
3p
x
10x
2x
3x
则
即
∴
又
∴BE：EF=5：1.
D
A
B
C
E
F
解法6：
过点C作FB的平行线交AD的延长线于点J，
J
2p
p
p
2k
2p
k
D
A
B
C
E
F
解法6：
过点C作FB的平行线交AD的延长线于点J，
J
2p
x
p
5x
2k
2p
k
2x
D
A
B
C
E
F
解法6：
过点C作FB的平行线交AD的延长线于点J，
J
2p
p
5x
2k
2p
k
2x
x
10x
则
∴ED=2JD，
BE=2JC,
∴BE：EF=5：1.
D
A
B
C
E
F
n
2k
k
解法7：
过点D作CA的平行线交BF于点P，
P
y
y
n
y
D
A
B
C
E
F
n
解法7：
过点D作CA的平行线交BF于点P，
P
n
2k
k
y
y
4y
y
∴BE：EF=5：1.
则
∴PE=EF=
PF，
∴
BP=2PF，
D
A
B
C
E
F
n
n
2k
解法8：
过点D作BF的平行线交AC于点Q，
y
k
Q
y
2y
D
A
B
C
E
F
n
n
解法8：
过点D作BF的平行线交AC于点Q，
Q
2k
k
y
2y
5y
y
∴BE：EF=5：1.
∴
D
A
B
C
E
F
2k
解法9：
过点E作BC的平行线交AC于点S，
S
n
n
k
k
D
A
B
C
E
F
解法9：
过点E作BC的平行线交AC于点S，
S
n
n
y
5y
y
2k
k
∴BE：EF=5：1.
∴
∵BC=3DC，
∴BF：EF=6：1，
D
A
B
C
E
F
n
n
2k
解法10：
过点E作AC的平行线交BC于点T，
T
k
k
D
A
B
C
E
F
n
n
2k
解法10：
过点E作AC的平行线交BC于点T，
T
y
y
5y
∵BD=2DC，
∴
∴BE：EF=5：1.
D
A
B
C
F
n
2k
解法11：
Z
过点F作BC的平行线交AD于点Z，
设EF=1，BE=x，
在△ZEF和△DEB中，有
E
n
k
D
A
B
C
F
n
2k
解法11：
Z
过点F作BC的平行线交AD于点Z，
设EF=1，BE=x，
在△ZEF和△DEB中，有
E
n
在△ADC中，有
k
D
A
B
C
F
n
2k
解法11：
Z
过点F作BC的平行线交AD于点Z，
设EF=1，BE=x，
在△ZEF和△DEB中，有
E
n
在△ADC中，有
k
D
A
B
C
F
n
2k
解法11：
Z
过点F作BC的平行线交AD于点Z，
设EF=1，BE=x，
在△ZEF和△DEB中，有
E
n
在△ADC中，有
k
D
A
B
C
F
n
2k
解法11：
Z
在△ZEF和△DEB中，有
∴BE：EF=5：1.
E
n
k
D
A
B
C
E
F
n
2k
解法12：
过点F作AD的平行线交BC于点Y，
Y
设EF=1，BE=x，
在△BFY中，有
n
D
A
B
C
E
F
2k
解法12：
Y
在△ADC中，有
n
n
过点F作AD的平行线交BC于点Y，
设EF=1，BE=x，
在△BFY中，有
D
A
B
C
E
F
2k
解法12：
Y
n
n
D
A
B
C
E
F
2k
解法12：
Y
n
n
在△BFY中，有
∴BE：EF=5：1.
A
B
C
D
E
F
P
y
2k
2n
n
k
2y
6y
A
B
C
D
E
F
P
y
2k
3n
n
k
3y
8y
A
B
C
D
E
F
P
y
2k
4n
n
k
4y
10y
A
B
C
D
E
F
P
y
2k
mn
n
k
my
2my+2y
P
y
y
6y
D
A
B
C
F
n
3k
E
n
k
P
y
y
8y
D
A
B
C
F
n
4k
E
n
k
P
y
y
10y
D
A
B
C
F
n
5k
E
n
k
P
y
y
2my
D
A
B
C
F
n
mk
E
n
k
A
B
C
D
E
F
P
y
hk
mn
n
k
my
hmy+hy
}
练习题目：
如图，D是△ABC的BC边上的点，
BD：DC=2：1，
求AF：CF的值.
D
A
B
C
E
F
E是AD的中点,
连结BE并延长交AC于F,
D
A
B
C
E
F
I
解法1：
过点A作FB的平行线交CB的延长线于点I，
2k
n
n
2k
k
2x
3x
AF：CF=2：3.
D
A
B
C
E
F
解法2：
过点A作BC的平行线交BF的延长线于点J，
J
2k
n
n
2k
k
2x
3x
AF：CF=2：3.
D
A
B
C
E
F
n
n
2k
k
解法3：
M
4n
过点B作AC的平行线交AD的延长线于点M.
2x
10x
3x
AF：CF=2：3.
D
A
B
C
E
F
N
解法4：
过点B作DA的平行线交CA的延长线于点N，
2k
k
n
n
6n
2x
10x
3x
AF：CF=2：3.
D
A
B
C
E
F
解法5：
过点C作DA的平行线交BF的延长线于点G，
G
2k
k
2p
3p
2p
2x
3x
AF：CF=2：3.
D
A
B
C
E
F
解法6：
过点C作FB的平行线交AD的延长线于点H，
H
2k
k
2p
p
2p
2x
3x
AF：CF=2：3.
D
A
B
C
E
F
解法7：
过点D作CA的平行线交BF于点P，
P
n
n
2x
2x
2k
k
3x
AF：CF=2：3.
D
A
B
C
E
F
解法8：
过点D作BF的平行线交AC于点Q，
Q
n
n
2x
2x
2k
k
x
AF：CF=2：3.
D
A
B
C
E
F
解法9：
过点E作BC的平行线交AC于点S，
S
n
n
h
2h
4h
y
5y
4y
AF：CF=2：3.
D
A
B
C
E
F
解法10：
过点E作AC的平行线交BC于点T，
T
n
n
h
h
4h
5y
6y
4y
AF：CF=2：3.
D
A
B
C
E
F
解法11：
过点F作AD的平行线交BC于点Y，
Y
n
n
2k
1
x
设CF=1，AF=x，
D
A
B
C
E
F
解法11：
过点F作AD的平行线交BC于点Y，
Y
n
1
x
设CF=1，AF=x，
n
2k
AF：CF=2：3.
D
A
B
C
E
F
解法12：
过点F作BC的平行线交AD于点Z，
Z
n
n
2k
1
x
设CF=1，AF=x，
D
A
B
C
E
F
解法12：
过点F作BC的平行线交AD于点Z，
Z
n
1
x
设CF=1，AF=x，
n
2k
AF：CF=2：3.
本课小结：
在解这类习题时，要在熟悉基本图形的
通过两道习题的各12种解法，充分说明
作平行线转移两条线段的比的方法和两个基
做这类习题时的机会多多。
本图形在解题时的应用，解法的多样性说明
基础上，选择最简捷的方法。
用者须知：
过例题中每一个点均可作两条辅助线，
得到两种不同的解法。课件中依辅助线的作
法，按“先左后右，先上后下”的顺序排列。
如果学生提出的作法是“右”或“下”，则可使
用动作按钮到达该图，这种方法完成后再用
动作按钮回到“左”或“上”，完成后再到下一
个点的讨论。
鼠标移过彩图时可出现变色，以突出基
本图形。