等腰三角形 课件

(共19张PPT)
等腰三角形
A
B
C
有两条边相等
的三角形
A
B
C
一、复习引入：
1、什么是等腰三角形？
2、用尺规作一个等腰三角形，测量它
的两底角，它们相等吗？
1、掌握等腰三角形的性质定理及推论。
2、理解定理的证明及所用数学方法。
3、了解等腰三角形和等边三角形的
从属关系，能说出等边三角形的有关性质。
4、能运用等腰三角形的性质进行简单的论证和计算。
5、养成仔细观察认真分析的良好学习习惯。
二、教学目标：
A
B
C
三、等腰三角形的性质：
A
B
C
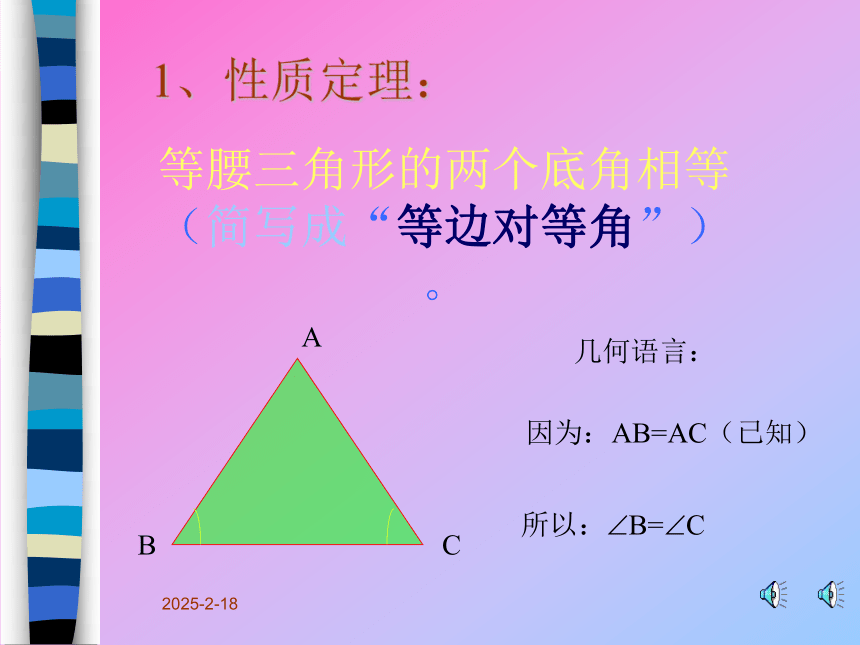
几何语言：
因为：AB=AC（已知）
所以： B= C
1、性质定理：
等腰三角形的两个底角相等
（简写成“等边对等角”）。
A
B
D
C
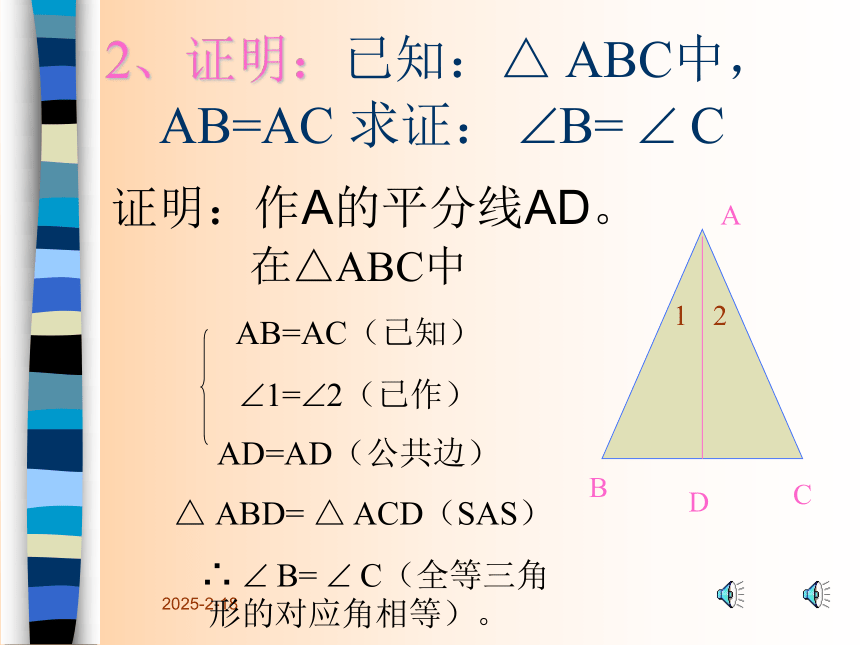
在△ABC中
AB=AC（已知）
1= 2（已作）
AD=AD（公共边）
△ ABD= △ ACD（SAS）
∴ B= C（全等三角形的对应角相等）。
1
2
2、证明：已知：△ ABC中，
AB=AC 求证： B= C
证明：作A的平分线AD。
练习1：
还有其它辅助线作法吗？讨论一下，看谁能想出更好的办法？
A
B
C
D
作△ABC的高AD：
∴在Rt△ABD和Rt△ACD中：
AB=AC（已知）
　AD=AD（公共边）
Rt△ABD≌Rt△ACD（HL）　∴∠B=∠C（全等三角形的对应角相等）。
作高：
A
B
C
D
作中线：
作底边BC的中线AD，
则BD=CD
在△ABD和△ACD中：
AB=AC（已知）
BD=CD（已作）
AD=AD（公共边）
∴△ABD≌△ACD（SSS）
∴∠B=∠C
（全等三角形的对应角相等）
练习2：
1、等腰三角形的一个底角等于75度，
那么它的顶角等于多少度？
2、等腰直角三角形的每一个锐角等
于多少度？
3、等腰直角三角形斜边上的高把直
角分成两个角，求这两个角的度数。
A
B
C
D
1
2
∵AB=AC（已知）
∠1=∠2 （已知）
∴AD⊥BC
BD=CD（推论1）
几何语言
3、推论：
推论1：
等腰三角形顶角的平分线平分
底边并且垂直于底边。
A
B
C
D
三线合一：
等腰三角形的顶角平分线，
底边上的中线，高互相重合。
A
B
C
推论2：
等边三角形的各角都相等，
并且每一个角都等于60度。
A
B
C
练习3：
已知：△ABC是等边三角形，
AD是高，说出的∠BAC；
∠BAD；∠B；∠C度数。
A
B
D
C
解： 在△ABC中，
∵AB=AC（已知），
∴∠B=∠C（等边对等角）。
∴∠B=∠C=1/2（180-∠BAC）=40度
又∵AD⊥BC（已知），
∴∠BAD=∠CAD（推论1），
∴∠BAD=∠CAD=50度。
4、例题1：
已知：房屋的顶角∠BAC=100度，过房顶A 的立柱AD⊥BC，房椽AB=AC，求顶架上∠B，∠C，∠BAD，∠CAD的度数？
四、小结：这节课我们学了哪些内容？
等腰三角形
1、性质定理
2、推论
（1）推论1
（三线合一）
（2）推论2
五、达标检测：
1、判断：
（1）在等腰三角形中，有一个角是84度，则这个角必定是顶角（ ）；
（2）等腰直角三角形斜边上的中线与斜边上的高重合（ ）；
（3）等边三角形任一个角的平分线都垂直平分这个角的对边（ ）。
2、填空：
（1）等腰三角形的两内角比是1：4，则底角度数为——。
（2）△ABC中，AB=AC，AD是BC边上的高，∠BAD=75度，则∠BAC=——度，∠B=——度。
30或80
150
15
×
√
√
六、作业：P72 第3、5题