等腰三角形的复习 课件

(共26张PPT)
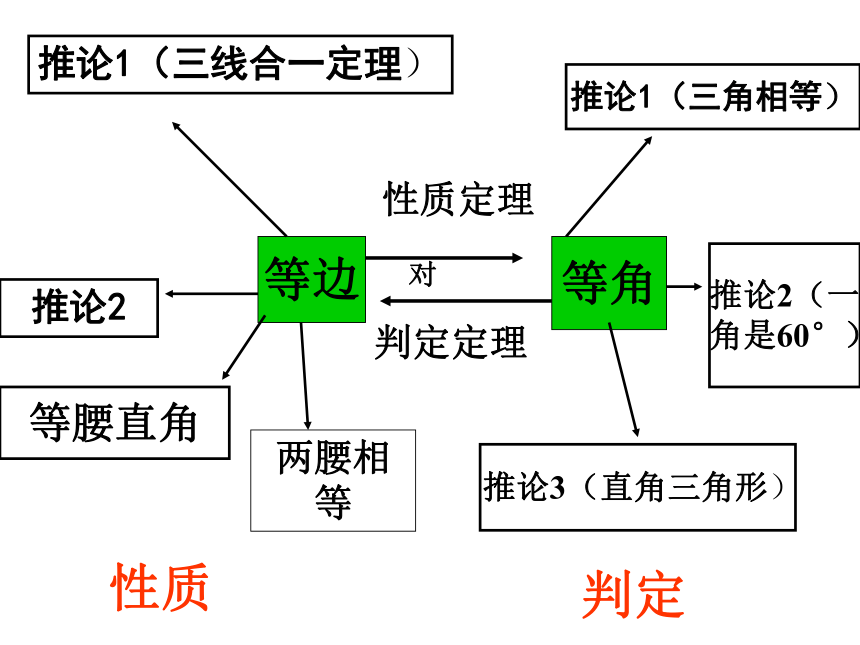
等腰三角形的复习
等边
等角
对
性质定理
判定定理
推论1（三线合一定理）
推论2
等腰直角
推论1（三角相等）
推论2（一
角是60°）
推论3（直角三角形）
性质
判定
两腰相等
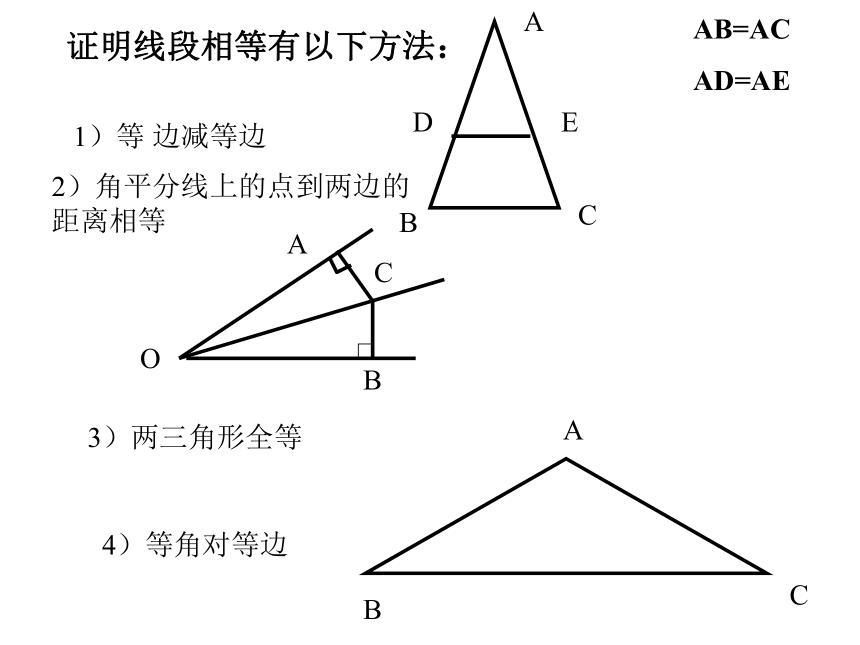
证明线段相等有以下方法：
1）等 边减等边
A
B
C
D
E
2）角平分线上的点到两边的距离相等
O
A
B
C
3）两三角形全等
4）等角对等边
A
B
C
AB=AC
AD=AE
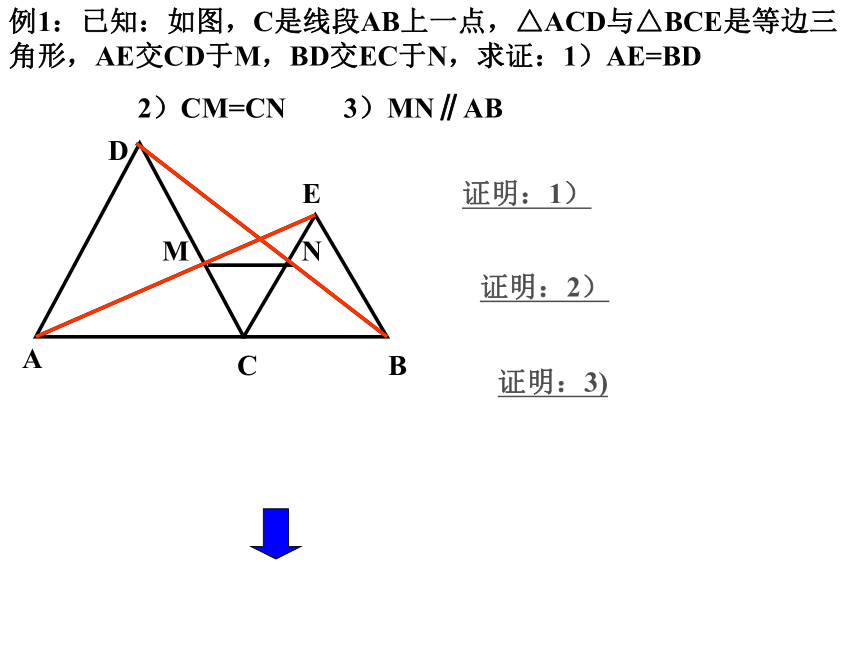
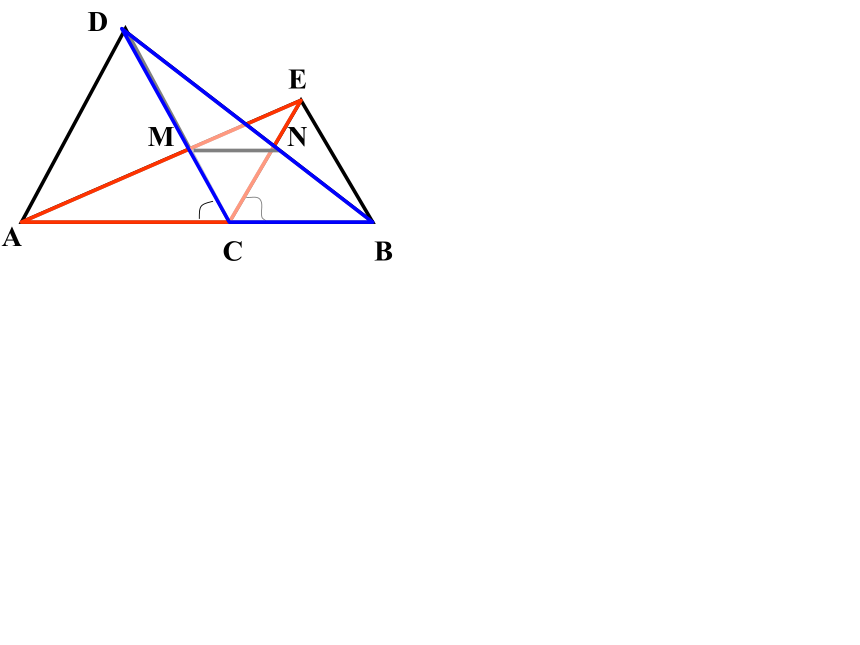
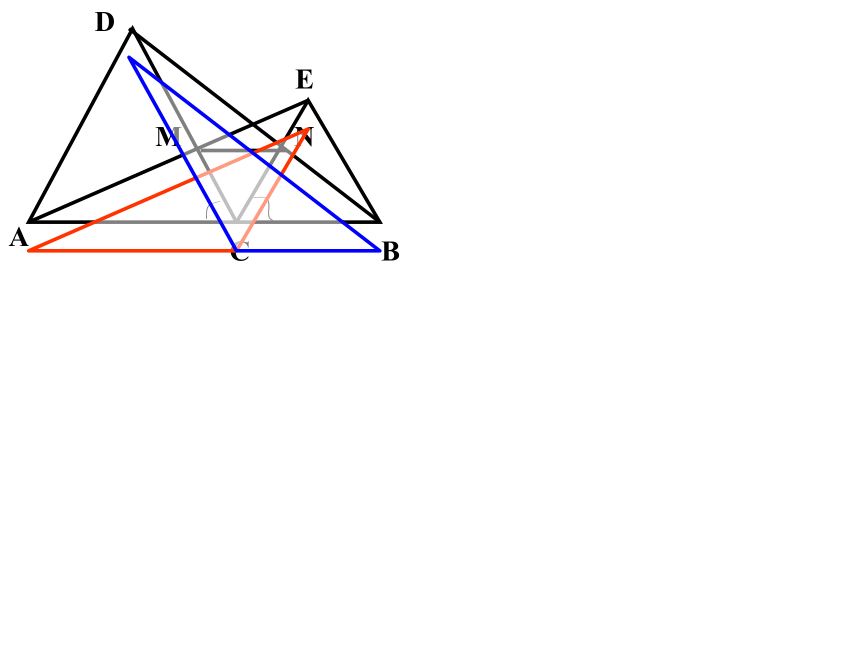
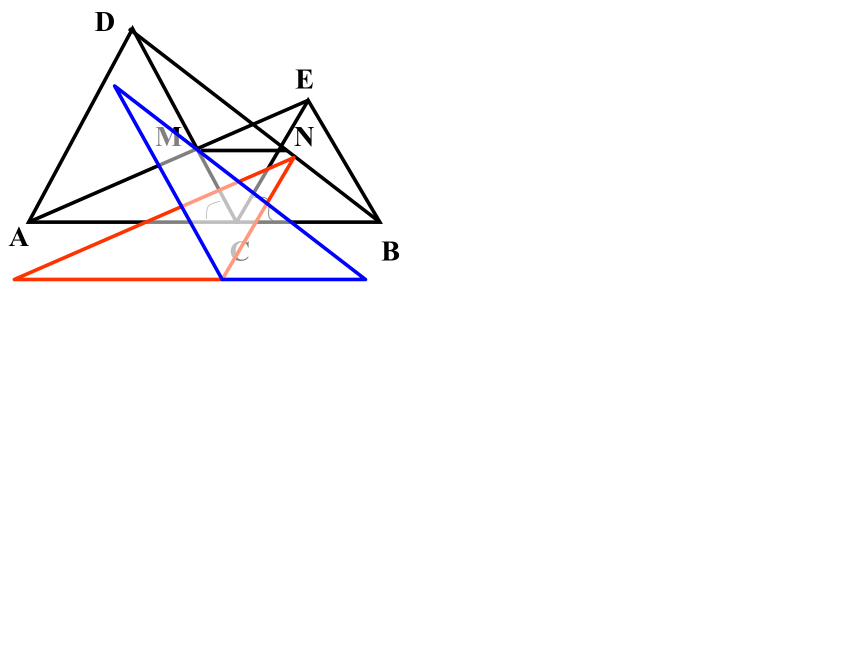
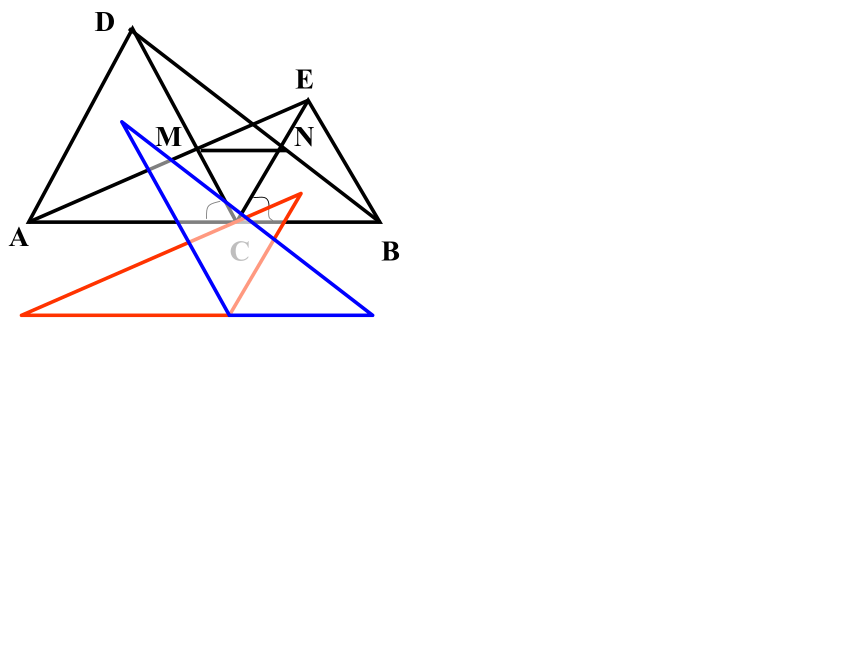
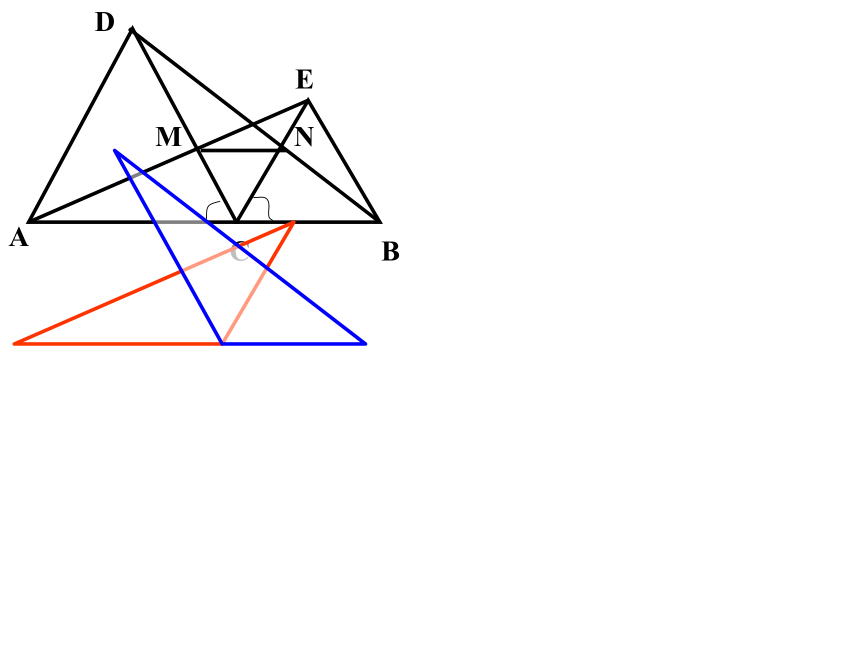
例1：已知：如图，C是线段AB上一点，△ACD与△BCE是等边三角形，AE交CD于M，BD交EC于N，求证：1）AE=BD
2）CM=CN 3）MN∥AB
A
B
C
D
E
M
N
证明：1）
证明：2）
证明：3)
B
C
E
M
N
D
A
B
C
E
M
N
D
A
B
C
E
M
N
D
A
B
C
E
M
N
D
A
B
C
E
M
N
D
A
B
C
E
M
N
D
A
B
C
E
M
N
D
A
B
C
E
M
N
D
A
B
C
E
M
N
D
A
证明：1）∵△ACD与△BCE是等边三角形（已知）
∴CE=CB，AC=DC（等边三角形的定义）
∠DCA= ∠ECB=60°（等边三角形三角都相等）
∴ ∠DCA+ ∠DCE= ∠DCE+ECB
即∠ACE= ∠DCB
在△ACE和△DCB中
AC=DC（已证）
∠ACE= ∠DCB（已证）
CE=CB（已证）
∴△ACE≌△DCB（SAS）
∴AE=BD（全等三角形对应边相等）
A
C
B
D
E
C
E
M
N
D
A
B
C
E
M
N
D
A
B
C
E
M
N
D
A
B
C
E
M
N
D
A
B
C
E
M
N
D
A
B
C
E
M
N
D
A
B
C
E
M
N
D
A
B
C
E
M
N
D
A
B
C
E
M
N
D
A
B
证明：∵△ACE≌△DCB（已证）
∴ ∠CAM= ∠CDN（全等三角形对应角相等）
∵ ∠DCA= ∠ECB=60°（已证）
∴ ∠MCN=180°-60°-60°= 60°（平角的定义）
∴ ∠DCA= ∠MCN=60°
在△ACM和△DCN中
∠CAM= ∠CDN（已证）
AC=DC（已证）
∠ACM= ∠MCN（已证）
∴△ACM≌△DCN（ASA）
∴ CM=CN（全等三角形对应角相等）
D
A
C
M
N
已证： △ACE≌△DCB，已知两个等边三角形
C
E
M
N
D
A
证明：∵CM=CN， ∠MCN=60°（已证）
∴△CMN是等边三角形（有一个角为60°
的等腰三角形是等边三角形）
∴ ∠MNC=60°（等边三角形的各角为60°）
∴ ∠ECB= ∠MNC=60°
∴MN∥AB（内错角相等两直线平行）
B
A
C
B
M
N
60°
60°
已证：∠ACM= ∠BCN= ∠MCN=60°
CM=CN
练习：已知：如图，△ABD和△ACE是等腰直角三角形∠DAB和∠EAC是直角，求证：①DC=BE
②DC⊥BE
D
B
C
A
E
O
D
B
C
A
E
O
△ABD和△ACE是等腰直角三角形
证明：∵△ABD和△ACE是等腰直角三角形（已知）
∴AB=AD，AC=AE
∠BAD= ∠CAE=90°（ 等腰直角三角形的定义）
∴ ∠BAD+ ∠BAC= ∠CAE+ ∠BAC即∠DAC= ∠BAE
在△ACD和△AEB中
AD=AB（已证）
∠DAC= ∠BAE（已证）
AC=AE（已证）
∴△ACD≌△AEB（SAS）
∴CD=BE（全等三角形对应边相等）
D
B
C
A
E
O
O
F
△ACD≌△AEB
证明：∵ △ACD≌△AEB（已证）
∴ ∠ACD= ∠AEB
∵ ∠AFE= ∠OFC（对顶角相等）
又∵ ∠AFE+ ∠AEF=90°
（直角三角形的两锐角互余）
∴ ∠OFC+ ∠ACD=90°（等量代换）
∵ ∠COF=180°-（ ∠OFC+ ∠ACD）=180°-90°=90°（三角形的内角和定理）
∴CD⊥BE（垂直的定义）
谢谢指导