等腰三角形的性质 课件

(共10张PPT)
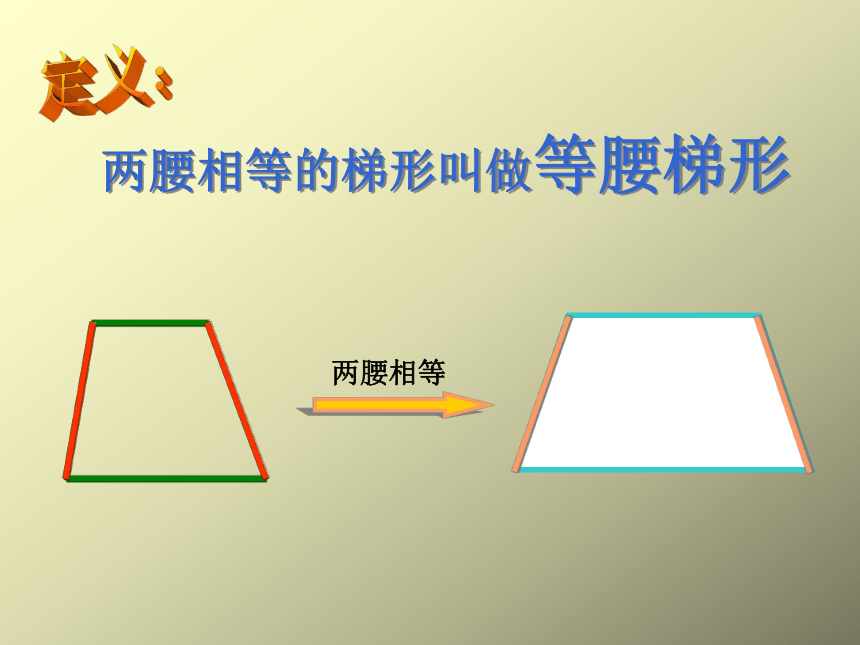
等腰梯形及其性质
两腰相等的梯形叫做等腰梯形
两腰相等
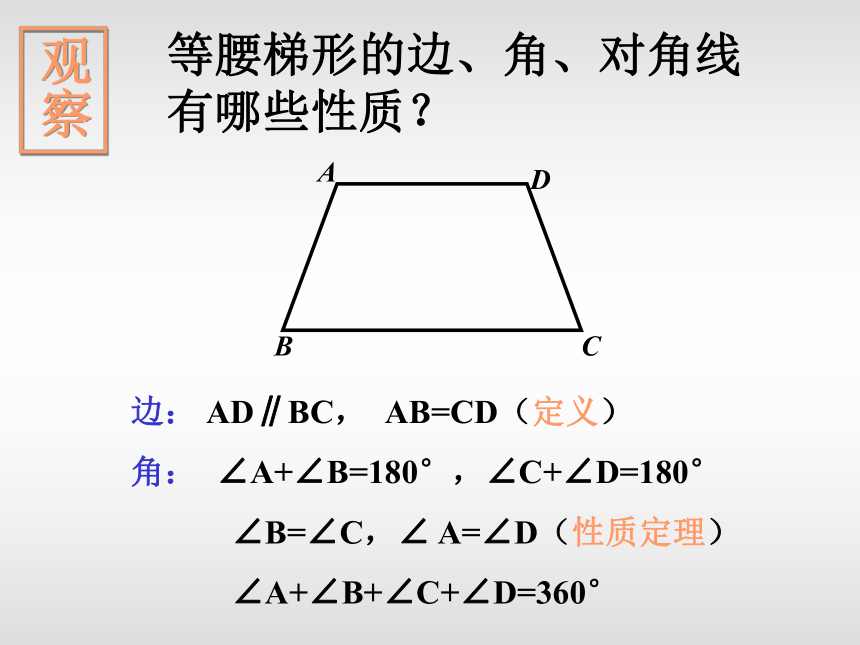
等腰梯形的边、角、对角线
有哪些性质？
A
B
C
D
观察
边： AD∥BC， AB=CD（定义）
角： ∠A+∠B=180°，∠C+∠D=180°
　　　∠B=∠C，∠ A=∠D（性质定理）
　　　∠A+∠B+∠C+∠D=360°
C
E
已知： 梯形ABCD中，
AD∥BC，AB=CD
求证：∠B=∠C
求证：等腰梯形在同一底上的两个角
相等
A
D
B
∵AD∥BC，AE∥CD
∴CD=AE
∴AB=DC
∴AE=AB
∴∠1=∠B
∵∠1=∠C
∴∠B=∠C
(
1
证明： 过点A作AE∥CD，
交BC于点E
等腰梯形的边、角、对角线
有哪些性质？
观察
边： AD∥BC， AB=CD（定义）
角： ∠A+∠B=180°，∠C+∠D=180°
　　　∠B=∠C ∠ A=∠D（性质定理）
　　　∠A+∠B+∠C+∠D=360°
A
B
C
D
对角线：AC=BD（性质定理）
已知：如图，在梯形ABCD中， AD∥BC，AB=CD 求证：AC=DB
求证：等腰梯形两条对角线相等
A
B
C
D
证明：在梯形ABCD中，
∵AB=DC，
∴∠ABC=∠DCB（等腰梯形在同一底上的两个角相等）.
又 BC=CB,
∴ △ABC≌△DCB.
∴AC=DB.
已知: 如图,在等腰梯形ABCD中，AD∥BC，
AB=CD,BE平分∠ABC交AD于E，且
AE=ED
问：（1）图中有几个等腰三角形，并指出。
（2）图中边、角存在哪些特殊关系。
A
B
C
D
E
解：1）有3 个等腰三角形，
分别是△ABE、△DCE、△EBC。
(
(
(
(
(
(
1
2
3
4
5
6
2) 边：
AB=AE=ED=DC;
BE=CE;
AD=AB+CD
角：
∠1=∠2=∠3=∠4=∠5=∠6;
∠A=∠D=∠BEC.
研究
已知: 如图,在等腰梯形ABCD中，AD∥BC，
AB=CD,BE平分∠ABC交AD于E，且
AE=ED
问：（3）∠A是否是定值？如果是，请求出其值；
　 如果不是， 请说明理由。
A
B
C
D
E
(
(
(
(
(
(
1
2
3
4
5
6
研究
B
C
A
D
1 熟练掌握等腰梯形及 其性质。
2 常通过辅助线来研究
等腰梯形。
作业
1、继续思考用怎样的辅助线， 可以
在等腰梯形中划出等腰三角形。
2、课本第179页 2、3题。