2.1等腰三角形

(共21张PPT)
等 腰 三 角 形
请您欣赏
请您欣赏
任 何 数 学 分 枝，无 论 怎 样 抽 象，总 有 一 天 可 被 应 用 于 现 实 世 界 的 各 种 现 象
-------尼 古拉
腰
等 腰 三 角 形
一 基本概念
1 等腰三角形：有两边相等的三角形。
2 分类 （1）只有两边相等的三角形
（2）三边都相等的三角形
（等边三角形）
腰
腰
腰
底边
底边
腰=底边
底角
底角
顶角
底角
底角
顶角
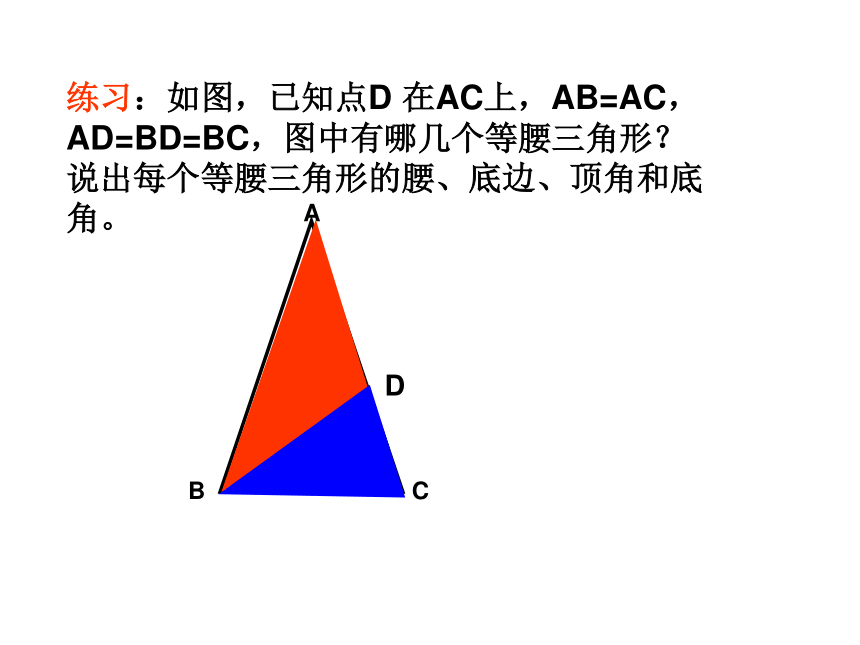
练习：如图，已知点D 在AC上，AB=AC， AD=BD=BC，图中有哪几个等腰三角形？ 说出每个等腰三角形的腰、底边、顶角和底 角。
A
B
C
D
例1 等腰三角形的一边长为4，另一边长为6，问
可组成几种不同的等腰三角形？（一边长为
3，另一边长为6呢）
解：当取腰长为4，则三角形三边为4，4，6
当取腰长为6，则三角形三边为6，6，4
（满足三角形三边关系）
（满足三角形三边关系）
所以可组成2种不同的三角形。
当取腰长为3，则三边3，3，6
（不满足三角形三边关系）
当取腰长为6，则三边6，6，3
（满足三角形三边关系）
所以可组成1种三角形
变式1：一个等腰三角形周长为21，其中一 边长为9
求三角形的腰长？
解：当边长9为腰长，则三角形三边9，9，3
当边长9为底边长，则三角形三边6，6，9
（满足三边关系）
（满足三边关系）
所以三角形 的腰长为 9或6。
变式2：已知等腰三角形的底边和一腰长是方程组
X+2Y=4
3X+Y=7 的解，求这个三角形的各边长
解：解方程组得：Ｘ＝２，Ｙ＝１
当取腰长为２，则三角形三边２，２，１
（满足三角形三边要求）
　
当取腰长为１，则三角形三边１，１，２
（不满足三角形三边）
所以这个三角形的边为２，２，１
变式３：已知等腰三角形一腰上的中线将三角形周
　　　　长分成２：１两部分，已知三角形底边长
　　　　为５，求腰长？
解：如图，令ＣＤ＝Ｘ，则ＡＤ＝Ｘ，ＡＢ＝２Ｘ
∵底边ＢＣ＝５
∴ＢＣ＋ＣＤ＝５＋Ｘ
　ＡＢ＋ＡＤ＝３Ｘ
∴（５＋Ｘ）：３Ｘ＝２：１
　或３Ｘ：（５＋Ｘ）＝２：１
得Ｘ＝１或Ｘ＝１０
即腰长为２或２０
2不合题意，所以腰长为20
Ａ
Ｂ
Ｃ
Ｄ
X
X
2X
5
例2:已知,如图,AB,AD是等腰ΔABD的两腰,AC平
分∠BAD,求证:ΔBCD是等腰三角形
A
B
C
D
在ΔABC与ΔADC中,
AB=AD(等腰三角形的两腰)
∠BAC= ∠DAC(已证)
AC=AC(公共边)
证明:∵ AC平分∠BAD,
∴ ∠BAC= ∠DAC
∴ ΔABC≌ΔADC(SAS)
∴BC=DC(全等三角形对应边相等)
∴ΔBCD是等腰三角形(等腰三角形定义)
练习:已知, ∠1= ∠2, ∠3= ∠4
求证:, ΔABC是等腰三角形,
A
B
C
D
1
2
3
4
二 轴对称图形
概念:把一个图形沿着一条直线折过来,直线两旁
的部分能够相互重合,那么这个图形叫轴对称
图形,这条直线叫对称轴.
结论:等腰三角形的对称轴有一条或三条
练习:观察下列图形,每个图形是不是轴对称图形
如果是,说出他们的对称轴.
A
O
B
C
D
三 应用新知,挑战自我
说出下列从生活中提炼出的图形是否是轴对称图形,如果是,请判断他们各有几条对称轴
(投石入水)
(把握方向)
(天圆地方)
(对称轴:无数条)
(对称轴:3条)
(对称轴:4条)
小结: 1 等腰三角形的基本概念;
2 利用等腰三角形的三边关系,进行底边和腰长
之间的换算（分类归纳和方程思想）；
3 轴对称图形的基本概念和对称轴的确定,
纸上得来终觉浅
绝知此事须躬行