5.5平行四边形的判定1

(共11张PPT)
5.5 平行四边形的判定 （1）
龙游塔石初中 席燕琴
边
平行四边形的对边平行
并且相等
角
平行四边形的对角相等
对角线
平行四边形的对角线
互相平分
平行四边形的性质：
怎么判断一个四边形是平行四边形的？
定义：两组对边分别平行的四边形是平行四边形
5.5平行四边形的判定（1）
A
B
D
C
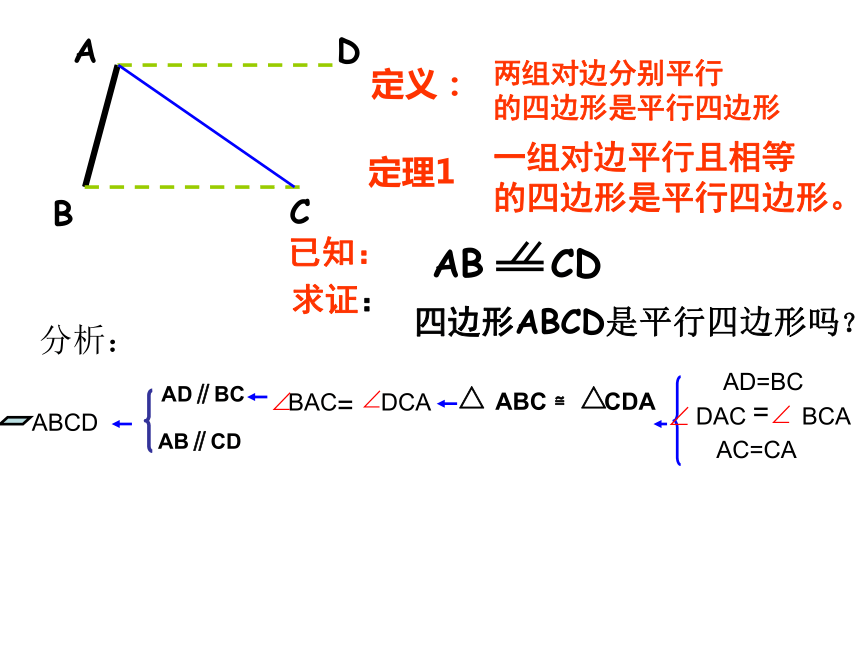
AB CD
四边形ABCD是平行四边形吗？
一组对边平行且相等
的四边形是平行四边形。
定理1
已知：
求证：
两组对边分别平行
的四边形是平行四边形
定义：
AD∥BC
AB∥CD
ABC ≌ CDA
△
△
ABCD
DCA
=
BAC
AD=BC
BCA
DAC
=
AC=CA
分析：
一组对边平行且相等
的四边形是平行四边形。
定理1
两组对边分别平行
的四边形是平行四边形
定义：
A
B
D
C
定理2
两组对边分别相等的
四边形是平行四边形
（1）一组对边平行，另一组对边相等的四边形是平行四边形（ ）
（2）有两组边分别相等的四边形是平行四边形（ ）
判断真假
假
假
C
A
B
D
一组对边平行且相等
的四边形是平行四边形。
定理1
两组对边分别平行
的四边形是平行四边形
定义：
定理2
两组对边分别相等的
四边形是平行四边形
B
A
C
D
（1）
（2）
（3）
怎么拼可以拼出平行四边形？
A
B
D
C
求证：ＥＦ∥ＡＤ∥ＢＣ
例 如图　　ＡＢＣＤ中，
Ｅ、Ｆ分别是ＡＢ、ＣＤ中点，
Ａ
Ｂ
Ｄ
Ｃ
Ｅ
Ｆ
分析：
∥
AD
BC
EF∥AD
AEFD
AE
DF
AB CD
∵四边形ABCD是平行四边形，
∴ AB CD
∵ E，F分别是ＡＢ、ＣＤ中点，
∴ AE DF
(一组对边平行且相等的四边形是平行四边形.)
AEFD
是平行四边形
∴
∴ EF ∥AD
∴ EF ∥ AD ∥ BC
证明：
练习1 已知：平行四边形ABCD中E，F分别是边AD，BC的中点
证明：∵四边形ABCD 是平行四边形
∴AD BC
∵ED=1/2AD BF=1/2BC
∴ED BF
∴四边形EBFD是平行四边形
（一组对边平行且相等的四边形是平行四边形）
∴EB=DF
大显身手
(1)求证：BE=DF
练习1 已知：平行四边形ABCD中E，F分别是边AD，BC的中点
G
H
（2）连接AF、EC分别交BE、DF 于点G、点H，你能得到哪些平行四边形？
（3）连接GH，你又能 得到哪些平行四边形？
(1)求证：BE=DF
大显身手
D
A
B
C
E
F
证明：
四边形ABCD是平行四边形
AB ∥ CD且AB=CD
BAE= DCF
AE=CF
BAE= CDF
AB=CD
ABE ≌ CDF(SAS)
BE=DF
四边形BFDE是平行四边形
在 A BE和 CDF中
同理可证：DE=BF
练习2、已知：E、F是平行四边形ABCD对角线AC上的两点，并且AE=CF。
求证：四边形BFDE是平行四边形
小结：平行四边形的三个判定方法：
从边看:
两组对边分别平行
两组对边分别相等
一组对边平行且相等
的四边形是平行四边形