2020-2021学年九年级数学华东师大版下册 26.2.3 二次函数y=a(x-h)2的图象与性质(培优卷)(word版含答案)
文档属性
| 名称 | 2020-2021学年九年级数学华东师大版下册 26.2.3 二次函数y=a(x-h)2的图象与性质(培优卷)(word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 401.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-18 00:00:00 | ||
图片预览

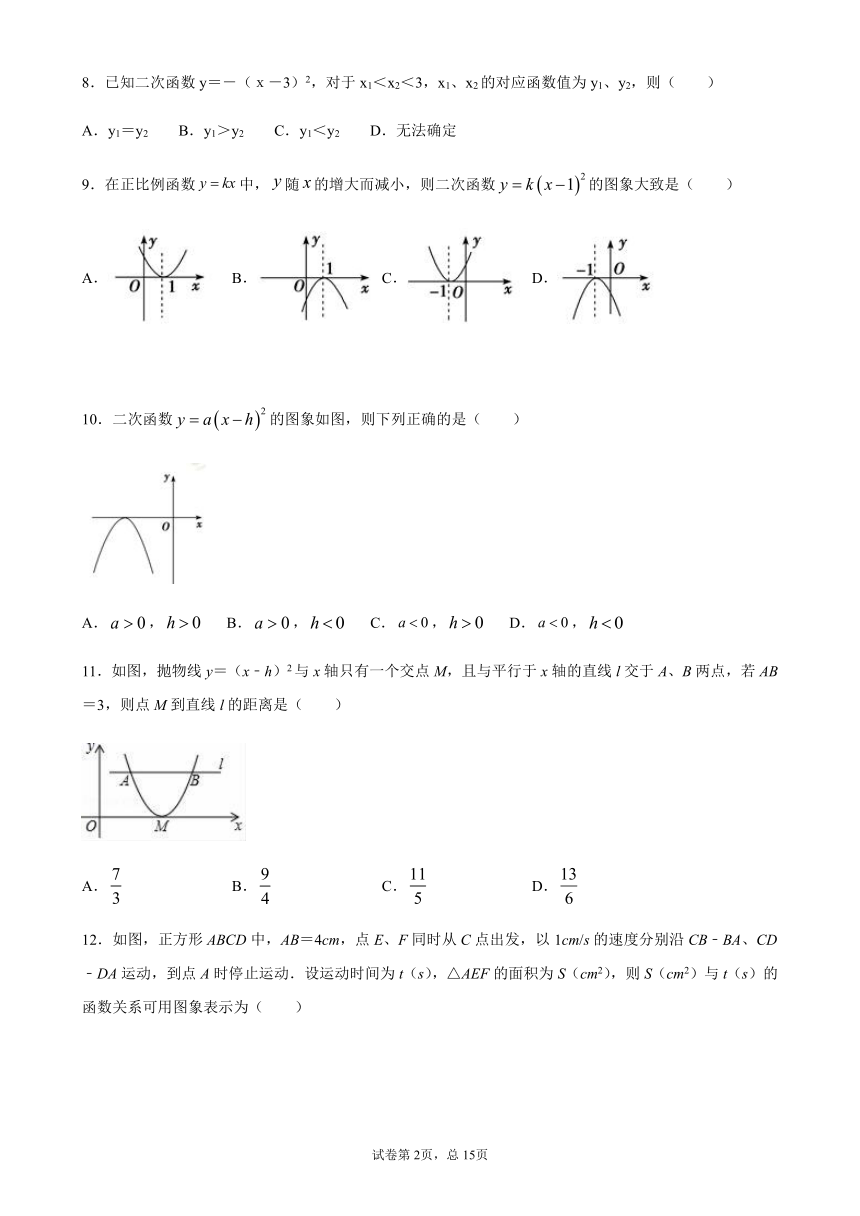


文档简介
26.2.3
二次函数y=a(x-h)2的图象与性质(培优卷)
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.已知抛物线的开口向下,则的取值范围是(
)
A.
B.
C.
D.
2.抛物线y=2(x-1)2的对称轴是(
)
A.1
B.直线x=1
C.直线x=2
D.直线x=-1
3.对于二次函数的图象,下列说法正确的是(
)
A.开口向上
B.对称轴是x=-3
C.当x>-4
时,y随x的增大而减小
D.顶点坐标为(-2,-3)
4.在抛物线上的一个点是(?
)
A.(2,3)
B.(-2,3)
C.(1,-2)
D.(0,-2)
5.已知二次函数,当时,随着的增大而增大,当时,随的增大而减小,当时,的值为(
)
A.2
B.
C.4
D.
6.抛物线y=﹣2(x﹣1)2的图象上有三个点A(﹣1,y1),B(1,y2),C(2,y3),则y1,y2,y3的大小关系是( )
A.>>
B.
>>
C.>>
D.
>>
7.顶点为,开口向下,开口的大小与函数的图象相同的抛物线所对应的函数是(
)
A.
B.
C.
D.
8.已知二次函数y=-(x-3)2,对于x1<x2<3,x1、x2的对应函数值为y1、y2,则(
)
A.y1=y2
B.y1>y2
C.y1<y2
D.无法确定
9.在正比例函数中,随的增大而减小,则二次函数的图象大致是(
)
A.
B.
C.
D.
10.二次函数的图象如图,则下列正确的是(
)
A.,
B.,
C.,
D.,
11.如图,抛物线y=(x﹣h)2与x轴只有一个交点M,且与平行于x轴的直线l交于A、B两点,若AB=3,则点M到直线l的距离是( )
A.
B.
C.
D.
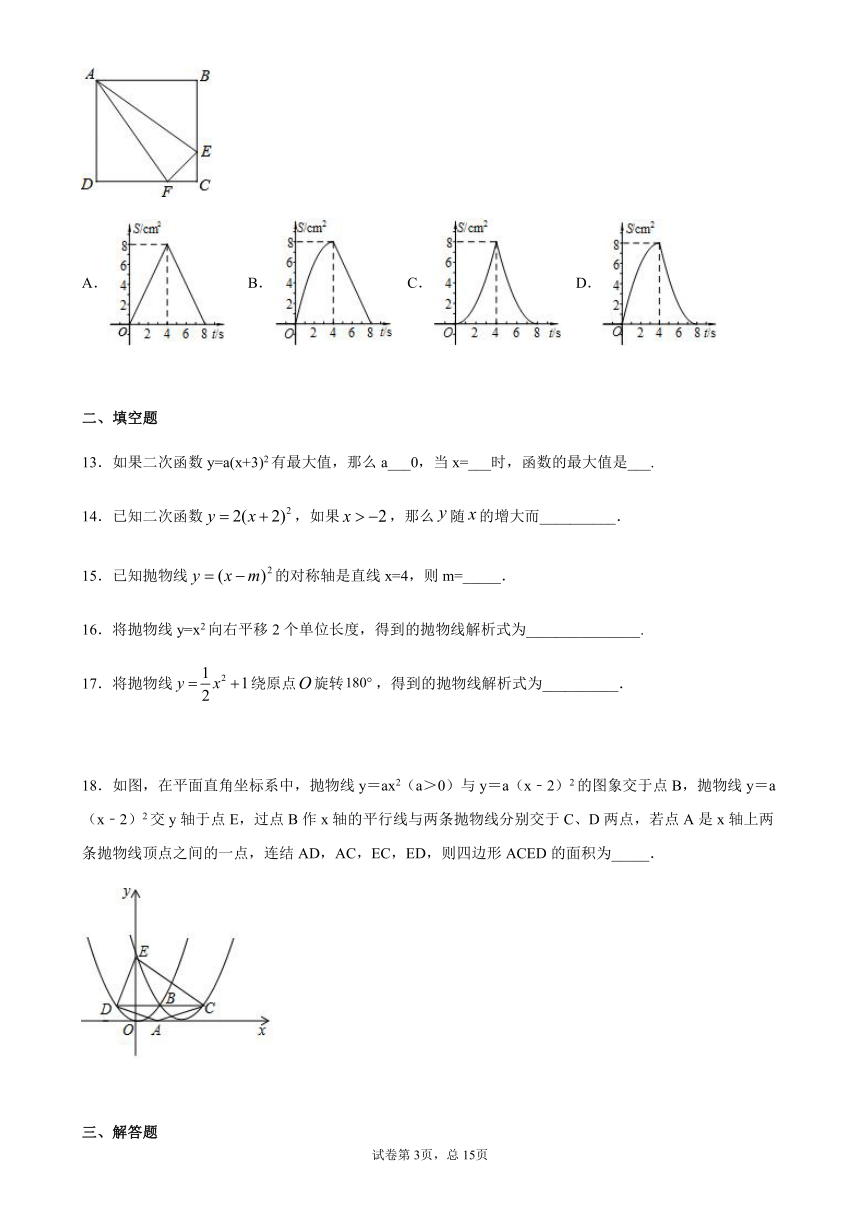
12.如图,正方形ABCD中,AB=4cm,点E、F同时从C点出发,以1cm/s的速度分别沿CB﹣BA、CD﹣DA运动,到点A时停止运动.设运动时间为t(s),△AEF的面积为S(cm2),则S(cm2)与t(s)的函数关系可用图象表示为( )
A.
B.
C.
D.
二、填空题
13.如果二次函数y=a(x+3)2有最大值,那么a___0,当x=___时,函数的最大值是___.
14.已知二次函数,如果,那么随的增大而__________.
15.已知抛物线的对称轴是直线x=4,则m=_____.
16.将抛物线y=x2向右平移2个单位长度,得到的抛物线解析式为_______________.
17.将抛物线绕原点旋转,得到的抛物线解析式为__________.
18.如图,在平面直角坐标系中,抛物线y=ax2(a>0)与y=a(x﹣2)2的图象交于点B,抛物线y=a(x﹣2)2交y轴于点E,过点B作x轴的平行线与两条抛物线分别交于C、D两点,若点A是x轴上两条抛物线顶点之间的一点,连结AD,AC,EC,ED,则四边形ACED的面积为_____.
三、解答题
19.请在同一坐标系中画出二次函数①;②的图象.说出两条抛物线的位置关系,指出②的开口方向、对称轴和顶点.
20.对于二次函数.
(1)它的图象与二次函数的图象有什么关系?它是轴对称图形吗?它的开口方向,对称轴和顶点坐标分别是什么?
(2)当取哪些值时,的值随的增大而增大?当取哪些值时,的值随的增大而减小?
21.如图,抛物线y=2(x-2)2与平行于x轴的直线交于点A,B,抛物线顶点为C,△ABC为等边三角形,求S△ABC
22.如图,抛物线y=ax2经过△ABC的三个顶点,点A坐标为(﹣1,2),点B是点A关于y轴的对称点,点C在x轴的正半轴上.
(1)求该抛物线的函数关系表达式;
(2)点F为线段AC上一动点,过F作FE⊥x轴,FG⊥y轴,垂足分别为E、G,当四边形OEFG为正方形时,求出F点的坐标.
23.如图,二次函数:=+)的图象与一次函数:=的图象交于A
(0,1),B两点,C(1,0)为二次函数图象的顶点.
(1)求二次函数:=+)的解析式.
(2)定义函数当自变量任取一值时,对应的函数值分别为或,若,函数的函数值等于、中的较小值;若,函数的函数值等于或.当直线->0)与函数的图象只有两个交点时,求的值.
24.如图,已知二次函数图象的顶点坐标为C(1,0),直线y=x+m与该二次函数的图象交于A、B两点,其中A点的坐标为(3,4),B点在y轴上.
(1)求m的值及这个二次函数的关系式;
(2)P为线段AB上的一个动点(点P与A、B不重合),过P作x轴的垂线与这个二次函数的图象交于点E,设线段PE的长为h,点P的横坐标为x.
①求h与x之间的函数关系式,并写出自变量x的取值范围;
②线段PE的长h是否存在最大值?若存在,求出此时P点的坐标;若不存在,请说明理由?
25.如图,顶点M在y轴上的抛物线与直线相交于A、B两点,且点A在x轴上,点B的横坐标为2,连结AM、BM.
(1)直接写出A点B点坐标及抛物线的函数关系式;
(2)判断△ABM的形状,并说明理由;
(3)把抛物线与直线的交点称为抛物线的不动点,若将(1)中抛物线平移,使其顶点为(m,2m),当m满足什么条件时,平移后的抛物线总有不动点.
参考答案
一、选择题
1
2
3
4
5
6
7
8
9
10
11
12
C
B
B
D
D
D
D
C
B
D
B
D
二、填空题
13
14
15
16
17
18
<,x=-3,0
增大
4
y=(x-2)2
8a
三、解答题
19.
解:列表:
-2
-1
0
1
2
3
4
2
0.5
0
0.5
2
2
0.5
0
0.5
2
描点,连线,如图
由图像可知,①向左平移两个单位得到②
∴②的开口方向向上,对称轴是,顶点坐标为(2,0)
20.
(1)将的图象向左平移个单位可以得到的图象
∵
∴抛物线开口向下
它是轴对称图形,对称轴为,顶点坐标是
∵,抛物线开口向下
∴当时,的值随的增大而增大;当时,的值随的增大而减小
21.
解:过B作BP⊥x轴交于点P,连接AC,BC,由抛物线y=得C(2,0)
∴对称轴为直线x=2
设B(m,n)
∴CP=m-2
∵AB∥x轴
∴AB=2m-4
∵△ABC是等边三角形
∴BC=AB=2m-4,∠BCP=∠ABC=60°
∴PB=PC=(m-2)
∵PB=n=
∴(m-2)=
解得m=,m=2(不合题意,舍去)
∴AB=,BP=
∴S△ABC=
22.
解:(1)∵
抛物线y=ax2经过△ABC的三个顶点,点A坐标为(﹣1,2)
∴
2=a,∴
a
∴
抛物线的函数关系表达式为y
(2)①当点F在第一象限时,如图1
令y=0得,0,解得:
∴点C的坐标为(3,0)
设直线AC的解析式为y=mx+n
则有,解得
∴直线AC的解析式为y
设正方形OEFG的边长为p,则F(p,p)
∵点F(p,p)在直线y上
∴p,解得p=1
∴点F的坐标为(1,1)
②当点F在第二象限时
同理可得:点F的坐标为(﹣3,3)
此时点F不在线段AC上,故舍去
综上所述:点F的坐标为(1,1)
23.
解:(1)设抛物线解析式为y1=a(x-1)2
由拋物线过点A(0,1),代入y1=a(x-1)2,求得a=1
所以
(2)∵
点A(0,1)在=上
∴
d=1
∴
=
将y=x2-2x+1与y=x+1联立解得:x=0,y=1或x=3,y=4,即B(3,4)
直线与函数f的图象只有两个交点共有三种情况:
①直线与直线AB:平行,此时k=1
②直线过点B(3,4),此时k
=
③直线与二次函数的图象只有一个交点
此时有,得:
=
由△
=
0,可得(舍去)
综上,k=1或k
=或
24.
解:(1)∵
点A(3,4)在直线y=x+m上
∴
4=3+m
∴
m=1
设所求二次函数的关系式为y=a(x﹣1)2
∵
点A(3,4)在二次函数y=a(x﹣1)2的图象上
∴
4=a(3﹣1)2
∴
a=1
∴
所求二次函数的关系式为y=(x﹣1)2
即y=x2﹣2x+1
(2)①设P、E两点的纵坐标分别为yP和yE
∴
PE=h=yP﹣yE=(x+1)﹣(x2﹣2x+1)=﹣x2+3x
即h=﹣x2+3x(0<x<3)
②存在.∵
h=﹣(x﹣)2+
又∵
a=﹣1<0
∴
x=时,h的值最大
当x=时,y=x+1=+1=
出此时点P的坐标(,)
25.
(1)∵点A是直线与轴的交点
∴A点为(-1,0)
∵点B在直线上,且横坐标为2
∴B点为(2,3)
∵过点A、B的抛物线的顶点M在轴上,故设其解析式为:
∴,解得:
∴抛物线的解析式为
(2)△ABM是直角三角形,且∠BAM=90°.理由如下:
作BC⊥轴于点C
∵A(-1,0)、B(2,3)
∴AC=BC=3
∴∠BAC=45°
点M是抛物线的顶点
∴M点为(0,-1)
∴OA=OM=1
∵∠AOM=90°
∴∠MAC=45°
∴∠BAM=∠BAC+∠MAC=90°
∴△ABM是直角三角形
(3)将抛物线的顶点平移至点(,),则其解析式为
∵抛物线的不动点是抛物线与直线的交点
∴
化简得:
∴△==
当时,方程总有实数根,即平移后的抛物线总有不动点,解得:,
∴
试卷第1页,总3页
试卷第1页,总3页
二次函数y=a(x-h)2的图象与性质(培优卷)
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.已知抛物线的开口向下,则的取值范围是(
)
A.
B.
C.
D.
2.抛物线y=2(x-1)2的对称轴是(
)
A.1
B.直线x=1
C.直线x=2
D.直线x=-1
3.对于二次函数的图象,下列说法正确的是(
)
A.开口向上
B.对称轴是x=-3
C.当x>-4
时,y随x的增大而减小
D.顶点坐标为(-2,-3)
4.在抛物线上的一个点是(?
)
A.(2,3)
B.(-2,3)
C.(1,-2)
D.(0,-2)
5.已知二次函数,当时,随着的增大而增大,当时,随的增大而减小,当时,的值为(
)
A.2
B.
C.4
D.
6.抛物线y=﹣2(x﹣1)2的图象上有三个点A(﹣1,y1),B(1,y2),C(2,y3),则y1,y2,y3的大小关系是( )
A.>>
B.
>>
C.>>
D.
>>
7.顶点为,开口向下,开口的大小与函数的图象相同的抛物线所对应的函数是(
)
A.
B.
C.
D.
8.已知二次函数y=-(x-3)2,对于x1<x2<3,x1、x2的对应函数值为y1、y2,则(
)
A.y1=y2
B.y1>y2
C.y1<y2
D.无法确定
9.在正比例函数中,随的增大而减小,则二次函数的图象大致是(
)
A.
B.
C.
D.
10.二次函数的图象如图,则下列正确的是(
)
A.,
B.,
C.,
D.,
11.如图,抛物线y=(x﹣h)2与x轴只有一个交点M,且与平行于x轴的直线l交于A、B两点,若AB=3,则点M到直线l的距离是( )
A.
B.
C.
D.
12.如图,正方形ABCD中,AB=4cm,点E、F同时从C点出发,以1cm/s的速度分别沿CB﹣BA、CD﹣DA运动,到点A时停止运动.设运动时间为t(s),△AEF的面积为S(cm2),则S(cm2)与t(s)的函数关系可用图象表示为( )
A.
B.
C.
D.
二、填空题
13.如果二次函数y=a(x+3)2有最大值,那么a___0,当x=___时,函数的最大值是___.
14.已知二次函数,如果,那么随的增大而__________.
15.已知抛物线的对称轴是直线x=4,则m=_____.
16.将抛物线y=x2向右平移2个单位长度,得到的抛物线解析式为_______________.
17.将抛物线绕原点旋转,得到的抛物线解析式为__________.
18.如图,在平面直角坐标系中,抛物线y=ax2(a>0)与y=a(x﹣2)2的图象交于点B,抛物线y=a(x﹣2)2交y轴于点E,过点B作x轴的平行线与两条抛物线分别交于C、D两点,若点A是x轴上两条抛物线顶点之间的一点,连结AD,AC,EC,ED,则四边形ACED的面积为_____.
三、解答题
19.请在同一坐标系中画出二次函数①;②的图象.说出两条抛物线的位置关系,指出②的开口方向、对称轴和顶点.
20.对于二次函数.
(1)它的图象与二次函数的图象有什么关系?它是轴对称图形吗?它的开口方向,对称轴和顶点坐标分别是什么?
(2)当取哪些值时,的值随的增大而增大?当取哪些值时,的值随的增大而减小?
21.如图,抛物线y=2(x-2)2与平行于x轴的直线交于点A,B,抛物线顶点为C,△ABC为等边三角形,求S△ABC
22.如图,抛物线y=ax2经过△ABC的三个顶点,点A坐标为(﹣1,2),点B是点A关于y轴的对称点,点C在x轴的正半轴上.
(1)求该抛物线的函数关系表达式;
(2)点F为线段AC上一动点,过F作FE⊥x轴,FG⊥y轴,垂足分别为E、G,当四边形OEFG为正方形时,求出F点的坐标.
23.如图,二次函数:=+)的图象与一次函数:=的图象交于A
(0,1),B两点,C(1,0)为二次函数图象的顶点.
(1)求二次函数:=+)的解析式.
(2)定义函数当自变量任取一值时,对应的函数值分别为或,若,函数的函数值等于、中的较小值;若,函数的函数值等于或.当直线->0)与函数的图象只有两个交点时,求的值.
24.如图,已知二次函数图象的顶点坐标为C(1,0),直线y=x+m与该二次函数的图象交于A、B两点,其中A点的坐标为(3,4),B点在y轴上.
(1)求m的值及这个二次函数的关系式;
(2)P为线段AB上的一个动点(点P与A、B不重合),过P作x轴的垂线与这个二次函数的图象交于点E,设线段PE的长为h,点P的横坐标为x.
①求h与x之间的函数关系式,并写出自变量x的取值范围;
②线段PE的长h是否存在最大值?若存在,求出此时P点的坐标;若不存在,请说明理由?
25.如图,顶点M在y轴上的抛物线与直线相交于A、B两点,且点A在x轴上,点B的横坐标为2,连结AM、BM.
(1)直接写出A点B点坐标及抛物线的函数关系式;
(2)判断△ABM的形状,并说明理由;
(3)把抛物线与直线的交点称为抛物线的不动点,若将(1)中抛物线平移,使其顶点为(m,2m),当m满足什么条件时,平移后的抛物线总有不动点.
参考答案
一、选择题
1
2
3
4
5
6
7
8
9
10
11
12
C
B
B
D
D
D
D
C
B
D
B
D
二、填空题
13
14
15
16
17
18
<,x=-3,0
增大
4
y=(x-2)2
8a
三、解答题
19.
解:列表:
-2
-1
0
1
2
3
4
2
0.5
0
0.5
2
2
0.5
0
0.5
2
描点,连线,如图
由图像可知,①向左平移两个单位得到②
∴②的开口方向向上,对称轴是,顶点坐标为(2,0)
20.
(1)将的图象向左平移个单位可以得到的图象
∵
∴抛物线开口向下
它是轴对称图形,对称轴为,顶点坐标是
∵,抛物线开口向下
∴当时,的值随的增大而增大;当时,的值随的增大而减小
21.
解:过B作BP⊥x轴交于点P,连接AC,BC,由抛物线y=得C(2,0)
∴对称轴为直线x=2
设B(m,n)
∴CP=m-2
∵AB∥x轴
∴AB=2m-4
∵△ABC是等边三角形
∴BC=AB=2m-4,∠BCP=∠ABC=60°
∴PB=PC=(m-2)
∵PB=n=
∴(m-2)=
解得m=,m=2(不合题意,舍去)
∴AB=,BP=
∴S△ABC=
22.
解:(1)∵
抛物线y=ax2经过△ABC的三个顶点,点A坐标为(﹣1,2)
∴
2=a,∴
a
∴
抛物线的函数关系表达式为y
(2)①当点F在第一象限时,如图1
令y=0得,0,解得:
∴点C的坐标为(3,0)
设直线AC的解析式为y=mx+n
则有,解得
∴直线AC的解析式为y
设正方形OEFG的边长为p,则F(p,p)
∵点F(p,p)在直线y上
∴p,解得p=1
∴点F的坐标为(1,1)
②当点F在第二象限时
同理可得:点F的坐标为(﹣3,3)
此时点F不在线段AC上,故舍去
综上所述:点F的坐标为(1,1)
23.
解:(1)设抛物线解析式为y1=a(x-1)2
由拋物线过点A(0,1),代入y1=a(x-1)2,求得a=1
所以
(2)∵
点A(0,1)在=上
∴
d=1
∴
=
将y=x2-2x+1与y=x+1联立解得:x=0,y=1或x=3,y=4,即B(3,4)
直线与函数f的图象只有两个交点共有三种情况:
①直线与直线AB:平行,此时k=1
②直线过点B(3,4),此时k
=
③直线与二次函数的图象只有一个交点
此时有,得:
=
由△
=
0,可得(舍去)
综上,k=1或k
=或
24.
解:(1)∵
点A(3,4)在直线y=x+m上
∴
4=3+m
∴
m=1
设所求二次函数的关系式为y=a(x﹣1)2
∵
点A(3,4)在二次函数y=a(x﹣1)2的图象上
∴
4=a(3﹣1)2
∴
a=1
∴
所求二次函数的关系式为y=(x﹣1)2
即y=x2﹣2x+1
(2)①设P、E两点的纵坐标分别为yP和yE
∴
PE=h=yP﹣yE=(x+1)﹣(x2﹣2x+1)=﹣x2+3x
即h=﹣x2+3x(0<x<3)
②存在.∵
h=﹣(x﹣)2+
又∵
a=﹣1<0
∴
x=时,h的值最大
当x=时,y=x+1=+1=
出此时点P的坐标(,)
25.
(1)∵点A是直线与轴的交点
∴A点为(-1,0)
∵点B在直线上,且横坐标为2
∴B点为(2,3)
∵过点A、B的抛物线的顶点M在轴上,故设其解析式为:
∴,解得:
∴抛物线的解析式为
(2)△ABM是直角三角形,且∠BAM=90°.理由如下:
作BC⊥轴于点C
∵A(-1,0)、B(2,3)
∴AC=BC=3
∴∠BAC=45°
点M是抛物线的顶点
∴M点为(0,-1)
∴OA=OM=1
∵∠AOM=90°
∴∠MAC=45°
∴∠BAM=∠BAC+∠MAC=90°
∴△ABM是直角三角形
(3)将抛物线的顶点平移至点(,),则其解析式为
∵抛物线的不动点是抛物线与直线的交点
∴
化简得:
∴△==
当时,方程总有实数根,即平移后的抛物线总有不动点,解得:,
∴
试卷第1页,总3页
试卷第1页,总3页
