2020-2021学年九年级数学浙教版下册 2.2 切线长定理 教案
文档属性
| 名称 | 2020-2021学年九年级数学浙教版下册 2.2 切线长定理 教案 |

|
|
| 格式 | zip | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-17 00:00:00 | ||
图片预览


文档简介
直角三角形与圆相切问题
再探究
一:教材、学情分析
杭州市近五年中考,对线圆相切问题考察不多,也不难。而今年考纲增加一条“切线长定理”,考试要求是C。二模之后,我们公办初中,保送生已走,也就是说二轮复习主要面向的群体是临界生。
2.复习目标
1.进一步深入理解切线的判定和性质.
2.培养学生在复杂图形中识别基本图形、构造基本图形的能力.
3.培养学生定性和定量两方面分析基本图形的意识和能力.
3.培养学生画图——识图——用图的意识和能力.
4.让学生经历问题解决的过程,培养学生剖析几何直观的数学素养和能力,获得解决几何问题的基本经验和方法.
三.课前准备
课前学生独立完成以下这道题:
如图,PA与⊙O相切于点A,过点A作AB⊥OP,垂足为C,交⊙O于点B.连接PB,AO,并延长AO交⊙O于点D,与PB的延长线交于点E.若ED=2,EB=
.
(1)求直径AD的长.
(2)求的值.
(3)连结CD和BD,请判断四边形PCDB的形状,并说明理由.
3.教学过程
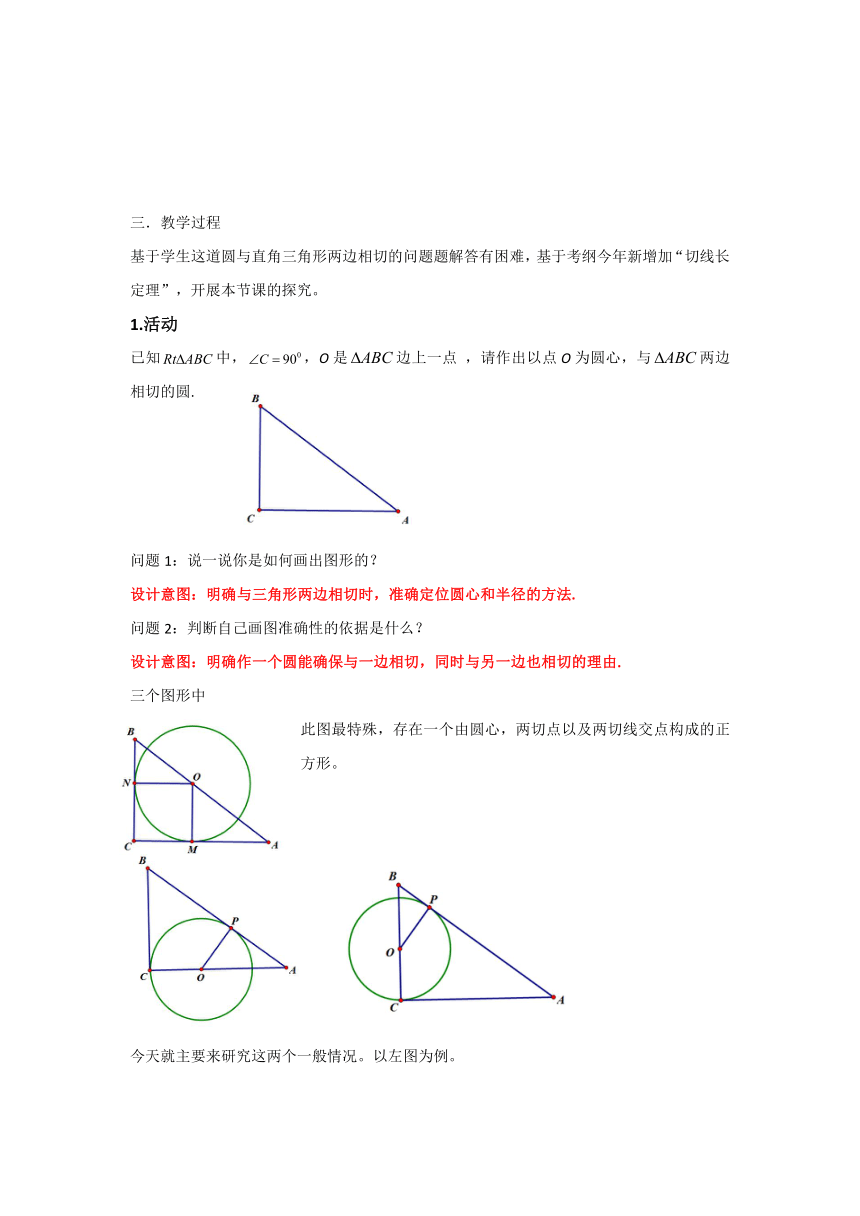
基于学生这道圆与直角三角形两边相切的问题题解答有困难,基于考纲今年新增加“切线长定理”,开展本节课的探究。
1.活动
已知中,,O是边上一点
,请作出以点O为圆心,与两边相切的圆.
问题1:说一说你是如何画出图形的?
设计意图:明确与三角形两边相切时,准确定位圆心和半径的方法.
问题2:判断自己画图准确性的依据是什么?
设计意图:明确作一个圆能确保与一边相切,同时与另一边也相切的理由.
三个图形中
此图最特殊,存在一个由圆心,两切点以及两切线交点构成的正方形。
今天就主要来研究这两个一般情况。以左图为例。
2.
探究一
已知中,
,BC=6,AC=8,⊙O与AC相交于点D,与BC、AB分别相切于点C和点P.求出⊙O的半径.
设计意图:经历用多种方法求线段长,获得几何图形中求线段长的本质是通过寻找等量关系建立方程,渗透方程思想.初步感受从复杂图形中分解出基本图形的必要性.
3.
探究二
在探究一的基础上,连结CP、DP.求出CP、DP的长.
设计意图:进一步巩固和体验三种求线段长的方法;在用多种方法求CP、DP的长度的过程中,提炼出基本型,感受从复杂图形中分解出基本图形的必要性。
再连结ED,四边形BEDP是平行四边形吗?
追问1:要使得四边形PCDB始终为平行四边形,三边需要满足什么条件?
追问2:四边形PCDB可能为菱形吗?为什么?
设计意图:经历从特殊到一般,再从一般到特殊的数学研究路径。
4.解决前测的问题
如图,PA与⊙O相切于点A,过点A作AB⊥OP,垂足为C,交⊙O于点B.连接PB,AO,并延长AO交⊙O于点D,与PB的延长线交于点E.若ED=2,EB=
.
(1)求直径AD的长.
(2)求的值.
(3)连结CD和BD,请判断四边形PCDB的形状,并说明理由.
经过剖析,(1)(2)(3)难度都不大了,只需点拨一下求某个角的三角函数值的方法。布置学生课后自己订正。
小结
问题:今天这节课,你的收获是什么?
设计意图:引导和培养学生定性和定量两方面分析基本图形的意识.从复杂图形中分解出基本图形的必要性。
回家作业
1.如图,AB是⊙O的直径,C是⊙O上的点,过点C作⊙O的切线交AB的延长线于点D,若∠A=32°,则∠D=____度.
2.如图,P是⊙O外一点,PO的延长线交⊙O于点A、B,点C在圆上,若PA=1,PC=3,则圆半径长为______.AC=______.
3.如图,AB是⊙O的直径,点C在⊙O上,连接BC,AC,作OD//BC与过点A的切线交于点D,连接DC并延长交AB的延长线于点E.
(1)求证:DE是⊙O的切线.
(2)若,求的值.
4.定义:圆心在三角形的一边上,与另一边相切,且经过三角形一个顶点(非切点)的圆,称为这个三角形圆心所在边上的“伴随圆”.
(1)如图1,△ABC中,∠C=90°,AB=5,BC=3,则AC边上的伴随圆的半径为___.
(2)如图2,已知等腰△ABC,AB=AC=5,BC=6,画草图并直接写出它的所有伴随圆的半径.
(3)如图3,△ABC中,∠ACB=90°,点P在边AB上,AP=2BP,D为AC中点,且∠CPD=90°.
①求证:△CPD的外接圆是△ABC某一条边上的伴随圆;
②求cos∠PDC的值.
再探究
一:教材、学情分析
杭州市近五年中考,对线圆相切问题考察不多,也不难。而今年考纲增加一条“切线长定理”,考试要求是C。二模之后,我们公办初中,保送生已走,也就是说二轮复习主要面向的群体是临界生。
2.复习目标
1.进一步深入理解切线的判定和性质.
2.培养学生在复杂图形中识别基本图形、构造基本图形的能力.
3.培养学生定性和定量两方面分析基本图形的意识和能力.
3.培养学生画图——识图——用图的意识和能力.
4.让学生经历问题解决的过程,培养学生剖析几何直观的数学素养和能力,获得解决几何问题的基本经验和方法.
三.课前准备
课前学生独立完成以下这道题:
如图,PA与⊙O相切于点A,过点A作AB⊥OP,垂足为C,交⊙O于点B.连接PB,AO,并延长AO交⊙O于点D,与PB的延长线交于点E.若ED=2,EB=
.
(1)求直径AD的长.
(2)求的值.
(3)连结CD和BD,请判断四边形PCDB的形状,并说明理由.
3.教学过程
基于学生这道圆与直角三角形两边相切的问题题解答有困难,基于考纲今年新增加“切线长定理”,开展本节课的探究。
1.活动
已知中,,O是边上一点
,请作出以点O为圆心,与两边相切的圆.
问题1:说一说你是如何画出图形的?
设计意图:明确与三角形两边相切时,准确定位圆心和半径的方法.
问题2:判断自己画图准确性的依据是什么?
设计意图:明确作一个圆能确保与一边相切,同时与另一边也相切的理由.
三个图形中
此图最特殊,存在一个由圆心,两切点以及两切线交点构成的正方形。
今天就主要来研究这两个一般情况。以左图为例。
2.
探究一
已知中,
,BC=6,AC=8,⊙O与AC相交于点D,与BC、AB分别相切于点C和点P.求出⊙O的半径.
设计意图:经历用多种方法求线段长,获得几何图形中求线段长的本质是通过寻找等量关系建立方程,渗透方程思想.初步感受从复杂图形中分解出基本图形的必要性.
3.
探究二
在探究一的基础上,连结CP、DP.求出CP、DP的长.
设计意图:进一步巩固和体验三种求线段长的方法;在用多种方法求CP、DP的长度的过程中,提炼出基本型,感受从复杂图形中分解出基本图形的必要性。
再连结ED,四边形BEDP是平行四边形吗?
追问1:要使得四边形PCDB始终为平行四边形,三边需要满足什么条件?
追问2:四边形PCDB可能为菱形吗?为什么?
设计意图:经历从特殊到一般,再从一般到特殊的数学研究路径。
4.解决前测的问题
如图,PA与⊙O相切于点A,过点A作AB⊥OP,垂足为C,交⊙O于点B.连接PB,AO,并延长AO交⊙O于点D,与PB的延长线交于点E.若ED=2,EB=
.
(1)求直径AD的长.
(2)求的值.
(3)连结CD和BD,请判断四边形PCDB的形状,并说明理由.
经过剖析,(1)(2)(3)难度都不大了,只需点拨一下求某个角的三角函数值的方法。布置学生课后自己订正。
小结
问题:今天这节课,你的收获是什么?
设计意图:引导和培养学生定性和定量两方面分析基本图形的意识.从复杂图形中分解出基本图形的必要性。
回家作业
1.如图,AB是⊙O的直径,C是⊙O上的点,过点C作⊙O的切线交AB的延长线于点D,若∠A=32°,则∠D=____度.
2.如图,P是⊙O外一点,PO的延长线交⊙O于点A、B,点C在圆上,若PA=1,PC=3,则圆半径长为______.AC=______.
3.如图,AB是⊙O的直径,点C在⊙O上,连接BC,AC,作OD//BC与过点A的切线交于点D,连接DC并延长交AB的延长线于点E.
(1)求证:DE是⊙O的切线.
(2)若,求的值.
4.定义:圆心在三角形的一边上,与另一边相切,且经过三角形一个顶点(非切点)的圆,称为这个三角形圆心所在边上的“伴随圆”.
(1)如图1,△ABC中,∠C=90°,AB=5,BC=3,则AC边上的伴随圆的半径为___.
(2)如图2,已知等腰△ABC,AB=AC=5,BC=6,画草图并直接写出它的所有伴随圆的半径.
(3)如图3,△ABC中,∠ACB=90°,点P在边AB上,AP=2BP,D为AC中点,且∠CPD=90°.
①求证:△CPD的外接圆是△ABC某一条边上的伴随圆;
②求cos∠PDC的值.
