浙教版初中数学七年级上册 2.1 有理数的加法(第1课时)教案(表格式)
文档属性
| 名称 | 浙教版初中数学七年级上册 2.1 有理数的加法(第1课时)教案(表格式) |
|
|
| 格式 | zip | ||
| 文件大小 | 118.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-18 00:00:00 | ||
图片预览


文档简介
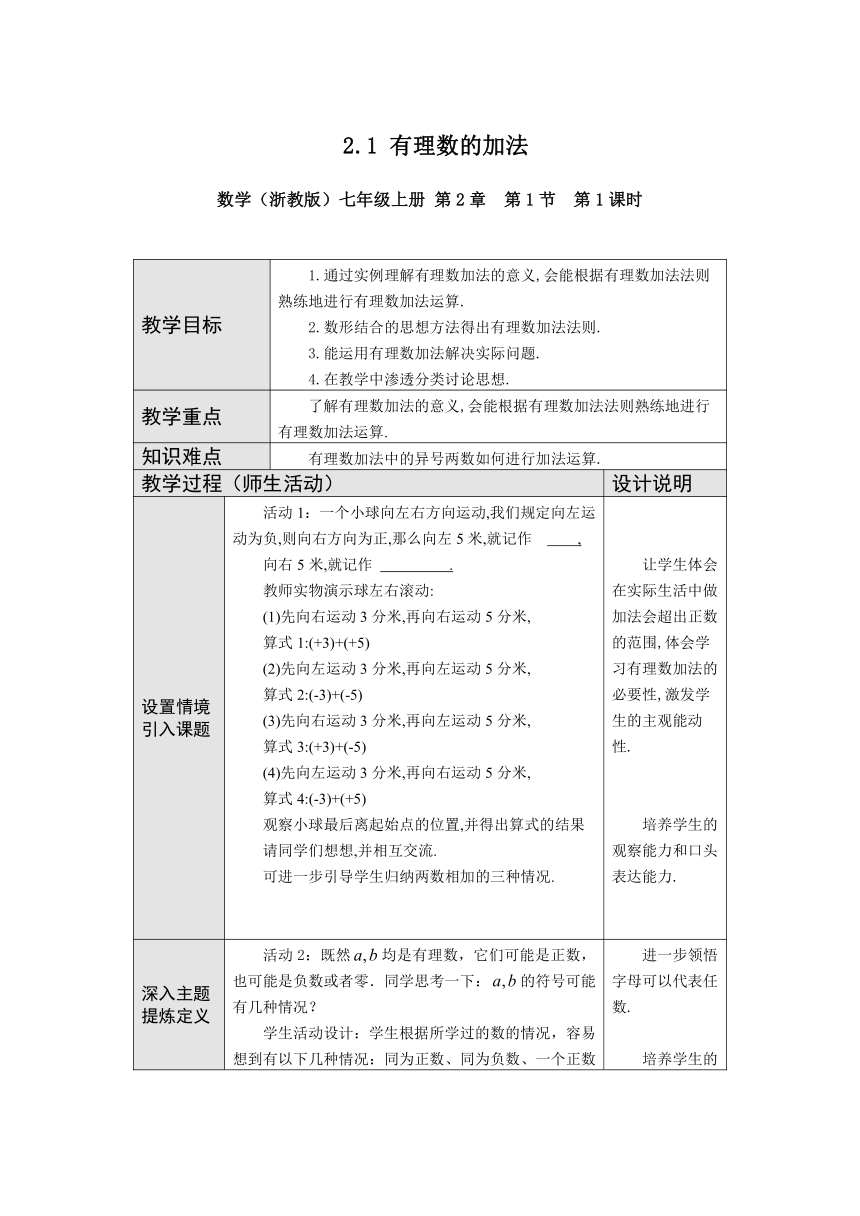
2.1
有理数的加法
数学(浙教版)七年级上册
第2章
第1节
第1课时
教学目标
1.通过实例理解有理数加法的意义,会能根据有理数加法法则熟练地进行有理数加法运算.2.数形结合的思想方法得出有理数加法法则.3.能运用有理数加法解决实际问题.4.在教学中渗透分类讨论思想.
教学重点
了解有理数加法的意义,会能根据有理数加法法则熟练地进行有理数加法运算.
知识难点
有理数加法中的异号两数如何进行加法运算.
教学过程(师生活动)
设计说明
设置情境引入课题
活动1:一个小球向左右方向运动,我们规定向左运动为负,则向右方向为正,那么向左5米,就记作
,向右5米,就记作
.教师实物演示球左右滚动:(1)先向右运动3分米,再向右运动5分米,算式1:(+3)+(+5)
(2)先向左运动3分米,再向左运动5分米,算式2:(-3)+(-5)(3)先向右运动3分米,再向左运动5分米,算式3:(+3)+(-5)(4)先向左运动3分米,再向右运动5分米,算式4:(-3)+(+5)观察小球最后离起始点的位置,并得出算式的结果请同学们想想,并相互交流.可进一步引导学生归纳两数相加的三种情况.
让学生体会在实际生活中做加法会超出正数的范围,体会学习有理数加法的必要性,激发学生的主观能动性.培养学生的观察能力和口头表达能力.
深入主题提炼定义
活动2:既然均是有理数,它们可能是正数,也可能是负数或者零.同学思考一下:的符号可能有几种情况?学生活动设计:学生根据所学过的数的情况,容易想到有以下几种情况:同为正数、同为负数、一个正数一个负数、加数中有一个是0;情况1.若同为正数:不妨设,用数轴表示如图:(有同学可能会说,这么简单不用数轴也能算出来.这时要告诉它,这里用数轴的目的并不是要结果,而是要体会过程,以便在其他的情况下为用数轴解决问题)显然一共走了35米,写出算式就是:(+20)+(+15)=+35
情况2.若同为负数:不妨设,这时应怎样用数轴表示?(学生画数轴)这时问题的实际意义是:我向西走了20米后,再向西走了15米,我实际向东走了-35米.即:
情况3.若一正一负:不妨设.请同学们用数轴表示出来,并解说这时问题的实际意义.(如图)(实际意义就是我向东走了20米以后,接着我又向西走了15米.我实际是向东走了5米)即:情况4.若呢?这时问题的实际意义是什么?怎样用数轴来表示?(同学操作)结果:
情况5.若时,这时问题的实际意义是什么?结果:
情况6.若时,这时问题的实际意义又是什么?结果:
情况7.若时,这时问题的实际意义是什么?结果:
情况8.若时,这时问题的实际意义是什么?结果:综合以上几种情况,得到8个式子,我们将这8个式子分成同号、异号、有零的三种情况统计如下:(1)同号的情况:;
.(2)异号的情况:;
;
;
.(3)有零的情况:;
有理数加法法则1、同号两数相加,取相同的符号,并把绝对值相加;2、异号两数相加时:
(1)若绝对值不相等,取绝对值较大加数的符号,并用较大的绝对值减去较小的绝对值;
(2)若绝对值相等,和为0.
也就是相反数的和为0;3、一个数与0的和仍得这个数.
进一步领悟字母可以代表任数.
培养学生的数形结合的思想及渗透分类讨论思想及化归思想.体会从特殊到一般的历程.注意学生合作学习方式,让学生在与他人合作中获益,学会交流,学会倾听.
题例精解解决问题
例1
(1);(2);
(3);(4);
(5);(6);
(7);.教师板演,请学生说出法则.请同学比较,有理数加法和小学学的加法有什么不同.例2
足球循环赛中,红队4比1
胜黄队,黄队1比0胜蓝队,蓝队1比0胜红队,计算各队的净胜球数.
利用所学知识求相反数,体验成功的喜悦。拓宽学生的视眼,体会数学与生活是密切联系.
课堂练习
练一练:书本第18页练习
巩固有理数加法的计算及法则
课堂小结
通过这节课的学习,你有什么收获?
本课作业
必做题:教科书第24,26页习题1.3第1,12,13题选做题:1.计算(1)
;(2);
(3);
(4);
(5).2.一只乌龟沿南北方向的河岸来回爬行,假定向北爬行的路程记为正数,向南爬行的路程记为负数,它爬行的过程记录如下(单位m):-8,7,-3,9,-6,-4,10.(1)乌龟最后距离出发点多远,在出发点的南边还是北边;
(2)求乌龟在整个过程中一共爬行了多远的距离
作业可设必做题和选
做题,体现要求的层次性,以满足不同学生的需要
o
B
A
20
15
35
1
有理数的加法
数学(浙教版)七年级上册
第2章
第1节
第1课时
教学目标
1.通过实例理解有理数加法的意义,会能根据有理数加法法则熟练地进行有理数加法运算.2.数形结合的思想方法得出有理数加法法则.3.能运用有理数加法解决实际问题.4.在教学中渗透分类讨论思想.
教学重点
了解有理数加法的意义,会能根据有理数加法法则熟练地进行有理数加法运算.
知识难点
有理数加法中的异号两数如何进行加法运算.
教学过程(师生活动)
设计说明
设置情境引入课题
活动1:一个小球向左右方向运动,我们规定向左运动为负,则向右方向为正,那么向左5米,就记作
,向右5米,就记作
.教师实物演示球左右滚动:(1)先向右运动3分米,再向右运动5分米,算式1:(+3)+(+5)
(2)先向左运动3分米,再向左运动5分米,算式2:(-3)+(-5)(3)先向右运动3分米,再向左运动5分米,算式3:(+3)+(-5)(4)先向左运动3分米,再向右运动5分米,算式4:(-3)+(+5)观察小球最后离起始点的位置,并得出算式的结果请同学们想想,并相互交流.可进一步引导学生归纳两数相加的三种情况.
让学生体会在实际生活中做加法会超出正数的范围,体会学习有理数加法的必要性,激发学生的主观能动性.培养学生的观察能力和口头表达能力.
深入主题提炼定义
活动2:既然均是有理数,它们可能是正数,也可能是负数或者零.同学思考一下:的符号可能有几种情况?学生活动设计:学生根据所学过的数的情况,容易想到有以下几种情况:同为正数、同为负数、一个正数一个负数、加数中有一个是0;情况1.若同为正数:不妨设,用数轴表示如图:(有同学可能会说,这么简单不用数轴也能算出来.这时要告诉它,这里用数轴的目的并不是要结果,而是要体会过程,以便在其他的情况下为用数轴解决问题)显然一共走了35米,写出算式就是:(+20)+(+15)=+35
情况2.若同为负数:不妨设,这时应怎样用数轴表示?(学生画数轴)这时问题的实际意义是:我向西走了20米后,再向西走了15米,我实际向东走了-35米.即:
情况3.若一正一负:不妨设.请同学们用数轴表示出来,并解说这时问题的实际意义.(如图)(实际意义就是我向东走了20米以后,接着我又向西走了15米.我实际是向东走了5米)即:情况4.若呢?这时问题的实际意义是什么?怎样用数轴来表示?(同学操作)结果:
情况5.若时,这时问题的实际意义是什么?结果:
情况6.若时,这时问题的实际意义又是什么?结果:
情况7.若时,这时问题的实际意义是什么?结果:
情况8.若时,这时问题的实际意义是什么?结果:综合以上几种情况,得到8个式子,我们将这8个式子分成同号、异号、有零的三种情况统计如下:(1)同号的情况:;
.(2)异号的情况:;
;
;
.(3)有零的情况:;
有理数加法法则1、同号两数相加,取相同的符号,并把绝对值相加;2、异号两数相加时:
(1)若绝对值不相等,取绝对值较大加数的符号,并用较大的绝对值减去较小的绝对值;
(2)若绝对值相等,和为0.
也就是相反数的和为0;3、一个数与0的和仍得这个数.
进一步领悟字母可以代表任数.
培养学生的数形结合的思想及渗透分类讨论思想及化归思想.体会从特殊到一般的历程.注意学生合作学习方式,让学生在与他人合作中获益,学会交流,学会倾听.
题例精解解决问题
例1
(1);(2);
(3);(4);
(5);(6);
(7);.教师板演,请学生说出法则.请同学比较,有理数加法和小学学的加法有什么不同.例2
足球循环赛中,红队4比1
胜黄队,黄队1比0胜蓝队,蓝队1比0胜红队,计算各队的净胜球数.
利用所学知识求相反数,体验成功的喜悦。拓宽学生的视眼,体会数学与生活是密切联系.
课堂练习
练一练:书本第18页练习
巩固有理数加法的计算及法则
课堂小结
通过这节课的学习,你有什么收获?
本课作业
必做题:教科书第24,26页习题1.3第1,12,13题选做题:1.计算(1)
;(2);
(3);
(4);
(5).2.一只乌龟沿南北方向的河岸来回爬行,假定向北爬行的路程记为正数,向南爬行的路程记为负数,它爬行的过程记录如下(单位m):-8,7,-3,9,-6,-4,10.(1)乌龟最后距离出发点多远,在出发点的南边还是北边;
(2)求乌龟在整个过程中一共爬行了多远的距离
作业可设必做题和选
做题,体现要求的层次性,以满足不同学生的需要
o
B
A
20
15
35
1
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
