4.1比例线段

(共30张PPT)
回 忆
小学学过了比例的有关知识，什么是比例？怎样表示比例？说出比例中各部分的名称、比例的基本性质是什么？
表示两个比相等的式子叫比例，如果 a 与 b 的比值和 c 与 d 的
比值相等，那么 或写成 a ：b = c ：d.
外项
外项
内项
内项
a ：b = c ：d.
外项
内项
比例的基本性质:
在比例中，两个外项的积等于两个内项的积.
用式子表示是：
如果 (b、d 都不为零），那么ad = bc.
比例线段
画两个矩形ABCD和A′ B ′ C ′D ′，使它们的长分别为4.5cm 和 1.5cm，宽分别为2.4cm和0.8cm，并计算线段AB和BC的比，线段A′ B ′ 和B ′ C ′的比.
A
B
C
D
A′
B′
C′
D′
结论：
在四条线段 a、b、c、d 中，如果 a 和 b 的比等于 c 和 d 的比，那么这四条线段a、b、c、d 叫做成比例的线段，简称比例线段.
外项
外项
内项
内项
a ：b = c ：d.
外项
内项
a、b、c 的第四比例项
如果作为比例内项的是两条相等的线段即 或
a ：b = b ：c， 那么线段 b 叫做线段 a 和 c 的比例中项.
两条线段的比是它们的长度的比，
也就是两个数的比.
关于成比例的数具有下面的性质.
比例式是等式，
因而具有等式的各个性质，
此外还有一些特殊性质：
(1)比例的基本性质
如果 a：b =c：d ，那么ad =bc.
因为 a：b=c：d，
即
a c
b d
= ，
比例的内项乘积等于外项乘积.
两边同乘以 bd，得 ad=bc；
上述性质反过来也对，就是
如果 ad =bc，那么 a：b =c：d .
(1)比例的基本性质
a：b=c：d ad=bc.
特殊地说：
a：b=b：c b =ac.
2
综合地说：
如果
PA PC
PB PD
= ，
那么 PA·
PD=
如果
CD DF
EB AD
= ，
那么 AD·
CD=
如果
AC BD
EF EA
= ，
那么 EF·
BD=
如果
HE HF
NF NK
= ，
那么 HF·
NF=
PB·PC；
EB·DF；
AC·EA；
HE·NK；
如果
AD PB
PB BC
= ，
那么 AD·
BC=
如果
DE DF
DF DC
= ，
那么 DE·
DC=
如果
SB EF
EF SC
= ，
那么 EF
2=
如果
MA NF
NF MB
= ，
那么 NF
2=
PB2；
DF2；
SB·SC；
MA·MB.
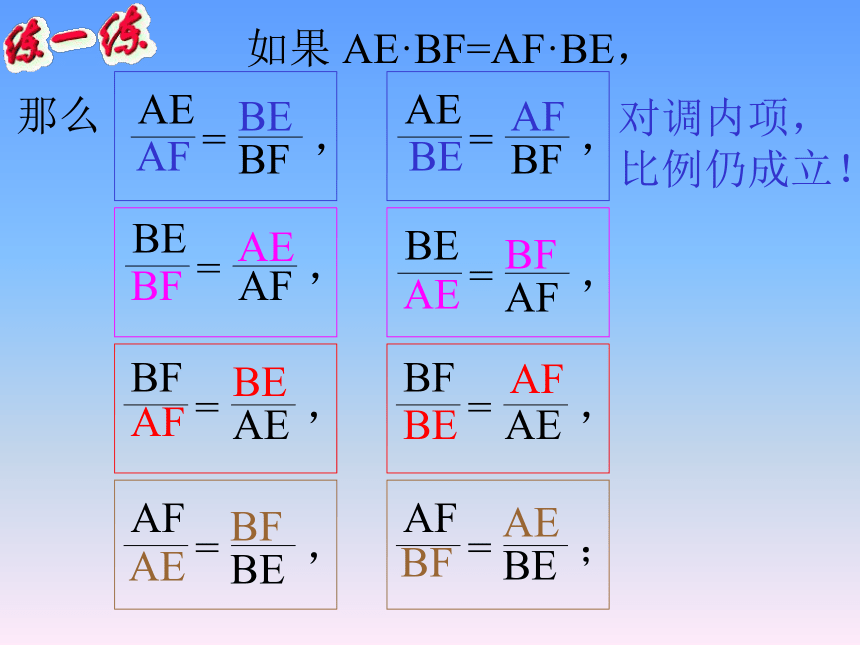
如果 AE·BF=AF·BE，
AE
= ，
那么
BE
= ，
BF
= ，
AF
= ；
BE
= ，
BF
= ，
AF
= ，
AE
= ，
AF
BE
BF
BE
AF
BF
AF
AE
BF
AE
BF
AF
AF
BE
AE
AF
BE
AE
AE
BF
BE
BF
AE
BE
对调内项，
比例仍成立！
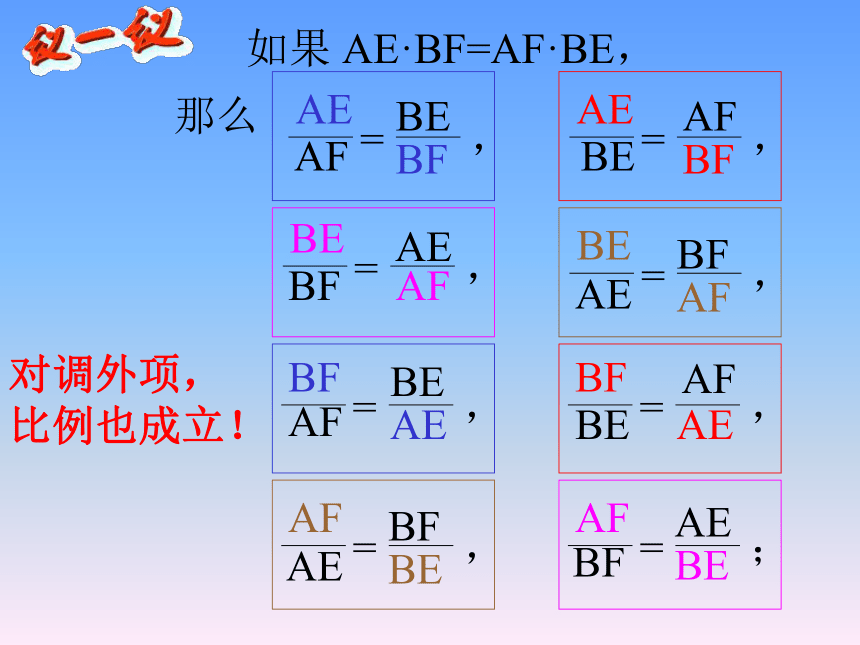
如果 AE·BF=AF·BE，
AE
= ，
那么
BE
= ，
BF
= ，
AF
= ；
BE
= ，
BF
= ，
AF
= ，
AE
= ，
AF
BE
BF
BE
AF
BF
AF
AE
BF
AE
BF
AF
AF
BE
AE
AF
BE
AE
AE
BF
BE
BF
AE
BE
对调外项，
比例也成立！
说明：
(1)一个等积式可以改写成八个比例式
(比值各不相同)；
(2)对调比例式的内项或外项，
比例式仍然成立
(比值变了).
a c
b d
=
a b
c d
=
d c
b a
= .
如果 AE·BF=AF·BE，
AE
= ，
那么
BE
= ，
BF
= ，
AF
= ；
BE
= ，
BF
= ，
AF
= ，
AE
= ，
AF
BE
BF
BE
AF
BF
AF
AE
BF
AE
BF
AF
AF
BE
AE
AF
BE
AE
AE
BF
BE
BF
AE
BE
说明：
同时对调比例式两边的比的前后项，
比例式仍然成立
(比值变了).
a c
b d
=
b d
a c
= .
如果 PA·PB=PC·PD，
PA
= ，
那么
PB
= ，
PC
= ，
PD
= ；
PB
= ，
PC
= ，
PD
= ，
PA
= ，
PC
PD
PB
PD
PC
PB
PA
PD
PC
PD
PC
PA
PA
PB
PD
PA
PB
PD
PA
PB
PC
PB
PA
PC
如果 AE·CF=AB·AD，
AE
= ，
那么
CF
= ，
AB
= ，
AD
= ；
CF
= ，
AB
= ，
AD
= ，
AE
= ，
AB
AD
CF
AD
AB
CF
AE
AD
AB
AD
AB
AE
AE
CF
AD
AE
CF
AD
AE
CF
AB
CF
AE
AB
如果 AC2=AB·AD，
AC
= ，
那么
AB
= ；
AB
AD
AC
AC
AC
AD
如果 PT2=PQ·PR，
PT
= ，
那么
PQ
= .
PQ
PR
PT
PT
PT
PR
(2)合比性质
如果
a c
b d
= ，
那么
a±b c±d
b d
= .
证明
练习3—1：
如图，已知
AC
BC
= ，
那么
AB DE
BC EF
= ，
DF
EF
理由：
AB DE
BC EF
=
AC DF
BC EF
= .
AB+BC DE+EF
BC EF
=
A
B
C
D
E
F
练习3—2：
如图，已知
AC
AB
= ，
那么
AB DE
BC EF
= ，
DF
DE
理由：
AB DE
BC EF
=
AB+BC DE+EF
AB DE
=
BC EF
AB DE
=
AC DF
AB DE
= .
A
B
C
D
E
F
(3)等比性质
如果
那么
a c
b d
=
m
n
= …=
(b+d+…+n≠0),
a+c+…+m
b+d+…+n
= .
a
b
a c
b d
=
m
n
= …=
证明：
设
=k,
则
a=bk,
c=dk,
…
m=nk,
∴ =
a+c+…+m
b+d+…+n
bk+dk+…nk
b+d+…n
=
(b+d+…n)k
b+d+…n
=k
= .
a
b
a c
b d
=
m
n
= …=
a+c+…+m
b+d+…+n
= .
a
b
？
比例的性质
1、比例的基本性质：
如果 a ：b = c ：d ，那么 ad = bc.
如果 ad = bc，那么 a ：b = c ：d
2、合比性质：
如果 ，那么
3、等比性质：
如果 ，
那么 .
例1 从ad = bc ，根据什么性质,可以得到 d ：b = c ： a
从ad = bc 还可以得到那些比例
解:
∵ ad = bc ,两边同除以 ac 得:
即 d ： c = b ： a ;
∵ ad = bc ,两边同除以 db 得:
即 a ： b = c ： d ;
∵ ad = bc ,两边同除以 dc 得:
即 a ： c = b ： d ;
∵ ad = bc ,两边同除以 ab 得:
即 d ： b = c ： a ;
(比例的基本性质)
左右两边对调
左右两边对调
左右两边对调
左右两边对调
x+y 5 x
3y 4 y
例2、已知 = ，求 .
解：
∵ = ，
x+y 5
3y 4
x+y 15
y 4
∴ = ，
x+y–y 15–4
y 4
∴ = ，
x 11
y 4
∴ = .
例3、已知 a：b：c=2：5：6，
求 的值.
2a+5b–c
3a–2b+c
解：
设 = = = k,
a b c
2 5 6
则 a=2k,
b=5k,
c=6k,
2a+5b–c
3a–2b+c
∴ =
4k+25k–6k
6k–10k+6k
=
23
2
.
练习
⑴若m 是2、3、8 的第四比例项，则 m= ；
⑵若x 是3和27的比例中项，则 x = ；
⑶若 a ：b ：c = 2 ： 3 ：7 ,又 a + b + c = 36，
则 a = ，b = ，c = .
12
9
6
9
21
⑷已知 ，则 .
比例线段的概念
a ：b = c ：d.
外项
内项
a、b、c 的第四比例项
a ：b = b ：c
比例中项
a、b、b的第四比例项
在四条线段 a、b、c、d 中，如果 a 和 b 的比等于 c 和 d 的比，那么这四条线段a、b、c、d 叫做成比例的线段，简称比例线段.
小 结
如果 a ：b = c ：d ，那么 ad = bc.
如果 ad = bc，那么 a ：b = c ：d
基本性质
如果 ，那么
合比性质
如果 ，
那么 .
等比性质
比例的性质