浙教版初中数学七年级上册 6.5 角与角的度量 教案
文档属性
| 名称 | 浙教版初中数学七年级上册 6.5 角与角的度量 教案 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-20 11:44:52 | ||
图片预览


文档简介
6.5
角与角的度量
【教学目标】
知识目标:1、使学生进一步认识角的有关概念,掌握角的表示方法。
2、理解平角、周角的意义。
能力目标:使学生正确掌握“角、分、秒”的互化,会进行角度的和、差计算.
【教学重点、难点】
重点:角的概念和角的表示法、角度的和、差计算。
难点:角的多种表示法,从运动的观点给出的角的概念。
【教学准备】量角器、圆规、三角板。
【教学过程】
1、
引入新课
在小学里,我们已经初步认识了“角”,请一位同学在黑板上中画出你所认为的“角”(四个),其他同学在草稿纸上画。
“角”的图形你在生活中的物体中有见过吗?你能在下图中找到角吗?
(1)
指出图中的角(试着画出来)
(2)
图中所指的角共同特征是
(3)
根据角的特征试用一句话概括角的定义:角是由
二、新课教学
1.角的概念:
(1)角的第一定义:角是由两条有公共端点的射线所组成的图形。
这个公共端点叫做角的顶点,这两条射线叫做角的边。(对照图形讲解)
用圆规摆成一个角的形状,请同学们说出什么是角的顶点?什么是角的边?
(2)关于角的第二定义(动态):
教师在PPT中展示角的动态形成过程,通过运动,展示出运动从初始状态到终止状态的过程。
然后归纳出角的概念:角也是由一条射线绕着它的端点旋转而成的图形。其中起始位置的射线叫做角的始边,终止位置叫做角的终边。
想一想:这种定义的含义与第一种定义的的含义有什么相同与不同的地方?
相同处:两种定义方法都揭示了角的两个基本特征:①有公共端点;②有两条射线组成。
不同处:用第二种方法,对角的指向更为明确,并且为今后的学习打下了伏笔。
(3)认识平角与周角
教师在PPT中演示,当角的终边继续旋转,旋转到与始边成同一直线。
教师提问:此时形成的角是什么角?
学生回答:平角。
继续提问:那么1平角等于?
继续回答:1平角=180°
教师在PPT中演示,当角的终边继续旋转,旋转到与始边重合。
教师提问:此时形成的角是什么角?
学生回答:周角。
继续提问:那么1周角等于?
继续回答:1周角=360°
2.角的表示:
(1)这节课刚开始的时候我们请同学在黑板画了四个角,那么怎样去描述这四个角呢?我么需要去表示角。
(2)角用符号“∠”表示,读做“角”,通常有以下几种表示方法:
①用三个大写字母来表示,其中表示顶点的字母一定要写在另两个字母的中间。
如下图中的角可以表示成∠AOB或∠BOA.中间的字母O表示顶点,其他两个字母A,B分别表示角的两边上的点.
②用顶点的字母表示(当以某一点为顶点的角多于一个时,不能用这种方法表示角)
如下左图中的角可以表示成∠O;
教师提问:那么如下右图中的角能不能用∠O表示?
学生回答:不可以
教师提问:为什么?
学生回答:因为这里有三个角,不知道∠O是哪一个角?
教师提问:那么我们在用一个顶点字母表示角的时候应该注意什么地方?
学生回答:只能有一个角
教师补充:当顶点只是这个角的顶点时,可以用一个顶点字母表示角;当以某一点为顶点的角多于一个时,不能用这种方法表示角,因此,这种方法虽然简单,但局限性大。
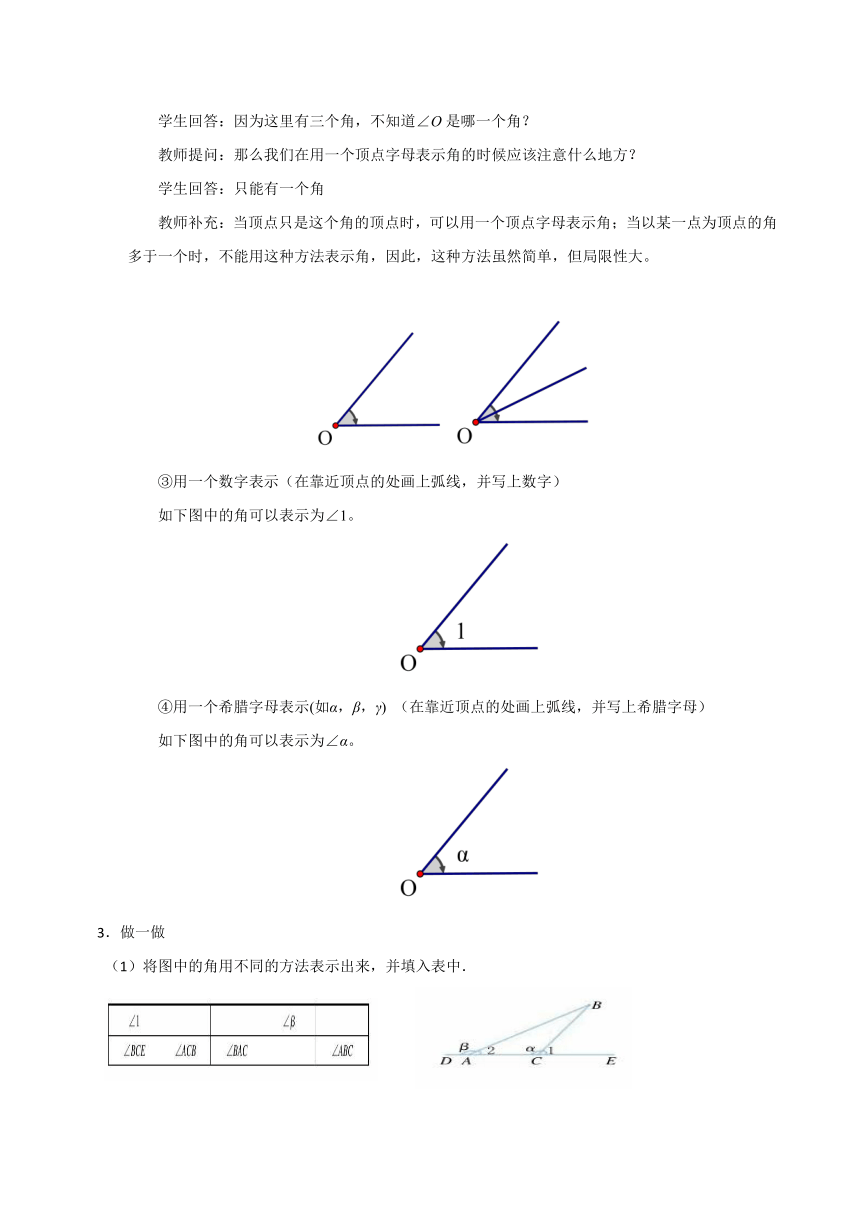
③用一个数字表示(在靠近顶点的处画上弧线,并写上数字)
如下图中的角可以表示为∠1。
④用一个希腊字母表示(如α,β,γ)
(在靠近顶点的处画上弧线,并写上希腊字母)
如下图中的角可以表示为∠α。
3.做一做
(1)将图中的角用不同的方法表示出来,并填入表中.
(2)将图中的角用不同的方法表示出来,并填入表中.
下列语句正确的是(
)
A.两条直线相交,组成的图形叫做角
B.两条有公共端点的线段组成的图形叫角
C.两条有公共点的射线组成的图形叫角
D.从同一点引出的两条射线组成的图形叫角
4.角的度量
(1)角的测量
教师提问:这节课刚开始的时候我们请同学在黑板画了四个角,那么我们刚才讲这四个角除了我们刚才讲的表示方法不同之外,还有什么地方不一样?
学生回答:大小也不一样。
继续提问:也就是说角有大小,那么角的大小可以用什么工具来测量?
学生回答:量角器。
继续提问:那么用量角器来测量角的时候应该注意什么地方?
(2)量角器的使用步骤
①对中:使量角器的圆心与角的顶点重合;
②对线:使量角器的零度数与角的一边重合;
③读数:看角的另一边落在量角器的哪条刻度数线(或靠近哪一条刻度线),从刻度线读出角的度数。
(3)角的度量单位
①那我们就赶紧动一动手,量一量刚开始在草稿纸上的画的那个角。
教师提问:你量出来的角度是多少?(请几位同学回答)
学生回答:35°、68°、41°
教师提问:在测量中,你遇到哪些问题?
学生回答:有时候读数的时候不是很确定,正好在两个刻度之间,不知道该读哪一个?
继续提问:也就是说我们在实际操作过程中发现“角”只用“度”作为单位精度是不够的!
②为此,除了“度”我们规定“分·”“秒”做为角更小的度量单位,其中度用“°”表示,分用“′”表示,秒用“〞”表示。
把1°的角等分成60等份,每一份是1′;而把1分的角再等分60份,每一份就是1秒,记作1〞。
角度制:1°=60′,1
′=〞
1′=60〞,1〞=
′
5.度、分、秒的互化及角的和差计算
练习(1)0.25°等于多少分?等于多少秒?
练习(2)2700〞等于多少分?等于多少度?
三、课堂练习、巩固新知
例1用度、分、秒表示48.32°
(说明:(1)度、分、秒的互化是60进制的,由不足1度化分,由不足1分化秒。
(2)在进行单位互化时,应明确是进行量的互化,而不是数的互化。在计算中,要逐级运算,步骤合理,计算正确。)
练习(3)用度、分、秒表示45.6°
(4)用度、分、秒表示78.43°
例2用度表示37°12′18〞
例3(1)30°19′
(2)180°-126°34′23〞
(说明:计算时按角、分、秒分别进行、再逐级进位和逐级退位,退、进位按六十进制换算。)
四、课堂小结
1.角是非常重要的一种几何基本图形.角有两种定义方法,但其实质是一致的,要抓住角的两个基本特征:有公共端点,有两条射线组成。
2.角有三种表示方法,各有优缺点,因此在实际应用中,要掌握两个原则:第一简明,第二正确。
3.角的测量。
4.角的度量单位:度、分、秒及换算。
五、布置作业:见作业本
六、板书设计
角与角的度量
【教学目标】
知识目标:1、使学生进一步认识角的有关概念,掌握角的表示方法。
2、理解平角、周角的意义。
能力目标:使学生正确掌握“角、分、秒”的互化,会进行角度的和、差计算.
【教学重点、难点】
重点:角的概念和角的表示法、角度的和、差计算。
难点:角的多种表示法,从运动的观点给出的角的概念。
【教学准备】量角器、圆规、三角板。
【教学过程】
1、
引入新课
在小学里,我们已经初步认识了“角”,请一位同学在黑板上中画出你所认为的“角”(四个),其他同学在草稿纸上画。
“角”的图形你在生活中的物体中有见过吗?你能在下图中找到角吗?
(1)
指出图中的角(试着画出来)
(2)
图中所指的角共同特征是
(3)
根据角的特征试用一句话概括角的定义:角是由
二、新课教学
1.角的概念:
(1)角的第一定义:角是由两条有公共端点的射线所组成的图形。
这个公共端点叫做角的顶点,这两条射线叫做角的边。(对照图形讲解)
用圆规摆成一个角的形状,请同学们说出什么是角的顶点?什么是角的边?
(2)关于角的第二定义(动态):
教师在PPT中展示角的动态形成过程,通过运动,展示出运动从初始状态到终止状态的过程。
然后归纳出角的概念:角也是由一条射线绕着它的端点旋转而成的图形。其中起始位置的射线叫做角的始边,终止位置叫做角的终边。
想一想:这种定义的含义与第一种定义的的含义有什么相同与不同的地方?
相同处:两种定义方法都揭示了角的两个基本特征:①有公共端点;②有两条射线组成。
不同处:用第二种方法,对角的指向更为明确,并且为今后的学习打下了伏笔。
(3)认识平角与周角
教师在PPT中演示,当角的终边继续旋转,旋转到与始边成同一直线。
教师提问:此时形成的角是什么角?
学生回答:平角。
继续提问:那么1平角等于?
继续回答:1平角=180°
教师在PPT中演示,当角的终边继续旋转,旋转到与始边重合。
教师提问:此时形成的角是什么角?
学生回答:周角。
继续提问:那么1周角等于?
继续回答:1周角=360°
2.角的表示:
(1)这节课刚开始的时候我们请同学在黑板画了四个角,那么怎样去描述这四个角呢?我么需要去表示角。
(2)角用符号“∠”表示,读做“角”,通常有以下几种表示方法:
①用三个大写字母来表示,其中表示顶点的字母一定要写在另两个字母的中间。
如下图中的角可以表示成∠AOB或∠BOA.中间的字母O表示顶点,其他两个字母A,B分别表示角的两边上的点.
②用顶点的字母表示(当以某一点为顶点的角多于一个时,不能用这种方法表示角)
如下左图中的角可以表示成∠O;
教师提问:那么如下右图中的角能不能用∠O表示?
学生回答:不可以
教师提问:为什么?
学生回答:因为这里有三个角,不知道∠O是哪一个角?
教师提问:那么我们在用一个顶点字母表示角的时候应该注意什么地方?
学生回答:只能有一个角
教师补充:当顶点只是这个角的顶点时,可以用一个顶点字母表示角;当以某一点为顶点的角多于一个时,不能用这种方法表示角,因此,这种方法虽然简单,但局限性大。
③用一个数字表示(在靠近顶点的处画上弧线,并写上数字)
如下图中的角可以表示为∠1。
④用一个希腊字母表示(如α,β,γ)
(在靠近顶点的处画上弧线,并写上希腊字母)
如下图中的角可以表示为∠α。
3.做一做
(1)将图中的角用不同的方法表示出来,并填入表中.
(2)将图中的角用不同的方法表示出来,并填入表中.
下列语句正确的是(
)
A.两条直线相交,组成的图形叫做角
B.两条有公共端点的线段组成的图形叫角
C.两条有公共点的射线组成的图形叫角
D.从同一点引出的两条射线组成的图形叫角
4.角的度量
(1)角的测量
教师提问:这节课刚开始的时候我们请同学在黑板画了四个角,那么我们刚才讲这四个角除了我们刚才讲的表示方法不同之外,还有什么地方不一样?
学生回答:大小也不一样。
继续提问:也就是说角有大小,那么角的大小可以用什么工具来测量?
学生回答:量角器。
继续提问:那么用量角器来测量角的时候应该注意什么地方?
(2)量角器的使用步骤
①对中:使量角器的圆心与角的顶点重合;
②对线:使量角器的零度数与角的一边重合;
③读数:看角的另一边落在量角器的哪条刻度数线(或靠近哪一条刻度线),从刻度线读出角的度数。
(3)角的度量单位
①那我们就赶紧动一动手,量一量刚开始在草稿纸上的画的那个角。
教师提问:你量出来的角度是多少?(请几位同学回答)
学生回答:35°、68°、41°
教师提问:在测量中,你遇到哪些问题?
学生回答:有时候读数的时候不是很确定,正好在两个刻度之间,不知道该读哪一个?
继续提问:也就是说我们在实际操作过程中发现“角”只用“度”作为单位精度是不够的!
②为此,除了“度”我们规定“分·”“秒”做为角更小的度量单位,其中度用“°”表示,分用“′”表示,秒用“〞”表示。
把1°的角等分成60等份,每一份是1′;而把1分的角再等分60份,每一份就是1秒,记作1〞。
角度制:1°=60′,1
′=〞
1′=60〞,1〞=
′
5.度、分、秒的互化及角的和差计算
练习(1)0.25°等于多少分?等于多少秒?
练习(2)2700〞等于多少分?等于多少度?
三、课堂练习、巩固新知
例1用度、分、秒表示48.32°
(说明:(1)度、分、秒的互化是60进制的,由不足1度化分,由不足1分化秒。
(2)在进行单位互化时,应明确是进行量的互化,而不是数的互化。在计算中,要逐级运算,步骤合理,计算正确。)
练习(3)用度、分、秒表示45.6°
(4)用度、分、秒表示78.43°
例2用度表示37°12′18〞
例3(1)30°19′
(2)180°-126°34′23〞
(说明:计算时按角、分、秒分别进行、再逐级进位和逐级退位,退、进位按六十进制换算。)
四、课堂小结
1.角是非常重要的一种几何基本图形.角有两种定义方法,但其实质是一致的,要抓住角的两个基本特征:有公共端点,有两条射线组成。
2.角有三种表示方法,各有优缺点,因此在实际应用中,要掌握两个原则:第一简明,第二正确。
3.角的测量。
4.角的度量单位:度、分、秒及换算。
五、布置作业:见作业本
六、板书设计
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
