2021年浙教版七年级数学上册暑假预习练习(Word版含解答):3.3 立方根
文档属性
| 名称 | 2021年浙教版七年级数学上册暑假预习练习(Word版含解答):3.3 立方根 |  | |
| 格式 | docx | ||
| 文件大小 | 70.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-28 09:35:44 | ||
图片预览




文档简介
2021年浙教版七年级数学上册暑假预习练习(Word版含解答):3.3 立方根
一、选择题
1.3-8 的相反数是(? )
A.?2??????????????????????B.?4????????????????C.?-2??????????????????????D.?-4
2.有下列说法:①负数没有立方根;②不带根号的数一定是有理数;③有理数和数轴上的点一对应;④ -7 是7的平方根,其中正确的( ???)
A.?0个????????????????????????B.?1个??????????????????C.?2个?????????????????????????????D.?3个
3.如果 3x=-3y ,则x,y的关系是(??? )
A.?x=y???????????????B.?x=±y????????????????C.?x=-y????????????D.?无法确定
4.以下计算正确的是(??? ).
A.?(-5)2=-5??????B.?38=±2???????????C.?±327=±3????????D.?(-2)2=-2
5.已知4m+15的算术平方根是3,2-6n的立方根是-2,则 6n-4m =(?? )
A.?2?????????????????????????B.?±2???????????????????????????C.?4???????????????????????D.?±4
6.在 0,-327,π,|-3| 这四个数中,最小的数是(? )
A.?0??????????????B.?π???????????????????????C.?|-3|????????????D.?-327
7.下列实数: 253,327,π3,3-4,(3)2,8,0.218,-52 ,其中无理数有(?? )
A.?5个??????????????????B.?4个??????????????????????C.?3个??????????????????????D.?2个
8.下列命题中,是真命题的是(?? )
A.?1 的平方根是 -1??????????????????B.?5 是 25 的一个平方根
C.?64 的立方根是 ±4????????????????D.?(-2)2 的平方根是 -2
9.一个正方体的水晶砖,体积为 80cm3 ,它的棱长大约在(??? )
A.?4cm-5cm 之间??????B.?6cm-7cm 之间??????C.?7cm-8cm 之间????D.?8cm-9cm 之间
10.已知a的算术平方根是12.3,b的立方根是-45.6,x的平方根是±1.23,y的立方根是456,则x和y分别是(?? )
A.?x=a1000,y=100b????????????????????B.?x=1000a,y=b1000
C.?x=a100,y=-1000b????????????????D.?x=a100,y=1000b
二、填空题
11.? 3的平方根是________,9的算术平方根是________,27的立方根是________.
12.计算: 4+3-8= ________.
13.比较大小:4________ 327 .(填“>”、“<”、“=”)
14.小明在作业本上做了4道题① 3-125 =﹣5;②± 16 =4;③ 381 =9;④ (-6)2 =﹣6,他做对的题有________.
15.已知 a、b 是有理数,若 a2=64,?b3=64 ,则 a+b 的所有值为________.
16.已知实数a+b的平方根是 ±4 ,实数 13a 的立方根是 -2 ,则 16a+b 的平方根为为________.
17.如果 |a+3|+b-2=0 ,那么 (2a-b) 的立方根是________.
18.我国数学家华罗庚在一次出国访问途中,看到飞机上邻座的乘客阅读的杂志上有一道智力题:求59319的立方根,华罗庚脱口说出答案,众人十分惊奇,忙问计算的奥妙.你知道他是怎样迅速准确地计算出结果的吗?
下面是小超的探究过程,请补充完整:
(1)求 359319 ;
①由103=1000,1003=1 000 000,可以确定 359319 是________位数;
②由59319的个位上的数是9,可以确定 359319 的个位上的数是________;
③如果划去59319后面的三位319得到数59,而33=27,43=64,可以确定 359319 的十位上的数是________;
由此求得 359319 =________.
(2)已知103823也是一个整数的立方,用类似的方法可以求得 3103823 =________.
三、解答题
19.计算:|-3|-(-1)+ 3-27 - 4
20.在数轴上表示下列各数,并用“<”连接起来。
-(-2) ?,? -|-3.5| ?,? 0 ,???14 ,?? -22 ,???3-27 。
21.李师傅打算把一个长、宽、高分别为50cm,8cm,20cm的长方体铁块锻造成一个立方体铁块,问锻造成的立方体铁块的棱长是多少cm?
22.将一个体积为 125cm3 的立方体体积增加V,而保持立方体的形状不变,则棱长应该增加多少?(用含有V的代数式表示);若 V=875cm3 ,则棱长应增加多少厘米?
23.已知 2a-1 的算术平方根是3, 10 的整数部分是 b , c 的立方根是 -2 ,求 3b-a-c 的平方根.
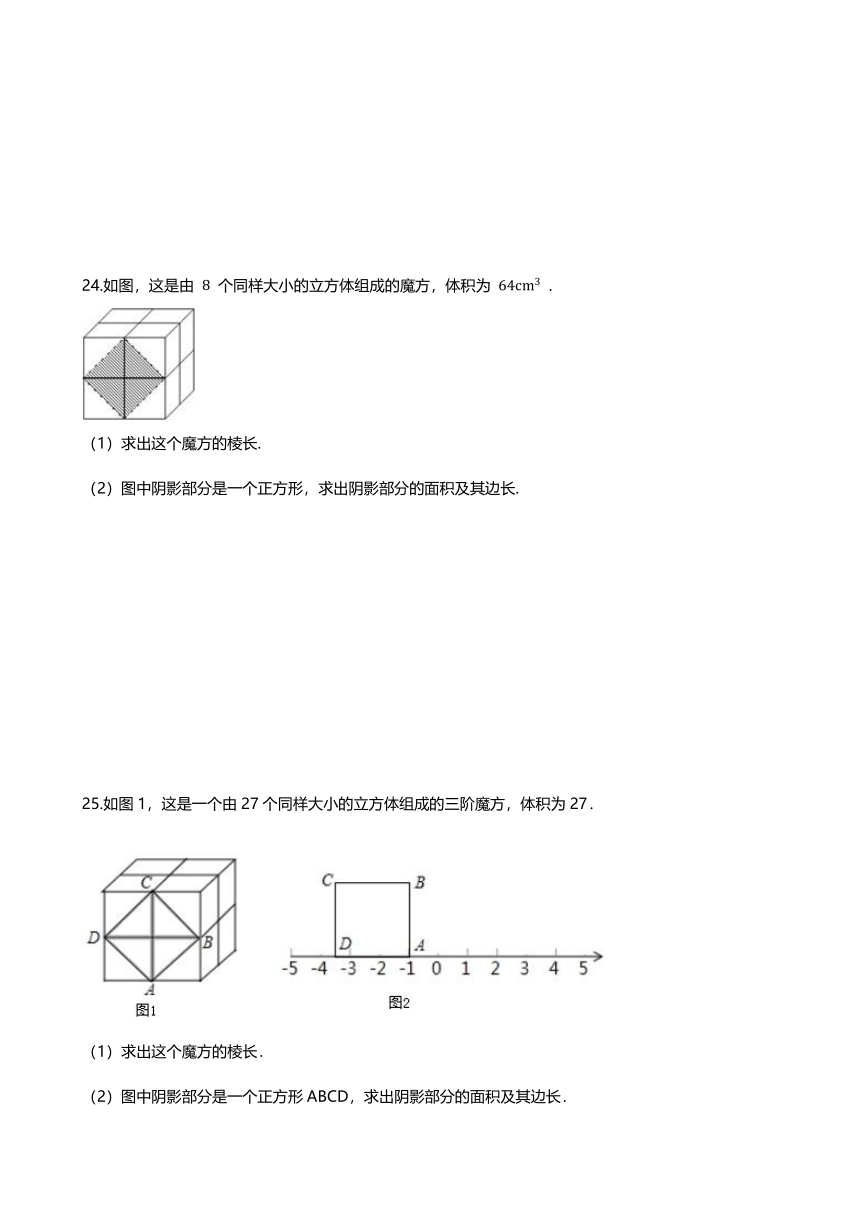
24.如图,这是由 8 个同样大小的立方体组成的魔方,体积为 64cm3 .
(1)求出这个魔方的棱长.
(2)图中阴影部分是一个正方形,求出阴影部分的面积及其边长.
25.如图1,这是一个由27个同样大小的立方体组成的三阶魔方,体积为27.
(1)求出这个魔方的棱长.
(2)图中阴影部分是一个正方形ABCD,求出阴影部分的面积及其边长.
(3)如图2,把图1中的正方形ABCD放到数轴上,使得点A与?1重合,那么点D在数轴上表示的数为.
答案
一、选择题
1.因为 3-8 =-2,
所以 3-8 的相反数是2
故答案为:A
2.①实数和数轴上的点一一对应,故①说法错误;
②不带根号的数不一定是有理数,如π , 故②说法错误;
③负数由立方根,故③说法错误;
④因为7的平方根为±7 , 所以7是7的一个平方根,故④说法正确。
故答案为:B
3.解:∵ 3x=-3y=3-y ,
∴ x=-y ,
故答案为:C.
4.解:A.原式=5,计算错误;
B.原式=2,计算错误;
C.原式=±3,计算正确;
D.原式=2,计算错误。
故答案为:C.
5.解:由题意可得:4m+15=9,2-6n=-8,解得: m=-32 , n=53
∴ 6n-4m=6×53-4×(-32)=16=4
故答案为:C
6.∵ -327=-3,|-3|=3,
∵-3<0<3<π
∴在 0,-327,π,|-3| 这四个数中,最小的数是 -327 .
故答案为:D
7.解: 253=8.3 ,小数点后的3是无限循环的,属于有理数;
327=3 , (3)2=3 属于有理数; 0.218 小数点后的218是无限循环的,属于有理数;
∴无理数有 π3 , 3-4 , 8=22 , -52 ,共计4个;
故答案为:B.
8.解:A、1的平方根是±1,原命题是假命题,不符合题意;
B、5是25的一个平方根,是真命题,符合题意;
C、64的立方根是4,原命题是假命题,不符合题意;
D、(-2)2的平方根是±2,原命题是假命题,不符合题意.
故答案为:B.
9.解:∵正方体的水晶砖,体积为 80cm3 ,
∴它的棱长是 380cm3 ,
∵ 364<380<3125 ,
∴ 4<380<5 ,
故答案为:A.
10.解:∵a的算术平方根是12.3,b的立方根是-45.6,x的平方根是±1.23,y的立方根是456,
∴a=12.32=100×1.232,b=-45.63,
x=1.232,y=1000×-45.63
∴x=a100,y=1000b.
故答案为:C.
二、填空题
11.解:3的平方根是± 3 ,9的算术平方根是3,27的立方根是3.
故答案为:± 3 ,3,3.
12.解: 4+3-8= 2-2= 0.
故答案为:0.
13.解:∵ 327=3 ,
∴ 4>3 ,即 4>327 ,
故答案为: > .
14.解:① 3-125 =﹣5,正确;
②± 16 =±4,故②错误;
③ 381=333 ≠9,故③错误;
④ (-6)2 =-6=6,故④错误.
∴他做对的题有1道.
故答案为:1道.
15.解:∵a2=64,b3=64,
∴a=±8,b=4,
∴当a=8,b=4时,
∴a+b=8+4=12,
当a=-8,b=4时,
∴a+b=-8+4=-4,
故答案为:12或-4.
16.解:∵实数a+b的平方根是 ±4 ,实数 13a 的立方根是 -2 ,
∴ a+b=16 , a= -24
∴ b= 40,
∴ 16a+b=16×(-24)+40=36
∴ ±16a+b=±36=±6
所以填 ±6 .
17.解: ∵|a+3|+b-2=0 ,
∴{a+3=0b-2=0, ?
∴{a=-3b=2, ?
∴2a-b=2×(-3)-2=-8, ?
∴2a-b 的立方根是-2
故答案为:-2
18. (1)两;9;3;39
(2)47
解:(1)①∵103=1000,1003=1 000 000,而1000<59319<100000,
∴10< 359319 <100,
因此结果为两位数;
②因为只有9的立方的个位数字才是9,因此结果的个位数字为9,
③33<59<43 , 因此可以确定 359319 的十位上的数是3,
最后得出 359319 =39,
故答案为:两,9,3、39;(2)∵103=1000,1003=1 000 000,而1000<103823<1000000,
∴10< 3103823 <100,
因此结果为两位数;
只有7的立方的个位数字是3,因此结果的个位数字是7;
如果划去103823后面的三位823得到数103,而43=64,53=125,可以确定 3103823 的十位数字为4,
于是可得 3103823 =47;
故答案为:47.
三、解答题
19. 解: 原式=3+1+(-3)-2=-1
20. 解:-(-2)=2,-|-3.5|=-3.5,14=12 , (-2)2=4,3-27=-3
--3.5<3-27<0<14<--2<-22.
21. 解:立方体的棱长=50×8×20=8000=20cm?.
答:立方体铁块的棱长为20cm.
22. 解:依题意得:棱长应该增加:
3125+V-3125=3125+V-5 (厘米),
当 V=875 时,
3125+V-5=3125+875-5=10-5=5 (厘米).
23. 解:∵ 2a-1 的算术平方根是3,
∴ 2a-1 =9
∴a=5
∵3< 10 <4,∴ 10 的整数部分是3
∴b=3
∵ c 的立方根是 -2
∴c=-8
∴ 3b-a-c =12
∴ 12=23
∴ 3b-a-c 的平方根是± 23 .
24.(1)解: 364=4 (cm)
(2)解:∵魔方的棱长为4cm,∴小立方体的棱长为2cm,∴阴影部分面积为: 12 ×2×2×4=8(cm2),边长为: 8 = 22 (cm).
25. (1)解:设魔方的棱长为 x ,
则 x3=27 ,解得: x=3
(2)解: ∵ 棱长为3,
∴ 每个小立方体的边长都是1,
∴ 正方形 ABCD 的边长为: 12+22=5 ,
∴S正方形ABCD=(5)2=5
(3)解: ∵ 正方形 ABCD 的边长为 5 ,点 A 与 -1 重合,
∴ 点 D 在数轴上表示的数为: -1-5 ,
故答案为: -1-5
一、选择题
1.3-8 的相反数是(? )
A.?2??????????????????????B.?4????????????????C.?-2??????????????????????D.?-4
2.有下列说法:①负数没有立方根;②不带根号的数一定是有理数;③有理数和数轴上的点一对应;④ -7 是7的平方根,其中正确的( ???)
A.?0个????????????????????????B.?1个??????????????????C.?2个?????????????????????????????D.?3个
3.如果 3x=-3y ,则x,y的关系是(??? )
A.?x=y???????????????B.?x=±y????????????????C.?x=-y????????????D.?无法确定
4.以下计算正确的是(??? ).
A.?(-5)2=-5??????B.?38=±2???????????C.?±327=±3????????D.?(-2)2=-2
5.已知4m+15的算术平方根是3,2-6n的立方根是-2,则 6n-4m =(?? )
A.?2?????????????????????????B.?±2???????????????????????????C.?4???????????????????????D.?±4
6.在 0,-327,π,|-3| 这四个数中,最小的数是(? )
A.?0??????????????B.?π???????????????????????C.?|-3|????????????D.?-327
7.下列实数: 253,327,π3,3-4,(3)2,8,0.218,-52 ,其中无理数有(?? )
A.?5个??????????????????B.?4个??????????????????????C.?3个??????????????????????D.?2个
8.下列命题中,是真命题的是(?? )
A.?1 的平方根是 -1??????????????????B.?5 是 25 的一个平方根
C.?64 的立方根是 ±4????????????????D.?(-2)2 的平方根是 -2
9.一个正方体的水晶砖,体积为 80cm3 ,它的棱长大约在(??? )
A.?4cm-5cm 之间??????B.?6cm-7cm 之间??????C.?7cm-8cm 之间????D.?8cm-9cm 之间
10.已知a的算术平方根是12.3,b的立方根是-45.6,x的平方根是±1.23,y的立方根是456,则x和y分别是(?? )
A.?x=a1000,y=100b????????????????????B.?x=1000a,y=b1000
C.?x=a100,y=-1000b????????????????D.?x=a100,y=1000b
二、填空题
11.? 3的平方根是________,9的算术平方根是________,27的立方根是________.
12.计算: 4+3-8= ________.
13.比较大小:4________ 327 .(填“>”、“<”、“=”)
14.小明在作业本上做了4道题① 3-125 =﹣5;②± 16 =4;③ 381 =9;④ (-6)2 =﹣6,他做对的题有________.
15.已知 a、b 是有理数,若 a2=64,?b3=64 ,则 a+b 的所有值为________.
16.已知实数a+b的平方根是 ±4 ,实数 13a 的立方根是 -2 ,则 16a+b 的平方根为为________.
17.如果 |a+3|+b-2=0 ,那么 (2a-b) 的立方根是________.
18.我国数学家华罗庚在一次出国访问途中,看到飞机上邻座的乘客阅读的杂志上有一道智力题:求59319的立方根,华罗庚脱口说出答案,众人十分惊奇,忙问计算的奥妙.你知道他是怎样迅速准确地计算出结果的吗?
下面是小超的探究过程,请补充完整:
(1)求 359319 ;
①由103=1000,1003=1 000 000,可以确定 359319 是________位数;
②由59319的个位上的数是9,可以确定 359319 的个位上的数是________;
③如果划去59319后面的三位319得到数59,而33=27,43=64,可以确定 359319 的十位上的数是________;
由此求得 359319 =________.
(2)已知103823也是一个整数的立方,用类似的方法可以求得 3103823 =________.
三、解答题
19.计算:|-3|-(-1)+ 3-27 - 4
20.在数轴上表示下列各数,并用“<”连接起来。
-(-2) ?,? -|-3.5| ?,? 0 ,???14 ,?? -22 ,???3-27 。
21.李师傅打算把一个长、宽、高分别为50cm,8cm,20cm的长方体铁块锻造成一个立方体铁块,问锻造成的立方体铁块的棱长是多少cm?
22.将一个体积为 125cm3 的立方体体积增加V,而保持立方体的形状不变,则棱长应该增加多少?(用含有V的代数式表示);若 V=875cm3 ,则棱长应增加多少厘米?
23.已知 2a-1 的算术平方根是3, 10 的整数部分是 b , c 的立方根是 -2 ,求 3b-a-c 的平方根.
24.如图,这是由 8 个同样大小的立方体组成的魔方,体积为 64cm3 .
(1)求出这个魔方的棱长.
(2)图中阴影部分是一个正方形,求出阴影部分的面积及其边长.
25.如图1,这是一个由27个同样大小的立方体组成的三阶魔方,体积为27.
(1)求出这个魔方的棱长.
(2)图中阴影部分是一个正方形ABCD,求出阴影部分的面积及其边长.
(3)如图2,把图1中的正方形ABCD放到数轴上,使得点A与?1重合,那么点D在数轴上表示的数为.
答案
一、选择题
1.因为 3-8 =-2,
所以 3-8 的相反数是2
故答案为:A
2.①实数和数轴上的点一一对应,故①说法错误;
②不带根号的数不一定是有理数,如π , 故②说法错误;
③负数由立方根,故③说法错误;
④因为7的平方根为±7 , 所以7是7的一个平方根,故④说法正确。
故答案为:B
3.解:∵ 3x=-3y=3-y ,
∴ x=-y ,
故答案为:C.
4.解:A.原式=5,计算错误;
B.原式=2,计算错误;
C.原式=±3,计算正确;
D.原式=2,计算错误。
故答案为:C.
5.解:由题意可得:4m+15=9,2-6n=-8,解得: m=-32 , n=53
∴ 6n-4m=6×53-4×(-32)=16=4
故答案为:C
6.∵ -327=-3,|-3|=3,
∵-3<0<3<π
∴在 0,-327,π,|-3| 这四个数中,最小的数是 -327 .
故答案为:D
7.解: 253=8.3 ,小数点后的3是无限循环的,属于有理数;
327=3 , (3)2=3 属于有理数; 0.218 小数点后的218是无限循环的,属于有理数;
∴无理数有 π3 , 3-4 , 8=22 , -52 ,共计4个;
故答案为:B.
8.解:A、1的平方根是±1,原命题是假命题,不符合题意;
B、5是25的一个平方根,是真命题,符合题意;
C、64的立方根是4,原命题是假命题,不符合题意;
D、(-2)2的平方根是±2,原命题是假命题,不符合题意.
故答案为:B.
9.解:∵正方体的水晶砖,体积为 80cm3 ,
∴它的棱长是 380cm3 ,
∵ 364<380<3125 ,
∴ 4<380<5 ,
故答案为:A.
10.解:∵a的算术平方根是12.3,b的立方根是-45.6,x的平方根是±1.23,y的立方根是456,
∴a=12.32=100×1.232,b=-45.63,
x=1.232,y=1000×-45.63
∴x=a100,y=1000b.
故答案为:C.
二、填空题
11.解:3的平方根是± 3 ,9的算术平方根是3,27的立方根是3.
故答案为:± 3 ,3,3.
12.解: 4+3-8= 2-2= 0.
故答案为:0.
13.解:∵ 327=3 ,
∴ 4>3 ,即 4>327 ,
故答案为: > .
14.解:① 3-125 =﹣5,正确;
②± 16 =±4,故②错误;
③ 381=333 ≠9,故③错误;
④ (-6)2 =-6=6,故④错误.
∴他做对的题有1道.
故答案为:1道.
15.解:∵a2=64,b3=64,
∴a=±8,b=4,
∴当a=8,b=4时,
∴a+b=8+4=12,
当a=-8,b=4时,
∴a+b=-8+4=-4,
故答案为:12或-4.
16.解:∵实数a+b的平方根是 ±4 ,实数 13a 的立方根是 -2 ,
∴ a+b=16 , a= -24
∴ b= 40,
∴ 16a+b=16×(-24)+40=36
∴ ±16a+b=±36=±6
所以填 ±6 .
17.解: ∵|a+3|+b-2=0 ,
∴{a+3=0b-2=0, ?
∴{a=-3b=2, ?
∴2a-b=2×(-3)-2=-8, ?
∴2a-b 的立方根是-2
故答案为:-2
18. (1)两;9;3;39
(2)47
解:(1)①∵103=1000,1003=1 000 000,而1000<59319<100000,
∴10< 359319 <100,
因此结果为两位数;
②因为只有9的立方的个位数字才是9,因此结果的个位数字为9,
③33<59<43 , 因此可以确定 359319 的十位上的数是3,
最后得出 359319 =39,
故答案为:两,9,3、39;(2)∵103=1000,1003=1 000 000,而1000<103823<1000000,
∴10< 3103823 <100,
因此结果为两位数;
只有7的立方的个位数字是3,因此结果的个位数字是7;
如果划去103823后面的三位823得到数103,而43=64,53=125,可以确定 3103823 的十位数字为4,
于是可得 3103823 =47;
故答案为:47.
三、解答题
19. 解: 原式=3+1+(-3)-2=-1
20. 解:-(-2)=2,-|-3.5|=-3.5,14=12 , (-2)2=4,3-27=-3
--3.5<3-27<0<14<--2<-22.
21. 解:立方体的棱长=50×8×20=8000=20cm?.
答:立方体铁块的棱长为20cm.
22. 解:依题意得:棱长应该增加:
3125+V-3125=3125+V-5 (厘米),
当 V=875 时,
3125+V-5=3125+875-5=10-5=5 (厘米).
23. 解:∵ 2a-1 的算术平方根是3,
∴ 2a-1 =9
∴a=5
∵3< 10 <4,∴ 10 的整数部分是3
∴b=3
∵ c 的立方根是 -2
∴c=-8
∴ 3b-a-c =12
∴ 12=23
∴ 3b-a-c 的平方根是± 23 .
24.(1)解: 364=4 (cm)
(2)解:∵魔方的棱长为4cm,∴小立方体的棱长为2cm,∴阴影部分面积为: 12 ×2×2×4=8(cm2),边长为: 8 = 22 (cm).
25. (1)解:设魔方的棱长为 x ,
则 x3=27 ,解得: x=3
(2)解: ∵ 棱长为3,
∴ 每个小立方体的边长都是1,
∴ 正方形 ABCD 的边长为: 12+22=5 ,
∴S正方形ABCD=(5)2=5
(3)解: ∵ 正方形 ABCD 的边长为 5 ,点 A 与 -1 重合,
∴ 点 D 在数轴上表示的数为: -1-5 ,
故答案为: -1-5
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
