5.5平行四边形的判定(2)

(共11张PPT)
判定一个四边形是平行四边形已学过哪些方法
定义：两组对边分别平行的四边形叫平行四边形。
定理1 一组对边平行并且相等的四边形
是平行四边形。
定理2 两组对边分别相等的四边形是
平行四边形。
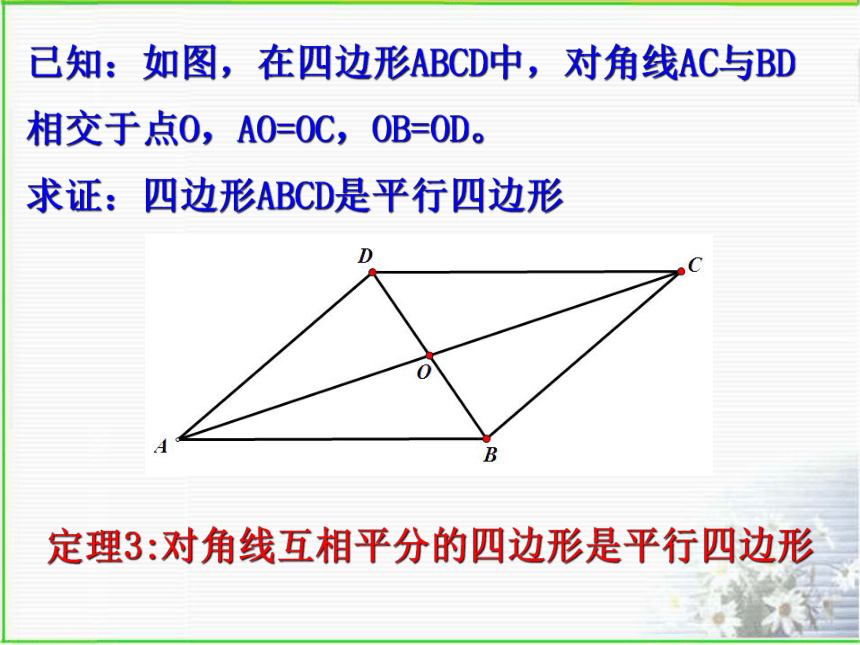
已知：如图，在四边形ABCD中，对角线AC与BD相交于点O，AO=OC，OB=OD。 求证：四边形ABCD是平行四边形
定理3:对角线互相平分的四边形是平行四边形
已知：
求证：
定理3:对角线互相平分的四边形是平行四边形
如图，在四边形ABCD中，对角线AC
与BD相交于点O，AO=OC，OB=OD。
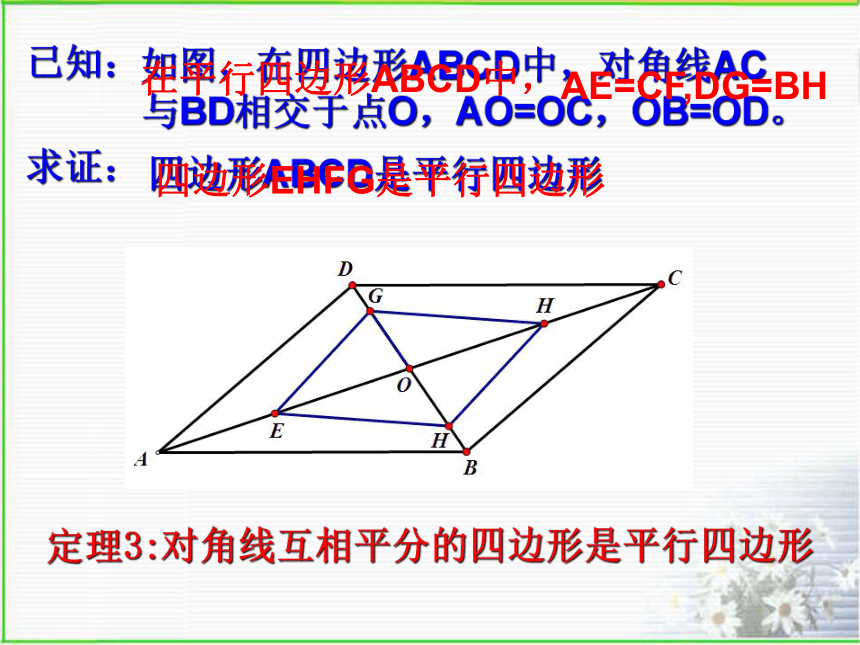
在平行四边形ABCD中，
AE=CF,DG=BH
四边形ABCD是平行四边形
四边形EHFG是平行四边形
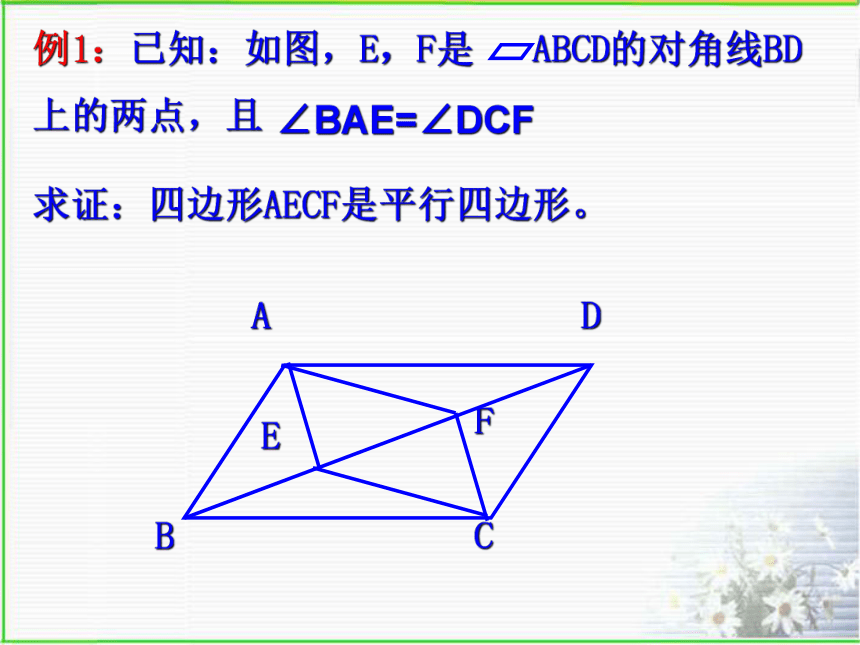
例1：已知：如图，E，F是 ABCD的对角线BD上的两点，且
求证：四边形AECF是平行四边形。
A
B
C
D
E
F
∠BAE=∠DCF
例1：已知：如图，E，F是 ABCD的对角线BD上的两点，且
求证：四边形AECF是平行四边形。
A
B
C
D
E
F
∠BAE=∠DCF
AE平分∠BAD,CF平分∠ BCD
变式:已知：如图,在 ABCD中，E,F是对角线BD上的两点,且BE=DF.M,N分别是AD和BC边上的中点. 求证：四边形ENFM是平行四边形。
A
B
C
D
E
F
M
N
探究活动
任意画一个三角形和三角形一边上的中线。比较这条中线的二倍与三角形另外两边的和的大小，你发现了什么 再画几个三角形试一试，你发现的规律仍然成立吗 试证明你的发现。
发现：三角形一条边上的中线的2倍小于另两条边的和。
E
已知：如图，AD是⊿ABC的中线，
求证：2AD证明：
如图，延长AD至E,使ED=AD.连结BE,EC.
∵BD=CD,
∴四边形ABEC是平行四边形（对角线互相平分的四边形是平行四边形）。
∴AB=CE(平行四边形的两组对边分别相等)。
∵AC+CE>AE,
∴AB+AC>2AD,
即2ADD
C
B
A
将中线延长一倍
例2：如图，在△ABC中，AB=14，BC=18，BO是AC边上的中线，求BO的取值范围。
O
A
B
C
说能出你这节课的收获和体验让大家与你分享吗？
平行四边形的性质定理和判定定理
条 件 结 论
性质
定理
判定
定理
1
四边形是平行四边形
两组对边平行且相等
四边形是平行四边形
对角线互相平分
2
1
2
3
四边形是平行四边形
四边形是平行四边形
四边形是平行四边形
两组对边分别相等
对角线互相平分
一组对边平行并且相等
性质：平行四边形的对角相等
定义：两组对边分别平行的四边形叫做平行四边形
平行四边形的两组对边分别平行