初中数学浙教版九年级上册第1章 二次函数二次函数复习课件(1)(共36张ppt)
文档属性
| 名称 | 初中数学浙教版九年级上册第1章 二次函数二次函数复习课件(1)(共36张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-01 18:24:59 | ||
图片预览





文档简介
(共36张PPT)
复习课(2)
二次函数y=x2-x-6的图象顶点坐标是__________
对称轴是_________。
(—,-
—)
1
25
2
4
直线x=—
1
2
一般式 y=ax?+bx+c
顶点式 y=a(x-m)?+k
二次函数的解析式:
(a≠0)
对称轴:直线x=m
顶点:(m,k)
二次函数的图象:
是一条抛物线
二次函数的图象的性质:
开口方向;
对称轴;
顶点坐标;
增减性;
最值
二次函数y=x2-x-6的图象顶点坐标是__________
对称轴是_________。
(—,
-
—
)
1
25
2
4
x=—
1
2
画二次函数的大致图象:
①画对称轴
②确定顶点
③确定与y轴的交点
④确定与x轴的交点
⑤确定与y轴交点关于对称轴对称的点
⑥连线
x=—
1
2
(—,-
—
)
1
25
2
4
(0,-6)
(-2,0)
(3,0)
0
x
y
(1,-6)
二次函数y=x2-x-6的图象顶点坐标是__________
对称轴是_________。
(—,-
—)
1
25
2
4
x=—
1
2
x=—
1
2
(—,-
—)
1
25
2
4
(0,-6)
(-2,0)
(3,0)
0
x
y
(1,-6)
增减性:
当
时,y随x的增大而减小
当
时,y随x的增大而增大
最值:
当
时,y有最
值,是
小
函数值y的正负性:
当
时,y>0
当
时,y=0
当
时,y<0
x<-2或x>3
x=-2或x=3
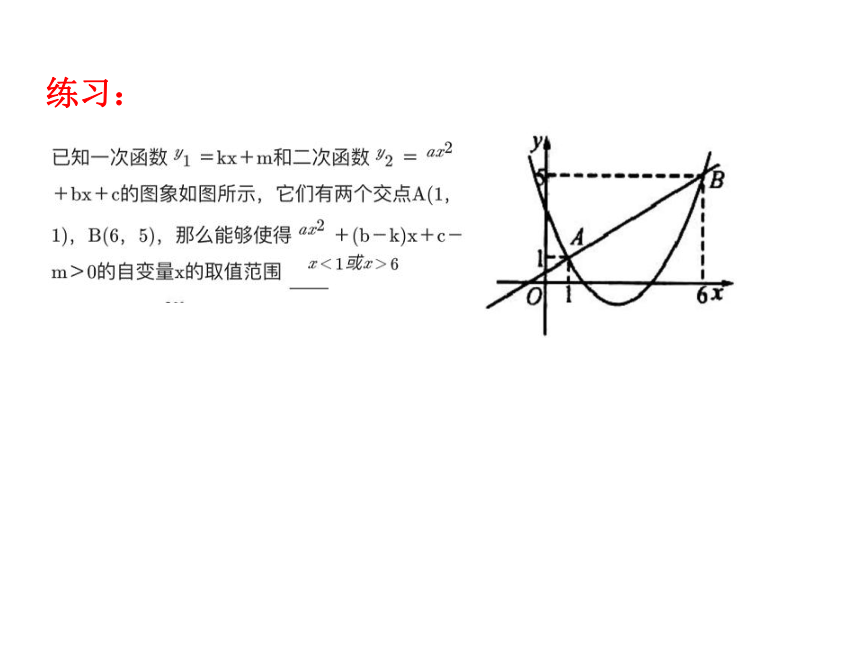
-2练习:
二次函数y=ax?+bx+c的图象如图所示,则在下列
各不等式中成立的个数是____________
1
-1
0
x
y
①abc<0
②a+b+c
<
0
③a+c
>
b
④2a+b=0
⑤
开口方向:向上a>0;向下a<0
对称轴:在y轴右侧a、b异号;
在y轴左侧a、b同号
与y轴的交点:在y轴正半轴c>0;在y轴负半轴c<0
与x轴的交点:两个不同b2-4ac>0;唯一b2-4ac=0;没有b2-4ac<0
a+b+c由当x=1时的点的位置决定;a-b+c由当x=-1时的点的位置决定
-2
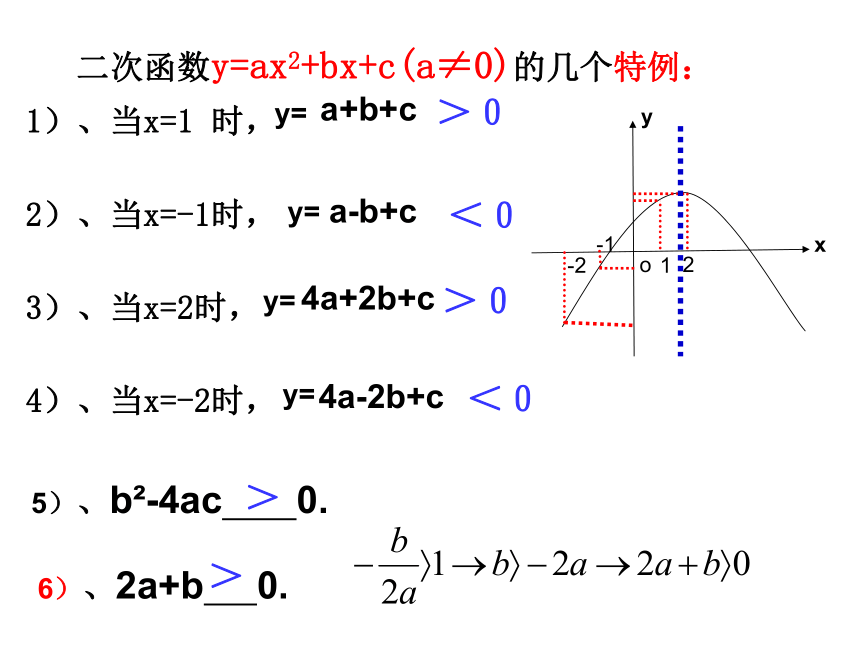
二次函数y=ax2+bx+c(a≠0)的几个特例:
1)、当x=1
时,
2)、当x=-1时,
3)、当x=2时,
4)、当x=-2时,
y=
y=
y=
y=
6)、2a+b
0.
x
y
o
1
-1
2
>0
<0
>0
<0
>
5)、b?-4ac
0.
>
a+b+c
a-b+c
4a+2b+c
4a-2b+c
y
=
ax2
y
=
ax2
+
k
y
=
a(x
–
m
)2
y
=
a(
x
–
m
)2
+
k
上下平移
左右平移
上下平移
左右平移
各种顶点式的二次函数的关系
左加右减上加下减
将
向左平移3个单位,再向下平移2个单位后,所得的抛物线的关系式是
(0,0)
(0,k)
(m,0)
(h,k)
抛物线
关于x轴对称的抛物线解析式是
解题思路:
①将原抛物线写成顶点式y=a(x-m)2+k
②写出顶点(m,k)
③写出顶点(m,k)关于x轴的点的坐标(m,-k)
则关于x轴对称的抛物线解析式是y=-a(x-m)2-k
关于x轴对称:
关于y轴对称:
①将原抛物线写成顶点式y=a(x-m)2+k
②写出顶点(m,k)
③写出顶点(m,k)关于y轴的点的坐标(-m,k)
则关于x轴对称的抛物线解析式是y=a(x+m)2+k
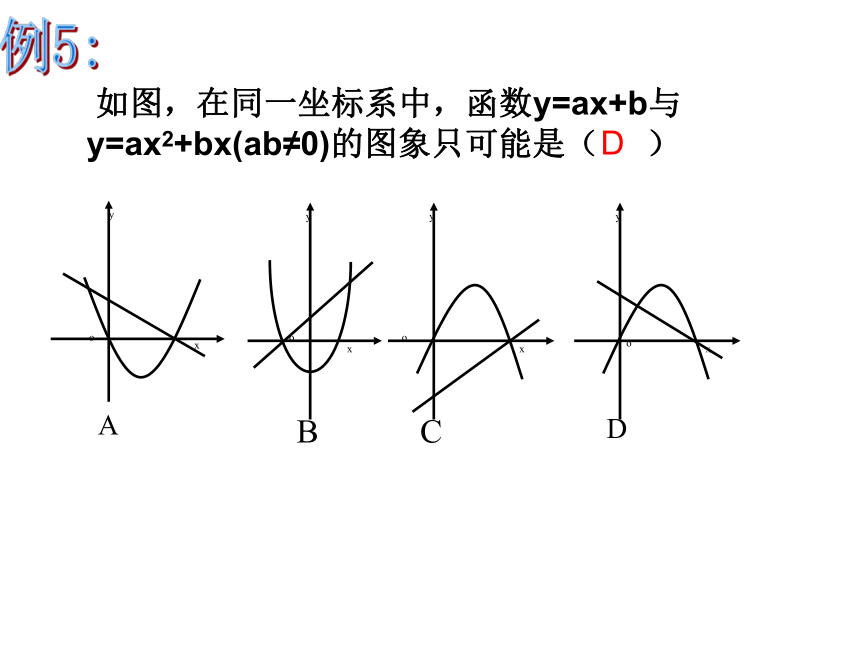
如图,在同一坐标系中,函数y=ax+b与
y=ax2+bx(ab≠0)的图象只可能是(
)
x
y
o
A
B
x
y
o
C
x
y
o
D
x
y
o
D
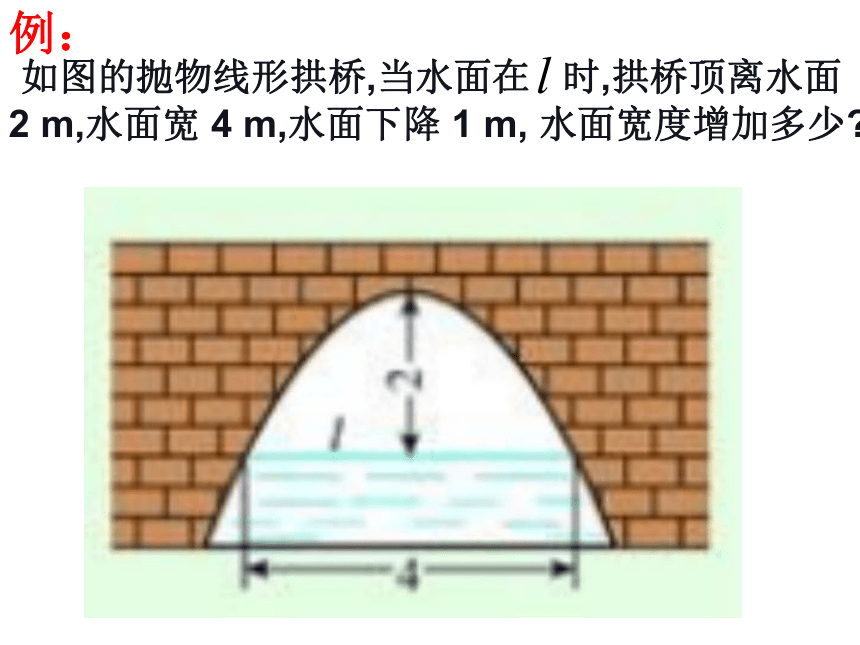
如图的抛物线形拱桥,当水面在
时,拱桥顶离水面
2
m,水面宽
4
m,水面下降
1
m,
水面宽度增加多少?
例:
X
y
x
y
0
0
注意:
在解决实际问题时,我们应建立简单方便的平面直角坐标系.
如图的抛物线形拱桥,当水面在
时,拱桥顶离水面
2
m,
水面宽
4
m,水面下降
1
m,
水面宽度增加多少?
某宾馆有50个房间供游客居住,当每个房间的定价为每天180元时,房间会全部住满。当每个房间每天的定价每增加10元时,就会有一个房间空闲。如果游客居住房间,宾馆需对每个房间每天支出20元的各种费用.房价定为多少时,宾馆利润最大?
解:设每个房间每天增加x元,宾馆的利润为y元
Y=(50-x/10)(180+x)-20(50-x/10)
Y=-1/10x?+34x+8000
1.有长24m的篱笆,一面利用围墙围城如图中间隔有一道篱笆的矩形花圃,设花圃的垂直于墙的一边长为x
m,面积是s
m2,则s与x的关系式是
_______
2.如图,铅球的出手点C距地面1米,出手后的运动路线是抛物线,出手后4秒钟达到最大高度3米,则铅球运行路线的解析式为_______
3.县九年级的一场篮球比赛中,如图队员甲正在投篮,已知球出手时离地面高
m,当球出手后水平距离
为4m时到达最大高度4m,设篮球运行的轨迹为抛物线,建立如图的平面直角坐标系,设篮球出手后离地的水平距离为xm,高度为ym,则y关于x的函数解析式是 _________ .
练习:
4.某商场购进一种单价为40元的篮球,如果以单价50元售出,那么每月可售出500个,根据销售经验,如果每提高1元,销售量相应减少10个。
(1)假设销售单价提高x元,那么销售每个篮球所获得的利润是
元;这种篮球每月的销售量是
个(用含的代数式表示)。
(2)8000元是否为每月销售这种篮球的最大利润?如果是,请说明理由;如果不是,
请你求出最大利润,此时篮球的售价应定为多少元?
5.某瓜果基地市场部为指导该基地某种蔬菜的生产和销售,在对历年市场行情和生产的情况进行调查的基础上.对今年这种蔬菜上市后的市场售价和生产成本进行了预测,得到了以下图象:
每千克售价(元)
月
3
6
3
5
0
请你根据图象提供的信息说明:
(1)在3月份出售这种蔬菜,每千克的收益是多少?(收益=售价-成本)
(2)哪个月出售这种蔬菜,每千克的收益最大?请说明理由.
每千克成本(元)
月
3
6
1
4
0
课前热身
(1)直线
x
=
1,P(1,4)
(2)
A(-1,0)
B(3,0)
C(0,3)
(3)
8
已知二次函数
的图象与
x
轴交
于A、B两点,与
y
轴交于C点,顶点为P点.
(1)求出抛物线的对称轴和顶点坐标;
(-1,0)
(3,0)
(1,4)
(0,3)
A
C
P
B
E
o
(2)求出A、B、C的坐标;
(3)求△
PAB的面积.
二次函数中的重要点和重要线段
(1)重要的点
?顶点P
?与x轴的交点A(x1,0),B(x2,0)
?与y轴交点C
(0,C)
4
3
2
1
2
O
A
C
P
B
x
y
考点梳理
二次函数中的重要点和重要线段
(2)重要线段
?线段OC
?线段OA
、OB
?线段AB
?垂线段PH
?垂线段PE
4
3
2
1
2
O
A
C
P
B
x
y
H
E
考点梳理
x1
x2
解析式
点的坐标
线段长
面积
典例解析:已知抛物线y=-x2+2x+3与x轴交于A,B两点,其中A点位于B点的左侧,与y轴交于C点,顶点为P,
S△
AOC=______________
S△
BOC=_______
4
3
2
1
2
O
A
C
P
B
(0,3)
(-1,0)
(3,0)
(1,4)
x
y
S△
COP=_______
S△
PAB=_______
4
3
2
1
2
O
A
C
P
B
(0,3)
(-1,0)
(3,0)
(1,4)
8
x
y
D
E
一边在坐标轴上的三角形
S△
PCB=_______
(3,0)
4
3
2
1
2
O
A
C
P
B
(0,3)
(-1,0)
(1,4)
E
3
y
补形
(0,4)
三边都不在坐标轴上的三角形
S△
PCB=_______
(3,0)
4
3
2
1
2
O
A
C
P
B
(0,3)
(-1,0)
(1,4)
3
y
D
分割
y=-x+3
(1,2)
E
F
三边都不在坐标轴上的三角形
(3,0)
4
3
2
1
2
O
A
C
P
B
(0,3)
(-1,0)
(1,4)
(t,-t2+2t+3)
(t,-t+3)
H
M
y
x
例2设直线x=t(0交于点H,与直线BC交于点M.
(1)用t表示点H,点M的坐标,线段HM的长度.
x=t
能力提升
y=-x+3
(3,0)
4
3
2
1
2
O
A
C
P
B
(0,3)
(-1,0)
(1,4)
(t,-t2+2t+3)
(t,-t+3)
H
M
y
x
E
F
(2)写出△BCH的面积与t的关系式?
x=t
(3)当t为何值时,△BCH的面积最大?
并求出最大值.
【思维模式】:求面积最值的一般方法是建立图形面积和某个变量之间的函数关系式,然后根据函数的性质以及自变量的取值范围进行确定.
(3,0)
4
3
2
1
2
O
A
C
P
B
(0,3)
(-1,0)
(1,4)
变式:H为直线BC上方在抛物线
上的动点,求△BCH面积的
最大值
H
y
x
(3,0)
4
3
2
1
2
O
A
C
P
B
(0,3)
(-1,0)
(1,4)
变式:H为直线BC上方在抛物线
上的动点,求△BCH面积的
最大值
H
y
x
动中取静,静中求动
x=t
M
(3,0)
4
3
2
1
2
O
A
C
P
B
(0,3)
(-1,0)
(1,4)
变式:H为直线BC上方在抛物线
上的动点,求△BCH面积的
最大值
H
y
x
动中取静,静中求动
E
(t,-t2+2t+3)
二次函数的综合应用
1
、如图①,
已知抛物线
y=ax?+bx+3
(a≠0)与
x轴交于点A(1,0)和点B
(-3,0),与y轴交于点C.
(1)
求抛物线的解析式;
(2)在(1)中抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出Q点的坐标;若不存在,请说明理由.
(3)
设抛物线的对称轴与
x轴交于点M,
问在对称轴上是否存在点P,使△CMP为等腰三角形?若存在,请直接写出所有符合条件的点P的坐标;若不存在,请说明理由.
(4)
如图②,若点E为第二象限抛物线上一动点,连接BE、CE,求四边形BOCE面积的最大值,并求此时E点的坐标.
1.如图①,
已知抛物线y=ax?+bx+3
(a≠0)与
x轴交于点A(1,0)和点B
(-3,0),与y轴交于点C.
(1)
求抛物线的解析式;
(2)在(1)中抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出Q点的坐标;若不存在,请说明理由.
Q
(1,0)
(-3,0)
(0,3)
y=-x?-2x+3
Q(-1,2)
(3)
设抛物线的对称轴与
x轴交于点M
,问在对称轴上是否存在点P,使△CMP为等腰三角形?若存在,请直接写出所有符合条件的点P的坐标;若不存在,请说明理由.
?以M为圆心,MC为半径画弧,与对称轴有两交点;以C为圆心,MC为半径画弧,与对称轴有一个交点(MC为腰)。
?作MC的垂直平分线与对称轴有一个交点(MC为底边)。
(1,0)
(-3,0)
(0,3)
(-1,0)
(4)
如图②,若点E为第二象限抛物线上一动点,连接BE、CE,求四边形BOCE面积的最大值,并求此时E点的坐标.
E
F
(1,0)
(0,3)
(-3,0)
(m,-m?-2m+3
)
复习课(2)
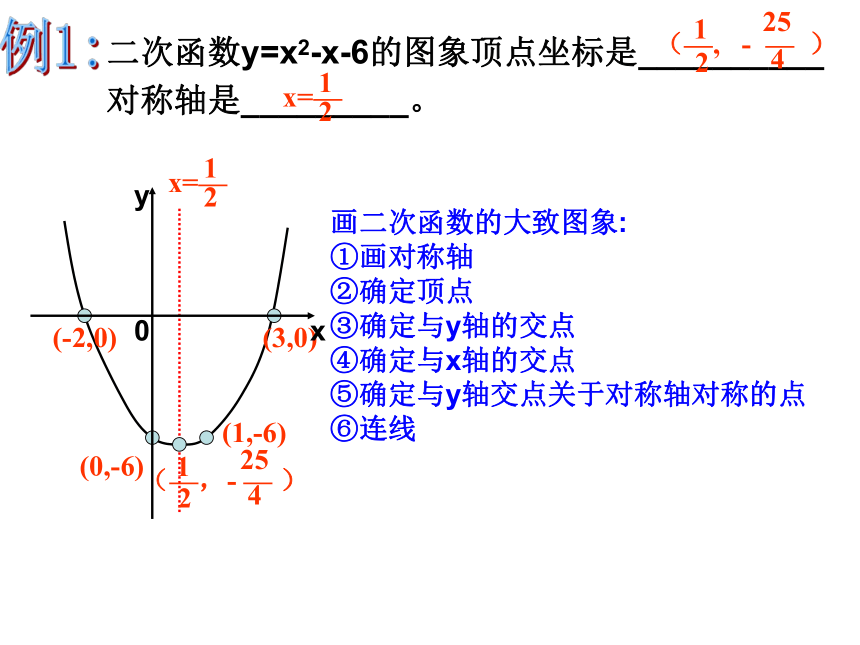
二次函数y=x2-x-6的图象顶点坐标是__________
对称轴是_________。
(—,-
—)
1
25
2
4
直线x=—
1
2
一般式 y=ax?+bx+c
顶点式 y=a(x-m)?+k
二次函数的解析式:
(a≠0)
对称轴:直线x=m
顶点:(m,k)
二次函数的图象:
是一条抛物线
二次函数的图象的性质:
开口方向;
对称轴;
顶点坐标;
增减性;
最值
二次函数y=x2-x-6的图象顶点坐标是__________
对称轴是_________。
(—,
-
—
)
1
25
2
4
x=—
1
2
画二次函数的大致图象:
①画对称轴
②确定顶点
③确定与y轴的交点
④确定与x轴的交点
⑤确定与y轴交点关于对称轴对称的点
⑥连线
x=—
1
2
(—,-
—
)
1
25
2
4
(0,-6)
(-2,0)
(3,0)
0
x
y
(1,-6)
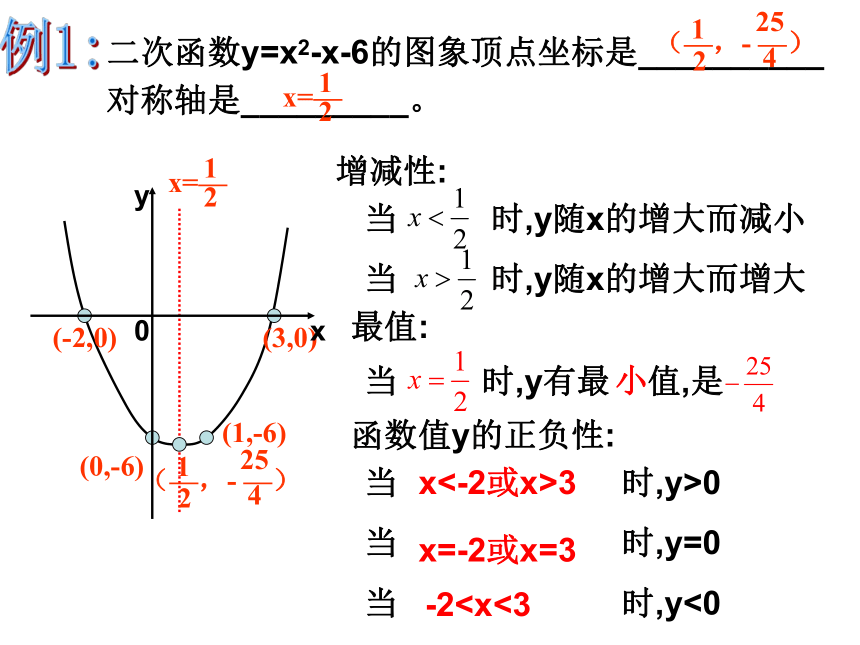
二次函数y=x2-x-6的图象顶点坐标是__________
对称轴是_________。
(—,-
—)
1
25
2
4
x=—
1
2
x=—
1
2
(—,-
—)
1
25
2
4
(0,-6)
(-2,0)
(3,0)
0
x
y
(1,-6)
增减性:
当
时,y随x的增大而减小
当
时,y随x的增大而增大
最值:
当
时,y有最
值,是
小
函数值y的正负性:
当
时,y>0
当
时,y=0
当
时,y<0
x<-2或x>3
x=-2或x=3
-2
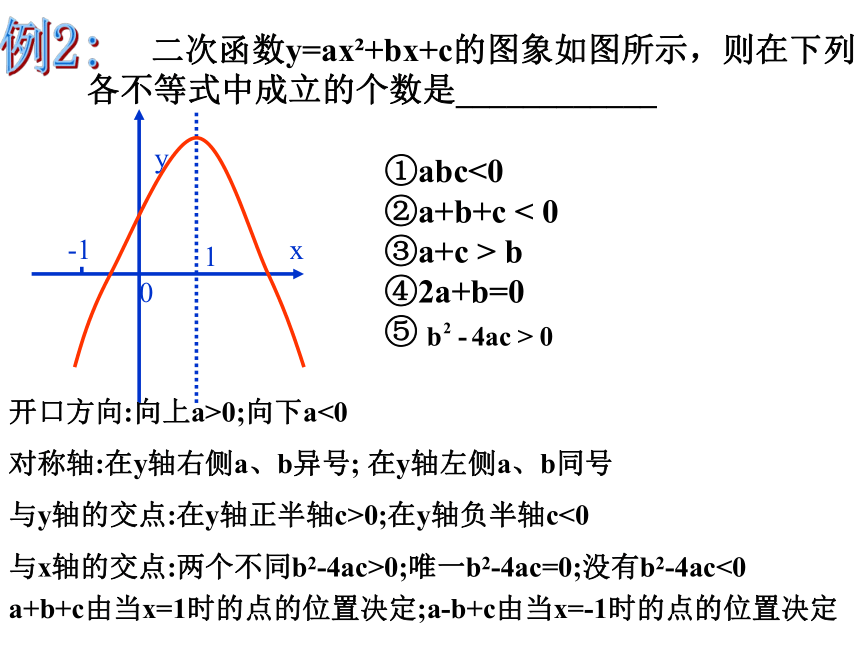
二次函数y=ax?+bx+c的图象如图所示,则在下列
各不等式中成立的个数是____________
1
-1
0
x
y
①abc<0
②a+b+c
<
0
③a+c
>
b
④2a+b=0
⑤
开口方向:向上a>0;向下a<0
对称轴:在y轴右侧a、b异号;
在y轴左侧a、b同号
与y轴的交点:在y轴正半轴c>0;在y轴负半轴c<0
与x轴的交点:两个不同b2-4ac>0;唯一b2-4ac=0;没有b2-4ac<0
a+b+c由当x=1时的点的位置决定;a-b+c由当x=-1时的点的位置决定
-2
二次函数y=ax2+bx+c(a≠0)的几个特例:
1)、当x=1
时,
2)、当x=-1时,
3)、当x=2时,
4)、当x=-2时,
y=
y=
y=
y=
6)、2a+b
0.
x
y
o
1
-1
2
>0
<0
>0
<0
>
5)、b?-4ac
0.
>
a+b+c
a-b+c
4a+2b+c
4a-2b+c
y
=
ax2
y
=
ax2
+
k
y
=
a(x
–
m
)2
y
=
a(
x
–
m
)2
+
k
上下平移
左右平移
上下平移
左右平移
各种顶点式的二次函数的关系
左加右减上加下减
将
向左平移3个单位,再向下平移2个单位后,所得的抛物线的关系式是
(0,0)
(0,k)
(m,0)
(h,k)
抛物线
关于x轴对称的抛物线解析式是
解题思路:
①将原抛物线写成顶点式y=a(x-m)2+k
②写出顶点(m,k)
③写出顶点(m,k)关于x轴的点的坐标(m,-k)
则关于x轴对称的抛物线解析式是y=-a(x-m)2-k
关于x轴对称:
关于y轴对称:
①将原抛物线写成顶点式y=a(x-m)2+k
②写出顶点(m,k)
③写出顶点(m,k)关于y轴的点的坐标(-m,k)
则关于x轴对称的抛物线解析式是y=a(x+m)2+k
如图,在同一坐标系中,函数y=ax+b与
y=ax2+bx(ab≠0)的图象只可能是(
)
x
y
o
A
B
x
y
o
C
x
y
o
D
x
y
o
D
如图的抛物线形拱桥,当水面在
时,拱桥顶离水面
2
m,水面宽
4
m,水面下降
1
m,
水面宽度增加多少?
例:
X
y
x
y
0
0
注意:
在解决实际问题时,我们应建立简单方便的平面直角坐标系.
如图的抛物线形拱桥,当水面在
时,拱桥顶离水面
2
m,
水面宽
4
m,水面下降
1
m,
水面宽度增加多少?
某宾馆有50个房间供游客居住,当每个房间的定价为每天180元时,房间会全部住满。当每个房间每天的定价每增加10元时,就会有一个房间空闲。如果游客居住房间,宾馆需对每个房间每天支出20元的各种费用.房价定为多少时,宾馆利润最大?
解:设每个房间每天增加x元,宾馆的利润为y元
Y=(50-x/10)(180+x)-20(50-x/10)
Y=-1/10x?+34x+8000
1.有长24m的篱笆,一面利用围墙围城如图中间隔有一道篱笆的矩形花圃,设花圃的垂直于墙的一边长为x
m,面积是s
m2,则s与x的关系式是
_______
2.如图,铅球的出手点C距地面1米,出手后的运动路线是抛物线,出手后4秒钟达到最大高度3米,则铅球运行路线的解析式为_______
3.县九年级的一场篮球比赛中,如图队员甲正在投篮,已知球出手时离地面高
m,当球出手后水平距离
为4m时到达最大高度4m,设篮球运行的轨迹为抛物线,建立如图的平面直角坐标系,设篮球出手后离地的水平距离为xm,高度为ym,则y关于x的函数解析式是 _________ .
练习:
4.某商场购进一种单价为40元的篮球,如果以单价50元售出,那么每月可售出500个,根据销售经验,如果每提高1元,销售量相应减少10个。
(1)假设销售单价提高x元,那么销售每个篮球所获得的利润是
元;这种篮球每月的销售量是
个(用含的代数式表示)。
(2)8000元是否为每月销售这种篮球的最大利润?如果是,请说明理由;如果不是,
请你求出最大利润,此时篮球的售价应定为多少元?
5.某瓜果基地市场部为指导该基地某种蔬菜的生产和销售,在对历年市场行情和生产的情况进行调查的基础上.对今年这种蔬菜上市后的市场售价和生产成本进行了预测,得到了以下图象:
每千克售价(元)
月
3
6
3
5
0
请你根据图象提供的信息说明:
(1)在3月份出售这种蔬菜,每千克的收益是多少?(收益=售价-成本)
(2)哪个月出售这种蔬菜,每千克的收益最大?请说明理由.
每千克成本(元)
月
3
6
1
4
0
课前热身
(1)直线
x
=
1,P(1,4)
(2)
A(-1,0)
B(3,0)
C(0,3)
(3)
8
已知二次函数
的图象与
x
轴交
于A、B两点,与
y
轴交于C点,顶点为P点.
(1)求出抛物线的对称轴和顶点坐标;
(-1,0)
(3,0)
(1,4)
(0,3)
A
C
P
B
E
o
(2)求出A、B、C的坐标;
(3)求△
PAB的面积.
二次函数中的重要点和重要线段
(1)重要的点
?顶点P
?与x轴的交点A(x1,0),B(x2,0)
?与y轴交点C
(0,C)
4
3
2
1
2
O
A
C
P
B
x
y
考点梳理
二次函数中的重要点和重要线段
(2)重要线段
?线段OC
?线段OA
、OB
?线段AB
?垂线段PH
?垂线段PE
4
3
2
1
2
O
A
C
P
B
x
y
H
E
考点梳理
x1
x2
解析式
点的坐标
线段长
面积
典例解析:已知抛物线y=-x2+2x+3与x轴交于A,B两点,其中A点位于B点的左侧,与y轴交于C点,顶点为P,
S△
AOC=______________
S△
BOC=_______
4
3
2
1
2
O
A
C
P
B
(0,3)
(-1,0)
(3,0)
(1,4)
x
y
S△
COP=_______
S△
PAB=_______
4
3
2
1
2
O
A
C
P
B
(0,3)
(-1,0)
(3,0)
(1,4)
8
x
y
D
E
一边在坐标轴上的三角形
S△
PCB=_______
(3,0)
4
3
2
1
2
O
A
C
P
B
(0,3)
(-1,0)
(1,4)
E
3
y
补形
(0,4)
三边都不在坐标轴上的三角形
S△
PCB=_______
(3,0)
4
3
2
1
2
O
A
C
P
B
(0,3)
(-1,0)
(1,4)
3
y
D
分割
y=-x+3
(1,2)
E
F
三边都不在坐标轴上的三角形
(3,0)
4
3
2
1
2
O
A
C
P
B
(0,3)
(-1,0)
(1,4)
(t,-t2+2t+3)
(t,-t+3)
H
M
y
x
例2设直线x=t(0
(1)用t表示点H,点M的坐标,线段HM的长度.
x=t
能力提升
y=-x+3
(3,0)
4
3
2
1
2
O
A
C
P
B
(0,3)
(-1,0)
(1,4)
(t,-t2+2t+3)
(t,-t+3)
H
M
y
x
E
F
(2)写出△BCH的面积与t的关系式?
x=t
(3)当t为何值时,△BCH的面积最大?
并求出最大值.
【思维模式】:求面积最值的一般方法是建立图形面积和某个变量之间的函数关系式,然后根据函数的性质以及自变量的取值范围进行确定.
(3,0)
4
3
2
1
2
O
A
C
P
B
(0,3)
(-1,0)
(1,4)
变式:H为直线BC上方在抛物线
上的动点,求△BCH面积的
最大值
H
y
x
(3,0)
4
3
2
1
2
O
A
C
P
B
(0,3)
(-1,0)
(1,4)
变式:H为直线BC上方在抛物线
上的动点,求△BCH面积的
最大值
H
y
x
动中取静,静中求动
x=t
M
(3,0)
4
3
2
1
2
O
A
C
P
B
(0,3)
(-1,0)
(1,4)
变式:H为直线BC上方在抛物线
上的动点,求△BCH面积的
最大值
H
y
x
动中取静,静中求动
E
(t,-t2+2t+3)
二次函数的综合应用
1
、如图①,
已知抛物线
y=ax?+bx+3
(a≠0)与
x轴交于点A(1,0)和点B
(-3,0),与y轴交于点C.
(1)
求抛物线的解析式;
(2)在(1)中抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出Q点的坐标;若不存在,请说明理由.
(3)
设抛物线的对称轴与
x轴交于点M,
问在对称轴上是否存在点P,使△CMP为等腰三角形?若存在,请直接写出所有符合条件的点P的坐标;若不存在,请说明理由.
(4)
如图②,若点E为第二象限抛物线上一动点,连接BE、CE,求四边形BOCE面积的最大值,并求此时E点的坐标.
1.如图①,
已知抛物线y=ax?+bx+3
(a≠0)与
x轴交于点A(1,0)和点B
(-3,0),与y轴交于点C.
(1)
求抛物线的解析式;
(2)在(1)中抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出Q点的坐标;若不存在,请说明理由.
Q
(1,0)
(-3,0)
(0,3)
y=-x?-2x+3
Q(-1,2)
(3)
设抛物线的对称轴与
x轴交于点M
,问在对称轴上是否存在点P,使△CMP为等腰三角形?若存在,请直接写出所有符合条件的点P的坐标;若不存在,请说明理由.
?以M为圆心,MC为半径画弧,与对称轴有两交点;以C为圆心,MC为半径画弧,与对称轴有一个交点(MC为腰)。
?作MC的垂直平分线与对称轴有一个交点(MC为底边)。
(1,0)
(-3,0)
(0,3)
(-1,0)
(4)
如图②,若点E为第二象限抛物线上一动点,连接BE、CE,求四边形BOCE面积的最大值,并求此时E点的坐标.
E
F
(1,0)
(0,3)
(-3,0)
(m,-m?-2m+3
)
同课章节目录
